「
「
「数学基础
」
」
」第
3
3
3章 同余问题
目录:
A.同余方程
B.约数之和
C.线性求逆元
D.中国剩余定理
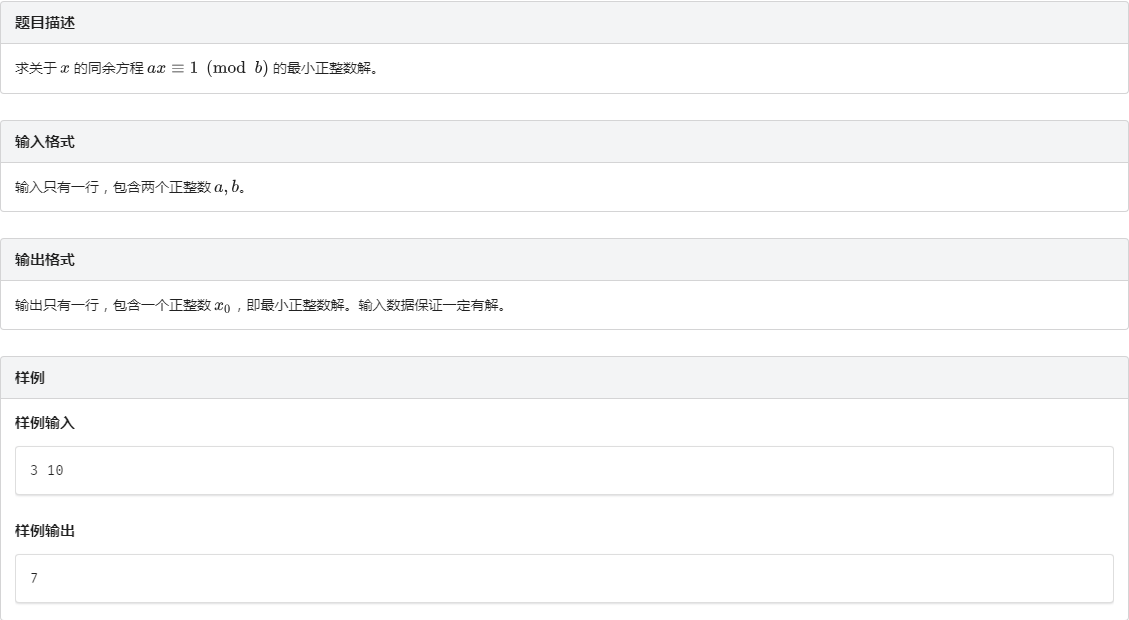
A . A. A. 例题 1 1 1 同余方程
洛谷
l
i
n
k
link
link
分析:
拓展欧几里得
(
e
x
g
c
d
)
(exgcd)
(exgcd) 板子
由于要求最小正整数解 最后要对答案进行处理
CODE:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
ll a,b,x,y;
void exgcd(ll a,ll b)
{
if(b==0)
{
x=1;
y=0;
return;
}
exgcd(b,a%b);
ll k=x;
x=y;
y=k-a/b*y;
}
int main()
{
scanf("%lld%lld",&a,&b);
exgcd(a,b);
printf("%lld",(x%b+b)%b);
return 0;
}
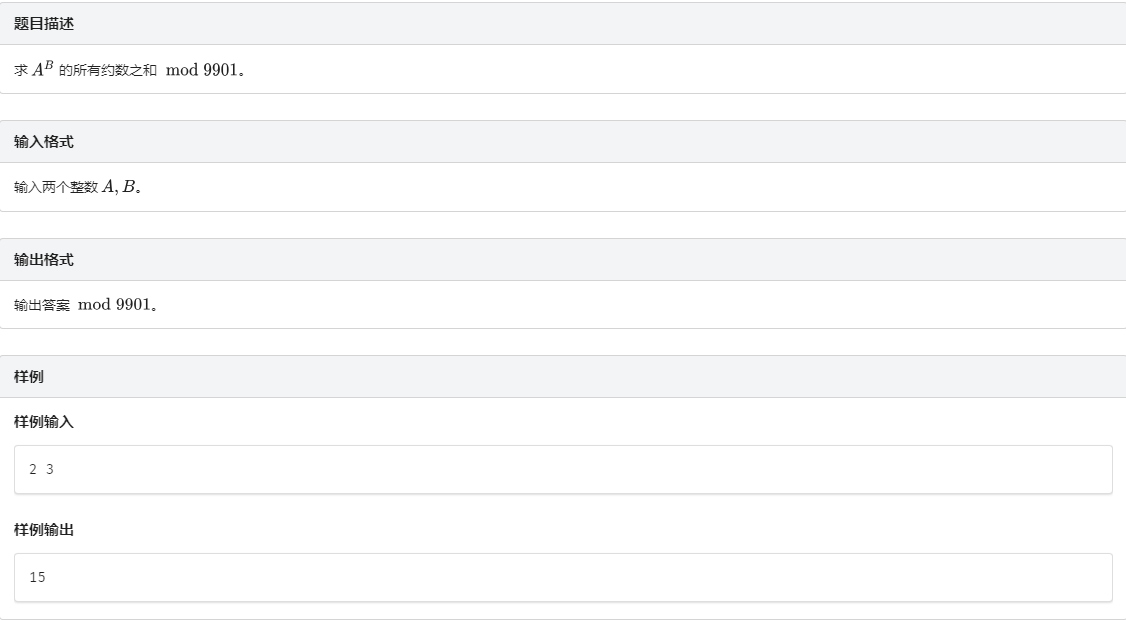
B . B. B. 例题 2 2 2 约数之和
分析:
唯一分解定理:
A
=
p
1
k
1
×
p
2
k
2
×
.
.
.
×
p
n
k
n
A=p_1^{k_1}times p_2^{k_2}times...times p_n^{k_n}
A=p1k1×p2k2×...×pnkn
那么
A
B
=
p
1
k
1
×
B
×
p
2
k
2
×
B
×
.
.
.
×
p
n
k
n
×
B
A^B=p_1^{k_1times B}times p_2^{k_2times B}times...times p_n^{k_ntimes B}
AB=p1k1×B×p2k2×B×...×pnkn×B
A
B
A^B
AB的约数和为
∏
i
=
1
n
(
∑
j
=
0
B
×
k
i
p
i
j
)
∏_{i=1}^n(sum_{j=0}^{Btimes k_i}p_i^j)
∏i=1n(∑j=0B×kipij)
然后等比数列求和
∏
i
=
1
n
(
p
i
B
×
k
i
+
1
−
1
p
i
−
1
)
∏_{i=1}^n(frac{p_i^{Btimes k_i+1}-1}{p_i-1})
∏i=1n(pi−1piB×ki+1−1)
分子可以用快速幂求出 分母看是否与
9901
9901
9901互质 不互质就是
p
i
−
1
p_i-1
pi−1的乘法逆元
如果互质 则
p
i
p_i
pi
m
o
d
mod
mod
9901
=
1
9901=1
9901=1 该项变为
i
∑
j
=
0
k
j
×
B
=
k
i
×
B
+
1
i^{sum_{j=0}^{k_jtimes B}}=k_itimes B+1
i∑j=0kj×B=ki×B+1
m
o
d
mod
mod
9901
9901
9901
CODE:
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<iostream>
using namespace std;
typedef long long ll;
const int Mod=9901;
ll prime[105],c[105],ans=1ll,A,B,tot;
void Div(int x) //分解质因子
{
for(int i=2;i*i<=x;i++)
{
if(x%i==0) prime[++tot]=i;
while(x%i==0)
{
c[tot]++;
x/=i;
}
}
if(x>1)
{
prime[++tot]=x;
c[tot]=1;
}
}
ll ksm(ll a,ll k)
{
ll res=1;
while(k)
{
if(k&1) (res*=a)%=Mod;
k>>=1;
(a*=a)%=Mod;
}
return res;
}
int main()
{
scanf("%lld%lld",&A,&B);
Div(A);
for(int i=1;i<=tot;i++)
{
if((prime[i]-1)%Mod==0)
{
ans=ans*(B*c[i]+1)%Mod;
continue;
}
int tmp=ksm(prime[i],B*c[i]+1);
tmp=(tmp-1+Mod)%Mod;
int inv=prime[i]-1;
inv=ksm(inv,Mod-2); //逆元
ans=ans%Mod*inv*tmp%Mod;
}
printf("%lld",ans);
return 0;
}
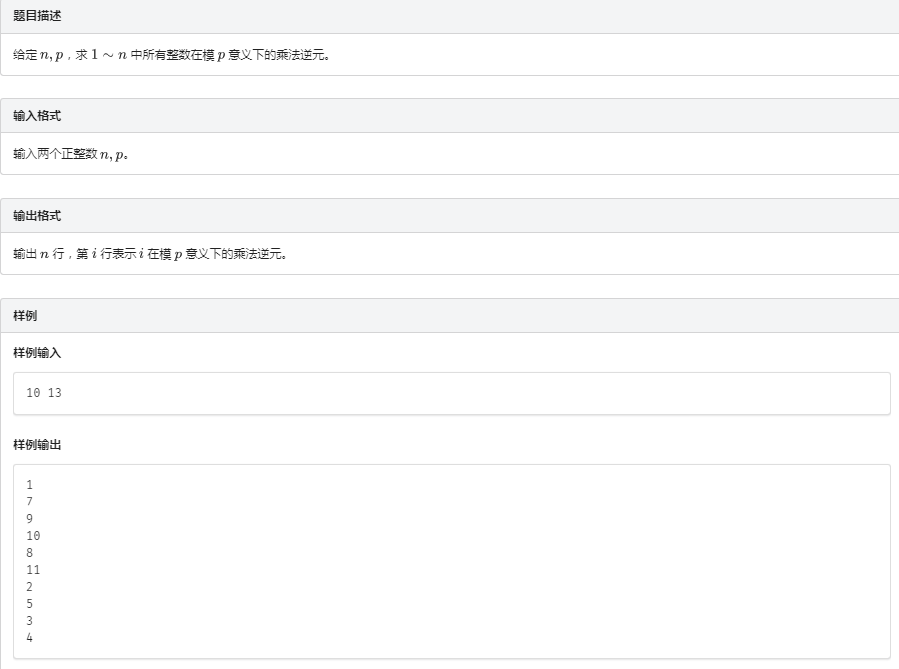
C . C. C. 例题 3 3 3 线性求逆元
洛谷
l
i
n
k
link
link
分析:
逆元线性递推公式 模板
CODE:
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<iostream>
using namespace std;
typedef long long ll;
const int N=3e6+5;
int n,p,inv[N];
int main()
{
scanf("%d%d",&n,&p);
inv[1]=1;
for(int i=2;i<=n;i++)
inv[i]=(ll)(p-p/i)*inv[p%i]%p;
for(int i=1;i<=n;i++)
printf("%dn",inv[i]);
return 0;
}
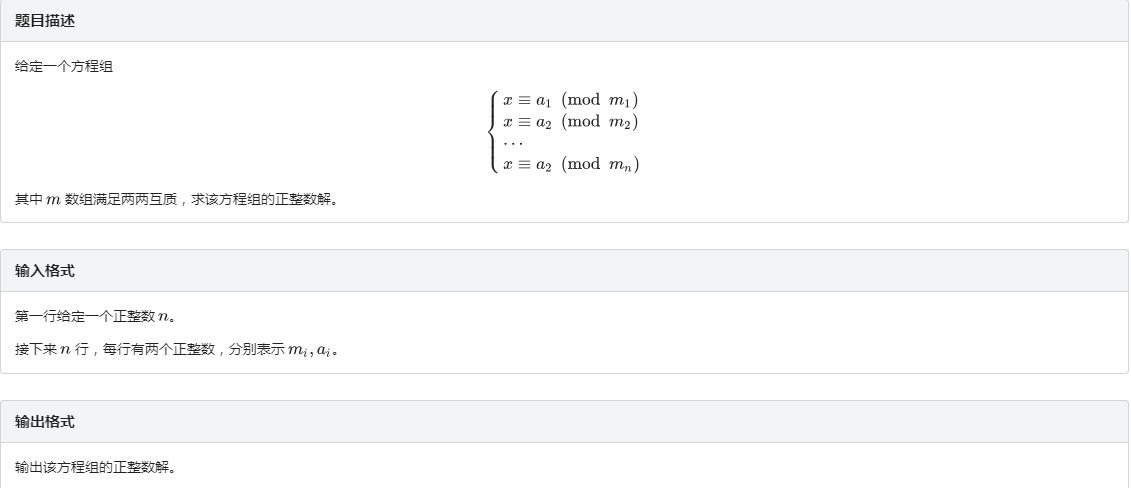
D . D. D. 例题 4 4 4 中国剩余定理
洛谷
l
i
n
k
link
link
分析:
e
x
g
c
d
+
C
R
T
exgcd+CRT
exgcd+CRT 板子
注意处理负数的
CODE:
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<iostream>
using namespace std;
typedef long long ll;
ll n,a[16],b[16],Mod=1,ans;
void exgcd(ll a,ll b,ll &x,ll &y)
{
if(!b){
x=1;
y=0;
return;
}
exgcd(b,a%b,x,y);
int k=x;
x=y;
y=k-a/b*y;
}
int main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld%lld",&a[i],&b[i]);
Mod*=a[i];
}
for(int i=1;i<=n;i++) //求方程组数
{
ll x=0,y=0;
exgcd(Mod/a[i],a[i],x,y);
(ans+=b[i]*Mod/a[i]%Mod*(x<0?x+a[i]:x))%=Mod;
}
printf("%lld",ans%Mod);
return 0;
}
最后
以上就是彩色汉堡最近收集整理的关于【Ybt OJ】[数学基础 第3章] 同余问题分析:分析:分析:分析:的全部内容,更多相关【Ybt内容请搜索靠谱客的其他文章。




![【Ybt OJ】[数学基础 第3章] 同余问题分析:分析:分析:分析:](https://www.shuijiaxian.com/files_image/reation/bcimg1.png)

![[YBtOJ]最多约数](https://www.shuijiaxian.com/files_image/reation/bcimg3.png)

发表评论 取消回复