洗牌算法shuffle

将原来数组的数组进行打散，使原数组的某个数在打散后的数组中的每个位置上等概率的出现。

很容易想到，需要用到随机数函数，而且应该是一个平均分布的随机数函数，还需要一个不放回的采样的生成模式。

（1）random.seed([x])
伪随机数生成模块。如果不提供 seed，默认使用系统时间。使用相同的 seed，可以获得完全相同的随机数序列，常用于算法改进测试。

>>>from random import *
>>>a = Random(); a.seed(1)
>>>[a.randint(1, 100) for i in range(20)]
[14, 85, 77, 26, 50, 45, 66, 79, 10, 3, 84, 44, 77, 1, 45, 73, 23, 95, 91, 4]

>>>b = Random(); b.seed(1)
>>>[b.randint(1, 100) for i in range(20)]
[14, 85, 77, 26, 50, 45, 66, 79, 10, 3, 84, 44, 77, 1, 45, 73, 23, 95, 91, 4]

(2)random.random
用于生成一个0到1的随机符点数: 0 <= n < 1.0

(3)random.randint
用于生成一个指定范围内的整数。其中参数a是下限，参数b是上限，生成的随机数n: a <= n <= b

(4)random.randrange
从指定范围内，按指定基数递增的集合中 获取一个随机数。如：random.randrange(10, 100, 2)，结果相当于从[10, 12, 14, 16, … 96, 98]序列中获取一个随机数。

这里２、３、４的分布默认都是平均分布。

关于python 内置数据结构算法时间复杂度

Fisher–Yates Shuffle(时间复杂度：O(n²))

算法思想就是从 原始数组中随机抽取一个新的数字到新数组中 。算法英文描述如下：

• Write down the numbers from 1 through N.
• Pick a random number k between one and the number of unstruck numbers remaining (inclusive).
• Counting from the low end, strike out the kth number not yet struck out, and write it down elsewhere.
• Repeat from step 2 until all the numbers have been struck out.
• The sequence of numbers written down in step 3 is now a random permutation of the original numbers.

python实现代码：

#Fisher–Yates Shuffle
'''
 1. 从还没处理的数组（假如还剩k个）中，随机产生一个[0, k]之间的数字p（假设数组从0开始）；
 2. 从剩下的k个数中把第p个数取出；
 3. 重复步骤2和3直到数字全部取完；
 4. 从步骤3取出的数字序列便是一个打乱了的数列。
'''
import random

def shuffle(lis):
  result = []
  while lis:
    p = random.randrange(0, len(lis))
    result.append(lis[p])
    lis.pop(p)#时间复杂度(O(n))
  return result

r = shuffle([1, 2, 2, 3, 3, 4, 5, 10])
print(r)

Knuth-Durstenfeld Shuffle(时间复杂度：O(n))

Knuth 和Durstenfeld 在Fisher 等人的基础上对算法进行了改进。 每次从未处理的数据中随机取出一个数字，然后把该数字放在数组的尾部，即数组尾部存放的是已经处理过的数字 。这是一个原地打乱顺序的算法，算法时间复杂度也从Fisher算法的 O(n²)提升到了O(n)。算法 伪代码如下：

#Knuth-Durstenfeld Shuffle
def shuffle(lis):
  for i in range(len(lis) - 1, 0, -1):
    p = random.randrange(0, i + 1)
    lis[i], lis[p] = lis[p], lis[i]
  return lis

r = shuffle([1, 2, 2, 3, 3, 4, 5, 10])
print(r)

Inside-Out Algorithm(时间复杂度：O(n))

Knuth-Durstenfeld Shuffle 是一个in-place算法，原始数据被直接打乱，有些应用中可能需要保留原始数据，因此需要开辟一个新数组来存储打乱后的序列。 Inside-Out Algorithm 算法的基本思想是设一游标i从前向后扫描原始数据的拷贝，在[0, i]之间随机一个下标j，然后用位置j的元素替换掉位置i的数字，再用原始数据位置i的元素替换掉拷贝数据位置j的元素。其作用相当于在拷贝数据中交换i与j位置处的值。

#Inside-Out Algorithm
def shuffle(lis):
  result = lis[:]
  for i in range(1, len(lis)):
    j = random.randrange(0, i)
    result[i] = result[j]
    result[j] = lis[i]
  return result

r = shuffle([1, 2, 2, 3, 3, 4, 5, 10])
print(r)

小节：

其实python自己就有一个shuffle函数：

import random
r = [1, 2, 2, 3, 3, 4, 5, 10]
random.shuffle(r)
print r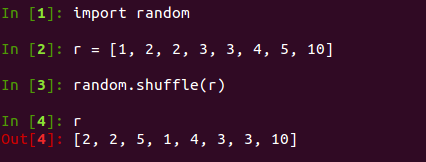

我们可以看到这是一个原地打乱算法。

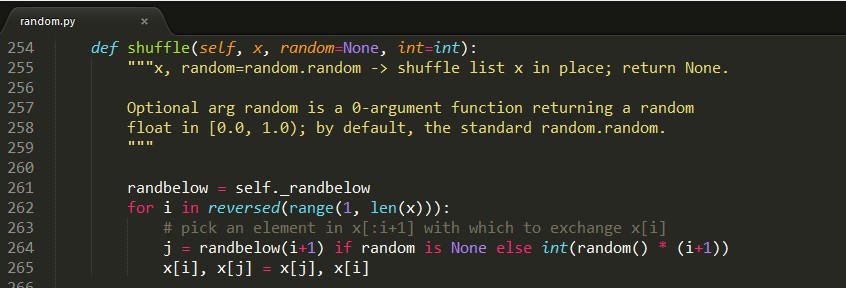
从shuffle内部的实现我们也能看到，这里使用的是Knuth-Durstenfeld Shuffle算法

转载自：http://www.tuicool.com/articles/qIjqQzb

最后

以上就是拼搏荔枝为你收集整理的洗牌算法shuffle的全部内容，希望文章能够帮你解决洗牌算法shuffle所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。