我是靠谱客的博主 霸气汉堡，最近开发中收集的这篇文章主要介绍【C++】[STL]----map和set一、map的应用二、set的应用三、红黑树的封装四、map和set的模拟实现，觉得挺不错的，现在分享给大家，希望可以做个参考。
概述
map和set是STL容器中的部分，这篇文章讲解map和set的应用以及底层原理。
一、map的应用
1.1 map文档介绍
map是存储由键值和映射值的组合形成的元素的关联容器，遵循特定的顺序。
map中数据建立映射关系：
typedef pair<const Key, T> value_type;map中的元素总是按照其内部比较对象指示的特定严格弱排序标准按其键排序。
map容器通过键访问单个元素的速度通常比无序映射容器慢，但它们允许基于其顺序对子集进行直接迭代。
map中的映射值可以通过使用括号运算符的相应键直接访问。
1.2 STL库中map的功能
1.2.1 迭代器
1.2.2 容量
1.2.3 元素访问
1.2.4 修改器
1.2.5 操作
1.2.6 空间配置器
1.3 map的使用
void TestMap()
{
map<string, string> m;
// 向map中插入元素的方式：
// 将键值对<"peach","桃子">插入map中，用pair直接来构造键值对
m.insert(pair<string, string>("peach", "桃子"));
// 将键值对<"peach","桃子">插入map中，用make_pair函数来构造键值对
m.insert(make_pair("banan", "香蕉"));
// 借用operator[]向map中插入元素
/*operator[]的原理是：
用<key, T()>构造一个键值对，然后调用insert()函数将该键值对插入到map中
如果key已经存在，插入失败，insert函数返回该key所在位置的迭代器
如果key不存在，插入成功，insert函数返回新插入元素所在位置的迭代器
operator[]函数最后将insert返回值键值对中的value返回*/
// 将<"apple", "">插入map中，插入成功，返回value的引用，将“苹果”赋值给该引用结果，
m["apple"] = "苹果";
// key不存在时抛异常
//m.at("waterme") = "水蜜桃";
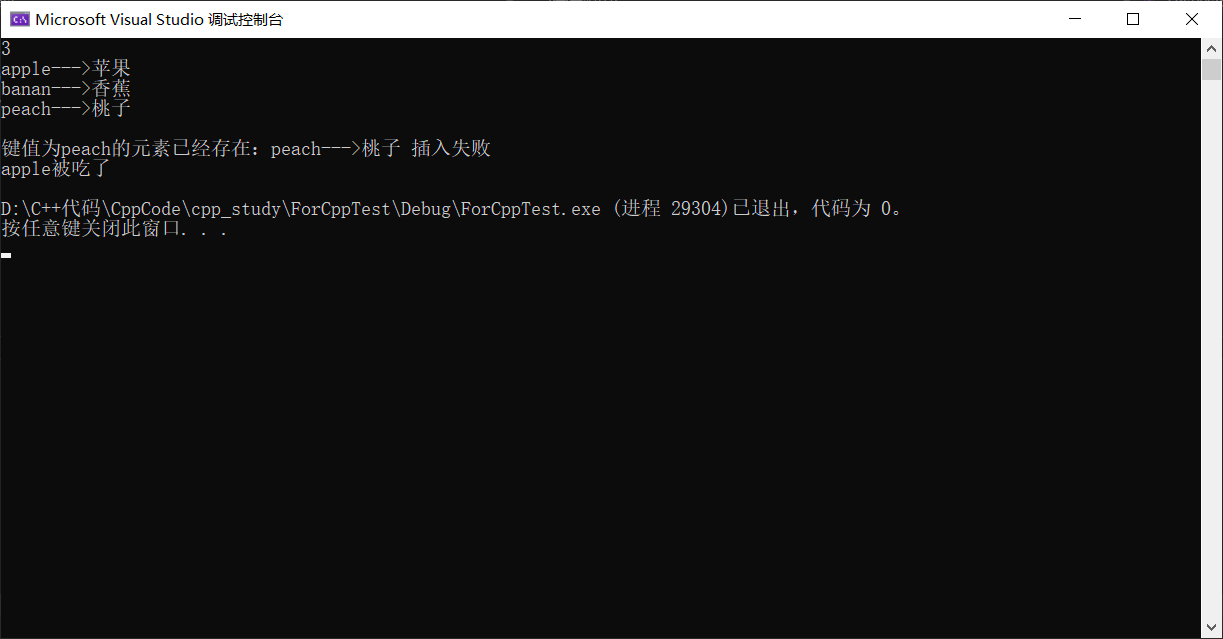
cout << m.size() << endl;
// 用迭代器去遍历map中的元素，可以得到一个按照key排序的序列
for (auto& e : m)
cout << e.first << "--->" << e.second << endl;
cout << endl;
// map中的键值对key一定是唯一的，如果key存在将插入失败
auto ret = m.insert(make_pair("peach", "桃色"));
if (ret.second)
cout << "<peach, 桃色>不在map中, 已经插入" << endl;
else
cout << "键值为peach的元素已经存在：" << ret.first->first << "--->"
<< ret.first->second << " 插入失败" << endl;
// 删除key为"apple"的元素
m.erase("apple");
if (1 == m.count("apple"))
cout << "apple还在" << endl;
else
cout << "apple被吃了" << endl;
}
二、set的应用
2.1 set的文档介绍
set是按照特定顺序存储唯一元素的容器。
在set中，元素的值也标识它（值本身是T类型的键），并且每个值都必须是唯一的。set中元素的值不能在容器中修改一次（元素总是常量），但可以从容器中插入或删除它们。
2.2 STL中set的功能
2.2.1 迭代器
2.2.2 容量
2.2.3 修改器
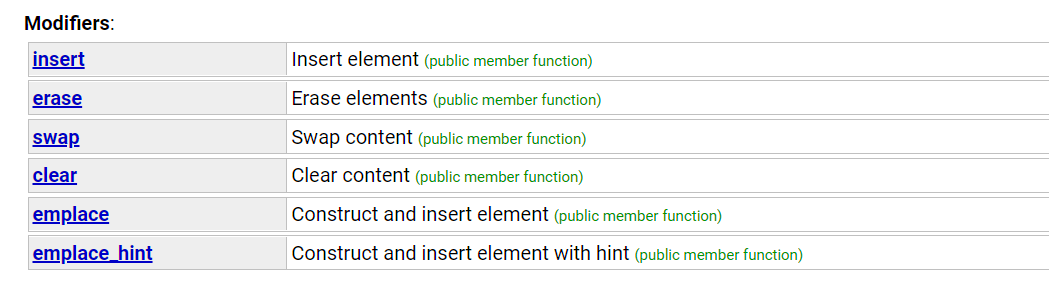
2.2.4 操作
2.2.5 空间配置器
2.3 set的使用
void TestSet()
{
// 用数组array中的元素构造set
int array[] = { 1, 3, 5, 7, 9, 2, 4, 6, 8, 0, 1, 3, 5, 7, 9, 2, 4,6, 8, 0 };
set<int> s(array, array + sizeof(array) / sizeof(array));
cout << s.size() << endl;
// 正向打印set中的元素，从打印结果中可以看出：set可去重
for (auto& e : s)
{
cout << e << " ";
}
cout << endl;
// 使用迭代器逆向打印set中的元素
for (auto it = s.rbegin(); it != s.rend(); ++it)
{
cout << *it << " ";
}
cout << endl;
// set中值为3的元素出现了几次
cout << s.count(3) << endl;
}
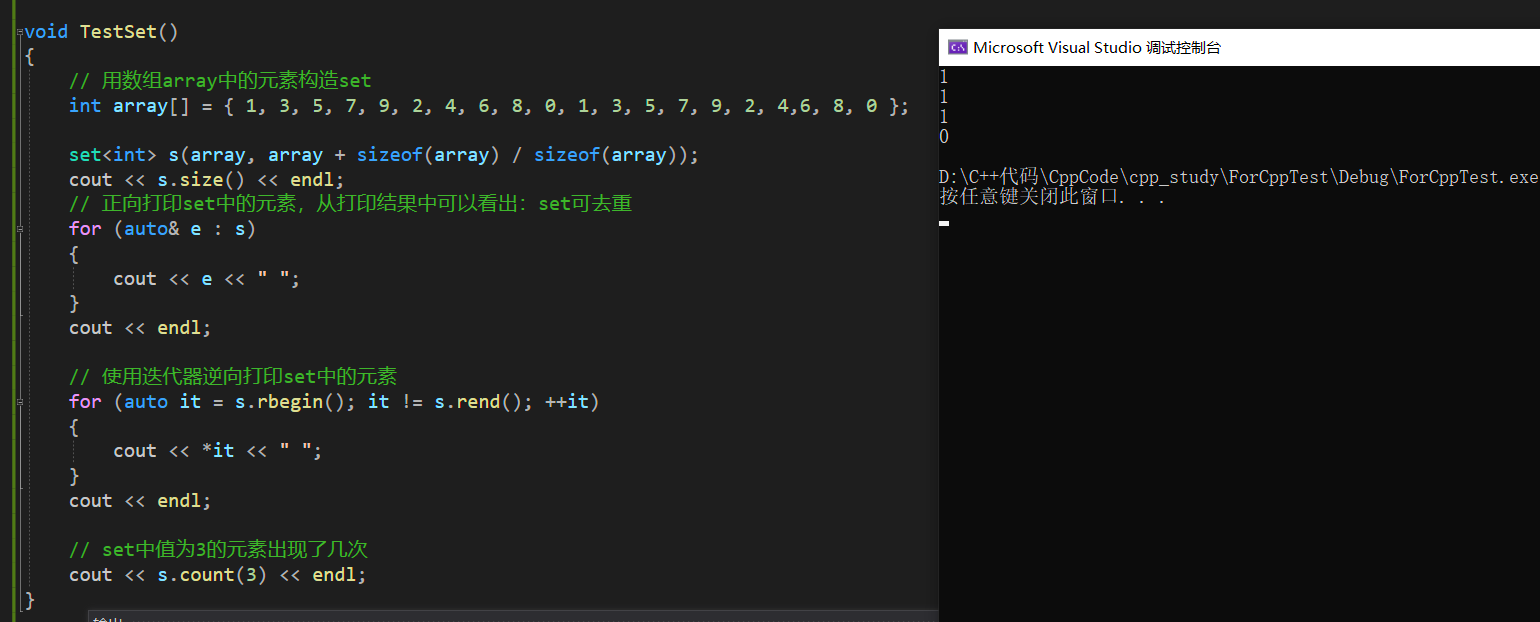
三、红黑树的封装
map 和 set的底层都是用红黑树实现的。
map 和 set中的接口都是复用红黑树的接口，可以封装红黑树从而封装出map和set。
由于map的数据是pair<K, V>类型的，set是T单参数类型的，首先对红黑树的节点进行变化，再依次进行下去。
3.1 红黑树的节点
T也可以是pair<K, V>类型
enum Colour
{
RED,
BLACK
};
// 节点
template <class T>
struct RBTreeNode
{
RBTreeNode<T>* _parent;
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
T _data;
Colour _col;
RBTreeNode(const T& data)
: _parent(nullptr)
, _left(nullptr)
, _right(nullptr)
, _data(data)
{}
};3.2 红黑树的迭代器
begin()是树的最左节点，end()是树的最右节点。
++begin就是找下一个比该节点大的节点
operator++
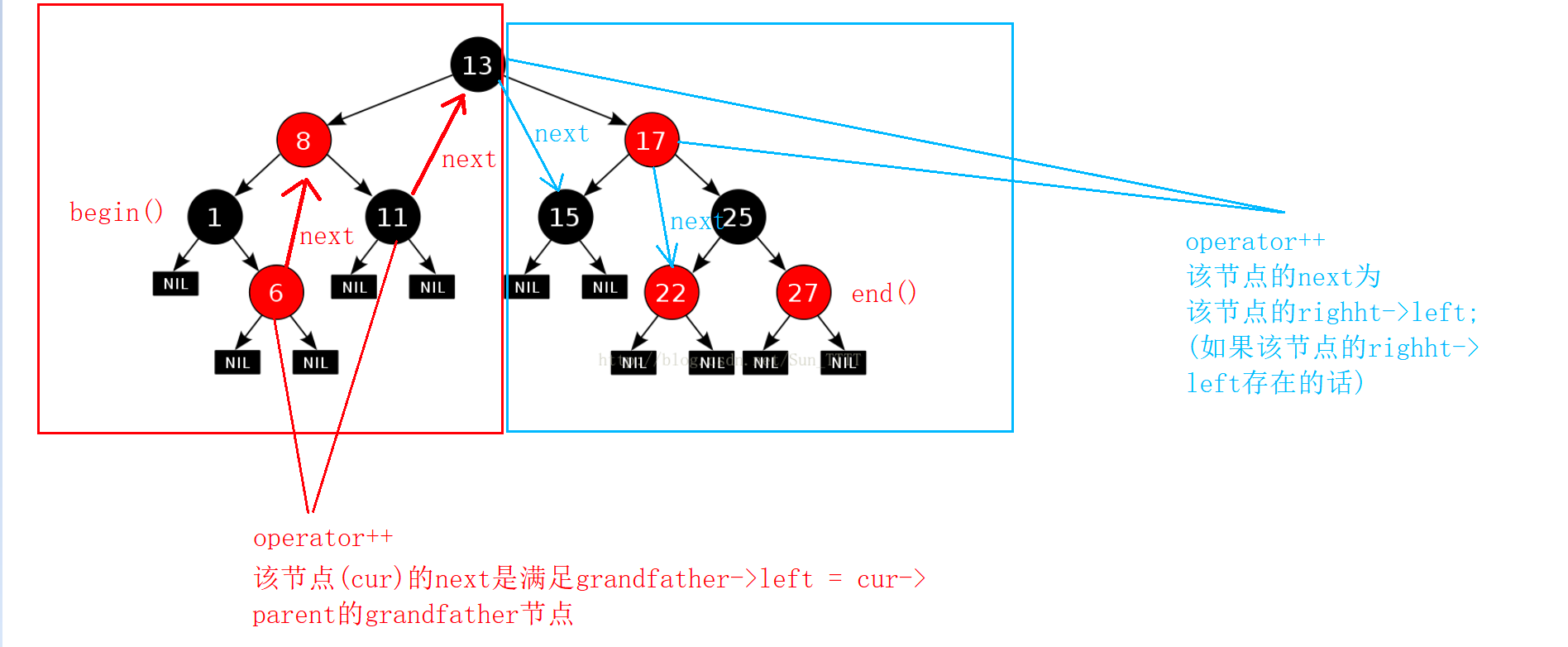
operator-- 类似
Self& operator++()
{
if (_node->_right)
{
// 下一个就是右树的最左节点
Node* left = _node->_right;
while (left->_left)
{
left = left->_left;
}
_node = left;
}
else
{
// 找祖先不是更上面祖先的右的那个祖先
Node* parent = _node->_parent;
Node* cur = _node;
while (parent && cur == parent->_right)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self& operator--()
{
if (_node->_left)
{
// 下一个是左子树的最右节点
Node* right = _node->_left;
while (right->_right)
{
right = right->_right;
}
}
else
{
// 找祖先不是更上面祖先的左的那个祖先
Node* parent = _node->_parent;
Node* cur = _node;
while (parent && cur == parent->_left)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}3.3 改造红黑树
因为关联式容器中存储的是<key, value>的键值对，因此
k为key的类型，
ValueType: 如果是map，则为pair<K, V>; 如果是set，则为k
KeyOfValue: 通过value来获取key的一个仿函数类
完整代码：
#pragma once
enum Colour
{
RED,
BLACK
};
// 节点
template <class T>
struct RBTreeNode
{
RBTreeNode<T>* _parent;
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
T _data;
Colour _col;
RBTreeNode(const T& data)
: _parent(nullptr)
, _left(nullptr)
, _right(nullptr)
, _data(data)
{}
};
template<class T, class Ref, class Ptr>
struct __RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef __RBTreeIterator<T, Ref, Ptr> Self;
Node* _node;
__RBTreeIterator(Node* node)
: _node(node)
{}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &_node->_data;
}
bool operator!=(const Self& s) const
{
return _node != s._node;
}
bool operator==(const Self& s) const
{
return _node = s._node;
}
Self& operator++()
{
if (_node->_right)
{
// 下一个就是右树的最左节点
Node* left = _node->_right;
while (left->_left)
{
left = left->_left;
}
_node = left;
}
else
{
// 找祖先不是更上面祖先的右的那个祖先
Node* parent = _node->_parent;
Node* cur = _node;
while (parent && cur == parent->_right)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self& operator--()
{
if (_node->_left)
{
// 下一个是左子树的最右节点
Node* right = _node->_left;
while (right->_right)
{
right = right->_right;
}
}
else
{
// 找祖先不是更上面祖先的左的那个祖先
Node* parent = _node->_parent;
Node* cur = _node;
while (parent && cur == parent->_left)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
};
// 红黑树
template<class K, class T, class KeyOfT>
struct RBTree
{
typedef RBTreeNode<T> Node;
public:
typedef __RBTreeIterator<T, T&, T*> iterator;
iterator begin()
{
Node* left = _root;
while (left && left->_left)
{
left = left->_left;
}
return iterator(left);
}
iterator end()
{
return iterator(nullptr);
}
pair<iterator, bool> Insert(const T& data)
{
KeyOfT kot;
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return make_pair(iterator(_root), true);
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else if (kot(cur->_data) < kot(data))
{
parent = cur;
cur = cur->_right;
}
else
{
return make_pair(iterator(cur), false);
}
}
cur = new Node(data);
Node* newnode = cur;
cur->_col = RED;
if (kot(cur->_data) < kot(data))
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
assert(grandfather || grandfather->_col == BLACK);
// 通过uncle分出不同情况
if (parent == grandfather->_left)
{
Node* uncle = grandfather->_right;
// 情况一 parent uncle都存在且都为红
// 变色处理
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
//情况二+三 parent存在且为红，uncle存在且为黑 parent存在 unlce不存在
else
{
if (cur == parent->_left)
{
// 情况二
// 右单旋+变色
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
// 情况三
// 左右单旋+变色
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else
{
Node* uncle = grandfather->_left;
// 情况一 parent uncle都存在且都为红
// 变色处理
if (uncle && uncle->_col == RED)
{
grandfather->_col = RED;
parent->_col = BLACK;
uncle->_col = BLACK;
cur = grandfather;
parent = cur->_parent;
}
//情况二+三 parent存在且为红，uncle存在且为黑 parent存在 unlce不存在
else
{
if (cur == parent->_right)
{
// 情况二
// 左单旋+变色
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
// 情况三
// 右左单旋+变色
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return make_pair(iterator(newnode), true);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool IsBalance()
{
if (_root == nullptr)
{
return true;
}
if (_root->_col == RED)
{
cout << "根节点不是黑色！！！" << endl;
return false;
}
// 黑色节点基准值
int benchmark = 0;
return _PrevCheck(_root, 0, benchmark);
}
private:
// 中序遍历
void _InOrder(const Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << kot(_root->_data) << endl;
_InOrder(root->_right);
}
// 检查
bool _PrevCheck(Node* root, int blacknum, int& benchmark)
{
if (root == nullptr)
{
if (benchmark == 0)
{
benchmark = blacknum;
return true;
}
if (blacknum != benchmark) // 某条路径上黑色节点数目不一样
{
cout << "某条路径上黑色节点数目不一样" << endl;
return false;
}
else
{
return true;
}
}
if (root->_col = BLACK)
{
++blacknum;
}
if (root->_col == RED && root->_parent->_col == RED)
{
cout << "存在连续的红色节点！！！" << endl;
return false;
}
return _PrevCheck(root->_left, blacknum, benchmark)
&& _PrevCheck(root->_right, blacknum, benchmark);
}
// 功能函数
//1、左单旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
Node* ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (_root == parent)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
}
// 2、右单旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
Node* ppNode = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (_root == parent)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
}
private:
Node* _root = nullptr;
};四、map和set的模拟实现
通过上文对红黑树的改造，我们可以通过红黑树的相关接口封装map和set。
4.1 map的模拟实现
#pragma once
#include"RedBlack.h"
namespace Abert
{
template<class K, class V>
class map
{
struct MapKeyOfT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
public:
typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator;
iterator begin()
{
return _m.begin();
}
iterator end()
{
return _m.end();
}
pair<iterator, bool> Insert(const pair<K, V>& kv)
{
return _m.Insert(kv);
}
V& operator[](const K& key)
{
pair<iterator, bool> ret = Insert(make_pair(key, V()));
return ret.first->second;
}
private:
RBTree<K, pair<K, V>, MapKeyOfT> _m;
};
// 测试map
void test_map()
{
string arr[] = { "靓仔", "西瓜", "苹果", "西瓜", "苹果", "靓仔", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
map<string, int> countMap;
for (auto& str : arr)
{
// 1、str不在countMap中，插入pair(str, int()),然后在对返回次数++
// 2、str在countMap中，返回value(次数)的引用，次数++;
countMap[str]++;
}
map<string, int>::iterator it = countMap.begin();
while (it != countMap.end())
{
cout << it->first << ":" << it->second << endl;
++it;
}
/*for (auto& kv : countMap)
{
cout << kv.first << ":" << kv.second << endl;
}*/
}
}4.2 set的模拟实现
#pragma once
#include"RedBlack.h"
namespace Abert
{
template<class K>
class set
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator;
iterator begin()
{
return _s.begin();
}
iterator end()
{
return _s.end();
}
pair<iterator, bool> Insert(const K& key)
{
return _s.Insert(key);
}
private:
RBTree<K, K, SetKeyOfT> _s;
};
// 测试set
void test_set()
{
set<int> s;
set<int>::iterator it = s.begin();
while (it != s.end())
{
cout << *it << " ";
++it;
}
cout << endl;
s.Insert(3);
s.Insert(2);
s.Insert(1);
s.Insert(5);
s.Insert(3);
s.Insert(6);
s.Insert(4);
s.Insert(9);
s.Insert(7);
it = s.begin();
while (it != s.end())
{
cout << *it << " ";
++it;
}
cout << endl;
}
}以上就是本文的全部内容，欢迎大家交流。
最后
以上就是霸气汉堡为你收集整理的【C++】[STL]----map和set一、map的应用二、set的应用三、红黑树的封装四、map和set的模拟实现的全部内容，希望文章能够帮你解决【C++】[STL]----map和set一、map的应用二、set的应用三、红黑树的封装四、map和set的模拟实现所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
![【C++】[STL]----map和set一、map的应用二、set的应用三、红黑树的封装四、map和set的模拟实现](/uploads/reation/bcimg7.png)
发表评论 取消回复