Q学习例子

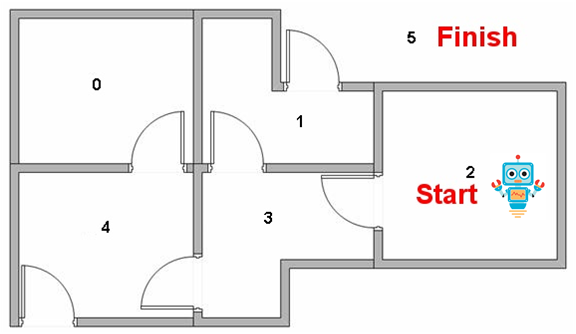
假设建筑物中有5个房间，如上图所示。我们将每个房间的编号设为0到4.建筑物的外部可以被认为是一个大房间（5）。当然，5号房间的回报率为100，其他所有与目标房间的直接连接奖励为100。

Q（1,5）= R（1,5）+ 0.8 * Max [] = 100 + 0.8 * 0 = 100

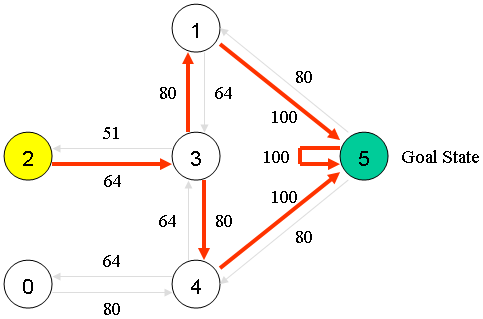
机器人从状态2开始，我们希望他能够学习到房子外面状态5。

状态列表：
状态0可到达——>状态4；
状态1可到达——>状态3、5；
状态2可到达——>状态3；
状态3可到达——>状态1、2、4；
状态4可到达——>状态0、3、5；
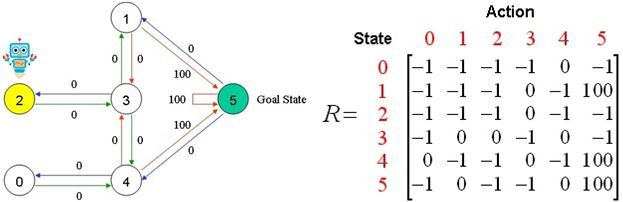
状态5可到达——>状态1、4、5；

我们可以将状态图和即时奖励值放入以下奖励表格“矩阵R”中。

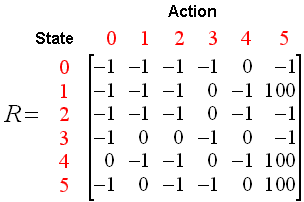
R-table

其中：[-1]表示状态之间是不互通；[0]表示状态之间互通，奖励为0；[100]表示状态之间互通，奖励为100。

R矩阵的列是机器人所处状态X_{0、1、2、3、4、5}下一步能到达的房间状态的可能。

R矩阵的行是能到达状态X_{0、1、2、3、4、5}机器人所处的房间状态。

例如：第一列是指状态0，下一步可到达的房间状态4；（参见上面的状态列表）

第一行是指下一步到达房间状态0，只有状态4；（参见上面的状态列表）

现在我们添加一个类似“矩阵R”的“矩阵Q”作为Agent的大脑，即通过经验学到的东西。“矩阵Q”的行表示Agent当前的状态，列表示下一个状态（节点之间的链接）的可能动作。

Agent开始什么都不知道，“矩阵Q”被初始化为零。“矩阵Q”只能从一个元素开始。如果找到新状态，则更新“矩阵Q”，这被称为无监督学习。

Q-table

Q-learning的过渡规则是一个非常简单的公式：

Q（状态，动作）= R（状态，动作）+ Gamma *最大[ Q（下一个状态，所有动作）]
即：Q(state, action) = R(state, action) + Gamma * Max[Q(next state, all actions)]

根据该公式，分配给矩阵Q的特定元素的值等于矩阵R中的对应值与学习参数Gamma之和，乘以下一状态下所有可能动作的Q的最大值。

举例说明：【将学习参数Gamma设置为0.8】

First：随机选择初始状态1

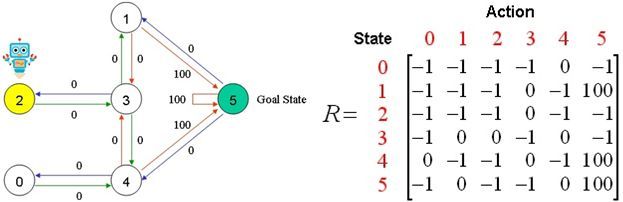
第一步：在R-table的第二列（状态1）下一跳能到达状态3、5；

第二步：随机选择下一跳，假设为状态5；

第三步：计算Q-table，更新，，因为5是目标状态，所以我们完成了一轮；

Q（状态，动作）= R（状态，动作）+ Gamma *max[ Q（下一个状态，所有动作）]
Q（1,5）= R（1,5）+ 0.8 * Max [ Q（5，1），Q（5，4），（5，5）] = 100 + 0.8 * 0 = 100

update Q-table

First round：update Q-table

Second ：随机选择初始状态3

第一步：在R-table的第四列（状态3）下一跳能到达状态1、2、4；

第二步：随机选择下一跳，假设为状态1；

第三步：在R-table的第二列（状态1）下一跳能到达状态3、5；

第四步：计算Q-table，更新，，

Q（状态，动作）= R（状态，动作）+ Gamma *max[ Q（下一个状态，所有动作）]
Q（3,1）= R（3,1）+ 0.8 * Max [ Q（1,3），Q（1,5）] = 0 + 0.8 * Max（0,100）= 80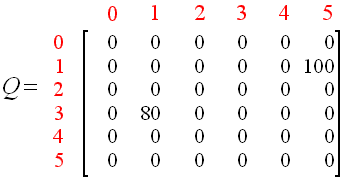

Third 随机选择初始状态4

第一步：在R-table的第五列（状态4）下一跳能到达状态0、3、5；

第二步：随机选择下一跳，假设为状态5；

第三步：计算Q-table，更新，，因为5是目标状态，所以我们完成了一轮；

Q（状态，动作）= R（状态，动作）+ Gamma *max[ Q（下一个状态，所有动作）]
Q（4,5）= R（4,5）+ 0.8 * Max [Q（5，1），Q（5，4），（5，5）] = 100 + 0.8 * 0 = 100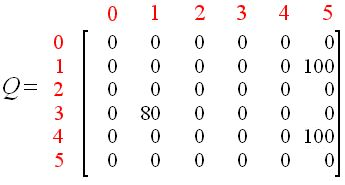

Four round：随机选择初始状态0

第一步：在R-table的第一列（状态0）下一跳能到达状态4；

第二步：只能选择下一跳，状态4；

第三步：在R-table的第五列（状态4）下一跳能到达状态3、5；

第四步：计算Q-table，更新，

Q（状态，动作）= R（状态，动作）+ Gamma *max[ Q（下一个状态，所有动作）]
Q（0,4）= R（0,4）+ 0.8 * Max [ Q（4,3），Q（4,5）] = 0 + 0.8 * Max（0,100）= 80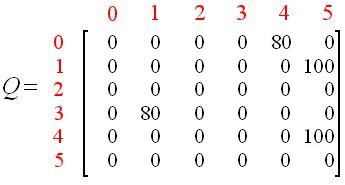

Fifth ：随机选择初始状态1

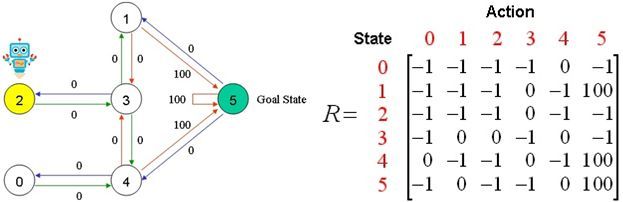
第一步：在R-table的第二列（状态1）下一跳能到达状态3、5；

第二步：随机选择下一跳，假设为状态3；

第三步：在R-table的第四列（状态3）下一跳能到达状态1、2、4；

第四步：计算Q-table，更新，；

Q（状态，动作）= R（状态，动作）+ Gamma *max[ Q（下一个状态，所有动作）]
Q（1,3）= R（1,3）+ 0.8 * Max [Q（3，1），Q（3，2），Q（3，4）] =
         0 + 0.8 * Max（0，0，0，80）= 0 + 0.8 * 80 = 64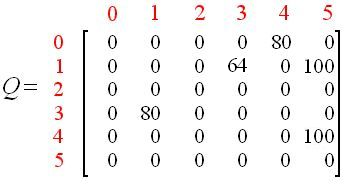

经过循环迭代，最终得到Q-table：

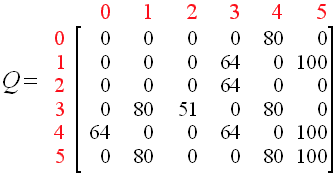
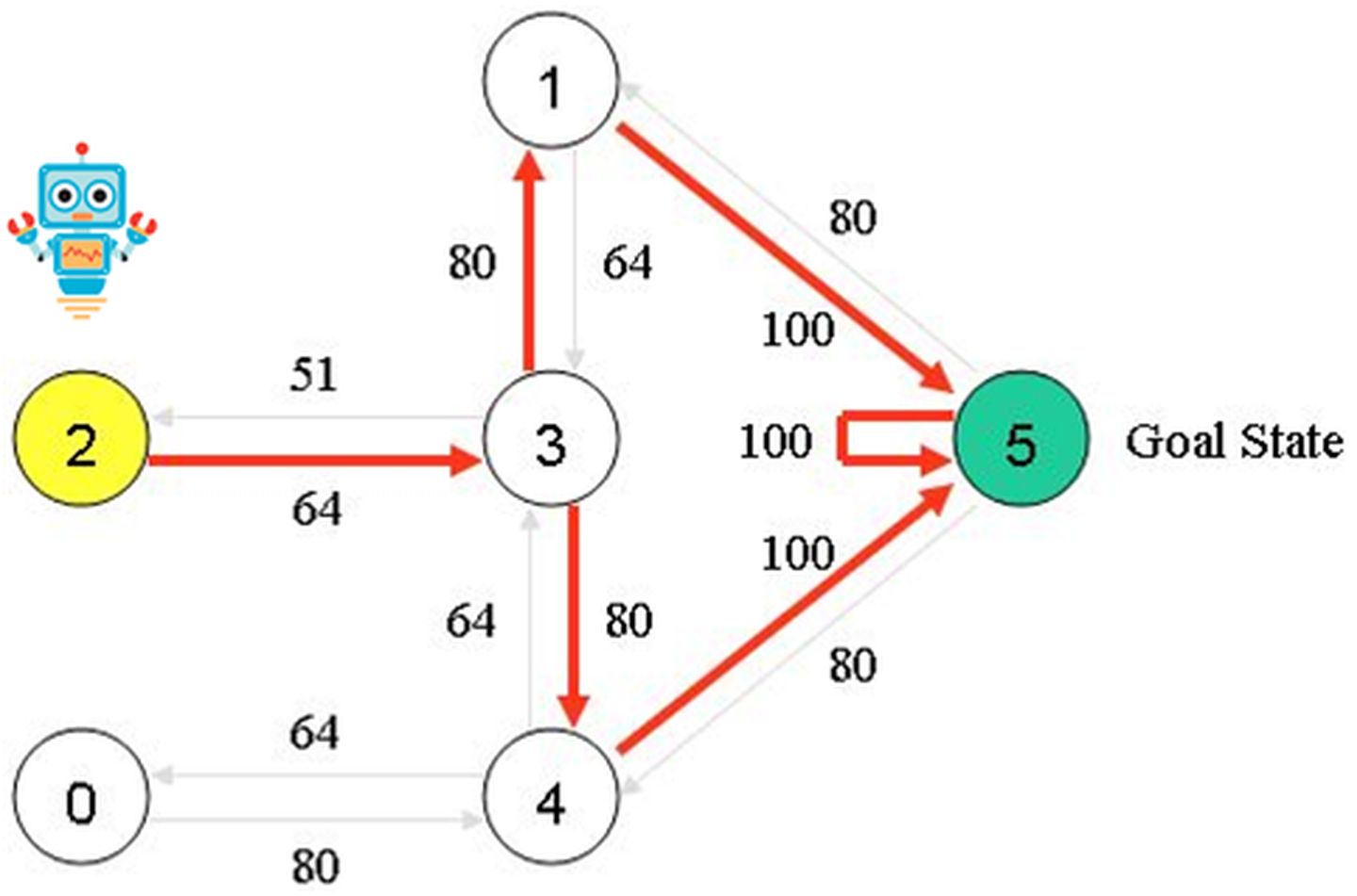
例如，从初始状态2开始，代理可以使用矩阵Q作为指导：

从状态2开始，最大Q值表明要进入状态3的动作。
从状态3开始，最大Q值表示两种选择：进入状态1或4.假设我们任意选择去1。
从状态1开始，最大Q值表明要进入状态5的动作。
因此，序列是2 - 3 - 1 - 5。

最后

以上就是懦弱板栗为你收集整理的Q学习例子的全部内容，希望文章能够帮你解决Q学习例子所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。