本期介绍????
主要介绍:计算变量在内存中存放2进制位“1”的个数的三种解法,除二取余法、 移位与1法、消1计数法,还有关于该类型题目的一些延申????。
文章目录
- 一、题目????
- 1. 除二取余法????
- 2. 移位与1法????
- 3. 消1计数法????
- 二、思路的延申????
- 1. 题目1:求两个数二进制中不同位的个数????
- 2. 题目2:打印整数二进制的奇数位和偶数位????
- 3.题目3:判断一个整数之不是2的n次方????
- 三、结论????
一、题目????
题目:输入一个整数 n ,输出该数32位二进制表示中1的个数(其中负数用补码表示)。下面我会用3种不同的方法来解决这道笔试题。
1. 除二取余法????
在数学中要将十进制数转换成二进制数老师肯定教过一种方法“ 除2取余法 ”,不知道你还记不记得。例如把89化为二进制的数:89除以2等于44余1;44除以2等于22余0;22除以2等于11余0;11除以2等于5余1;5除以2等于2余1;2除以2等于1余0;1除以2等于0余1。然后把所有余数从下往上排序后得到的结果就是89的二进制表示形式为:1011001。如下图所示:

所以这道题就可以引用此法,对于要求的数每次除2后统计余数为1的情况,这样就可以做到计算变量在内存中存放2进制位“1”的个数啦。代码如下:
#include<stdio.h>
int sta_bit_num(int n)
{
int count = 0;
while (n)
{
if (n % 2 == 1)
{
count++;
}
n /= 2;
}
return count;
}
int main()
{
int n = 0;
int count = 0;
printf("请输入要计算的数:");
scanf("%d", &n);
count = sta_bit_num(n);
printf("二进制中1的个数:%dn", count);
}

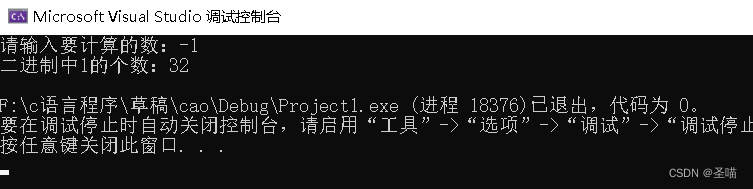
这么乍一看似乎没什么问题啊,但如果你输入负数时就会发生错误啦,就譬如输入-1。如下图所示,得出的结果为0,可我们知道-1在内存中的二进制位为32个1,所以统计的结果应该为32才对。那这是为什么呢?你看当我们输入-1时,再拿-1%2的结果必然为0,然后再除上一个2,n就变为0了然后退出循环,得到的结果必然只会是0啊兄弟们。

由于我们在编写上面这个代码的时候,压根就没有思考过负数的情况。而负数再内中存放的补码的形式与正数是不同的,所以如果还按照原先计算正数的除2取余法来计算负数必然错误。所以该如何解决这个问题呢?你想啊,这里的-1的二进制位(11111111111111111111111111111111)除了表示负数外,还可以表示一个无符号数的呀,那用除2取余法来对该无符号数进行统计是不是就间接达到效果了呀!!!所以在代码中只需要将传过去的参数n转换成无符号整数就成啦。代码如下:
#include<stdio.h>
int sta_bit_num(unsigned int n)
{
int count = 0;
while (n)
{
if (n % 2 == 1)
{
count++;
}
n /= 2;
}
return count;
}
int main()
{
int n = 0;
int count = 0;
printf("请输入要计算的数:");
scanf("%d", &n);
count = sta_bit_num(n);
printf("二进制中1的个数:%dn", count);
}

2. 移位与1法????
上面是运用数学想出来的方法,如若我在不了解除2取余法的情况下,我该如何解决这个问题呢?其实也不难,如下图所示。我们发现只要与“&”上1就可以得知被求的那个数的最低位为1还是0,然后再通过把该数右移“>>”1位,这样最后第二位就变成最后一位了,然后以此为循环,&1、>>1……最后直到被求的数为0时才停下来,这样就把每位上的1全部都统计了。
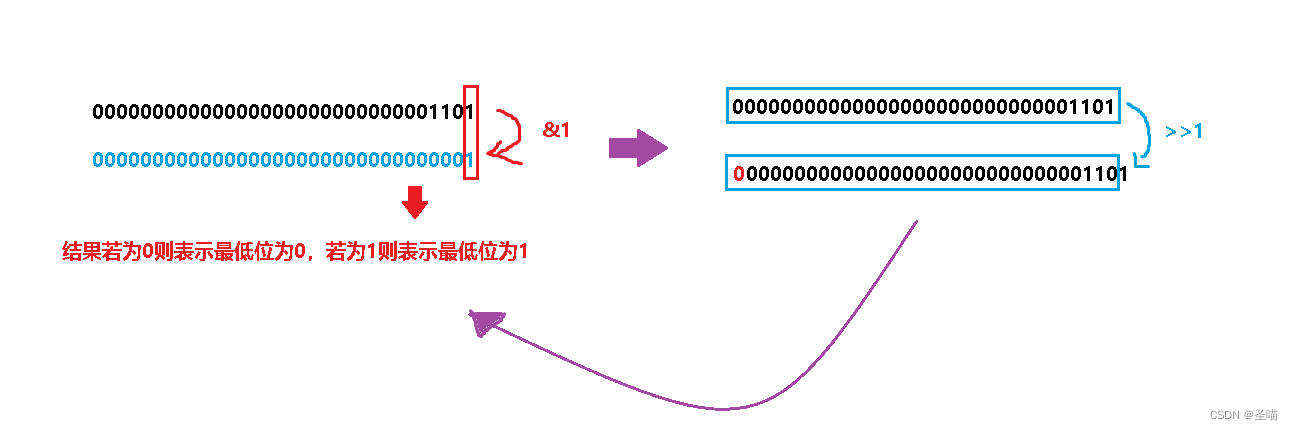
代码如下:
#include<stdio.h>
int sta_bit_num(int n)
{
int count = 0;
while (n)
{
if ((n & 1) == 1)
{
count++;
}
n >>= 1;
}
return count;
}
int main()
{
int n = 0;
int count = 0;
printf("请输入要计算的数:");
scanf("%d", &n);
count = sta_bit_num(n);
printf("二进制中1的个数:%dn", count);
}


我们调试时发现当输入为正数时结果正确,但输入为负数时程序出现新的问题,程序进入了死循环当中出不来。那这是为什么呢?因为右移操作符“>>”是分为两种的:1.算数右移,2.逻辑右移。算数右移:右边舍去,左边补充当前符号位。逻辑右移:右边舍去,左边补0。对于VS编译器的有符号整数来说“>>”其实是算数右移,而对于无符号整数来说“>>”其实是逻辑右移。所以这里当我传递接收的是int型n时,右移操作为算数右移,不管我右移多少次做左边补的都是1,而我的循环判断条件是n=0时才退出循环,这样程序当然就陷入了死循环了呀!!!
那该如何解决呢?我提供两种方法:
1. 与除2取余法的解决方案一样,把函数形参类型改为无符号型,这样再对n进行“>>”操作时就是逻辑右移了。
#include<stdio.h>
int sta_bit_num(unsigned int n)
{
int count = 0;
while (n)
{
if ((n & 1) == 1)
{
count++;
}
n >>= 1;
}
return count;
}
int main()
{
int n = 0;
int count = 0;
printf("请输入要计算的数:");
scanf("%d", &n);
count = sta_bit_num(n);
printf("二进制中1的个数:%dn", count);
}
2. 反正这里最坏的结果就是判断32个二进制位,既然怕死循环,那何不就设置一个最多循环次数为32次的循环呀?
#include<stdio.h>
int sta_bit_num(int n)
{
int count = 0;
int i = 0;
for(i=0;i<32;i++)
{
if (((n >> i) & 1) == 1)
{
count++;
}
}
return count;
}
int main()
{
int n = 0;
int count = 0;
printf("请输入要计算的数:");
scanf("%d", &n);
count = sta_bit_num(n);
printf("二进制中1的个数:%dn", count);
}
3. 消1计数法????
根据题意我们知道所需要统计的仅仅只是二进制位中1的个数,但上面两种方法在判断统计二进制位1的同时还会多余的判断二进制位0。举个例子如果我要求1,073,741,824(2 ^ 30)中二进制位1的个数,该数的二进制序列为:01000000000000000000000000000000,如果用之前的两种方法来求解该数将会判断二进制位0将近30次,而这30次是多余的动作,可见这两种方法的解题的效率其实并不太高。
而现在我将讲解一种非常牛逼的算法“ 消1计数法 ”,这个算法可并不是一般人可以想出来的。该方法是将被求的数与上一个比被求数小1的一个数,即:n & (n-1) ,你会惊讶的发现,得出的结果会让二进制序列中最低位的那个二进制位1制0。那么你想啊,如果我在多来这么几次这样的操作,是不是被求的那个数最终会变成0。以此为循环的判断条件,只要可以这样操作一次是不是就代表着二进制序列中存在着一个1呀,这样做就可以在不判断二进制位0,只判断二进制位1啦,效率不就上来了嘛。如下图所示:
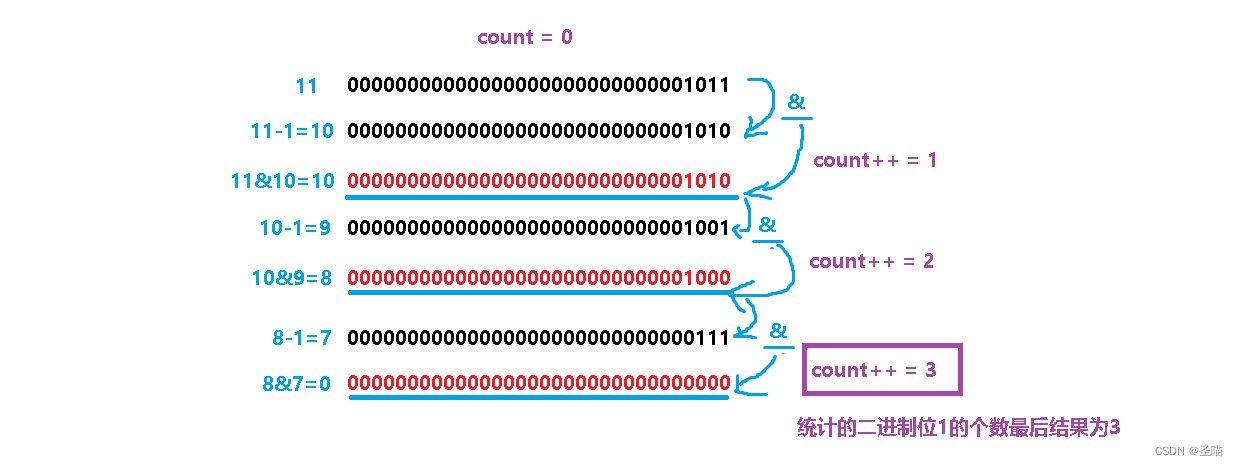
代码为:
#include<stdio.h>
int sta_bit_num(int n)
{
int count = 0;
while (n)
{
n = n & (n - 1);
count++;
}
return count;
}
int main()
{
int n = 0;
int count = 0;
printf("请输入要计算的数:");
scanf("%d", &n);
count = sta_bit_num(n);
printf("二进制中1的个数:%dn", count);
}


二、思路的延申????
在以后的学习中我们还是经常会用到上面的这种解题思路来快速的求解难题,下面我就举两个例题来说明一下:
1. 题目1:求两个数二进制中不同位的个数????
讲解编程实现:两个int(32位)整数m和n的二进制表达中,有多少个位(bit)不同?输入例子:1999 , 2299;输出例子:7。
我想大家在没看过上面的算法思路时,来求解这道题目的思路一定是逐位进行比较的是否相等,暴力求解法就是死算呀,效率太低啦。若你看过上面的解题思路,你就会豁然开朗思路一下子就延申出去了。你会发现求解这道题非常非常的简单,是需要两部就可以完成了:
第一步是用按位异或符“ ^ ”查出两个数的相异处,也就是1。
第二部就是用上面的算法来统计二进制位1的个数,相当于就是统计二进制位相异处的个数。
代码如下:
#include<stdio.h>
int sta_bit_num(int x, int y)
{
int count = 0;
int n = x ^ y;
while (n)
{
n = n & (n - 1);
count++;
}
return count;
}
int main()
{
int a = 0;
int b = 0;
int count = 0;
printf("请输入要计算的两个数:");
scanf("%d%d", &a, &b);
count = sta_bit_num(a, b);
printf("两个数二进制数中不同位的个数:%dn", count);
}
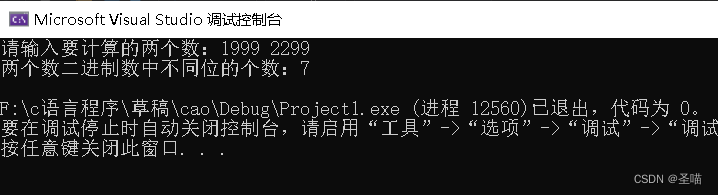
2. 题目2:打印整数二进制的奇数位和偶数位????
作业内容:获取一个整数二进制序列中所有的偶数位和奇数位,分别打印出二进制序列。
该题我们先假设二进制序列中最低位为奇数位1,然后我们想办法从高位向低位打印奇数位、偶数位。这样我们就需要两个循环分别打印奇数位和偶数位了。那该怎么获取最高位的二进制数呢?前面也讲过这种思路:只需先右移“ >> ”32位,然后再与“ & ”上一个1就可以做到了。代码如下:
#include<stdio.h>
void print_odd(unsigned int n)
{
int i = 0;
printf("打印奇数位:n");
for (i = 30; i >= 0; i -= 2)
{
printf("%d ", (n >> i) & 1);
}
printf("n");
}
void print_even(int n)
{
int i = 0;
printf("打印偶数位:n");
for (i = 31; i >= 1; i -= 2)
{
printf("%d ", (n >> i) & 1);
}
printf("n");
}
int main()
{
int n = 0;
printf("请输入一个数:");
scanf("%d", &n);
print_odd(n);
print_even(n);
return 0;
}


3.题目3:判断一个整数之不是2的n次方????
同理这道题也是可以引用上面那个计算变量在内存中存放2进制位“1”的个数的思路。我们知道2 ^ n整数的二进制序列中只可能存在一个1,因为二进制的权重就是如此。就譬如:2 ^ 1的二级制序列就是00000000000000000000000000000010,2 ^ 5的二进制序列就是00000000000000000000000000100000。所以在求一个数是否为2 ^ n的整数时,只需要判断该数的二进制序列中只存在一个1就可以了。那这里不想也知道用消1计数法最为高效。代码如下:
#include<stdio.h>
int is_pow(int n)
{
int count = 0;
while (n)
{
n = n & (n - 1);
count++;
}
return count;
}
int main()
{
int n = 0;
printf("请输入一个数:");
scanf("%d", &n);
if (is_pow(n) == 1)
{
printf("整数%d是2的n次方n", n);
}
else
{
printf("整数%d不是2的n次方n", n);
}
return 0;
}


三、结论????
我其实希望大家认真且细致的看一下我所写的这些关于典型例题的博客,因为我并不是只把代码给出来就完了,我会细致的讲解同一道题不同求解的思路,甚至有些你听都没听说过的神来之笔的解法。还有一些我自己对该问题的看法,以及通过该问题求解的思路是否还可以延申出去。

这份博客????如果对你有帮助,给博主一个免费的点赞以示鼓励欢迎各位????点赞????评论收藏⭐️,谢谢!!!
如果有什么疑问或不同的见解,欢迎评论区留言欧????。
最后
以上就是想人陪薯片最近收集整理的关于计算变量在内存中存放2进制位“1”的个数【三种解法】【详解】的全部内容,更多相关计算变量在内存中存放2进制位“1”内容请搜索靠谱客的其他文章。









发表评论 取消回复