1. 首页
  2. 文章中心
  3. 算法学习

算法学习 双指针技巧总结

134 阅读 0 评论
我是靠谱客的博主 鲤鱼巨人，这篇文章主要介绍算法学习 双指针技巧总结，现在分享给大家，希望可以做个参考。

一、快慢指针常见算法

1.判断链表中是否有环

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
给定一个链表，判断链表中是否有环。
为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。
示例 1：
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：
输入：head = [1], pos = -1
输出：false
解释：链表中没有环。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
	/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head==nullptr||head->next==nullptr)
            return false;
        
        ListNode* p_fast=head;
        ListNode* p_slow=head;
        while(p_fast!=nullptr)
        {
            p_fast=p_fast->next;
            if(p_fast!=nullptr)p_fast=p_fast->next;
            p_slow=p_slow->next;
            if(p_fast==p_slow)
                return true;
        }
        return false;
    }
};
改进代码

```cpp
class Solution {
public:
bool hasCycle(ListNode* head) 
{
	//两个运动员位于同意起点head
	ListNode* faster{ head };  //快的运动员
	ListNode* slower{ head };  //慢的运动员

	if (head == NULL)  //输入链表为空，必然不是循环链表
		return false;

	while (faster != NULL && faster->next != NULL)
	{
		faster = faster->next->next;  //快的运动员每次跑两步
		slower = slower->next;  //慢的运动员每次跑一步
		if (faster == slower)  //他们在比赛中相遇了
			return true;  //可以断定是环形道，直道不可能相遇
	}
	return false;  //快的运动员到终点了，那就是直道，绕圈跑不会有终点
}
};

2.环形链表 II

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。
说明：不允许修改给定的链表。
示例 1：
输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：
输入：head = [1,2], pos = 0
输出：tail connects to node index 0
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：
输入：head = [1], pos = -1
输出：no cycle
解释：链表中没有环。
进阶：
你是否可以不用额外空间解决此题？

可以看到，当快慢指针相遇时，让其中任一个指针指向头节点，然后让它俩以相同速度前进，再次相遇时所在的节点位置就是环开始的位置。这是为什么呢？
第一次相遇时，假设慢指针 slow 走了 k 步，那么快指针 fast 一定走了 2k 步，也就是说比 slow 多走了 k 步（环长度的倍数）。
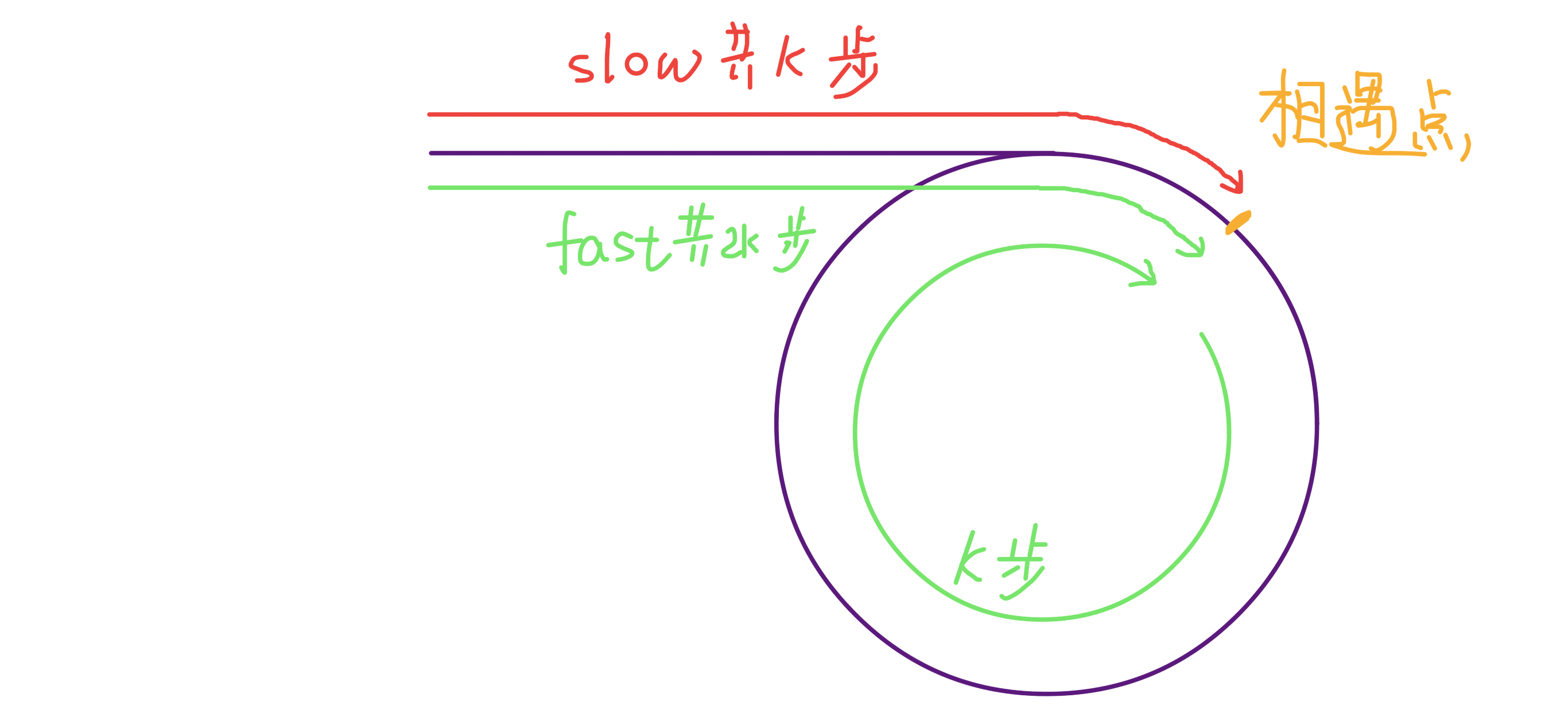
在这里插入图片描述
设相遇点距环的起点的距离为 m，那么环的起点距头结点 head 的距离为 k - m，也就是说如果从 head 前进 k - m 步就能到达环起点。
巧的是，如果从相遇点继续前进 k - m 步，也恰好到达环起点。
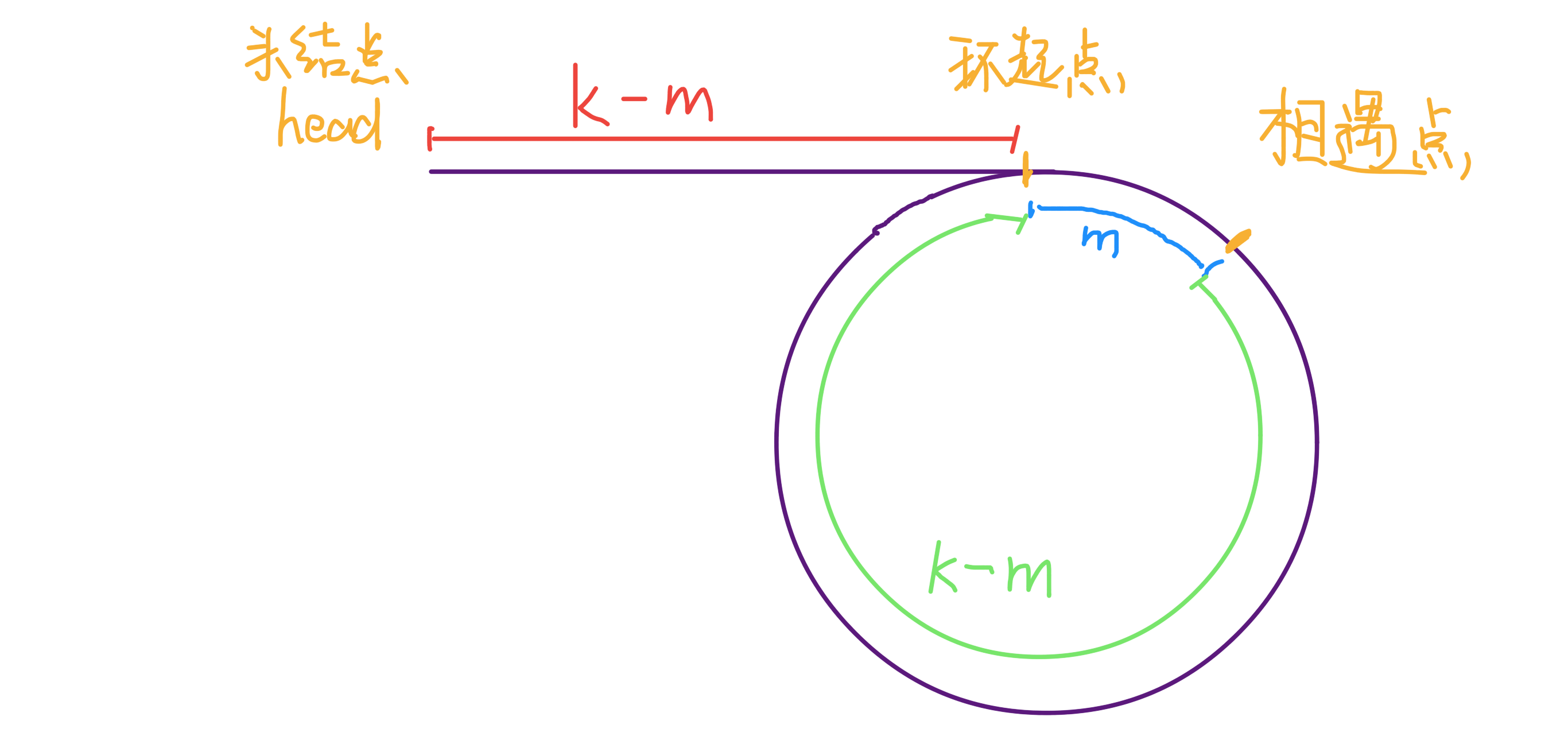
在这里插入图片描述
所以，只要我们把快慢指针中的任一个重新指向 head，然后两个指针同速前进，k - m 步后就会相遇，相遇之处就是环的起点了。

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(head==nullptr)
            return head;
        ListNode* fast=head;
        ListNode*slow=head;
        while(fast!=nullptr&&fast->next!=nullptr)
        {
            fast=fast->next->next;
            slow=slow->next;
            if(slow==fast)
            {
                slow=head;
                while(slow!=fast)
                {
                 slow=slow->next;
                 fast=fast->next;
                }
                return slow;
            }
        }
       
        return nullptr;
    }
};

3.寻找链表的中点

类似上面的思路，我们还可以让快指针一次前进两步，慢指针一次前进一步，当快指针到达链表尽头时，慢指针就处于链表的中间位置。

复制代码
1
2
3
4
5
6
7
while (fast != null && fast.next != null) {
    fast = fast.next.next;
    slow = slow.next;
}
// slow 就在中间位置
return slow;

当链表的长度是奇数时，slow 恰巧停在中点位置；如果长度是偶数，slow 最终的位置是中间偏右：
center
寻找链表中点的一个重要作用是对链表进行归并排序。
回想数组的归并排序：求中点索引递归地把数组二分，最后合并两个有序数组。对于链表，合并两个有序链表是很简单的，难点就在于二分。
但是现在你学会了找到链表的中点，就能实现链表的二分了。关于归并排序的具体内容本文就不具体展开了。

4.寻找链表的倒数第k个元素

我们的思路还是使用快慢指针，让快指针先走 k 步，然后快慢指针开始同速前进。这样当快指针走到链表末尾 null 时，慢指针所在的位置就是倒数第 k 个链表节点（为了简化，假设 k 不会超过链表长度）：

复制代码
1
2
3
4
5
6
7
8
9
10
11
ListNode slow, fast;
slow = fast = head;
while (k-- > 0) 
    fast = fast.next;

while (fast != null) {
    slow = slow.next;
    fast = fast.next;
}
return slow;

二、左右指针的常用算法

左右指针在数组中实际是指两个索引值，一般初始化为 left = 0, right = nums.length - 1 。

1.二分查找

2.两数之和

在这里插入图片描述
只要数组有序，就应该想到双指针技巧。这道题的解法有点类似二分查找，通过调节 left 和 right 可以调整 sum 的大小

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int[] twoSum(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left < right) {
        int sum = nums[left] + nums[right];
        if (sum == target) {
            // 题目要求的索引是从 1 开始的
            return new int[]{left + 1, right + 1};
        } else if (sum < target) {
            left++; // 让 sum 大一点
        } else if (sum > target) {
            right--; // 让 sum 小一点
        }
    }
    return new int[]{-1, -1};
}

3.反转数组

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
void reverse(int[] nums) {
    int left = 0;
    int right = nums.length - 1;
    while (left < right) {
        // swap(nums[left], nums[right])
        int temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp;
        left++; right--;
    }
}

4.滑动窗口

这也许是双指针技巧的最高境界了，如果掌握了此算法，可以解决一大类子字符串匹配的问题，不过「滑动窗口」稍微比上述的这些算法复杂些。

幸运的是，这类算法是有框架模板的，而且这篇文章就讲解了「滑动窗口」算法模板，帮大家秒杀几道 LeetCode 子串匹配的问题。

5.两个数组的交集 II

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
给定两个数组，编写一个函数来计算它们的交集。

示例 1:

输入: nums1 = [1,2,2,1], nums2 = [2,2]
输出: [2,2]
示例 2:

输入: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出: [4,9]
说明：

输出结果中每个元素出现的次数，应与元素在两个数组中出现的次数一致。
我们可以不考虑输出结果的顺序。
进阶:

如果给定的数组已经排好序呢？你将如何优化你的算法？
如果 nums1 的大小比 nums2 小很多，哪种方法更优？
如果 nums2 的元素存储在磁盘上，磁盘内存是有限的，并且你不能一次加载所有的元素到内存中，你该怎么办？
  1. 排序+双指针
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        if(nums1.size()==0||nums2.size()==0)
            return vector<int>{};
        sort(nums1.begin(),nums1.end());
        sort(nums2.begin(),nums2.end());
        int nums1_left=0;
        int nums2_left=0;
        vector<int>ret;
        while(nums1_left<nums1.size()&&nums2_left<nums2.size())
        {
            if(nums1[nums1_left]==nums2[nums2_left])
            {
                 ret.push_back(nums1[nums1_left]);
                nums1_left++;
                nums2_left++;
            }else if(nums1[nums1_left]>nums2[nums2_left])
                nums2_left++;
            else
                nums1_left++;
        }
     return ret;
    }
};
  1. 哈希表
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        if(nums1.size()==0||nums2.size()==0)
            return vector<int>{};
            vector<int>ret;
        unordered_map<int,int>hash;
        for(int i=0;i<nums1.size();i++)
        {
            auto ptr=hash.find(nums1[i]);
            if(ptr==hash.end())
            {
                hash.insert(make_pair(nums1[i],1));
            }else
                ptr->second++;
        }
        for(int i=0;i<nums2.size();i++)
        {
            auto ptr=hash.find(nums2[i]);
            if(ptr==hash.end())
                continue;
            else if(ptr->second==0)
                continue;
            else{
                ret.push_back(ptr->first);
                ptr->second--;
            }
        }

        return ret;
    }
};

最后

以上就是鲤鱼巨人最近收集整理的关于算法学习 双指针技巧总结的全部内容，更多相关算法学习内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(89)

相关文章

双指针应用之旋转链表
双指针应用之旋转链表
LeetCode 92. 反转链表 II（双指针）
LeetCode 92. 反转链表 II（双指针）
C实现 LeetCode->Reverse Linked List II （双指针大法）(单链表反转)
C实现 LeetCode->Reverse Linked List II （双指针大法）(单链表反转)
LeetCode 61. 旋转链表（Java）
LeetCode 61. 旋转链表（Java）
算法学习 双指针技巧总结
算法学习 双指针技巧总结
leetcode算法总结 —— 双指针
leetcode算法总结 —— 双指针
LeetCode双指针算法总结1一、盛水最多的容器二、三数之和三、最接近的三数之和四、四数之和
LeetCode双指针算法总结1一、盛水最多的容器二、三数之和三、最接近的三数之和四、四数之和
LeetCode-双指针总结
LeetCode-双指针总结

评论列表共有 0 条评论

立即
投稿
返回
顶部