序言

本文是对2021年秋季CS224W课程slides的速记，没有作业的解答。

CS224W其实看下来更偏向于是理论计算机方向的研究（比如图论），而非重点在图神经网络，因此很多内容理论性很强，本文是笔者花两天时间速过了一遍记录的一些对自己有用的要点，更偏向于图神经网络应用方面的摘要，一些没看懂的部分暂时没有深入研讨，仅先留个印象。

课程链接：http://web.stanford.edu/class/cs224w/

---

---

节点中心度

给定无向图$G=(V,E)$，节点$v$的中心度（centrality）$c_v$用于衡量节点$v$的重要性，具体有如下几种计算方式：

1. 特征向量中心度（eigenvector centrality）：节点重要性由与它相邻节点的重要性决定
   $$c_v=\frac{1}{\lambda }\sum _{u\in N(v)}{c}_u\in \mathbb{R}$$
   其中$N(v)$表示节点$v$的邻接点，$\lambda >0$为标准化系数。

   求解上式等价于求解$\lambda \mathbf{c}=A\mathbf{c}$，其中$A$为无向图$G$的邻接矩阵，因此等价于求解$A$的特征值与特征向量，根据Perron-Fronbenius定理可知，${\lambda }_{\max }$必然为正，则通常使用最大特征值${\lambda }_{\max }$对应的特征向量${\mathbf{c}}_{\max }$作为式$(1)$的解。

2. 中介中心度（betweenness centrality）：节点重要性由它中转多少对节点之间的最短路径决定
   $$c_v=\sum _{s\ne v\ne t}\frac{\text{count(shortest paths between }s\text{ and }t\text{ that contain }v)}{\text{count(shortest paths between }s\text{ and }t)}\text{\hspace{1em}(2)}$$
   如在无向图$(A,C),(B,C),(C,D),(B,D),(D,E)$中，$c_A=c_B=c_E=0,c_C=c_D=3$

3. 紧密中心度（closeness centrality）：节点重要性由它与所有其他节点的距离之和决定
   $$c_v=\frac{1}{{\sum }_{u\ne v}\text{shortest path length between }u\text{ and }v}$$
   如在无向图$(A,C),(B,C),(C,D),(B,D),(D,E)$中，$c_A=1/8,c_D=1/5$

---

图基元

1. 首先定义图的同形（isomorphism）：称两个节点数相等的图$G_1=(V_1,E_1)$与$G_2=(V_2,E_2)$是同形的，若存在一一映射$f:V_1\to V_2$，使得$E_1=E_2$（比如五角星和五边形就是同形图）。

   判断两个图是否同形是NP-hard

2. 图基元（graphlets）：非同形的图构成的集合。

   

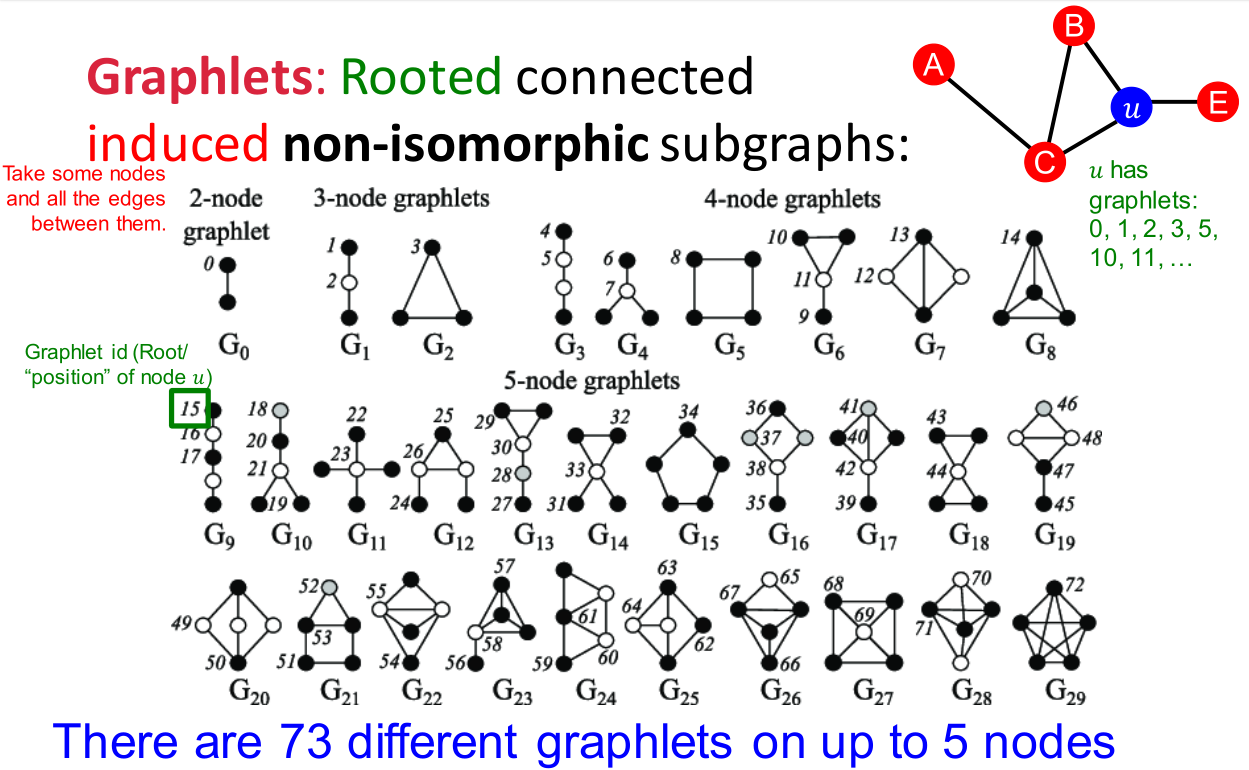
   比如上图中陈列节点数不超过$5$的所有图基元，节点上标号记录不同类型的图基元节点（如$G_8$中的$4$个节点本质上是同类）。

   节点数	图基元数量	累积不同图基元节点数量
   $2$	$1$	$1$
   $3$	$2$	$4$
   $4$	$6$	$15$
   $5$	$21$	$73$

   事实上图基元未必一定是连通图，但是上图和上表中统计的都是连通情况下的计数。

3. 图基元度向量（graphlet degree vectors，GDV）：

   节点$u$的GDV由它所在的子图中不同图基元节点出现频率构成。

   

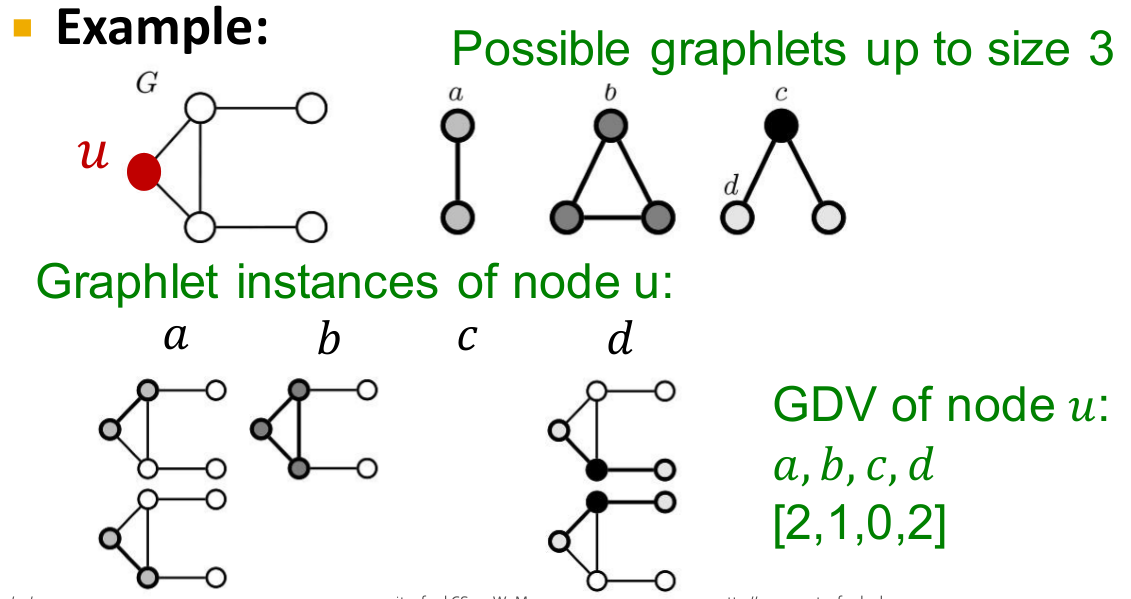
   如上图所示，只考察节点数不超过$3$的图基元，共计$4$种不同的图基元节点$a,b,c,d$，考察节点$u$分别作为这四类节点出现的次数，得到的GDV为$[2,1,0,2]$

---

计算两个节点之间路径总数的巧解

定义无向图$G=(U,V)$邻接矩阵$A$：
$$A_{uv}=\{\begin{array}{rlrl}& 1& & \text{if }u\in N(v)\\ & 0& & \text{if }u\notin N(v)\end{array}$$
定义路径计数矩阵$P^{(n)}$：
$$P_{uv}^{(n)}=\text{count(paths of length }n\text{ between}u\text{ and }v)$$
则可以证明$P^{(n)}=A^n$，这里的路径可以不是简单路径（即路径重可以存在环或重复边）。

可以通过数学归纳法证明：
$$P_{uv}^{(n+1)}=\sum _{w\in V}{A}_{uw}{P}_{wv}^{(n)}=\sum _{w\in V}{A}_{uw}(A^n{)}_{wv}=A^{n+1}$$
结论在有向图上同样适用，得到的$P^{(1)},P^{(2)},...$称为Katz索引。

---

图核

图核（graph kernels）用于衡量图的相似性。

举个最简单的例子，对于两个图$G_1=(V_1,E_1)$与$G_2=(V_2,E_2)$，执行某种图分解算法$\mathcal{F}$：
F ( G 1 ) = { S 11 , S 12 , . . . , S 1 n 1 } F ( G 2 ) = { S 21 , S 22 , . . . , S 1 n 2 } mathcal{F}(G_1)={S_{11},S_{12},...,S_{1n_1}}\ mathcal{F}(G_2)={S_{21},S_{22},...,S_{1n_2}}\ F(G1​)={S11​,S12​,...,S1n1​​}F(G2​)={S21​,S22​,...,S1n2​​}
基于分解得到的子图，定义核值（kernel value）：
$$k_R(G_1,G_2)=\sum _{i=1}^{n_1}\sum _{j=1}^{n_2}\delta (S_{1i},S_{2j})$$
其中$\delta$函数在两子图同构时取$1$，否则取$0$，这样就将大的图同构问题转化为小的图同构问题，不同的分解算法$\mathcal{F}$和不同的同构定义$\delta$可以得到不同的图核计算方式。

此外还可以使用一些其他的图特征向量表示手段：

1. 统计图中不同度数的节点数量，构成一个特征向量；

2. 统计图中不同图基元的数量，构成一个特征向量；

   笔者注：图基元的统计是非常复杂的，若图节点度数不超过$d$，则统计节点数不超过$k$的图基元的时间复杂度为$O(|V|d^{k-1})$；

然后计算特征向量之间的相似度。

最后一种经典的算法是重染色（color refinement）：

1. 首先给全图每一个节点都染上初始颜色$c^{(0)}(v)$

2. 然后进行$n$轮迭代染色（$n$为超参数）：
   c ( k + 1 ) ( v ) = Hash ( { c ( k ) ( v ) , { c ( k ) ( u ) } u ∈ N ( v ) } ) c^{(k+1)}(v)=text{Hash}({c^{(k)}(v),{c^{(k)}(u)}_{uin N(v)}}) c(k+1)(v)=Hash({c(k)(v),{c(k)(u)}u∈N(v)​})
   其中$\mathrm{H}\mathrm{a}\mathrm{s}\mathrm{h}$函数将不同的输入映射成不同的数值；

3. 最后将具有同样染色序列（即 { c ( 0 ) ( v ) , c ( 1 ) ( v ) , . . . , c ( n ) ( v ) } {c^{(0)}(v),c^{(1)}(v),...,c^{(n)}(v)} {c(0)(v),c(1)(v),...,c(n)(v)}）的节点定义为同类型的节点，统计各类型节点的数量构成特征向量；

这种算法运行速度要远远快于统计图基元的做法。

---

节点嵌入之随机游走

随机游走（random walks）的思想源于如果从$u$出发大概率能走到$v$，那么这表明两个节点是相似的。

首先定义几个标记：

1. $z_u$：表示节点$u$的嵌入；

2. $P(v|z_u)$：从节点$u$出发，随机游走到节点$v$的（预测）概率；

那么我们认为$z_u^{\top }{z}_v$近似等于$u$和$v$将会同时出现在一条随机游走路径中的概率。通常我们会固定随机游走的长度为一个固定值且不会太大，长度为$1$时退化为邻接点搜索。

具体而言，从节点$u$出发，根据某种随机游走的策略进行序列生成，然后优化各个节点的嵌入表示以拟合上述概率：
$${\text{maximize}}_{f:u\to {\mathbb{R}}^d}\sum _{u\in V}\log P(N_R(u)|z_u)$$
其中$f$是节点嵌入映射，$N_R(u)$表示从节点$u$出发，在策略$R$下随机游走能够抵达的所有近邻（neighborhood），实际仿真中$N_R(u)$就等于从节点$u$出发抵达的节点集合。

上式中的目标函数本质上就是最大似然，即给定节点$u$的情况下，预测它的近邻节点：
$$\mathcal{L}=\sum _{u\in V}\sum _{v\in N_R(u)}-\log (P(v|z_u))$$
我们可以使用softmax函数来计算上式中的概率值：
$$P(v|z_u)=\frac{\exp (z_u^{\top }{z}_v)}{{\sum }_{n\in V}\exp (z_u^{\top }{z}_n)}$$
这里又提到计算softmax函数的复杂度很高（主要是分母的计算太复杂），因此需要做负采样：
$$\log \left(\frac{\exp (z_u^{\top }{z}_v)}{{\sum }_{n\in V}\exp (z_u^{\top }{z}_n)}\right)\approx \log (\sigma (z_u^{\top }{z}_v))-\sum _{i=1}^k\log (\sigma (z_u^{\top }{z}_{n_i}))$$
其中$\sigma (\cdot )$是sigmoid激活函数，$n_i\sim P_V$是随机采样得到的节点，此时无需计算softmax分母上所有节点的点积，只需要对采样得到的$k$个随机负样本$n_i$进行计算即可。负样本量$k$的取值通常在$5$到$20$，采样概率分布与节点的度数成正比。

最后说明随机游走策略$R$的选取，这里只介绍一种偏差随机游走（biased random walks）方法：

• 每次定义往回走（即回到前一个节点）的概率$1/p$和不往回走的概率$1/q$

• 对于偏向于广度优先搜索的随机游走，赋予$p$以较低的值（即大概率往回走）；

• 对于偏向于深度优先搜索的随机游走，赋予$q$以较低的值（即大概率往下走）；

这里的概率都是未经标准化过的概率，一般来说会在往下走的节点里面找到一个节点编号最小的（即深度优先搜索默认的下一个节点）来赋予它的概率权重为$1$（同样是未经标准化的），然后将一大堆$1/q$和$1,1/p$进行标准化后得到最终的概率值。

一些其他随机游走方法的相关研究：

1. 不同种类的偏差随机游走：

   基于节点属性：参考文献

   基于学习到的权重：参考文献

2. 其他优化方法：

   直接基于一级（one-hop）和二级（two-hop）的随机游走概率：参考文献

3. 网络处理技术：

   在各种原始网络变体上运行随机游走：参考文献，参考文献

---

整图嵌入

1. 方法一：计算每个节点的嵌入并累和。
   $$z_G=\sum _{v\in V}{z}_v$$
   这个方法在参考文献中有使用。

2. 方法二：引入一个虚拟节点来表示整图（或子图），然后计算虚拟节点的嵌入。

   这个方法似乎只能用于子图嵌入的学习，整图就只有一个虚拟节点无法学习。在参考文献首次提出。

3. 方法三：匿名游走嵌入（anonymous walk embeddings）。

   参考文献首次提出，具体操作如下所示：

   • 首先还是若干次随机游走采样，只不过这次记录随机游走的节点序列的方式稍有变化，一般情况下我们记录的是ABCBC，这里因为是匿名，所以记录为$12312$，注意到在匿名的情况下ABCBC与DEFEF是完全没有区别的。

   • 在匿名的条件下，不同长度的随机游走序列的数量如下图所示：

     随机游走序列长度	不同随机游走序列数量
     $2$	$2$
     $3$	$5$
     $4$	$15$
     $5$	$52$
     $6$	$203$
     $7$	$877$
     $8$	$3\times 10^3$
     $9$	$2.1\times 10^4$
     $10$	$1.16\times 10^5$
     $11$	$6.79\times 10^5$
     $12$	$4\times 10^6$

     以长度为$3$为例，不同的序列有$111,112,121,122,123$

   • 然后以匿名的方式，采样$m$条随机游走路径（用于刻画图的一个概率分布）：
     $$m=\lceil \frac{2}{{ϵ}^2}(\log (2^{\eta }-2)-\log (\delta ))\rceil$$
     其中$\eta$是上表中给定长度的匿名随机游走序列的种类数（如采样长度为$7$时$\eta =877$），并期望有不超过$\delta$的概率得到的分布误差超过$ϵ$

   • 接着直接学习每一条匿名随机游走序列的嵌入表示$z_i,i=1,...,\eta$

   • 最后将学习得到的所有$z_i$通过某种运算得到整图嵌入$z_G$：
     $${\text{maximize}}_{z_G}\sum _{t=\Delta +1}^T\log P(w_t|w_{t-\Delta },...,w_{t-1},z_G)$$
     上式中目标函数的含义是来预测在一个大小为$\Delta$的窗口内，同一个匿名随机游走序列同时出现的概率，$T$表示采样得到的随机游走序列的数量。

     举个例子，采样得到$w_1=1232,w_2=1234,w_3=1232,w_4=1212$，固定$\Delta =2$，则预测$w_3$在给定$w_1,w_2$下出现的概率。

   • 但是提出文里的操作稍有区别，这里的采样通常是从一个固定节点$u$出发，采样$T$条长度为$l$的随机游走序列：
     N R ( u ) = { w 1 u , w 2 u . . . , w T u } N_R(u)={w_1^u,w_2^u...,w_T^u} NR​(u)={w1u​,w2u​...,wTu​}
     然后预测随机游走序列同时出现在大小为$\Delta$的窗口内的概率，$w_i$的嵌入为$z_i$：
     $${\text{maximize}}_{z_i,z_G}\frac{1}{T}\sum _{t=\Delta }^T\log P(w_t|w_{t-\Delta },...,w_{t-1},z_G)$$
     其中：
     $$\begin{gathered} P(w_t|w_{t-\Delta },...,w_{t-1},z_G)=\frac{\exp (y(w_t))}{{\sum }_{i=1}^{\eta }\exp (y(w_i))} \\ y(w_t)=b+U\cdot \left(\text{concat}\left(\frac{1}{\Delta }\sum _{i=1}^{\Delta }{z}_i,z_G\right)\right) \end{gathered}$$
     同理上式softmax概率的计算依然需要使用负采样来简化，$\text{concat}$部分的意思是先将各个随机游走序列的嵌入取均值，再和整图嵌入$z_G$拼接起来，$b\in \mathbb{R},U\in {\mathbb{R}}^D$是需要学习的参数，其实就是一个全连接层。

   • 最终我们得到了整图嵌入$z_G$，有人可能以为$z_G$就是各个$z_i$加权求和或者拼接得到的，提出文里说得很明确，$z_G$和$z_i$一样，都是独立的决策变量。

---

PageRank算法

计算PageRank的方法有点类似计算马尔可夫链中的稳态概率，原始的PageRank做了一个很强的假定，即一个页面指出去的所有链接都是等权重的，这构成了一个特殊的马尔克夫矩阵$M$。然后计算$r=Mr$即可得到所有页面的权重构成的权重向量$r$

求解$r=Mr$有很多近似迭代算法，最简单的方法就是初始化$r$是等权重的，然后每次迭代$r\leftarrow Mr$即可收敛。

但是PageRank算法存在两个问题：

1. 页面是死胡同（没有指出链接），就会造成页面重要性泄漏；

   解决方案：让死胡同节点以等概率指向所有其他页面。

2. 页面所有的指出链接都属于同一个group，即存在一大堆页面构成的孤岛区域，此时页面重要性就会被这个孤岛吸收掉，这称为蛛网陷阱（spider traps）。

   解决方案：每次随机游走以小概率跳到随机页面中。
   $$\begin{gathered} r_j=\sum _{i\to j}\frac{r_i^{(t)}}{d_i}⟶r_j=\sum _{i\to j}\beta \cdot \frac{r_i^{(t)}}{d_i}+(1-\beta )\cdot \frac{1}{N} \\ r=Mr⟶\beta M+(1-\beta ){\left[\frac{1}{N}\right]}_{N\times N} \end{gathered}$$
   一般$\beta =0.8,0.9$

非常简单的例子，两个页面，$a\to b$，此时就会发生死胡同问题；如果是$a\to b,b\to b$，则会发生蛛网陷阱问题。

---

二分图推荐

常见的商品和用户（购买与评分）会构成二分图的关系，根据这样的关系可以对用户进行商品推荐，如查询与某个商品关联度最高的另一个商品。

从路径的角度来看，可以计算两个商品之间的距离，但是只看距离肯定是不够的，比如两个商品被同一个人购买，与两个商品被同一群人购买，这两个商品的相似度肯定是不一样的。

因此类似PageRank，我们认为每个商品都有一个重要性，可以通过随机游走来衡量这种重要性，算法代码如下：

item = QUERY_NODES.sample_by_weight()
for i in range(N_STEPS):
    user = item.get_random_neighbor()
    item = user.get_random_neighbor()
    item.visit_count += 1
    if random() < ALPHA:	# 跳转
        item = QUERY_NODES.sample_by_weight()

比如上面代码从 QUEY_NODES = { Q } text{QUEY_NODES}={Q} QUEY_NODES={Q}出发，设定$\text{ALPHA}=0.5$，我们可以统计每个商品被访问的次数，然后即可得到与$Q$相似度最高的商品集合。

这种算法考虑到了商品和用户之间的多重联系、多重路径，直接与间接联系，因此是具有很高可信度的。

---

节点分类之消息传递

1. 场景：图中一些节点已有标签，如何给其他节点赋上标签？

2. 算法：
   $$P(Y_v=c)=\frac{1}{{\sum }_{(v,u)\in E}{A}_{v,u}}\sum _{(v,u)\in E}{A}_{v,u}P(Y_u=c)$$
   其中$Y_v$表示节点$v$的标签，$A$是邻接矩阵（值可以是边的权重）。

   这样就将每个节点的标签信息进行了传播。

   注意上式的收敛性不能得到保证。

3. 具体而言，首先将每个节点的标签概率赋好，有标签的直接给对应标签赋确定概率，没有标签的给每个标签赋等概率值。然后通过上面的消息传递算法进行迭代。

当然节点分类也可以直接用节点的特征向量来表示（用$z_v$来预测$Y_c$），有一个经典算法是迭代分类器（iterative classifier），在迭代过程中不断修正$z_v$和$Y_c$，不过个人觉得直接用机器学习来得容易些。

后面还有一个Correct & Smooth的分类器，重点是预测分类完之后做的后处理算法，看起来很高端，但是我觉得好像没有什么用，感觉很像是对训练残差做二次训练。找到一篇论文精读和实现的博客，可以参考，不一定有用。

---

置换等变异性

置换等变异性（permutation equivariance）是说图节点本身没有次序可言，定义一个图$G=(A,X)$，其中$A$是邻接矩阵，$X$是所有节点特征向量拼成的特征矩阵，对于不同次序的节点编号，$A,X$的行列可能是需要置换的，那么如果存在一个函数$f$，使得对于任意两个不同次序的节点编号得到的$A_i,X_i$和$A_j,X_j$，都有$f(A_i,X_i)=f(A_j,X_j)$成立，则称$f$是置换等变异性函数。

---

GCN（mean-pool）

[Kipf & Welling, ICLR 2017]

• 思想：节点的近邻定义了一个计算图（computational graph），即每个节点可以根据近邻的边来聚合近邻的信息。

• 基本方法：对近邻节点的信息取平均实现消息传递。
  $$h_v^{(k+1)}=\sigma \left(W_k\sum _{u\in N(v)}\frac{h_u^{(k)}}{|N(v)|}+B_k{h}_v^{(k)}\right)k=0,1,...,K-1$$
  其中$h_v^{(n)}$是节点$v$在网络第$n$层的信息，$K$是总网络层数，$W_k$和$B_k$是可学习的参数。

  通过某种方法初始化$h_v^{(0)}$，最后一层的输出作为节点嵌入$z_v=h_v^{(K)}$

  可以改写为矩阵形式：
  $$H^{(k+1)}=\sigma (\tilde{A}{H}^{(k)}{W}_k^{\top }+H^{(k)}{B}_k^{\top })$$
  其中$H^{(k)}=[h_1^{(k)},...,h_{|V|}^{(k)}{]}^{\top },\tilde{A}=D^{-1}A$，$D$是节点度数对角矩阵。

• 图卷积层是置换等变异性函数

• 一般损失函数可以定义为：
  $$\mathcal{L}=\sum _{z_u,z_v}\text{CE}(y_{u,v},\text{DEC}(z_u,z_v))$$
  其中$y_{u,v}$是标签值，在$u,v$相似时标注为$1$，否则为$0$（其实一般只有$u=v$才标注为$1$），$\text{DEC}$可以理解为向量内积，外面套着的是交叉熵。

• 与CNN的对比：显然CNN就是一种特殊的GNN。

• 与Transformer的对比：事实上Transformer也可以看作是一种特殊的GNN，它的计算图就是一个完全图（所有输入分词看作节点，节点之间相互有边相连）。

---

消息计算与消息聚合

广义上的GNN网络层的逻辑由消息计算和消息聚合两步组成，合在一起就是消息传递。

1. 消息计算：
   m u ( l ) = MSG ( l ) ( h u ( l − 1 ) ) u ∈ { N ( v ) ∪ v } m_u^{(l)}=text{MSG}^{(l)}(h_u^{(l-1)})quad uin{N(v)cup v} mu(l)​=MSG(l)(hu(l−1)​)u∈{N(v)∪v}
   每个节点生成信息，用于传递给其他节点，最简单的形式如$m_u^{(l)}=W^{(l)}{h}_u^{(l-1)}$

2. 消息聚合：
   h v ( l ) = AGG ( { m u ( l ) , u ∈ N ( v ) } ) h_v^{(l)}=text{AGG}({m_u^{(l)},uin N(v)}) hv(l)​=AGG({mu(l)​,u∈N(v)})
   简单的聚合函数$\text{AGG}$可以是求和、取平均、取最大值等。

   这里有一个问题就是我们可能担心节点$v$自己的信息发生丢失，因此常见的改进可以是：
   h v ( l ) = CONCAT ( AGG ( { m u ( l ) , u ∈ N ( v ) } ) , m v ( l ) ) h_v^{(l)}=text{CONCAT}(text{AGG}({m_u^{(l)},uin N(v)}),m_v^{(l)}) hv(l)​=CONCAT(AGG({mu(l)​,u∈N(v)}),mv(l)​)
   即直接把上一层节点$v$产生的消息拼接进来。

通常来说GNN中进行BatchNorm和Dropout（随机丢弃图中节点，剩下节点构成子图）也是很必要的。

---

GraphSage（max-pool）

[NeurIPS 2017]

GCN显然可以套用上面的形式，记录一个常用的GraphSAGE层：
h v ( l ) = σ ( W ( l ) ⋅ CONCAT ( h v ( l − 1 ) , AGG ( { h u ( l − 1 ) , ∀ u ∈ N ( v ) } ) ) ) h_v^{(l)}=sigma(W^{(l)}cdottext{CONCAT}(h_v^{(l-1)},text{AGG}({h_u^{(l-1)},forall uin N(v)}))) hv(l)​=σ(W(l)⋅CONCAT(hv(l−1)​,AGG({hu(l−1)​,∀u∈N(v)})))
常用的聚合方法有：

1. 平均：
   $$\text{AGG}=\sum _{u\in N(v)}\frac{h_u^{(l-1)}}{|N(v)|}$$

2. 池化：
   AGG = MEAN ( { MLP ( h u ( l − 1 ) , ∀ u ∈ N ( v ) ) } ) text{AGG}=text{MEAN}({text{MLP}(h_u^{(l-1)},forall uin N(v))}) AGG=MEAN({MLP(hu(l−1)​,∀u∈N(v))})

3. LSTM：
   $$\text{AGG}=\text{LSTM}([h_u^{(l-1)},\forall u\in \pi (N(v))])$$
   $\pi$表示对近邻进行打乱顺序。

此外GraphSage中对隐层状态进行正则化：
$$h_v^{(l)}\leftarrow \frac{h_v^{(l)}}{\Vert h_v^{(l)}{\Vert }_2}$$
否则生成的节点嵌入的尺度会不一样。

---

GAT

图注意力网络（Graph Attention Networks，GAT）：
$$h_v^{(l)}=\sigma \left(\sum _{u\in N(v)}{\alpha }_{vu}{W}^{(l)}{h}_u^{(l-1)}\right)$$
在GCN或GraphSage中，${\alpha }_{vu}=1/|N(v)|$是等权重的，这里会类似注意力机制，根据节点相似性一个注意力权重。

一些常见的做法：

1. 定义注意力函数$a$，得到一个得分值：
   $$e_{vu}=a(W^{(l)}{h}_u^{(l-1)},W^{(l)}{h}_v^{(l-1)})$$
   比如可以是：
   $$e_{vu}=\text{Linear}(\text{Concat}(W^{(l)}{h}_u^{(l-1)},W^{(l)}{h}_v^{(l-1)}))$$

2. 使用softmax函数计算得分值的权重分布：
   $${\alpha }_{vu}=\frac{\exp (e_{vu})}{{\sum }_{w\in N(v)}\exp (e_{vw})}$$

此外还可以是多头注意力，即多用几个不同的注意力函数$a$，生成不同的权重${\alpha }_{vu}$，然后对结果取聚合：
$$\begin{array}{r}{h}_{v1}^{(l)}=\sigma \left(\sum _{u\in N(v)}{\alpha }_{vu}^1{W}^{(l)}{h}_u^{(l-1)}\right)\\ h_{v2}^{(l)}=\sigma \left(\sum _{u\in N(v)}{\alpha }_{vu}^2{W}^{(l)}{h}_u^{(l-1)}\right)\\ h_{v3}^{(l)}=\sigma \left(\sum _{u\in N(v)}{\alpha }_{vu}^3{W}^{(l)}{h}_u^{(l-1)}\right)\end{array}\}\Rightarrow h_v^{(l)}=\text{AGG}(h_{v1}^{(l)},h_{v2}^{(l)},h_{v3}^{(l)})$$
比如$\text{AGG}$函数可以直接就是拼接，这样信息损失得最少。

---

GNN使用技巧

1. 图结构增强：

   ① 图太稀疏，则添加虚拟节点或虚拟边（比如将二级近邻之间也连上边，或者直接$A+A^2$）。

   ② 图太稠密，则消息传递时选择对近邻进行采样。

   ③ 图太庞大，则采样子图计算子图的嵌入，如可以通过重复的随机游走来采样，但要尽可能保持原始图的连通性（从消息传递的角度来说是这样的）。

2. 图特征增强：比如使用节点的度数、聚类稀疏、PageRank、中心度等。

3. GNN训练管道：输入图$\to$GNN网络层迭代$\to$得到节点嵌入（或每个节点的隐层表示）$\to$得到预测头（prediction head，节点级别、边级别、图级别的任务涉及不同的预测头，通常都由节点嵌入通过运算得到）$\to$得到预测结果$\to$评估指标与损失函数。

4. 节点级别的预测头：直接$\text{Head}(z_u)=W{z}_u$（节点嵌入输入到一个全连接层）

5. 边级别的预测头：$\text{Head}(z_u,z_v)$，简单的方法就是拼起来然后输入到全连接层，即$\text{Linear}(\text{Concat}(\cdot ,\cdot ))$，也可以取点积$z_u^{\top }{z}_v$（这个只能输出一个标量），或是二次型$z_u^{\top }W{z}_v$（这个可以多用几个不同的$W$，将得到的标量结果拼起来，得到的是一个向量）

6. 图级别的预测头：这个就与GNN网络层中的$\text{AGG}$函数没什么两样了，取均值，最大值，求和等等。

7. 层级图池化（hierarchical global pooling）：

   直接对所有节点嵌入的每一维进行池化是不合理的，这样嵌入的每一维都容易损失很多信息，因此可以两个两个进行池化，这样就少损失一些。

   举个例子，对所有数字进行求和池化： Sum ( { − 1 , − 2 , 0 , 1 , 2 } ) = 0 text{Sum}({-1,-2,0,1,2})=0 Sum({−1,−2,0,1,2})=0， Sum ( { − 10 , − 20 , 0 , 10 , 20 } ) = 0 text{Sum}({-10,-20,0,10,20})=0 Sum({−10,−20,0,10,20})=0，这两个就没有区别了，但是两个两个使用$\text{ReLU}(\text{Sum}(\cdot ,\cdot ))$来池化，就很不一样了。

8. 图划分：用于划分训练集，验证集和测试集，对于那种很大的图上的分类问题，一般就是随机采样节点得到子图作为验证集和测试集，剩下的大部分节点构成的子图作为训练集（注意这种做法要多随机划分几次，报告不同随机种子下的训练情况），这种配置称为是Inductive的。

   注意只用子图可能也会影响图结构，因此有时候会选择Transductive的配置，即训练、验证都用全图，只不过训练时只计算训练集中节点或边的计算损失函数，验证时用验证集中节点或边的标签计算评估指标。

---

GIN

[ICLR 2019]

图同形网络（graph isomorphsim network）：
$${\text{MLP}}_{\Phi }\left(\sum _{x\in S}{\text{MLP}}_f(x)\right)$$
GIN的近邻聚合函数是单射（injective），GIN是目前最具有区分度的GNN（消息传递类型的GNN）！

GCN和GraphSAGE的聚合函数可能会将不同的multi-set输入映射成同样的输出，因此不是那么具有区分度，理想的那种将multi-set输入进行单射的函数应当形如：
$$\Phi \left(\sum _{x\in S}f(x)\right)$$
其中$\Phi$和$f$都是非线性函数，$S$是multi-set输入（比如所有近邻的信息）。

记得前文提过的那个重染色法的$\text{Hash}$函数就是一个单射，GIN相当于是用神经网络来模拟单射的$\text{Hash}$函数：
c ( k + 1 ) ( v ) = Hash ( c ( k ) ( v ) , { c ( k ) ( u ) } u ∈ N ( v ) ) c^{(k+1)}(v)=text{Hash}(c^{(k)}(v),{c^{(k)}(u)}_{uin N(v)}) c(k+1)(v)=Hash(c(k)(v),{c(k)(u)}u∈N(v)​)
建模即为：
$${\text{MLP}}_{\Phi }\left((1+ϵ)\cdot {\text{MLP}}_f(c^{(k)}(v))+\sum _{u\in N(v)}{\text{MLP}}_f(c^{(k)}(u))\right)$$
上面这种单射提升的是GNN的expressive power

---

异构图

异构$G=(V,E,R,T)$：

1. $v_i\in V$
2. $(v_i,r,v_j)\in E$，带关系的边
3. 节点类型：$T(v_i)$
4. 关系类型$r\in R$

---

RGCN

即关系型图卷积网络（Relational GCN），图的边上带有关系标签：
$$h_v^{(l+1)}=\sigma \left(\sum _{r\in R}\sum _{u\in N_v^r}\frac{1}{c_{v,r}}{W}_r^{(l)}{h}_u^{(l)}+W_o^{(l)}{h}_v^{(l)}\right)$$
其中$c_{v,r}=|N_v^r|$，即以关系$r$连接的邻接点数量。同样上式符合消息生成与消息聚合的形式。

每个关系$r$对应$L$个矩阵（网络共有$L$层）：$W_r^{(1)},...,W_r^{(L)}$，其中$W_r^{(l)}\in d^{(l+1)}\times d^{(l)}$

一般来说，需要对$W_r^{(l)}$进行贵正则化，比如令$W_r^{(l)}$是对角块矩阵，或是令$W_r={\sum }_{b=1}^B{a}_{rb}\cdot V_b$，其中$V_b$是所有关系共用的一个矩阵（基础矩阵）。

1. RGCN用于链接预测：

   ① 首先RGCN对训练监督的边$(E,r_3,A)$进行评分

   ② 构建一个负边（negative edge，即加一条假边）$(E,r_3,B)$

   ③ RGCN对负边进行评分

   ④ 目标函数包括最大化训练监督的边的得分和最小化负边的得分：
   $$l=-\log \sigma (f_{r_3}(h_E,h_A))-\log (1-\sigma (f_{r_3}(h_E,h_B)))$$

---

知识表示学习

知识图谱中关系类型：

1. 对称关系（家人，室友）：来回的关系一样；
2. 互逆关系（导师，学生）：来回的关系不一样；
3. 复合关系（妈妈的爸爸是公公）：关系叠加；
4. 一对多关系（老师有多个学生）：$(h,r)$指向多个$t$
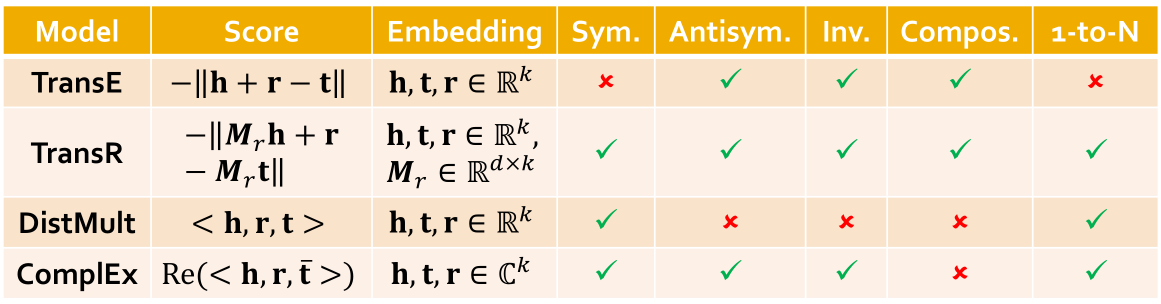
5. 反对称（antisymmetric）关系：上位词（hypernym）和下位词，$r(h,t)\Rightarrow \text{not }r(t,h)$，注意TransE可以建模反对称关系，即$h+r=t,t+r\ne h$

得分函数：

1. 翻译类型的得分函数：$f_r(h,r)=-\Vert h+r-t{\Vert }_{\ast }$

2. TransE：

   

   TransE可以建模互逆关系，复合关系，反对称关系，但无法建模对称关系和一对多关系。

   训练的损失函数：
   $$\mathcal{L}=\sum _{(h,r,t)\in G,(h,r,t^{\prime })\notin G}[\gamma +f_r(h,t)-f_r(h,t^{\prime }){]}_{+}$$

3. TransR：建模实体在空间${\mathbb{R}}^d$中，关系在空间${\mathbb{R}}^k$中，再来一个投影矩阵$M_r\in {\mathbb{R}}^{k\times d}$（从实体空间映射到关系空间）。

   ① $h_{\perp }=M_{r}h,t_{\perp }=M_{r}t$，

   ② $f_r(h,r)=-\Vert h_{\perp }+r-t_{\perp }{\Vert }_{\ast }$

   此时TransR可以建模对称关系，反对称关系，一对多关系互逆关系，复合关系。

4. DistMult：$f_r(h,t)={\sum }_i{h}_i{r}_i{t}_i$，即为连乘求和。

   可以建模一对多关系，对称关系，不能建模反对称关系，互逆关系，复合关系。

5. ComplEx：$f_r(h,t)=\text{Re}({\sum }_i{h}_i{r}_i{\bar{t}}_i)$，$\text{Re}$表示取实部。

   其中向量是在${\mathcal{C}}^k$中建模，即是复数嵌入向量，${\bar{t}}_i$是共轭复数。

   可以建模一对多关系，对称关系，反对称关系（使用），互逆关系，但不能建模复合关系。

   关于对称关系的推导：
   $$f_r(h,t)=\text{Re}\left(\sum _i{h}_i{r}_i{\bar{t}}_i\right)=\sum _i\text{Re}(r_i{h}_i{\bar{t}}_i)=\sum _i{r}_i\cdot \text{Re}(h_i\cdot {\bar{t}}_i)=\sum _i{r}_i\cdot \text{Re}({\bar{h}}_i{t}_i)=\sum _i\text{Re}(r_i{\bar{h}}_i{t}_i)=f_r(t,h)$$

---

知识图谱与多级推理

1. 知识图谱中的查询类型：

   ① 一级（one-hop）查询：$A\stackrel{r}{\to }B$

   ② 路径查询：$A\stackrel{r_1}{\to }B\stackrel{r_2}{\to }C$（这种就是多级推理）

   ③ 联合（conjunctive）查询：$A\stackrel{r_1}{\to }C\stackrel{r_2}{\leftarrow }B$

   举个联合查询的例子：什么药物能够治疗乳腺癌并且引发头痛？

   理想情况下，如果知识图谱足够完备，那么直接通过逻辑搜索即可解决查询问题，然而实际上知识图谱永远不可能是完整的（随着时间需要更新，人工编纂也必然遗漏信息）。

2. 知识图谱补全（KGC）：

   遍历知识图谱中长度为$L$路径的时间复杂度为$O(d_{\max }^L)$，其中$d_{\max }$为节点最大度数。

   但是我们可以在向量空间中遍历知识图谱的所有关系和节点！

   比如给定一级查询$(h,r)$，预测目标为$q=h+r$，然后找个与$q$最相近的$t$即可。

   多级查询$(h,r_1,r_2,...)$同理，联合查询等价于$(h_1,r_1,h_2,r_2)$，那就是要找一个$t$与$h_1+r_1$和$h_2+r_2$都接近（下面会告诉你具体怎么做）。

   这种查询的思想也可以用于KGC。

3. 盒嵌入（box embeddings）：

   可能有人注意到联合查询其实是不容易处理的，如果节点嵌入和关系嵌入学得不好，可能$h_1+r_1$与$h_2+r_2$差的很远，而且理论上$h_1+r_1$应该对应很多实体，$h_2+r_2$也对应很多实体，我们要做的是在这两个集合的实体取交集。

   因此可以考虑使用盒嵌入，即一类实体的嵌入（在超空间中就是一个超矩形的区域）：
   $$\mathbf{q}=(\text{center}(q),\text{offset}(q))$$
   记录这块超矩形区域的中心和边界即可，然后联合查询就化简为超矩形取交集（应该也是一块超矩形），最后的目标就是找一个实体$t$，使得它与这块超矩形交集距离最近（需要定义点到空间的距离）。

   具体而言，关于盒嵌入有很多不同的做法，这里只举一种可行的做法：

   ① 实体嵌入都是向量，但关系嵌入是盒嵌入

   ② 那么$h+r$就映射到了一块盒空间：
   $$\begin{gathered} \text{center}(q^{\prime })=\text{center}(q)+\text{center}(r) \\ \text{offset}(q^{\prime })=\text{offset}(q)+\text{offset}(r) \end{gathered}$$
   ③ 然后若干盒子的交集还是一个盒子（具体需要用神经网络训练这种映射）：
   $$\begin{gathered} \text{center}(q_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}})=\sum _i{w}_i\odot \text{center}(q_i) \\ {w}_i=\frac{\exp (f_{\mathrm{c}\mathrm{e}\mathrm{n}}(\text{center}(q_i)))}{{\sum }_j\exp (f_{\text{cen}}(\text{center}(q_j)))} \\ \text{center}(q_i)\in {\mathbb{R}}^d,w_i\in {\mathbb{R}}^d \\ \text{offset}(q_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}})=\min (\text{offset}(q_1),...,\text{offset}(q_n))\odot \sigma (f_{\mathrm{o}\mathrm{f}\mathrm{f}})(\text{offset}(q_1),...\text{offset}(q_n))) \\ \begin{array}{rl}\text{where}:& \odot \text{ is hadamard product(element-wise product)}\\ & f_{cen}\text{ and }{f}_{\mathrm{o}\mathrm{f}\mathrm{f}}\text{ is neural networks}\\ & w_i\text{ is self-attention score}\end{array} \end{gathered}$$
   ④ 关于点到盒子的距离：
   $$d_{\text{box}}(\mathbf{q},v)=d_{\mathrm{o}\mathrm{u}\mathrm{t}}(\mathbf{q},v)+\alpha d_{\mathrm{i}\mathrm{n}}(\mathbf{q},v)$$
   其中$d_{\mathrm{o}\mathrm{u}\mathrm{t}}$是点$v$到盒子$\mathbf{q}$边界的最短距离，然后$d_{\mathrm{i}\mathrm{n}}$是从边界位置到盒子$\mathbf{q}$中心的最短距离。$0<\alpha <1$是正则系数。

4. 与或查询（AND-OR queries）：

   上面这种联合查询是交集，即是与查询，那么还可能有取并集，即或查询。

   注意在二维平面上，三个节点$v_1,v_2,v_3$构成锐角三角形时，我们总是可以两两画出盒子将两个点框起来而不框进第三个点，但是如果是钝角三角形，就无法满足这种情况了，推广到高维空间亦是如此。因此或查询要更加复杂。

   结论是：对于任意$M$个联合查询$q_1,...,q_M$以及互不覆盖（non-overlapping）的答案，我们需要$\Theta (M)$维的空间才能处理所有的或查询。

   那么既然做与或查询这么困难，实际方法是先分别查询，然后在最后一步再取并集。

5. 查询到盒子（query2box）的训练方法：

   ① 从训练图$G_{\text{train}}$中随机采样一个查询$q$，以及答案$v\in [q{]}_{G_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}}$，以及一个负样本$v^{\prime }\notin [q{]}_{G_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}}$

   ② 嵌入查询$q$

   ③ 计算$f_q(v)$与$f_q(v^{\prime })$

   ④ 最优化损失函数$l$（最大化$f_q(v)$并最小化$f_q(v^{\prime })$）：
   $$l=-\log \sigma (f_q(v))-\log (1-\sigma (f_q(v^{\prime })))$$

---

子图与Motif

motif好像就是节点导出子图（induced subgraph），主要是用于刻画图的局部特征，motif可以视为图的一个子结构，这种子结构可能在图中有多次出现。

关于motif的几个指标

1. $Z\text{-score}$：$Z_i$用于刻画motif i的统计显著性
   $$Z_i=\frac{N_i^{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}}-{\bar{N}}_i^{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}}{\text{std}(N_i^{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}})}$$
   其中$N_i^{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}}$是图中motif i出现的次数，${\bar{N}}_i^{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}$是在随机生成的图中motif i出现的平均次数

2. 网络显著性（network significance profile）：
   $$S{P}_i=\frac{Z_i}{\sqrt{{\sum }_j{Z}_j^2}}$$

总的来说，图越大，$Z\text{-score}$越高。

我们很多时候是想要在图中挖掘出出现频次很高的motif，有点类似数据挖掘里的频繁项集，但是寻找频繁motif是一个NP-hard的问题。

跟下面的神经子图匹配一样，也有通过神经方法来解决这个频繁motif挖掘的问题（但是我还是每太看懂，这两个的方法其实是很接近的，但是就是看不明白）。

---

神经子图匹配（没有看懂）

神经子图匹配（Neural subgraph matching）问题定义：给一个整图$G$和一个小图$g$，判断$g$是否是$G$的子图？

这个问题其实很复杂（要逐点逐边进行对比，显然是NP-hard），但我们可以使用神经网络的方法来解决（这倒是很新奇）。

思想是通过节点嵌入进行对比，但是原理每太看明白，感觉有点奇特。

推荐一篇其他人写的这章slide的博客，里面稍微记了一些笔记内容，但是不多，还是不太搞得明白。

---

推荐系统

问题抽象：给定用户与商品之间的交互信息，需要预测用户在将来会与哪些商品进行交互，这可以视为是链接预测问题。

TopK推荐：给每个用户至多推荐$K$个商品，评估指标是Recall@K，即推荐的$K$个商品中，正确的商品数占用户真实将来交互的商品数的比例（$|P_u\cap R_u|/|P_u|$）

1. 基于嵌入的模型：定义$U$是用户集合，$V$是商品集合，$E$是交互边

   旨在计算$\text{score}(u,v)$，那么就是计算两个节点嵌入的相似度$f_{\theta }(u,v)$：
   $$\mathcal{L}=-\frac{1}{|E|}\sum _{(u,v)\in E}\log (\sigma (f_{\theta }(u,v)))-\frac{1}{|E_{\mathrm{n}\mathrm{e}\mathrm{g}}|}\sum _{(u,v)\in E_{\mathrm{n}\mathrm{e}\mathrm{g}}}\log (1-\sigma (f_{\theta }(u,v)))$$
   注意这种损失函数（称为Binary Loss）是非个性化的（non-personalized），因为所有正边和负边都是对于所有用户生效的，但是评价指标Recall@K是个性化的（要根据每个用户的$P_u$来定）。

   因此提出贝叶斯个性化排行损失：
   $$\mathcal{L}(u^{\ast })=\frac{1}{|E|\cdot |E_{\mathrm{n}\mathrm{e}\mathrm{g}}|}\sum _{(u^{\ast },v_{\mathrm{p}\mathrm{o}\mathrm{s}})\in E(u^{\ast })}\sum _{(u^{\ast },v_{\mathrm{n}\mathrm{e}\mathrm{g}})\in E_{\mathrm{n}\mathrm{e}\mathrm{g}}(u^{\ast })}-\log (\sigma (f_{\theta }(u^{\ast },v_{\mathrm{p}\mathrm{o}\mathrm{s}})-f_{\theta }(u^{\ast },v_{\mathrm{n}\mathrm{e}\mathrm{g}})))$$
   总的损失函数定义为：
   $$\mathcal{L}=\frac{1}{|U|}\sum _{u^{\ast }\in U}\mathcal{L}(u^{\ast })$$

2. 基于GNN的模型：

   • [Wang et al. 2019] Neural Graph Collaborative Filtering (NGCF)

     协同过滤的神经版本，根据节点的嵌入来做的协同过滤。

   • [He et al. 2020] LightGCN

     这个后面有一个章节（LightGCN概述）是讲这个网络的原理的，这里不赘述。不过这里的slide讲得好像更详细一些。其实本质上还是用的用户嵌入和商品嵌入计算得分函数。

     LightGCN里聚合就是简单的等权平均。

   • PinSAGE [Ying et al. 2018]

     这个是用于图像处理的GNN，是目前GCN最大的工业应用。

---

Louvain算法

Louvain算法是基于模块度的社区发现算法，该算法在效率和效果上都表现较好，并且能够发现层次性的社区结构，其优化目标是最大化整个社区网络的模块度。

---

GraphRNN

转载自https://zhuanlan.zhihu.com/p/272854914

图由若干个点和边构成，一个很自然的想法是，逐个生成这些点和边，也就是生成节点和连边的序列，这正是RNN擅长的事，所以有了GraphRNN模型。

下图是一个GraphRNN的示意图，$S_i^{\pi }$表示序列每一步生成的元素，与传统RNN不同的是，GraphRNN每一步不仅要生成节点，还要生成这个节点与其他节点之间的连边，而要生成若干个连边，需要另一个序列生成模型，所以GraphRNN生成的序列S是一个Seq of Seq，即，序列的序列，这也正是GraphRNN复杂的地方。

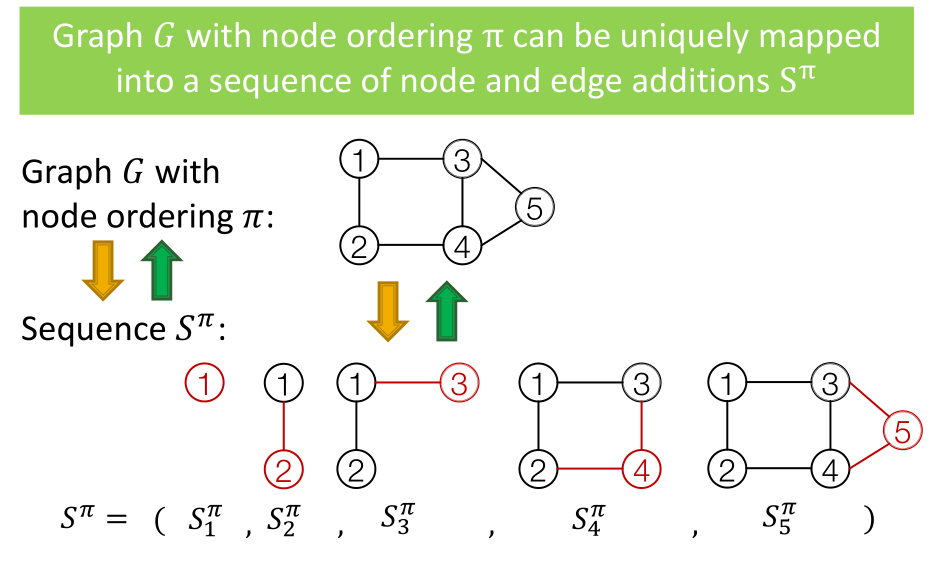
下面来看一个GraphRNN的示例，第一个unit是序列的其实状态，第二个unit生成了1号节点，然后生成了下一个节点与1号节点的连边关系，值是1，因此第三个unit生成了节点2，并且节点2与节点1相连，然后生成下一个节点与节点1和2的连边，即图中的$S_3^{\pi }$，节点3和节点1连接，与节点2不连接，由此到下一个unit，生成了节点3，剩余unit可以以此类推。这里，Node-level的RNN只负责生成Edge-level RNN的初始状态，Edge-level RNN负责生成连边关系。

课程中还提到，训练时采用Teacher Forcing方式，即，下一个unit的输入不来自上一个unit的输出，而是上一个unit的label，这就保证了GraphRNN一定可以生成一张一模一样的图，但是这种过拟合的方法在实践中是否管用，笔者持保留意见。

---

一些前沿研究

1. 位置感知（position-aware）的GNN：

   相对概念的结构感知的图，结构感知的图会将图中的等价节点标注为一类（可以看Graphlet的那个图里，只标注的同类节点，未标注的其他节点在结构上都有同等的对应），位置感知的图则有点类似聚类的标注，比如同属于一个三角形的三个顶点会标为一类，另一个三角形的三个节点标为另一类。

   GNN总是会在位置感知的任务上失败，因为GNN对位置并不敏感。

   因此需要引入一个锚定点（Anchor），随机选取即可，以相对于锚定点的距离来判定不同节点的位置。

   类似有推广到锚定集合，即选一群点作为锚定。

   基于此可以训练得到带有位置信息的节点嵌入和边嵌入。

2. 身份感知（identity-aware）的GNN：

   这个考虑的问题是，在一些情况下，输入不同的图，但是它们的计算图是完全相同的。

   这个问题感觉偏理论计算机研究的领域，由此衍生出的概念是ID-GNN

   看到这里越来越觉得GNN真的没有看起来那么简单，相比于神经网络，GNN有更多需要发掘的理论问题，根源就是图论的复杂性，很多图论问题都可以拉到GNN里来考虑。

3. GNN的鲁棒性（robustness）：即对图做微扰，预测结果发生的变化。

---

LightGCN概述

[Wu et al. ICML 2019]，从原先的GCN模型中去除了非线性激活层。

数学标记定义：

1. 邻接矩阵$A$，这里做了一个自循环处理，即$A\leftarrow A+I$，这个在GCN里也是这么处理的；
2. 节点度数矩阵$D$
3. 正则化的邻接矩阵$\tilde{A}=D^{-1/2}A{D}^{-1/2}$
4. $E^{(k)}$表示第$k$层的嵌入矩阵；
5. $E$表示输入的嵌入矩阵；
6. $E^{(k+1)}=\text{ReLU}(\tilde{A}{E}^{(k)}{W}^{(k)})$，$W^{(k)}$为可学习得到参数；

---

最后

以上就是土豪金针菇为你收集整理的【学习笔记】CS224W速记（图模型专题）序言的全部内容，希望文章能够帮你解决【学习笔记】CS224W速记（图模型专题）序言所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。