参考:MATLAB Function Reference 菜鸟学概率统计——高斯分布
问题说明:已知变量服从高斯分布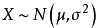
1.求解高斯分布的概率:已知门值变量gate的值,已知变量X>gate的概率。
2.高斯分布的分布概率反解:已知X>gate的概率pd,求解 门值变量gate。
解决方法:使用MATLAB程序仿真求解上述问题,使用的函数是Matlab自带的Error functions,有以下几种函数:
Syntax
Y = erf(X)
Error function
Y = erfc(X)
Complementary error function
Y = erfcx(X)
Scaled complementary error function
X = erfinv(Y)
Inverse error function
X = erfcinv(Y)
Inverse complementary error function函数说明:
The error function erf(X) is twice the integral of the Gaussian distribution with 0 mean and variance of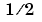 .
.
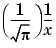
程序仿真求解上述问题概括:当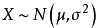
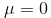
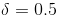
erf(X)函数表示:X变量在(0,X)区域分布概率的两倍。当X>0时,就是(-X,X)区域内的分布概率。
erfc(X)函数表示:X变量在(X,inf)区域内分布概率的两倍。其中inf表示正无穷
erfinv(Y)表示:erf(X)的函数反函数,Y=erf(X),已知Y的值求解X的值。
erfcinv(Y):erfcinv(X)函数的反函数,与上述同理。
求解一般高斯分布的分布概率: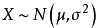
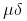
1.已知分布概率为Y,求解X
2.已知X,求解分布概率Y
(2)Matlab 如何生成服从高斯分布(正态分布)的随机数
使用randn函数生成:randn 标准正态分布
如果你想变成你的需要的均值和方差的话:a+b*randn,均值是a,标准差是b。
如果你想产生很多,比如一个1000*1的向量,那么在randn后边加括号,写上尺寸就行了 randn([1000,1])。
最后
以上就是谨慎小蝴蝶最近收集整理的关于Matlab求解高斯分布的概率以及概率反解-使用erf相关函数的全部内容,更多相关Matlab求解高斯分布内容请搜索靠谱客的其他文章。
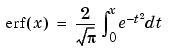
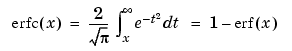
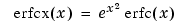
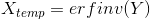
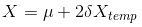
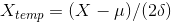
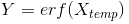








发表评论 取消回复