例题：Abbott的复仇（UVa 816）

有一个最多包含9*9个交叉点的迷宫。输入起点、离开起点时的朝向和终点，求一条最短路（多解时任意输出一个即可）

这个迷宫的特殊之处在于：进入一个交叉点的方向（用NEWS这四个字母分别表示北东西南，即上下左右）不同，允许出去的方向也不同。例如，12 WLF NR ER*表示交叉点（1,2）（上数第一行，左数第二列）有3个路标（字符“*”只是结束标志），如果进入交叉点时的朝向为W（即朝左），则可以左转（L）或者直行（F）；如果进入时朝向为N或者E则只能右转（R），如图所示：

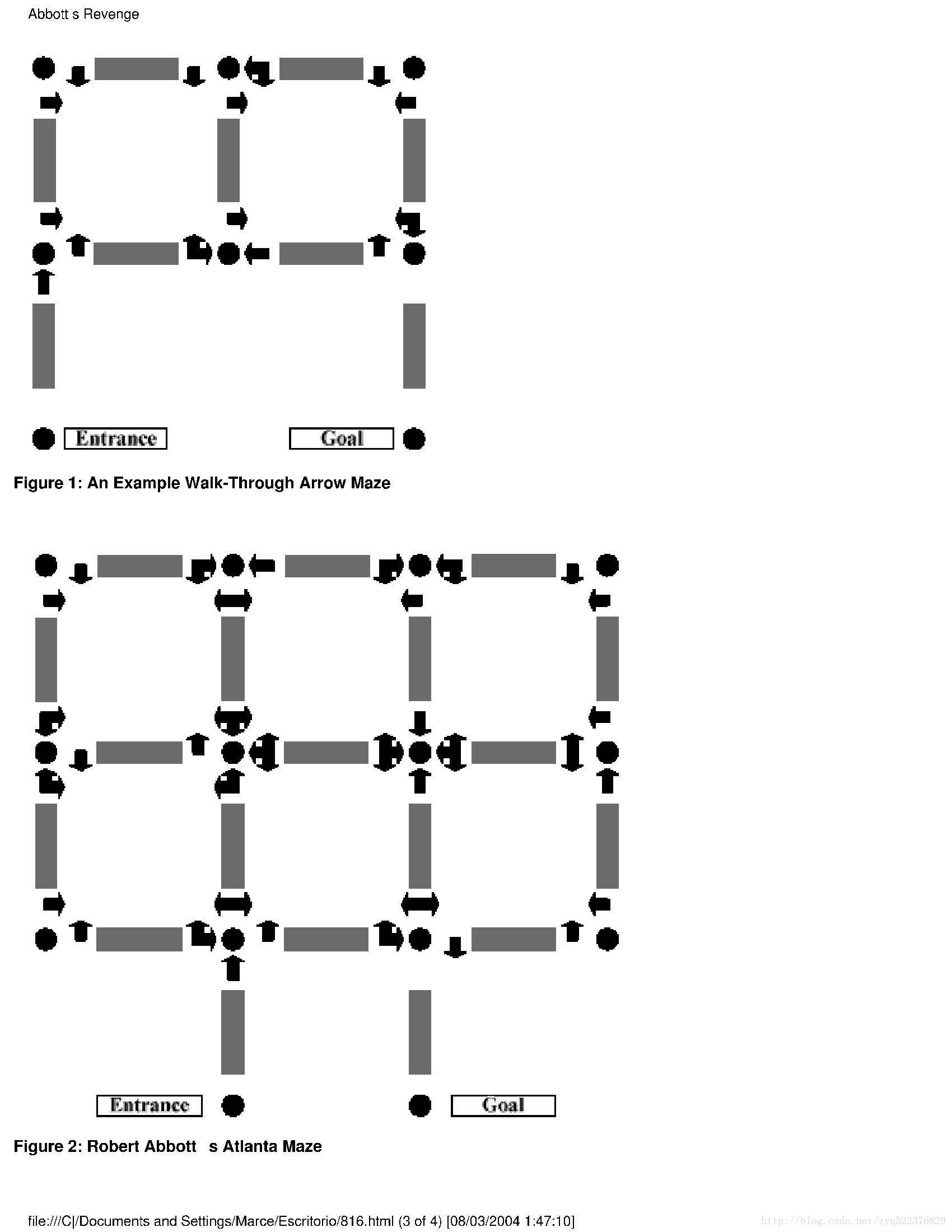
【分析】

本题和普通的迷宫在本质上是一样的，但是由于“朝向”也起到了关键作用，所以需要用一个三元组（r,c,dir）表示位于（r,c），面朝dir这个状态。假设入口位置为（r0,c0），朝向为dir，则初始状态并不是（r0,c0,dir），而是（r1,c1,dir），其中，（r1,c1）是（r0,c0）沿着方向dir走一步之后的坐标。此处用d[r][c][dir]表示初始状态到（r,c,dir）的最短路长度，并且p[r][c][dir]保存了状态（r,c,dir）在BFS树中的父节点

【代码】

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cctype>
#include <cstring>
#include <string>
#include <sstream>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
#include <stack>
#include <queue>

using namespace std;

const int maxn = 10;

struct Node
{
	int r, c, dir; // 走到(r,c)时的朝向dir，N~0,E~1,S~2,W~3
	Node(int r = 0, int c = 0, int dir = 0) :r(r), c(c), dir(dir) {}
};

const char* dirs = "NESW"; // 顺时针
const char* turns = "FLR";

int dirID(char c) {
	return strchr(dirs, c) - dirs;
} // 把方向字符转化为0~3，分别对应NESW

int turnID(char c) {
	return strchr(turns, c) - turns;
} // 把转向字符转化为0~2，分别对应FLR

int hasEdge[maxn][maxn][4][3]; // 表示当前状态是(r,c,dir)是否可以沿着转向turn行走
int d[maxn][maxn][4];
Node p[maxn][maxn][4];
int r0, c0, dir, r1, c1, r2, c2;

const int dr[] = { -1, 0, 1, 0 };
const int dc[] = { 0, 1, 0, -1 };

Node walk(const Node& u, int turn) {
	int dir = u.dir;
	if (turn == 1) {
		dir = (dir + 3) % 4; // 逆时针左转
	}
	else if (turn == 2) {
		dir = (dir + 1) % 4; // 顺时针右转
	}
	return Node(u.r + dr[dir], u.c + dc[dir], dir);
}

bool inside(int r, int c) { // 是否出界
	return r >= 1 && r <= 9 && c >= 1 && c <= 9;
}

bool readCase() // 读取数据
{
	char s[99], s2[99];
	scanf("%s", s);
	char errs[99] = "END";
	if (strlen(s) == 3 && s[0] == 'E' && s[1] == 'N' && s[2] == 'D') {
		return false;
	}
	scanf("%d%d%s%d%d", &r0, &c0, s2, &r2, &c2);

	printf("%sn", s);

	dir = dirID(s2[0]);
	r1 = r0 + dr[dir];
	c1 = c0 + dc[dir];

	memset(hasEdge, 0, sizeof(hasEdge));
	while (1) {
		int r, c;
		scanf("%d", &r);
		if (r == 0) {
			break;
		}
		scanf("%d", &c);
		while (scanf("%s", s) == 1 && s[0] != '*') {
			for (int i = 1; i < strlen(s); i++) {
				hasEdge[r][c][dirID(s[0])][turnID(s[i])] = 1;
			}
		}
	}
	return true;
}

void printAns(Node u) // 打印最短路
{
	vector<Node> nodes;

	while (1) {
		nodes.push_back(u);
		if (d[u.r][u.c][u.dir] == 0) {
			break;
		}
		u = p[u.r][u.c][u.dir];
	}
	nodes.push_back(Node(r0, c0, dir));

	int cnt = 0;
	for (int i = nodes.size() - 1; i >= 0; i--) {
		if (cnt % 10 == 0) {
			printf(" ");
		}
		printf(" (%d,%d)", nodes[i].r, nodes[i].c);
		if (++cnt % 10 == 0) {
			printf("n");
		}
	}
	if (nodes.size() % 10 != 0) {
		printf("n");
	}
}

void solve()//建立BFS树
{
	queue<Node> q;
	memset(d, -1, sizeof(d));
	Node u(r1, c1, dir);
	d[u.r][u.c][u.dir] = 0;
	q.push(u);
	while (!q.empty()) {
		Node u = q.front();
		q.pop();
		if (u.r == r2 && u.c == c2) { // 终点
			printAns(u);
			return;
		}
		for (int i = 0; i < 3; i++) {
			Node v = walk(u, i);
			if (hasEdge[u.r][u.c][u.dir][i] &&
				inside(v.r, v.c) && 
				d[v.r][v.c][v.dir] < 0) {
				d[v.r][v.c][v.dir] = d[u.r][u.c][u.dir] + 1;
				p[v.r][v.c][v.dir] = u;
				q.push(v);
			}
		}
	}
	printf("  No Solution Possiblen");
}

int main()
{
	while (readCase()) {
		solve();
	}

	return 0;
}

最后

以上就是顺心铃铛为你收集整理的例题：Abbott的复仇（UVa 816）的全部内容，希望文章能够帮你解决例题：Abbott的复仇（UVa 816）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。