雷达系统仿真——线性调频信号的仿真

66 阅读 0 评论 44 点赞

我是靠谱客的博主柔弱墨镜，最近开发中收集的这篇文章主要介绍雷达系统仿真——线性调频信号的仿真，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1 线性调频（LFM）信号的优点

雷达原理中学过，增大脉宽，就增加了发射信号的功率，意味着增加了目标的探测能力（探测距离）；相对的，减少脉宽，可以增加雷达的距离分辨力。

对常规矩形脉冲雷达来说，发射的脉冲信号和回波的脉宽是一样的，因此，雷达的距离分辨力和探测距离之间成反比关系。

脉冲压缩技术用能量累计的技术，使得接收回波经过处理后的脉宽比发射脉冲大大减小。在脉冲压缩中经常使用的是线性调频脉冲信号。

2 线性调频脉冲信号定义

瞬时频率线性增加的线性调频脉冲波形的复包络为：

$e^{j pi(beta / tau) t^{2}}$

其中， $β$ 为信号带宽， $τ$ 为脉宽。

如果用 $θ (t)$ 表示相位，则瞬时频率为：

$1 2 π d Θ ( t ) d t = β τ t frac{1}{2 pi} frac{d Theta(t)}{d t}=frac{beta}{tau} t$

为 $t$ 的线性函数，斜率为 $β / τ$ 。

瞬时频率线性减少的线性调频脉冲波形的复包络为：

$e^{-j pi beta / tauleft(t^{2}-2 tau tright)}$

脉冲压缩波形的时间带宽乘积 $β τ$ 大于1。

3 如何创建线性FM脉冲波形

创建线性FM脉冲波形，要用到matlab phased.LinearFMWaveform。可以自定义波形特征，包括：

采样率（Sample rate）
脉宽（Duration of a single pulse）
脉冲重复频率（Pulse repetition frequency）
扫频带宽（Sweep bandwidth）
扫频方向（Sweep direction）（up或down），对应瞬时频率的增加和减少
包络（Envelope）, 描述了脉冲的幅度调制，包络可以是矩形的（rectangular）或是高斯的（Gaussian）。

矩形包络如下所示，其， $τ$ 为脉宽：

$\ 0 & text { otherwise }end{array}right.$

高斯包络如下所示：

$a(t)=e^{-t^{2} / tau^{2}} quad t geq 0$

每个波形的采样点数或是脉冲数

4 创建LFM脉冲波形

下面的例子演示如何用phased.LinearFMWaveform来创建一个LFM脉冲波形，并且对波形的参数进行设置。

下面的代码创建一个LFM脉冲，采样频率为 $1 M H z$ ，脉宽为 $50 μ s$ ，瞬时频率随时间增加，扫频带宽 $100 k H z$ ，脉冲重复频率 $10 k H z$ ，幅度调制为矩形。

waveform = phased.LinearFMWaveform('SampleRate',1e6,...
    'PulseWidth',50e-6,'PRF',10e3,...
    'SweepBandwidth',100e3,'SweepDirection','Up',...
    'Envelope','Rectangular',...
    'OutputFormat','Pulses','NumPulses',1);

5 绘制LFM脉冲波形

下面的例子演示了如何绘制LFM脉冲波形。

LFM脉冲脉宽为 $100 μ s$ ，扫频带宽为 $200 k H z$ ，PRF为 $4 k H z$ ，其余参数为默认。计算其时间带宽积，画出实部的波形，画出一整个脉冲重复间隔的波形。

waveform = phased.LinearFMWaveform('PulseWidth',100e-6,...
    'SweepBandwidth',200e3,'PRF',4e3);

在命令窗口打印时间带宽积：

disp(waveform.PulseWidth*waveform.SweepBandwidth)

结果为：

画出实部的时域波形：

plot(waveform)

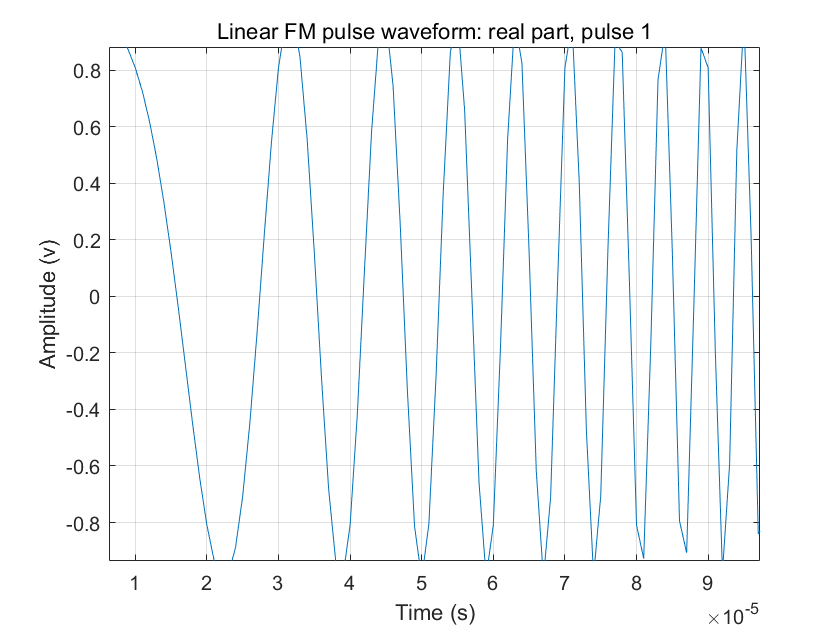
在这里插入图片描述

用step命令来获取一个完整的脉冲重复间隔的数据。画出其实部和虚部。

y = waveform();
t = unigrid(0,1/waveform.SampleRate,1/waveform.PRF,'[)');
figure
subplot(2,1,1)
plot(t,real(y))
axis tight
title('Real Part')
subplot(2,1,2)
plot(t,imag(y))
xlabel('Time (s)')
title('Imaginary Part')
axis tight

结果如下：

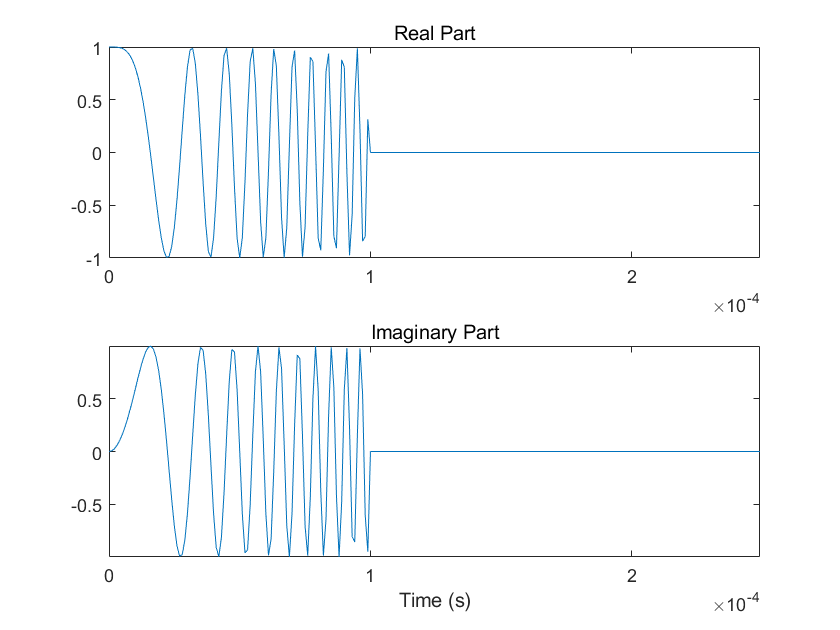
在这里插入图片描述

6 LFM波形的模糊函数

6.1 模糊函数的概念

Ambiguity function，模糊函数。

模糊函数是进行雷达波形设计和分析信号处理系统性能的重要工具，根据雷达信号的模糊函数，可以确定雷达发射波形的分辨能力、测量精度、模糊情况以及抑制干扰的能力。

雷达模糊函数表示匹配滤波器的输出。是回波和发射脉冲的延迟时间 $τ$ 和多普勒频移 $f$ 的二元函数。

雷达模糊函数有多种定义，有的适用于窄带信号，有的适用于宽带信号。对于一个信号 $s (t)$ ，其窄带模糊函数表达式为：

$f)=int_{-infty}^{infty} s(t) s^{*}(t-tau) e^{i 2 pi f t} d t$

注意，在上式中，如果多普勒频移 $f = 0$ ，则上式就是信号的自相关函数。

6.2 LFM的模糊函数的仿真

设置LFM脉冲的参数：

waveform = phased.LinearFMWaveform('PulseWidth',100e-6,...
    'SweepBandwidth',2e5,'PRF',1e3);

生成波形：

wav = waveform();

绘制模糊函数的三维图：

[afmag_lfm,delay_lfm,doppler_lfm] = ambgfun(wav,...
    waveform.SampleRate,waveform.PRF);
surf(delay_lfm*1e6,doppler_lfm/1e3,afmag_lfm,...
    'LineStyle','none')
axis tight
grid on
view([140,35])
colorbar
xlabel('Delay tau (mus)')
ylabel('Doppler f_d (kHz)')
title('Linear FM Pulse Waveform Ambiguity Function')

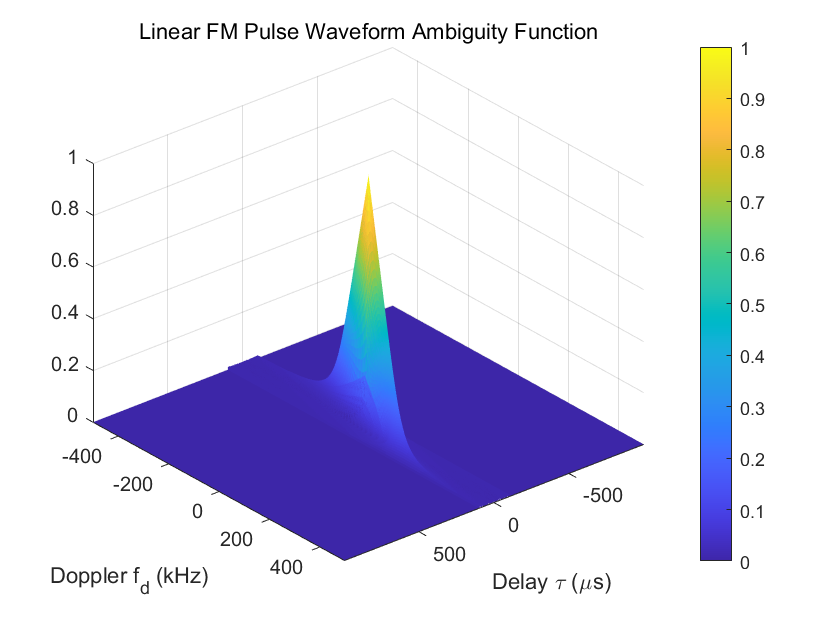
在这里插入图片描述

结果表明，当延迟和多普勒频移为0时，模糊度最低。

7 矩形脉冲和LFM脉冲的自相关结果的比较

下面的例子演示如何计算和绘制矩形和LFM脉冲的模糊函数幅度（ambiguity function magnitudes）。当多普勒频移为0时，模糊函数的输出即为序列的自相关，即脉冲压缩的过程。

创建具有相同PW和PRF的矩形脉冲和LFM脉冲，生成波形：

rectwaveform = phased.RectangularWaveform('PRF',20e3);
lfmwaveform = phased.LinearFMWaveform('PRF',20e3);
xrect = rectwaveform();
xlfm = lfmwaveform();

计算两个波形的模糊函数幅度：

%[afmag,delay] = ambgfun(___,'Cut','Doppler') returns delays from a zero-Doppler cut through the 2-D normalized ambiguity function magnitude.
[ambrect,delay] = ambgfun(xrect,rectwaveform.SampleRate,rectwaveform.PRF,...
    'Cut','Doppler');
ambfm = ambgfun(xlfm,lfmwaveform.SampleRate,lfmwaveform.PRF,...
    'Cut','Doppler');

绘制幅度波形：

subplot(211)
stem(delay,ambrect)
title('Autocorrelation of Rectangular Pulse')
axis([-5e-5 5e-5 0 1])
set(gca,'XTick',1e-5*(-5:5))
subplot(212)
stem(delay,ambfm)
xlabel('Delay (seconds)')
title('Autocorrelation of Linear FM Pulse')
axis([-5e-5 5e-5 0 1])
set(gca,'XTick',1e-5*(-5:5))

结果如下：

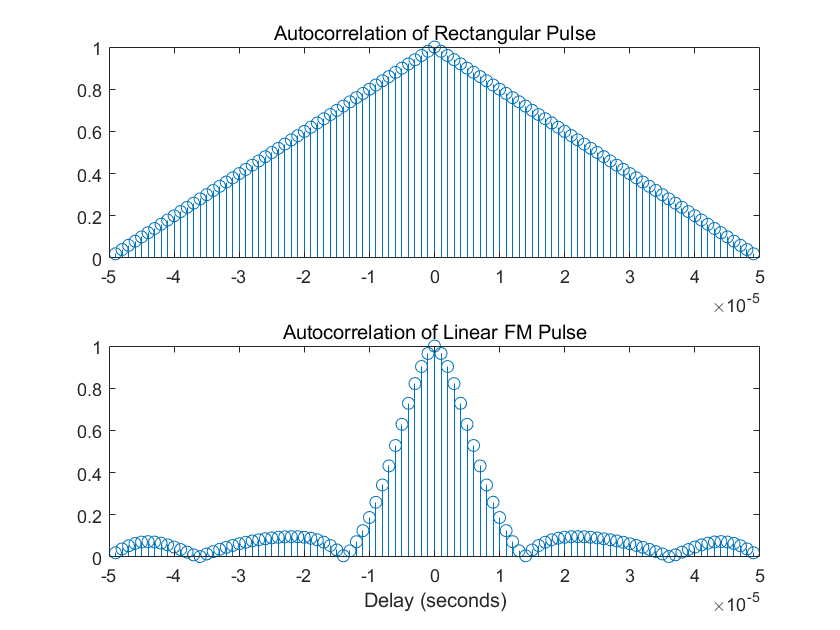
在这里插入图片描述