加扰器的作用
一般来说,数字通信系统的设计及其性能都与所传输的数字信号的统计特性有关。在数字通信设备中,通常从0和1码的交变点提取位定时信息,若经常出现长0或1游程,则将影响位同步的建立和保持。如果数字信号具有周期性,则信号频谱中存在离散谱线。为了限制这种串扰,常要求数字信号的最小周期足够长。
如果我们能够先将信源产生的数字信号变换成具有近似白噪声统计特性的数字序列,再进行传输,这样就可以给数字通信系统的设计和性能估计带来很大方便。
所谓加扰技术,就是不用增加多余度而扰乱信号,改变数字信号统计特性,使其近似于白噪声统计特性的一种技术。这种技术的基础是建立在反馈移存器序列(伪随机序列)的理论基础之上。
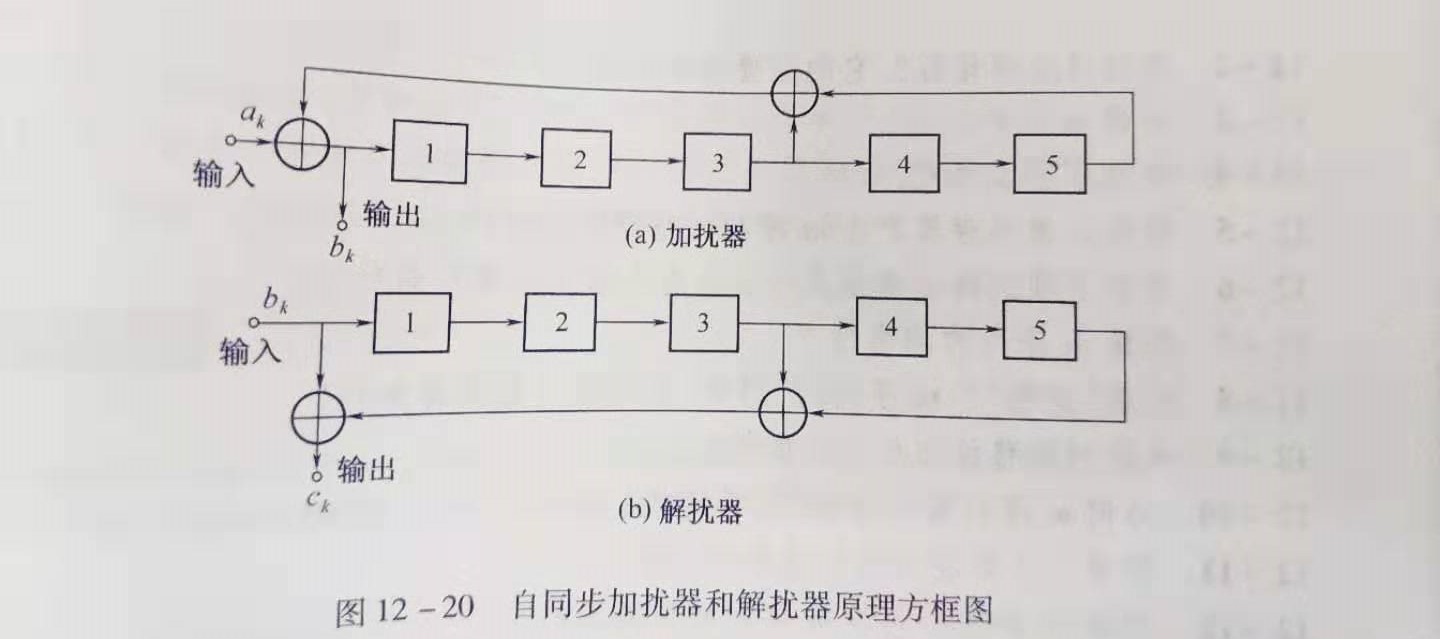
加扰器的原理方框图如下图所示,加扰器的参数主要有生成多项式和移位寄存器初始状态(详见《通信原理(第七版)》-樊昌信)
加扰器与解扰器的Matlab实现
N=100;
x = randi(2,1,N)-1; %原始数据
scrambler = [1,0,1,1,1,0,1]; %加扰器移位寄存器初始状态
descrambler = scrambler; %解扰器移位寄存器初始状态
y_scrambler = zeros(1,N);
subplot(3,1,1)
stairs(x)
axis([0 N -0.2 1.2])
title('原始数据');
%--------------加扰器-----------------%
for i = 1 :N
z = bitxor(scrambler(1),scrambler(4)); %异或
y_scrambler(i) = bitxor(z,x(i));
scrambler=[scrambler(2:7), y_scrambler(i)];
end
subplot(3,1,2)
stairs(y_scrambler)
axis([0 N -0.2 1.2])
title('加扰后的数据');
% ------------ 解扰器 ------------ %
y_descrambler = zeros(1,N);
for i = 1 : N
z = bitxor(descrambler(1),descrambler(4)); %异或
y_descrambler(i) = bitxor(z,y_scrambler(i));
descrambler=[descrambler(2:7), y_scrambler(i)];
end
subplot(3,1,3)
stairs(y_descrambler)
axis([0 N -0.2 1.2])
title('解扰后的数据');
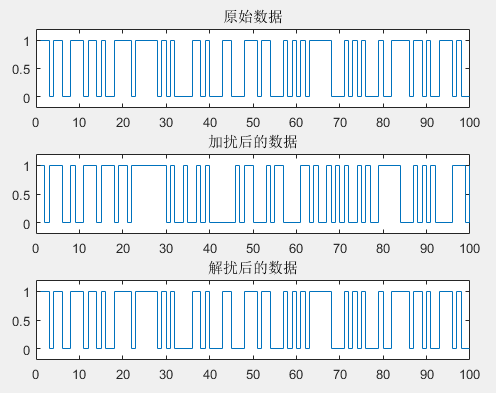
从上图可以看出,解扰后的数据与原始数据相同,证明了程序的正确性。
加扰器与解扰器的FPGA实现
- 加扰器的实现
module scrambler(
input clk,
input din, //输入数据
input rst, //复位信号
input scram_valid, //加扰器使能信号
output reg scram_dout, //加扰器输出
output reg scram_rdy //加扰器输出有效信号
);
parameter scram_seed = 8'b10111010; //寄存器初值
reg[7:1] scrambler=7'b0;
wire temp;
assign temp = din^scrambler[7]^scrambler[4]; //生成多项式S(X)=x^7+x^4+1
always @ (posedge clk )
begin
if (!rst)
begin
scram_rdy <= 0;
scrambler <= scram_seed;
scram_dout <= 0;
end
else
begin
if (scram_valid)
begin
scrambler <= {scrambler[6:1],temp};
scram_rdy <= 1;
scram_dout <= temp;
end
else
begin
scram_rdy <= 0;
scrambler <= scram_seed;
scram_dout <= 0;
end
end
end
endmodule
- 解扰器的实现
module descrambler(
input clk,
input din,
input rst,
input descram_valid, //解扰器使能信号
output reg descram_dout, //解扰器输出
output reg descram_rdy //解扰器输出有效信号
);
parameter descram_seed = 7'b1011101; //寄存器初值
reg[7:1] descrambler;
wire temp;
assign temp = din^descrambler[7]^descrambler[4]; //生成多项式S(X)=x^7+x^4+1
always @ (posedge clk )
begin
if (!rst)
begin
descram_rdy <= 0;
descrambler <= descram_seed;
descram_dout <= 0;
end
else
begin
if (descram_valid)
begin
descrambler <= {descrambler[6:1],din};
descram_rdy <= 1;
descram_dout <= temp;
end
else
begin
descram_rdy <= 0;
descrambler <= descram_seed;
descram_dout <= 0;
end
end
end
endmodule
- Testbench文件
module scrambler_tb;
reg clk=0;
reg reset=1;
reg scram_valid=0;
wire scram_dout;
wire scram_rdy;
`define number 2048
///clk//
always #10 clk = ~clk; // 50MHz 20ns
///reset//
initial
begin
#20 reset=0;
#40 reset=1;
end
reg din;
reg [14:0] cnt=0;
always@(posedge clk)
begin
if (!reset)
begin
scram_valid <= 0;
din <= 0;
end
else
begin
if (cnt <= 15'd10000) //使能信号的周期为10001个时钟周期,有效时长为2048个时钟周期
begin
scram_valid <= 1;
cnt <= cnt + 1'b1;
din <= {$random} % 2; //输入数据为0或1
if (cnt >= `number-1)
begin
scram_valid <= 0;
din <= 0;
end
end
else
begin
scram_valid <= 0;
cnt <= 0;
din <= 0;
end
end
end
scrambler uut(
.clk(clk),
.din(din),
.rst(reset),
.scram_valid(scram_valid),
.scram_dout(scram_dout),
.scram_rdy(scram_rdy)
);
wire descram_dout;
wire descram_rdy;
descrambler uut2(
.clk(clk),
.din(scram_dout),
.rst(reset),
.descram_valid(scram_rdy),
.descram_dout(descram_dout),
.descram_rdy(descram_rdy)
);
endmodule
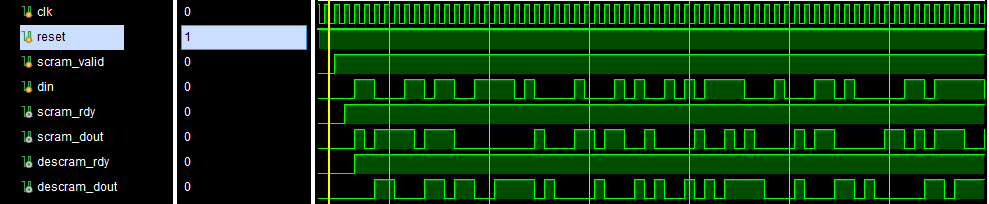
仿真时将加扰器与解扰器进行了级联,仿真结果如下图所示,从图中可以看出,解扰器输出结果(descram_dout)与原始数据(din)相同,仅延迟两个时钟周期,从结果可以看出程序实现了数据的加扰及解扰,结果正确。
最后
以上就是纯真雪糕最近收集整理的关于FPGA中加扰与解扰的实现的全部内容,更多相关FPGA中加扰与解扰内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复