Poisson Blending 实现了非常棒的效果,可以看 《自己动手,实现“你的名字”滤镜》 http://www.cnblogs.com/jsxyhelu/p/7216795.html
它的原理在论文《Poisson Image Editing》中进行了比较详细的阐述,但是英文的大论文看起来的却比较麻烦,在 https://wenku.baidu.com/view/55ac10a7be1e650e53ea9990.html 找到一篇《方轶智_基于泊松方程的图像处理 》,这篇成果中,基本把原论文中关于Poisson Blending(泊松融合)的部分翻译了出来,并且它的综述部分写的相当不错;在http://blog.csdn.net/ZJU_fish1996/article/details/72760571?locationNum=7&fps=1中,作者实现了全文的初略翻译,有一定参考价值。此外,http://eric-yuan.me/poisson-blending/和http://eric-yuan.me/poisson-blending-2/中给出了作者自己的分析和独立的实现。
我在自己将这些资料进行归拢,梳理,并提出自己的思考。首先对几位作者的辛勤工作表示感谢,资料的版权属于它们。
一、Poisson Blending(泊松融合)为什么能够产生如此好的效果
它的基本原理基于人的生物学特性。我们人眼天生就对“突变”更为敏感:比如白纸上的黑线;但是如果这个变化是连续平滑的,那么对人的刺激就要低得多。经过心理学家和计算机科学家的研究,认为二阶偏导数对于解决这个方面的融合问题有帮助,所以才有了我们这里的具体实现。
图像编辑包括全局变化和局部变化,我们关心的是我们所选中的局部区域中如何几乎无缝且无影响地嵌入到目标图像中。传统的工具来完成局部的剪切,是通过克隆工具直接取代那部分区域的内容,因此选择的片区域的改变会导致明显的边缝。所以为了达到我们想要的理想效果,就迫切地需要一种可以消除边缝的且不改变图像其他特征的方法。
这种无缝编辑和克隆方法的核心是数学工具―泊松方程,需满足在所选区域未知函数的拉普拉斯条件,和它的Dirichlct边界条件:未知函数的边界值与目标图像中所选区域的边界值相同。在这两个条件下方程的解是唯一的。首先,心理学家Land和Mccan。在1971年提出通过拉普拉斯算子的限制可以减缓渐变的梯度,当把一幅图像混淆到另一幅图像上几乎注意不到有什么影响。并且,泊松方程可以完成无缝地填满目标图像中的选中区域。
注意,这里的脉络是
1、“提出需要解决的问题” --> 解决无缝融合;
2、“解决问题的方法”-->使用Poisson Blending
3、为什么-->理解并证明Poisson Blending的特性
二、什么是泊松方程,以及它在图像处理这里的运用
粘点百科:
泊松方程为[2]
在这里
 代表的是拉普拉斯算子,而f和
代表的是拉普拉斯算子,而f和
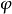 可以是在流形上的实数或复数值的方程。当流形属于欧几里得空间,而拉普拉斯算子通常表示为
可以是在流形上的实数或复数值的方程。当流形属于欧几里得空间,而拉普拉斯算子通常表示为
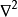 ,因此泊松方程通常写成
,因此泊松方程通常写成
在三维直角坐标系,可以写成
如果有
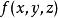 恒等于0,这个方程就会变成一个齐次方程,这个方程称作“拉普拉斯方程”。
恒等于0,这个方程就会变成一个齐次方程,这个方程称作“拉普拉斯方程”。
注意,我们图像处理,一般来说,都是属于欧几里得空间(而不是黎曼几何空间),也是在三维之间坐标系(而不是极坐标系)中的。
在这不多的几行字里面,一再提到了“拉普拉斯方程”。实际上,拉普拉斯方程是泊松方程的齐次表达方式。幸好的是,对于拉普拉斯方程我们要熟悉的多,甚至基本知道它的实现方式。
三、主要算法流程
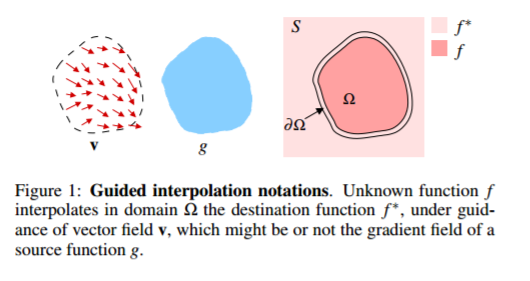
这里的三幅图片分别对应于”前景“”背景“和结果。在原论文中,直接将前景叫做“引导向量域”(我这样理解,使用前景来引导背景的向量)
符号的含义:设图像定义域S为R^2上封闭子集合,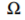 是S的一个封闭子集,它的边界为
是S的一个封闭子集,它的边界为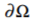 。令f*为定义在S上一个已知的标量函数,代表S减去
。令f*为定义在S上一个已知的标量函数,代表S减去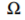 的范围,令f为定义在
的范围,令f为定义在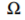 上一个未知的标量函数。最终,令v为定义在
上一个未知的标量函数。最终,令v为定义在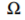 上的向量域。
上的向量域。
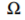 是S的一个封闭子集,它的边界为
是S的一个封闭子集,它的边界为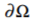 。令f*为定义在S上一个已知的标量函数,代表S减去
。令f*为定义在S上一个已知的标量函数,代表S减去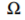 的范围,令f为定义在
的范围,令f为定义在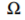 上一个未知的标量函数。最终,令v为定义在
上一个未知的标量函数。最终,令v为定义在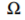 上的向量域。
上的向量域。
定义在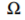 上f*的最简单的插值函数f:最小化问题的插值(在边界是未知等于已知,在内部是梯度变化最小。梯度在二阶偏导为0的时候取极值)
上f*的最简单的插值函数f:最小化问题的插值(在边界是未知等于已知,在内部是梯度变化最小。梯度在二阶偏导为0的时候取极值)
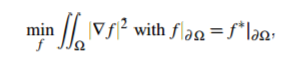 (1)
(1)
其中
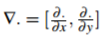 是梯度运算。最小值必须满足相关的拉格朗日方程。
是梯度运算。最小值必须满足相关的拉格朗日方程。
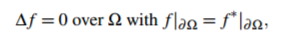 (2)
(2)
其中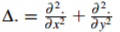 是拉普拉斯算子。
是拉普拉斯算子。
一个引导域是最小化问题(1)的扩展版本中使用的向量域v:(注意 v 是引导向量,也就是前景)
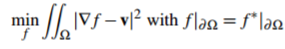 (3)
(3)
它的解是Dirichlet边界条件下泊松方程的唯一解:
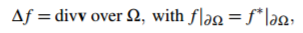 (4)
(4)
其中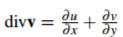 是v= (u,v)的散度。
是v= (u,v)的散度。
一个有用的替代方案是理解泊松插值所做的是定义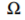 上修正的
上修正的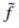 函数,以保证
函数,以保证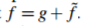 。
。
泊松方程(4)随之成为了以下有边界条件的拉普拉斯方程:
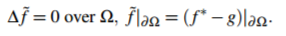 (5)
(5)
因此,在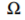 内,我们添加的修正
内,我们添加的修正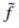 是就是边界
是就是边界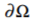 上源和目标错误匹配(f*-g)的一个插值(membrance interpolant)。这一引导插值的特例被用于无缝克隆。
上源和目标错误匹配(f*-g)的一个插值(membrance interpolant)。这一引导插值的特例被用于无缝克隆。
四、简单的例子证明
1-D EXAMPLE 一维的例子,这个可以自己上手计算跟着看,效果非常好
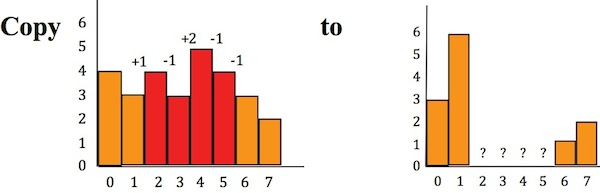
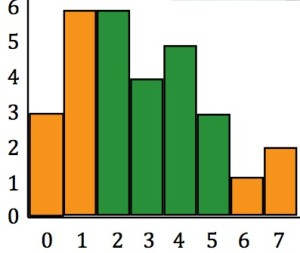
左边是原图,相当于前景,红色直方图就是引导向量。右边是背景图。想把左边红色部分移过去,但是又要变化最小,怎么办?那么就是计算
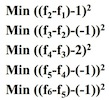 With f1 = 6, f6 = 1.
With f1 = 6, f6 = 1.
因为这些都是正数,也就相当于计算:
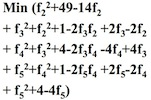
分开求偏导数
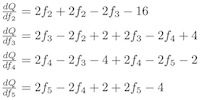
变化为矩阵
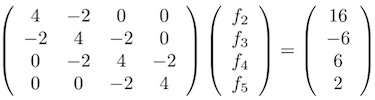
结论是:
f2 = 6, f3 = 4, f4 = 5, f5 = 3
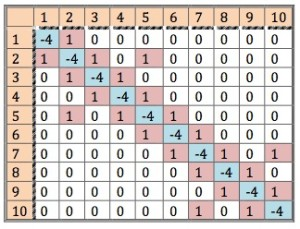
2-D EXAMPLE
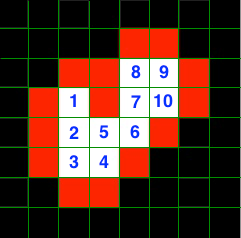
可以直接使用简化的方式,也就是拉普拉斯算子,进行卷积运算。
六、小结
现在看起来,Poisson Blending的却是很神奇的。固然它的理论还是比较复杂的,但是也只是在偏导数相关,并且最终可以简化为拉普拉斯。而我们更幸运,OpenCV中已经对其进行了不错的封装,我们可以直接调用!然而,对于原理的理解和思考,对于我们储备基础知识,解决更为复杂问题一定有帮助。
镇楼:

最后
以上就是贤惠鸡翅最近收集整理的关于Poisson Blending(Seamless clone)研究和实现的全部内容,更多相关Poisson内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复