【个人理解】计算for三层嵌套循环的时间复杂度

87 阅读 0 评论 58 点赞

我是靠谱客的博主土豪黑裤，最近开发中收集的这篇文章主要介绍【个人理解】计算for三层嵌套循环的时间复杂度，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

m=0

for(i=1;i<=N;i++)

    for(j=1;j<=i;j++)

        for(k=1;k<=j;k++)

            m++；

求时间复杂度

时间复杂度等于m的被执行的次数:

i=1时,m被执行一次：

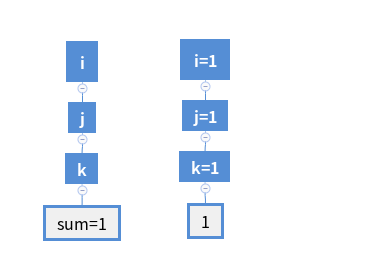
i=2时,m被执行1+3=4次：

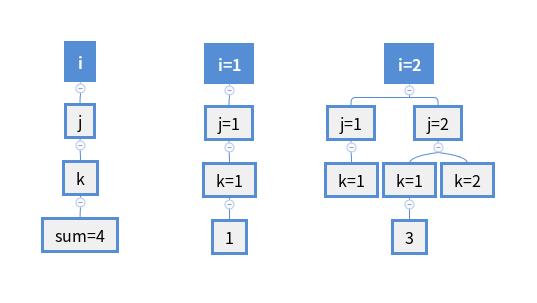
i=3时, m被执行1+3+6=10次：

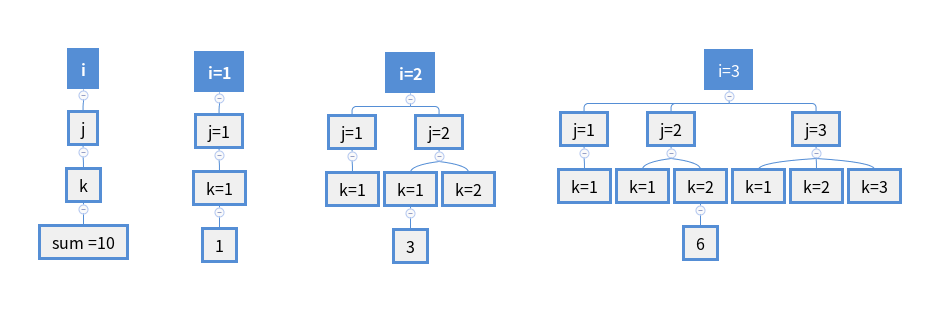
可以观察到，第i次循环次数是一个有规律的数列: 1, 3, 6, 10,... ...

设数列 $a_n$ ，其中 $a_1=1,;a_2=3,;a_3=6$ ,

那么观察可得，

$\a_1=1\a_2=3=1+2=a_1+2\a_3=6=1+2+3=a_2+3\...$ ,

则

$\a_n=a_{n-1}+n\=a_{n-2}+(n-1)+n\=a_{n-2}+(n-1)+n\=...\=a_1+2+3+...+(n-1)+n\=1+2+3+...+(n-1)+n\=frac{n(n+1)}{2}$ ;

也就得到了第i次循环的通项公式 $a_n=frac{n(n+1)}{2}$ .

i=n时,m++执行 $frac{n(n+1)}{2}$ 次：(图片中sum公式有误,具体请看下方推导)

知道了第n次循环m的执行次数,再全部加起来就能知道总的次数,也就是求数列 $a_n$ 的前n项和:

又因为 $a_{n-1}=frac{(n-1)(n-1+1)}{2}=frac{n^2}{2}-frac{n}{2}$ ;

所以数列an前n-1项和

$\S_{n-1}=frac{1}{2}(1^2+2^2+3^2+...+n^2)-frac{1}{2}(1+2+3+...+n) \=frac{1}{2}frac{n(n+1)(2n+1)}{6}-frac{(n+1)}{2} \=frac{n(n^2-1)}{6} \=frac{n^3-n}{6}$ .

把(n-1)换成n,也就是数列 $a_n$ 前n项和 $S_{n}=frac{(n+1)^3-(n+1)}{6}$ ;

即m++的执行次数也是 $S_{n}=frac{(n+1)^3-(n+1)}{6}$ .

代入数据,验证正确.

最后,可以看出n的最高次幂为 $n^3$ ,因此三重循环的时间复杂度是 $O(n^3)$ .

最后

以上就是土豪黑裤为你收集整理的【个人理解】计算for三层嵌套循环的时间复杂度的全部内容，希望文章能够帮你解决【个人理解】计算for三层嵌套循环的时间复杂度所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：数据结构
浏览次数：87 次浏览
发布日期：2023-07-02 04:05:03
本文链接：https://www.kaopuke.com/article/k-p-k_14_uzo_26_f4_14_z_6_w.html

【个人理解】计算for三层嵌套循环的时间复杂度

概述

最后

评论列表共有 0 条评论

发表评论取消回复

【个人理解】计算for三层嵌套循环的时间复杂度

概述

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

发表评论取消回复