星星之火-41：LTE 20M带宽时，为什么是2048个采样点？

1. 说明

这里“采样”与奈奎斯特采样定理中的“采样”完全是两码事，很容易混淆在一起。

奈奎斯特采样定理中的“采样”，是指用每隔一定时间的信号样值序列来代替原来在时间上连续的信号（时域信号），也就是在时间上将模拟信号离散化。这个的采样频率与时域信号中的最大的频率分量先关，是最大频率分量的2倍，以便能够通过时域的离散点恢复时间连续的信号。按照这个规则，20M的OFDM基带时域波形，需要至少40M的采样率，才能还原时域波形。

而这里的“采样”，是指快速傅里叶逆变换IFFT，需要一次性提供多少个输入“样本”值（频域信号），生成的时域波形是多少个采样点，这个采样频率与子载波的个数以及快速傅里叶逆变换IFFT的规则相关。20M的LTE带宽，经过快速傅里叶逆变换IFFT，生产的时域信号，只需要2048个采样点，采样率为15K * 2048 = 30.72M < 40M, 这是快速傅里叶变换带来的优势。

怎么做到的呢？这需要分析快速傅里叶逆变换IFFT和快速傅里叶变换FFT了。

2. LTE调制解调的架构

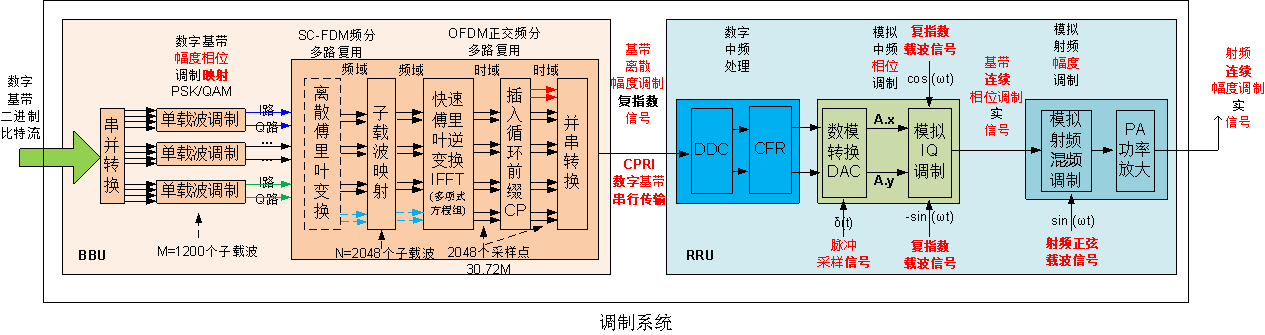
3. 快速傅里叶变换FFT

任何时域波形，都可以表达成 

令，则得到时域信号的多项式表达：

其中， 是n个未知数。

如果能够求出, 这n个未知数，就需要时域波形的n个点，{（x0,y0），（（x1,y1），（x2,y2）.....(xn,yn) }

有这n个点的对应关系，就能够求出多项式的参数。

而这n个点.(xi,yi），就是一个符号周期内的时域的采样点，其中xi离散的采样时间，yi为某一时间对应的采样幅度值。

......

当m=n-1，就是n个采样点，通过计算方程组，就可以得到N次多项式的N个系数。

上述过程，就是快速傅里叶变换的过程。

很显然，快速傅里叶变换，能够通过N采样点，就可能够轻松的、快速的、获取通过N次多项式表达时域波形的N个多项式的系数。

上述过程，也是OFDM的接复用过程！

这里会得到一个神奇的结果：

20M的LTE带宽的时域波形，只需要2048个采样点，采样率为15K * 2048 = 30.72M < 40M, 就可以还原出时域信号中每个频率分量，这是快速傅里叶变换带来的优势。

快速傅里叶变换有一个前提调节：组成时域波形的N个谐波频率，能够组成N次多相似的关系，即能够用N次多项式表达时域波形。

看到这里，还还看到一个奇怪的现象，就是20M的LTE带宽，有效子载波只有1200个，为什么这里有2048个参数，即2048个子载波？

这是快速傅里叶变换FFT本身的要求，它要求多项式的次数必须是， 1200个子载波，扩展成了2048.

多出来的子载波怎么办？如何处理它们？

• 快速傅里叶逆变换FFT调制复用时，为这些多余的子载波，指定它们的系数恒为0值。
• 快速傅里叶变换FFT解调解复用时，计算出来的这些多余的系数全部忽略。

4. 快速傅里叶逆变换IFFT

快速傅里叶逆变换IFFT的过程，就是按照快速傅里叶变换FFT的要求，构建一个N次多项式表达时域波形，并且同N个采样点代表该时域波形。如下图所示。

......

当An-1, An-2......A1，A0已知时：

就是一个确定性的函数，其中

假设采样周期为Ts，则t=Ts, 2Ts, 3Ts......(n-1)Ts时，就可以得到函数y(x)的采样点(Xn-1, Yn-1）， (Xn-2,Yn-2），......(X1，Y1), (X0, Y0).

每个采样点的值，完全由An-1, An-2......A1，A0确定。

在快速傅里叶逆变换IFFT实现OFDM调制时，An-1, An-2......A1，A0实际上，就是各个子载波的幅度值，由各个子载波的QAM调制映射值决定。

5. OFDM调制信号的时域采样率

15K带宽时，1个子载波符号，就是1个FFT输入采样点。此是的时域的采样率1 * 15K = 15K, 时域的采样周期为1/15K=66.67us，表示一秒钟有15K个子载波的幅度值。

10M带宽时，  600个子载波符号，就是1024个FFT输入采样点。此是的时域的采样率=1024 * 15K = 15.36M，表示一秒钟有15.36M个子载波的幅度值。

20M带宽时，1200个子载波符号，就是2048个FFT输入采样点。此是的时域的采样率=1024 * 15K = 30.72M，表示一秒钟有30.72M个子载波的幅度值。

如下图所示：

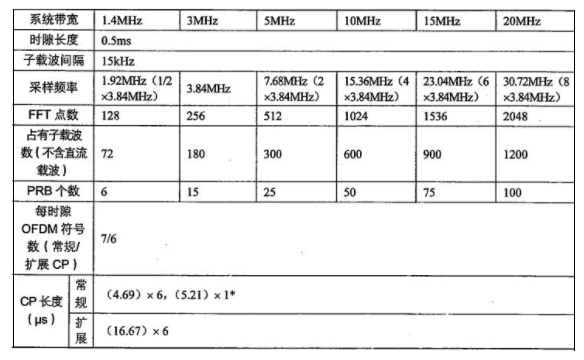
最后

以上就是清秀雨为你收集整理的星星之火-41：LTE 20M带宽时，为什么是2048个采样点？的全部内容，希望文章能够帮你解决星星之火-41：LTE 20M带宽时，为什么是2048个采样点？所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。