现代通信原理10.2：采用匹配滤波器的数字基带传输系统误码性能分析

  在上一节里面，我们讨论了接收滤波器采用低通滤波器，这其实是延续了模拟系统的做法，通过低通滤波器限制进入接收机的噪声功率。但在数字系统里，这并不是最好的做法。所以这一节，我们讨论最佳接收机，也就是匹配滤波器。所以，我们先来看看，什么是匹配滤波器；再用匹配滤波器作为接收滤波器，分析系统的误码性能。

1、匹配滤波器

  在图1中，滤波器$h(t)$的输入信号$x(t)=s(t)+n_w(t)$，其中$s(t)$为有用信号，$n_w(t)$为单边功率谱密度为$N_0$的加性高斯白噪声；滤波器输出信号为$y(t)=x(t)\ast h(t)=s_o(t)+n(t)$，这里$s_o(t)=s(t)\ast h(t)$，$n(t)=n_w(t)\ast h(t)$。

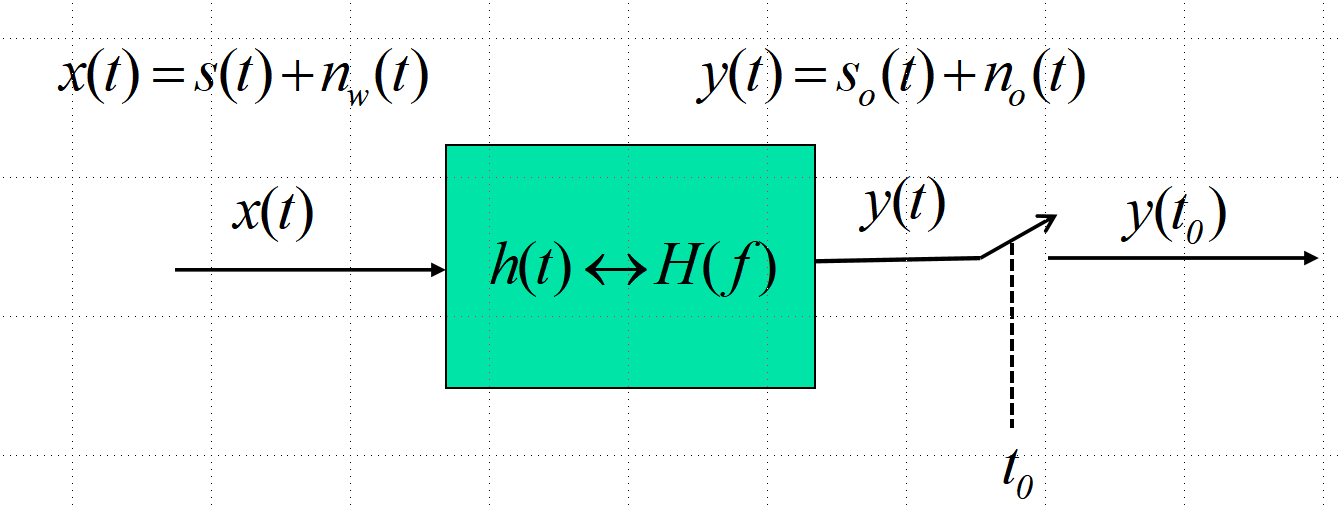
1.1 匹配滤波器定义

  对于输出信号$y(t)$，我们定义在$t_0$时刻的输出信噪比为有用信号$s_o(t)$的瞬时功率$s_o^2(t_0)$与输出噪声$n(t)$的平均功率之比，即
$${\eta }_0=\frac{s_o^2(t_0)}{E[n^2(t)]}\text{\hspace{1em}(1)}$$在时刻$t_0$，能够使输出信噪比${\eta }_0$最大的线性滤波器，被称为信号$s(t)$的匹配滤波器。

1.2 匹配滤波器的冲激响应

  下面我们来推导匹配滤波器的冲激响应$h(t)$与频域传递函数$H(f)$。由于
$$s_o(t)=s(t)\ast h(t)\leftarrow \to S_o(f)=S(f)H(f),$$有
$$s_o(t)={\int }_{-\infty }^{\infty }{S}_o(f)e^{j2\pi f_t}df={\int }_{-\infty }^{\infty }S(f)H(f)e^{j2\pi ft}df$$因此，可以得到信号$s_o(t)$在$t_0$时刻的取值为
$$s_o(t_0)={\int }_{-\infty }^{\infty }S(f)H(f)e^{j2\pi f{t}_0}df,$$其瞬时功率为
$$s_o^2(t_0)=|{\int }_{-\infty }^{\infty }S(f)H(f)e^{j2\pi f{t}_0}df{|}^2.$$对于输出噪声$n_o(t)$，由于$n(t)$的功率谱密度为
$$P_{N_w}(f)=\frac{N_0}{2},-\infty <f<\infty$$因此，滤波器$H(f)$输出噪声$n(t)$的功率谱密度为
$$P_N(f)=\frac{N_0}{2}|H(f){|}^2,$$平均功率为$P_N={\int }_{-\infty }^{\infty }{P}_N(f)df$。输出信噪比可以进一步写成
$${\eta }_0=\frac{|{\int }_{-\infty }^{\infty }S(f)H(f)e^{j2\pi f{t}_0}df{|}^2}{{\int }_{-\infty }^{\infty }\frac{N_0}{2}|H(f){|}^{2}df}$$

施瓦尔兹不等式：
$$|{\int }_{-\infty }^{\infty }X(f)H(f)df{|}^2\le {\int }_{-\infty }^{\infty }|X(f){|}^{2}df{\int }_{-\infty }^{\infty }|H(f){|}^{2}df$$当且仅当$X(f)=K{H}^{\ast }(f)$时，等号成立。

  根据施瓦尔兹不等式，有
$$\begin{array}{rl}{\eta }_0& =\frac{|{\int }_{-\infty }^{\infty }H(f)[S(f)e^{j2\pi f{t}_0}]df{|}^2}{\frac{N_0}{2}{\int }_{-\infty }^{\infty }|H(f){|}^{2}df}\\ & =\frac{{\int }_{-\infty }^{\infty }|H(f){|}^{2}df\cdot {\int }_{-\infty }^{\infty }|S(f){|}^{2}df}{\frac{N_0}{2}{\int }_{-\infty }^{\infty }|H(f){|}^{2}df}\\ & =\frac{{\int }_{-\infty }^{\infty }|S(f){|}^{2}df}{\frac{N_0}{2}}\\ & =\frac{2E_s}{N_0}\end{array}\text{\hspace{1em}(2)}$$其中，$E_s={\int }_{-\infty }^{\infty }|S(f){|}^{2}df={\int }_{-\infty }^{\infty }{s}^2(t)|dt$为信号$s(t)$的能量。显然，(2)中等号成立的条件为
$$H(f)=K{S}^{\ast }(f)e^{-j2\pi f{t}_0},\text{\hspace{1em}(3)}$$此时，可以得到信噪比最大值为
$${\eta }_{0,\max }=\frac{2E_s}{N_0}.\text{\hspace{1em}(4)}$$进一步，可以得到匹配滤波器的冲激响应为
$$\begin{array}{rl}h(t)& ={\int }_{-\infty }^{\infty }H(f)e^{-j2\pi ft}df={\int }_{-\infty }^{\infty }K{S}^{\ast }(f)e^{-j2\pi f{t}_0}{e}^{-j2\pi ft}df\\ & =K{\int }_{-\infty }^{\infty }[{\int }_{-\infty }^{\infty }s(\tau )e^{-j2\pi f\tau }d\tau {]}^{\ast }{e}^{-j2\pi f(t_0-t)}df\\ & =K{\int }_{-\infty }^{\infty }[{\int }_{-\infty }^{\infty }{e}^{j2\pi f(\tau -t_0+t)}df]s(\tau )d\tau \\ & =K{\int }_{-\infty }^{\infty }\delta (\tau -t_0+t)s(\tau )d\tau \\ & =Ks(t_0-t).\end{array}\text{\hspace{1em}(5)}$$

1.3 匹配滤波器的物理可实现性

  根据(5)可知，在图1中，为了使得滤波器$h(t)$的输出信噪比在$t_0$达到最大值，有$h(t)=Ks(t_0-t)$，此时信噪比最大值为${\eta }_{0,\max }=\frac{2E_s}{N_0}$。进一步，考虑滤波器的物理可实现性，有当$t<0$时，$h(t)=0$。设$t^{\prime }=t_0-t$，有$h(t_0-t^{\prime })=Ks(t^{\prime })$，因此得到当$t^{\prime }>t_0$时，$s(t^{\prime })=0$。也就是说，为了保证与$s(t)$匹配的滤波器$h(t)$的物理可实现性，信号$s(t)$应该在信噪比达到最大值的时刻点$t_0$之前结束。

1.4 用相关器来等效匹配滤波器

  在图1中，若滤波器的输入信号为$x(t)=s(t)+n_w(t)$，为了使得输出信号$y(t)=s_o(t)+n(t)$在$t_0$时刻的信噪比达到最大，我们采用匹配滤波器$h(t)=s(t_0-t)$，因此可以得到输出信号为
$$\begin{array}{rl}y(t)& =x(t)\ast h(t)={\int }_0^{t}x(\tau )h(t-\tau )d\tau \\ & ={\int }_0^{t}x(\tau )s(t_0-t+\tau )d\tau \\ & ={\int }_0^t[s(\tau )+n_w(\tau )]s(t_0-t+\tau )d\tau \end{array}\text{\hspace{1em}(6)}$$根据物理可实现条件，我们取$t_0=T$，这里$T$为信号$s(t)$结束的时刻，因此有
$$\begin{array}{r}y(t)={\int }_0^t[s(\tau )+n_w(\tau )]s(T-t+\tau )d\tau \end{array}\text{\hspace{1em}(6)}$$进一步，$t=T$时刻$y(t)$抽样值为
$$y(T)={\int }_0^T[s(\tau )+n_w(\tau )]s(\tau )d\tau \text{\hspace{1em}(7)}$$从(7)可以看出，我们可以用图2所示的相关器来等效匹配滤波器，这样在$t=T$点的抽样值是相同的。由于相关器不需要滤波器的卷积运算，在分析时候更简单，因此在后面的讨论中，我们大多采用相关器进行分析。在图2中可以看到，由于滤波器是与$s(t)$匹配，因此相关器中是与$s(t)$相乘，并且在时刻$T$抽样。

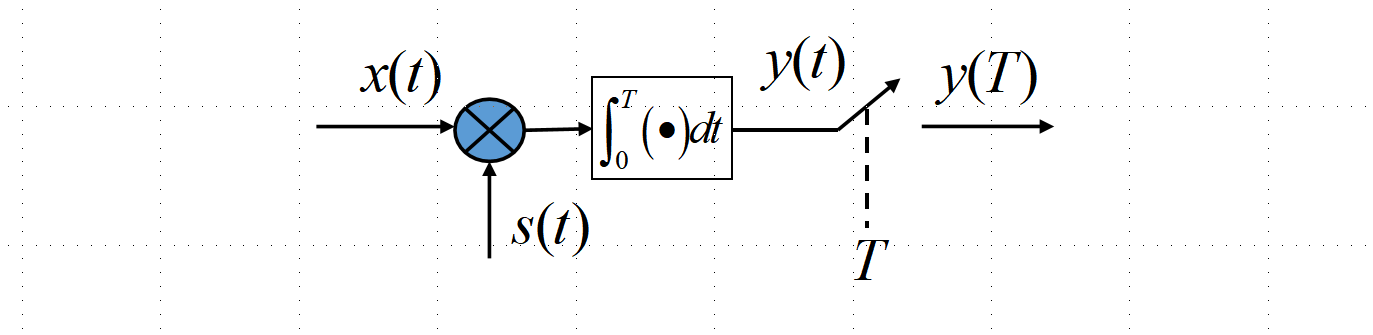
2、采用匹配滤波器的二进制基带传输系统误码性能分析

2.1 系统模型

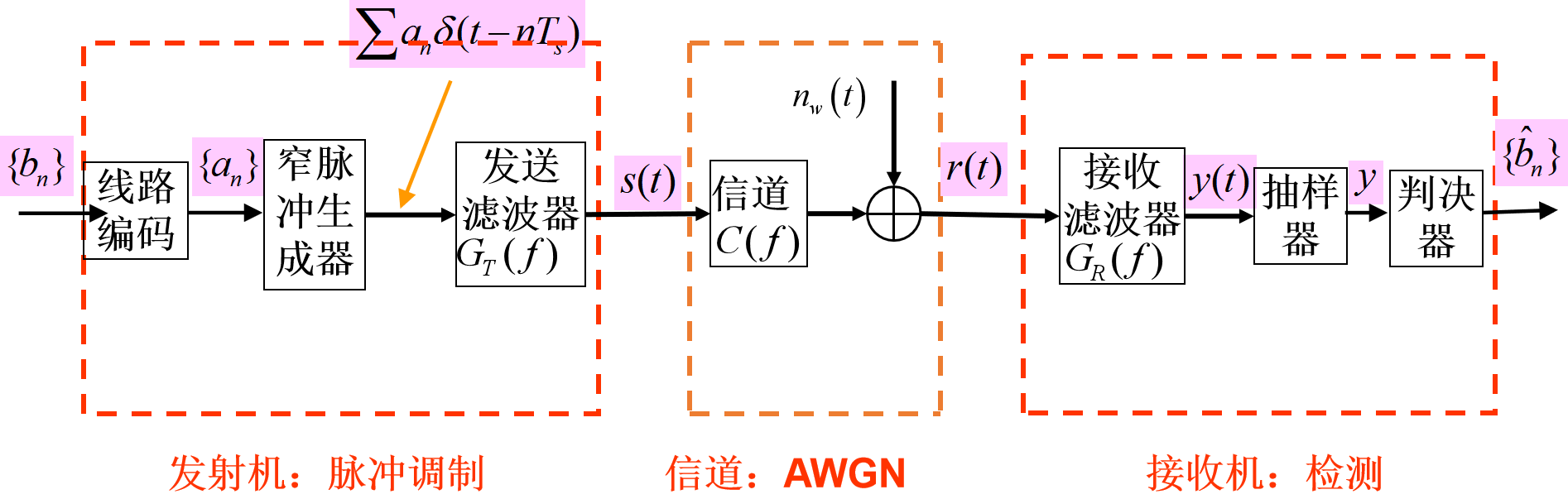
  从图3看出，在发射机中，我们首先进行线路编码，随后通过窄脉冲和脉冲成型，产生发送信号$s(t)$。这里我们考虑二进制系统，即发射机发送两种不同信号波形，分别表示"1"和"0"。例如，我们可以用图4(a)中的$s_1(t)$和(b)中$s_2(t)$，分别表示“1”和“0”。

  发射机发送的信号$s_i(t),i=1,2$，经过信道后到达接收机，因此接收信号可以表示为：
$$r(t)=s(t)\ast c(t)+n_w(t),\text{\hspace{1em}(8)}$$这里$c(t)$为信道的冲激响应，$n_w(t)$为加性高斯白噪声。
  这里我们考虑带宽无限的理想AWGN信道，因此有到达接收机的信号为
$$r(t)=s(t)+n_w(t).\text{\hspace{1em}(9)}$$

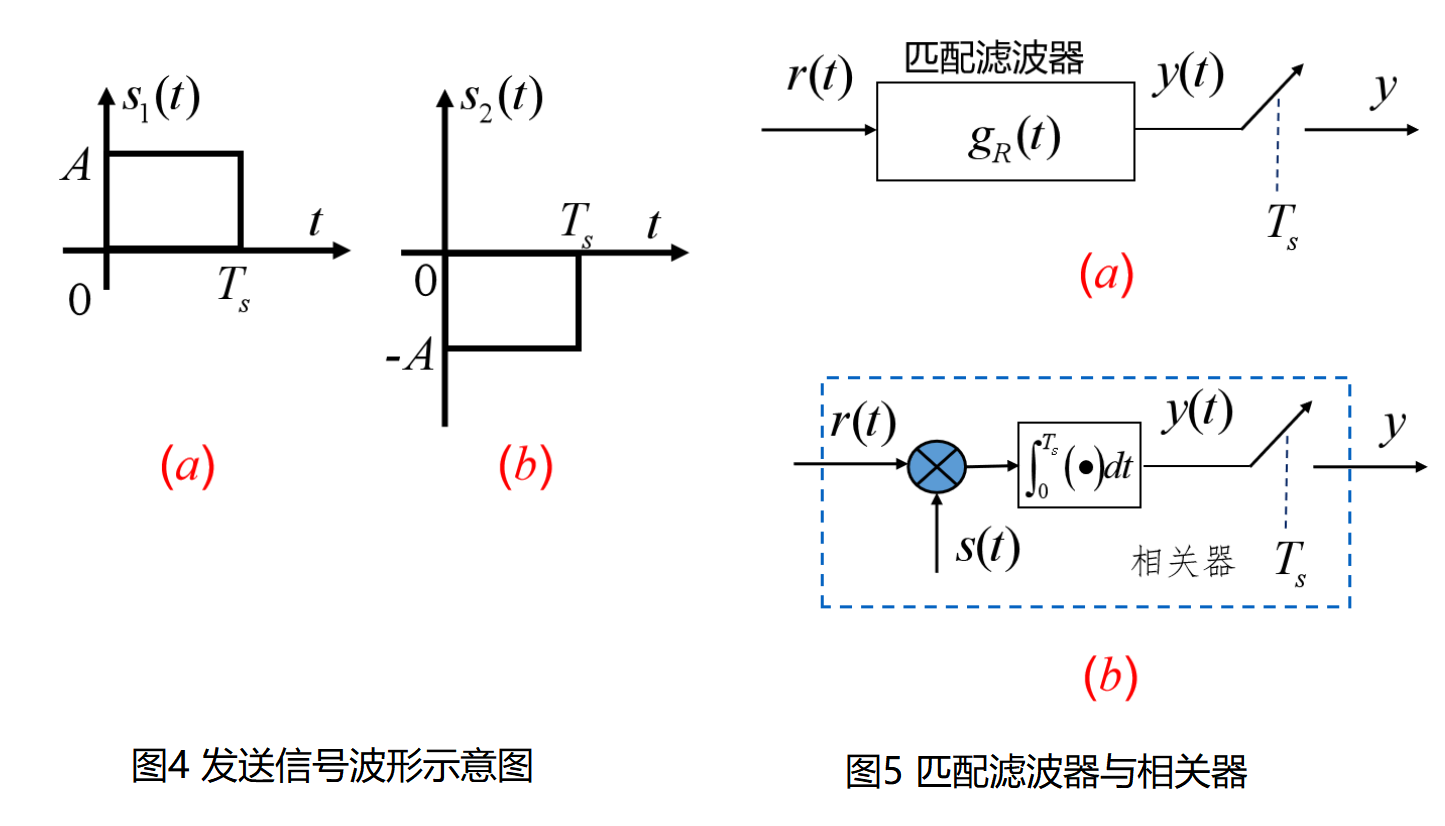
  下面我们来讨论接收滤波器$g_R(t)$的设计。采用与$s_1(t)$相匹配的MF，我们可知$g_R(t)=s_1(T_s-t)$，这里的$T_s$为信号$s_1(t)$持续时间，如图4所示。

2.2 判决变量$y$的条件概率密度函数

  图3中，接收滤波器$g_R(t)$输出的信号$y(t)$，在$T_s$点进行抽样后，得到判决变量$y$，再对$y$进行判决。在图5中，我们用相关器来等效匹配滤波器。

（1）发送信号为$s_1(t)$时的判决变量

  若发射信号为$s_1(t)$，接收信号$r(t)=s_1(t)+n_w(t)$，可以得到判决变量为
$$\begin{array}{rl}y& =y(T_s)={\int }_0^{T_s}[s_1(\tau )+n_w(\tau )]s_1(\tau )d\tau \\ & ={\int }_0^{T_s}{s}_1^2(\tau )d\tau +{\int }_0^{T_s}{s}_1(\tau )n_w(\tau )d\tau \\ & =E_{s1}+Z.\end{array}\text{\hspace{1em}(10)}$$其中$E_{s1}={\int }_0^{T_s}{s}_1^2(\tau )d\tau$为信号$s_1(t)$的能量，噪声项
$$\begin{array}{r}Z={\int }_0^{T_s}{s}_1(\tau )n_w(\tau )d\tau \end{array}\text{\hspace{1em}(11)}$$的条件均值为
$$\mathrm{E}(Z|s_1)=0\text{\hspace{1em}(12)}$$方差为
v a r ( Z ∣ s 1 ) = E { [ Z − E ( Z ) ] 2 ∣ s 1 } = E [ ∫ 0 T s ∫ 0 T s n w ( t 1 ) n w ( t 2 ) s 1 ( t 1 ) s 1 ( t 2 ) d t 1 d t 2 ] = ∫ 0 T s ∫ 0 T s E [ n w ( t 1 ) n w ( t 2 ) ] s 1 ( t 1 ) s 1 ( t 2 ) d t 1 d t 2 . (13) tag{13} begin{aligned} {rm var}(Z|s_1)&={rm E}{Large {}[Z-{rm E}(Z)]^2|s_1{Large }}\ &={rm E}{Large [}int_0^{T_s}int_0^{T_s}n_w(t_1)n_w(t_2)s_1(t_1)s_1(t_2)dt_1dt_2 {Large ]}\ &=int_0^{T_s}int_0^{T_s}{rm E}{Large [}n_w(t_1)n_w(t_2){Large ]}s_1(t_1)s_1(t_2)dt_1dt_2. end{aligned} var(Z∣s1​)​=E{[Z−E(Z)]2∣s1​}=E[∫0Ts​​∫0Ts​​nw​(t1​)nw​(t2​)s1​(t1​)s1​(t2​)dt1​dt2​]=∫0Ts​​∫0Ts​​E[nw​(t1​)nw​(t2​)]s1​(t1​)s1​(t2​)dt1​dt2​.​(13)其中，
$$\mathrm{E}[n_w(t_1)n_w(t_2)]=R_w(\tau )=\frac{N_0}{2}\delta (\tau ),\tau =t_2-t_1,\text{\hspace{1em}(14)}$$这里$R_w(\tau )$为AWGN的自相关函数。将(14)代入(13)，可以得到
$$\begin{array}{rl}\mathrm{v}\mathrm{a}\mathrm{r}(Z|s_1)& =\frac{N_0}{2}{\int }_0^{T_s}{s}_1^2(t)dt=\frac{N_0}{2}{E}_{s1}.\end{array}\text{\hspace{1em}(15)}$$显然，我们有$Z\sim \mathcal{N}(0,\frac{N_0}{2}{E}_{s1})$，故$y\sim \mathcal{N}(E_s,\frac{N_0}{2}{E}_{s1})$。
  因此，我们可以得到发送信号为$s_1(t)$时判决变量$y$的条件概率密度函数为
$$p(y|s_1)=\frac{1}{\sqrt{2\pi }{\sigma }_n}{e}^{-\frac{(y-E_{s1}{)}^2}{2{\sigma }_n^2}},\text{\hspace{1em}(16)}$$其中${\sigma }_n^2=\frac{N_0}{2}{E}_{s1}$为(15)推导得到的噪声平均功率。

（2）发送信号为$s_2(t)$时的判决变量

  若发射信号为$s_2(t)$，我们按照上面步骤进行推导，可以得到判决变量为
$$y={\int }_0^{T_s}{s}_1(\tau )s_2(\tau )d\tau +Z\text{\hspace{1em}(17)}$$因此$y\sim \mathcal{N}(R_{12},\frac{N_0}{2}{E}_s)$，这里${\rho }_{12}={\int }_0^{T_s}{s}_1(t)s_2(t)dt$为信号$s_1(t)$与$s_2(t)$的相关系数。我们分别考虑单极性和双极性两种情况。若为单极性波形，即$s_2(t)=0$，有${\rho }_{12}=0$，因此可以得到发送信号为$s_2(t)$时判决变量$y$的条件概率密度函数为
$$p_{(}y|s_2)=\frac{1}{\sqrt{2\pi }{\sigma }_n}{e}^{-\frac{y^2}{2{\sigma }_n^2}}.\text{\hspace{1em}(18)}$$若为双极性波形，即$s_2(t)=-s_1(t)$，有${\rho }_{12}=-{\int }_0^{T_s}{s}_1^2(t)dt=-E_{s1}$，因此可以得到发送信号为$s_2(t)$时判决变量$y$的条件概率密度函数为
$$p(y|s_2)=\frac{1}{\sqrt{2\pi }{\sigma }_n}{e}^{-\frac{(y+E_{s1}{)}^2}{2{\sigma }_n^2}}.\text{\hspace{1em}(19)}$$

2.3 码元错误概率公式推导

  单极性以及双极性情况下，判决变量$y$的条件概率密度函数曲线分别如图6中(a)和(b)所示。我们假定$s_1(t)$和$s_2(t)$分别代表二进制信息的"1"和“0”，且二者发送概率相等，即$P_0=P_1=\frac{1}{2}$，因此系统的误码率为$P_e=\frac{1}{2}(P_{e0}+P_{e1})$，其中
$$P_{e0}=\mathrm{P}\mathrm{r}(y>V_T|s_2)$$为发送’0’时候的错误概率，$V_T$为判决门限；而
$$P_{e1}=\mathrm{P}\mathrm{r}(y<V_T|s_1)$$为发送’0’时候的错误概率。由于“0”、“1”发送概率相等，因此最佳判决门限取在两条条件概率曲线均值的重点，即单极性时$V_T=\frac{E_s}{2}$，双极性时$V_T=0$。

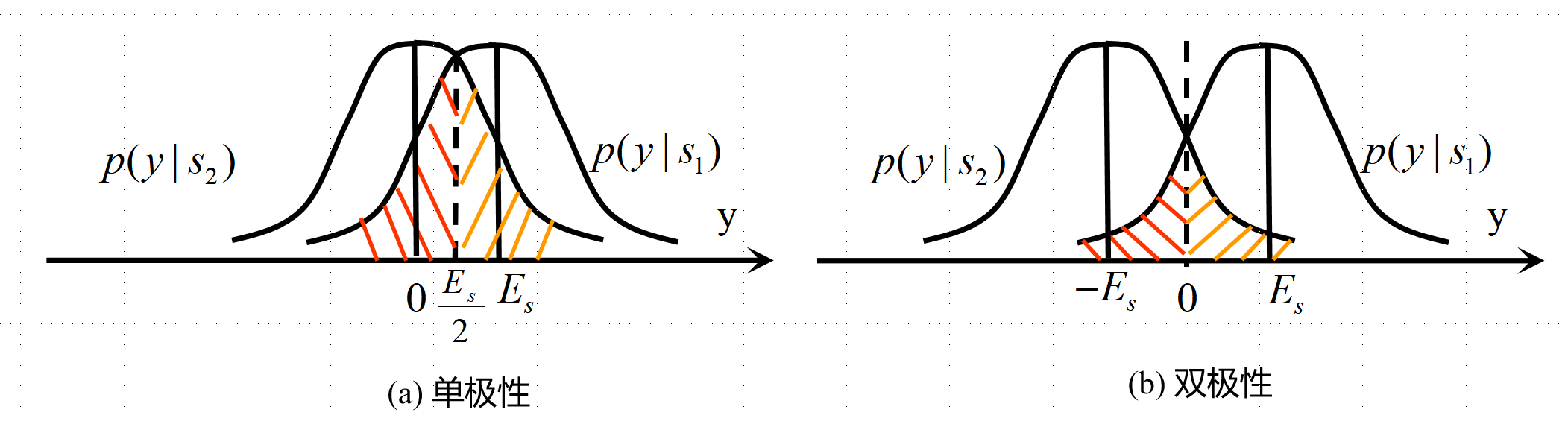
  与上一节低通滤波器的推导类似，我们可以得到发$s_1(t)$时的误码率为红色阴影部分，即单极性时为
$$P_{e,单}=Q(\frac{E_{s1}/2}{{\sigma }_n}),$$双极性时候为$$P_{e,双}=Q(\frac{E_s}{{\sigma }_n}),$$将${\sigma }_n^2=\frac{N_0}{2}{E}_{s1}$代入，有
$$P_{e,单}=Q(\sqrt{\frac{E_{s1}}{2N_0}}),\text{\hspace{1em}(20)}$$以及$$P_{e,双}=Q(\sqrt{\frac{2E_{s1}}{N_0}}).\text{\hspace{1em}(21)}$$进一步，我们注意到对于双极性信号，有$s_1(t)$与$s_2(t)$的信号能量相等，即$E_{s1}=E_{s2}$，因此信号的平均功率为$E_s=E_{s1}=E_{s2}$；对于单极性信号，$s_1(t)$的信号能量为$E_{s1}$，而$s_2(t)$的信号能量为0，如果$s_1(t)$与$s_2(t)$出现概率相等，则信号$s(t)$的平均功率为$E_s=\frac{E_{s1}+E_{s2}}{2}=\frac{E_{s1}}{2}$。将$E_s$代入(20)和(21)中，有
$$P_{e,单}=Q(\sqrt{\frac{E_s}{N_0}}),\text{\hspace{1em}(22)}$$以及$$P_{e,双}=Q(\sqrt{\frac{2E_s}{N_0}}).\text{\hspace{1em}(23)}$$

最后

以上就是优雅西装为你收集整理的现代通信原理10.2：采用匹配滤波器的数字基带传输系统误码性能分析的全部内容，希望文章能够帮你解决现代通信原理10.2：采用匹配滤波器的数字基带传输系统误码性能分析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。