概述
文章目录
- 问题提出
- 数据
- 问题的求解
- 数据预处理
- 编写程序求解
问题提出
考查鸢尾属植物中两个不同品种的花的如下四个形状指标： X 1 X_1 X1 位萼片长度； X 2 X_2 X2 位萼片宽度； X 3 X_3 X3 为花瓣长度； X 4 X_4 X4 为花瓣宽度。现验证：该形状指标数据（两个品种）总体是否服从四维正态分布？
数据
数据采用 鸢尾属植物两个不同品种的花的形状数据1，其中部分数据如下：
| 编号 | 品种 | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 |
|---|---|---|---|---|---|
| 1 | 1 | 65 | 28 | 46 | 15 |
| 2 | 1 | 62 | 22 | 45 | 15 |
| … | … | … | … | … | … |
| 50 | 1 | 67 | 30 | 50 | 17 |
| 51 | 2 | 64 | 28 | 56 | 22 |
| 52 | 2 | 67 | 31 | 56 | 24 |
| … | … | … | … | … | … |
| 100 | 2 | 63 | 33 | 60 | 25 |
问题的求解
数据预处理
将上述数据的四项形状指标数据保存于 datas.txt 文档中。
编写程序求解
MATLAB 代码如下：
X = load('datas.txt'); % 导入数据
[N, p] = size(X);
d = mahal(X, X); % 计算马氏距离
d1 = sort(d); % 从小到大排序
pt = [[1:N] - 0.5] / N; % 计算分位数
x2 = chi2inv(pt, p); % 计算 X^2_t
plot(d1, x2, '*', [0:13], [0:13], '-r') % 作图
绘制图像如下：
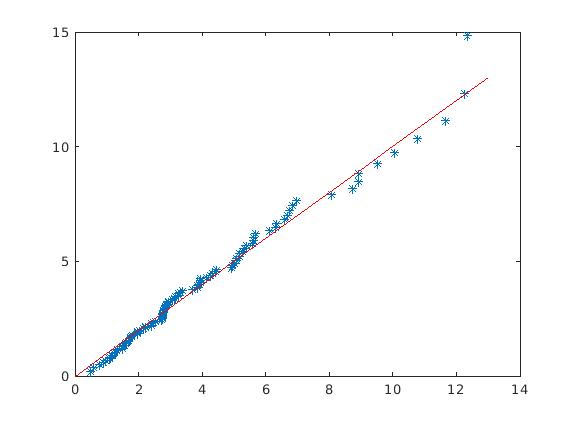
从图像可以看出，数据点基本落在直线上，故不能拒绝该数据服从四维正态分布的假设。
数据来源：梅长林，范金城，数据分析方法，高等教育出版社。 ↩︎
最后
以上就是害羞墨镜为你收集整理的MATLAB利用QQ图检验总体是否服从多维正态分布问题提出数据问题的求解的全部内容，希望文章能够帮你解决MATLAB利用QQ图检验总体是否服从多维正态分布问题提出数据问题的求解所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复