数字图像处理—图像分割

概述：

1. 在对图像的研究和应用中，人们往往仅对图像中的某些部分感兴趣，这些部分一般称为目标或前景。
2. 为了辨识和分析目标，需要将有关区域分离提取出来，在此基础上对目标进一步利用，如进行特征提取和测量。
3. 图像分割就是指把图像分成各具特性的区域并提取出感兴趣目标的技术和过程。
4. 特性可以是灰度、颜色、纹理等，目标可以对应单个区域，也可以对应多个区域。
5. 图像分割是图像识别和图像理解的基本前提步骤。

图像分割算法：基于亮度值的不连续性和相似性。

1. 不连续性是基于亮度的不连续变化分割图像，如图像的边缘。
2. 根据制定的准则将图像分割为相似的区域，如阈值处理、区域生长、区域分离和聚合。

（一）点、线和边缘检测

1.1 点检测

使用如下图所示的模板，如果:

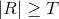
则在模板中心位置检测到一个点。其中，T是阈值，R是模板计算值。

基本思想：如果一个孤立点与它周围的点不 同，则可以使用上述模板进行检测。

注意：如果模板响应为0，则表示在灰度级为常数的区域。

函数：

g = abs(imfilter(tofloat(f), w)) >= T;

其中，f 是输入图像，w 是适合点检测的模板，g 是包含检测点的图像。

f = imread('D:数字图像处理第十章学习Fig1002(a).tif');
w = [-1 -1 -1;-1 8 -1;-1 -1 -1];                    % 点检测掩模
g = abs(imfilter(double(f),w));
T = max(g(:));
g = g>=T;
subplot(1,2,1);imshow(f);title('(a)原图像');
subplot(1,2,2);imshow(g);title('(b)点检测');

分析：

图 (a)显示了一幅图像f，在球体的东北象限有一个几乎不可见的黑点，检测该点，在滤波后的图像g中选择最大值作为 T值。然后在g中寻找所有的g>=T的点。假设所有的点是孤立的镶嵌在恒定或是近似恒定的背景上。我们可识别能给出最大响应的点。因为在选择g中的最大值作为T值的情况下，在g中不存在比T值大的点。我们使用>=算子(代替＝)定 义一致性。如图 (b)所示，其中有一个孤立点，该点使用 T值置为max(g (: ))且满足g>=T 的条件。

1.2 线检测

通过比较典型模板的计算值，确定一个点是否在某个方向的线上。

也可以设计其他模板：

1. 模板系数之和为0。
2. 感兴趣的方向系数值较大。

该模板对水平线有最大响应（水平模板）

该模板对45°方向线有最大响应（45°模板）

该模板对垂直线有最大响应（垂直模板）

该模板对-45°方向线有最大响应（135°模板）

用R1,R2,R3和R4分别代表水平、45°、垂直和 -45°方向线的模板响应，在图像中心的点，如果
|Ri|>|Rj|，j不等于i，则此点被认为与在模板i方向上的线更相关。

例：如果|$R_i$|>|$R_j$|，j=2,3,4，
则该点与水平线有更大的关联。
在灰度恒定的区域，上述4个模板的响应为零。

检测指定方向的线 :

f = imread('D:数字图像处理第十章学习Fig1004(a).tif');     % 图像大小：486×486
w = [2 -1 -1;-1 2 -1;-1 -1 2];          % +45°方向检测线
g = imfilter(double(f),w);
gtop = g(1:120,1:120);                  % 左上角区域
gtop = pixeldup(gtop,4);                % 通过复制像素将图像扩大gtop*4倍
gbot = g(end-119:end,end-119:end);      % 右下角区域
gbot = pixeldup(gbot,4);
g1 = abs(g);                             % 检测图的绝对值
T = max(g1(:));
g2 = g1>=T;

subplot(3,2,1);imshow(f);title('(a)连线模板图像');
subplot(3,2,2);imshow(g,[]);title('(b)+45°线处理后的结果');
subplot(3,2,3);imshow(gtop,[]);title('(c)(b)中左上角的放大效果');
subplot(3,2,4);imshow(gbot,[]);title('(d)(b)中右下角的放大效果');
subplot(3,2,5);imshow(g1,[]);title('(e)(b)的绝对值');
subplot(3,2,6);imshow(g2);title('(f)满足g>=T的所有点');

分析：

1. 图 (a)显示了一幅数字化(二值化)的电子线路连线模板的一部分。图像大小是486×486 像素。
2. 在图 (b)中，比灰色背景暗一点的阴影与负值 相对应。在+45°方向上有两个主要线段，一个在左 上方，另一个在右下方(图©和图(d)显示了这 两个区域的放大的片段)。
3. 注意，在图 (d)中，直线部分比图 ©中的线段要亮得多。原因是：图 (a)中右下方的部分只有一个像素宽，但左上方的部分不是。模板的响应对一个像素宽的部分比较强烈。
4. 图(e)显示了图(b)的绝对值。因为我们对最强的响应感兴趣，所以令 T等于图像中的最大值。图 (f)以白色显示了满足条件g>=T的点，其中的 g是图(e)中的图像。

1.3 使用函数edge的边缘检测

边缘：

1. 边缘是指图像中像元灰度有阶跃变化或屋顶状变化的那些像元的集合。
2. 存在于目标与背景、目标与目标、区域与区域、基元与基元之间。
3. 包含方向、阶跃性质、形状等信息。
4. 是图像识别中抽取的重要属性，对图像识别和分析十分有用。

边缘的分类：

1. 阶跃状：位于两边的像素灰度值有明显不同。
2. 屋顶状：位于灰度值从增加到减少的转折处。

阶跃状边缘：

1. 一阶导数为极值点
2. 二阶导数为过零点

屋顶状边缘：

1. 一阶导数为过零点
2. 二阶导数为过极值点

边缘和导数（微分）的关系：

图解：边缘的一阶导数在图像由暗变亮的突变位置有一个正的峰值，而在图像由亮变暗的位置有一负的峰值，而在其他位置都为0。
分析：可用一阶导数的幅度值来检测边缘的存在，幅度峰值对应的一般就是边缘的位置，峰值的正或负就表示边缘处由暗变亮还是由亮变暗。同理，可用二阶导数的过0点检测图像中边缘的存在。二阶导数判断边缘像素在边缘亮的一边，还是暗的一边。

（a）梯度算子：

1. 对于阶跃边缘，在边缘点处一阶导数有极值，因此可计算每个像元处的梯度来检测边缘点。
2. 梯度的大小代表边缘的强度，梯度方向与边缘走向垂直。

函数f(x,y)在(x,y)处的梯度为一个向量：

梯度向量指向f变化率最大方向。

大小：

a(x,y)代表梯度向量在(x,y)处方向角。

边缘在(x,y)处方向与此点梯度向量方向垂直。

模板表示：
   
基于梯度的边缘检测：

选取适当的阈值T，对梯度图像进行二值化

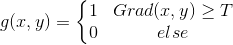
缺点：梯度算子仅用最近邻像素的灰度计算，对噪声敏感，无法抑制噪声的影响。

（b）Roberts交叉梯度算子 ：

语法：

[g, t] = edge(f, ‘roberts’,T, dir)

两个模板称为Roberts 交叉梯度算子
   
梯度计算由两个模板组成，第一个求得梯度的第一项，第二个求得梯度的第二项，然后求和，得到梯度。


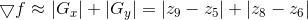
对应差分方程：


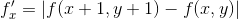
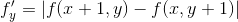
分析：这种算子进行边缘检测的同时去噪作用仍然小，但效果较梯度算子好。

（c）Prewitt梯度算子

3x3的梯度模板：
   

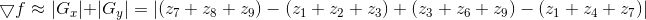
分析：不仅能检测边缘点，且能抑制噪声的影响。

（d）Sobel算子：

3x3的梯度模板
   

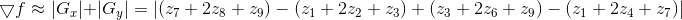
分析：

1. Prewitt和Sobel算子是计算数字梯度时最常用的算子。
2. Prewitt模板比Sobel模板简单，但Sobel模板能够有效抑制噪声。
3. 对4领域采用带权方法计算差分，能进一步抑制噪声，但检测的边缘较宽。

（e）拉普拉斯算子：

定义：二维函数f(x,y)的拉普拉斯是一个二阶的微分定义为：

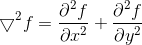
模板：定义数字形式的拉普拉斯的基本要求是，作用于中心像素的系数是一个负数，而且其周围像素的系数是正数，系数之和必为0。对于一个3x3的区域，经验上被推荐最多的形式是：

离散形式：

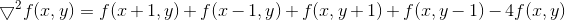
实际：


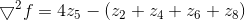
或：


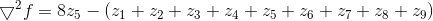
缺点：

1. 拉普拉斯算子对噪声具有敏感性，对噪声有双倍加强作用。
2. 拉普拉斯算子的幅值产生双边缘。
3. 拉普拉斯算子不能检测边缘的方向。

优点：

1. 可以利用零交叉的性质进行边缘定位。
2. 可以确定一个像素是在边缘暗的一边还是亮的一边。
3. 对细线和孤立点检测效果较好。

（f）LoG 检测算子

语法：

[g, t] = edge(f, ‘log’, T, sigma)

拉普拉斯算子与平滑过程一起利用零交叉找到边缘

上式称为高斯型的拉普拉斯算子LoG

分析：

1. 高斯型函数的目的是对图像进行平滑处理。
2. 拉普拉斯算子的目的是提供一幅用零 交叉确定边缘位置的图像。
3. 平滑处理减少了噪声的影响。

Sobel 边缘检测算子的使用

f = imread('D:数字图像处理第十章学习Fig1006(a).tif');     % 图像大小：486×486
subplot(3,2,1),imshow(f),title('(a)原始图像');
[gv, t] = edge(f,'sobel','vertical');
subplot(3,2,2),imshow(gv),title('(b)Sobel模板处理后结果');
gv = edge(f, 'sobel', 0.15, 'vertical');
subplot(3,2,3),imshow(gv),title('(c)使用指定阈值的结果');
gboth = edge(f, 'sobel', 0.15);
subplot(3,2,4),imshow(gboth),title('(d)指点阈值确定垂直边缘和水平边缘的结果');
w45 = [-2 -1 0;-1 0 1; 0 1 2];
g45 = imfilter(double(f), w45, 'replicate');
T = 0.3 * max(abs(g45(:)));
g45 = g45 >= T;
subplot(3,2,5),imshow(g45),title('(e)-45°方向边缘');
f45= [0 1 2;-1 0 1;-2 -1 0];
h45= imfilter(double(f), f45,'replicate');
T = 0.3 * max(abs(h45(:)));
h45 = h45 >= T;
subplot(3,2,6),imshow(h45),title('(f)+45°方向边缘'); 

Sobel、LoG和 Canny边缘检测算子的比较

f = imread('D:数字图像处理第十章学习Fig1006(a).tif');     % 图像大小：486×486
[g_sobel_default,ts] = edge(f,'sobel');
[g_log_default,tlog] = edge(f,'log');
[g_canny_default,tc] = edge(f,'canny');

g_sobel_best = edge(f,'sobel',0.05);
g_log_best = edge(f,'log',0.003,2.25);
g_canny_best = edge(f,'canny',[0.04 0.10],1.5);

subplot(3,2,1);imshow(g_sobel_default);title('(a)默认sobel');
subplot(3,2,2);imshow(g_sobel_best);title('(b)最佳sobel');
subplot(3,2,3);imshow(g_log_default);title('(c)默认LoG');
subplot(3,2,4);imshow(g_log_best);title('(d)最佳LoG');
subplot(3,2,5);imshow(g_canny_default);title('(e)默认canny');
subplot(3,2,6);imshow(g_canny_best);title('(f)最佳canny');

分析：

1. 感兴趣的主要边缘是建筑的角落、窗户、由亮的砖 结构形成的门口和门本身、屋顶线以及围绕建筑且距离地面三分之二的混凝土带。
2. 对于’log’和’canny’选项，sigma的默认值分别是 2.0 和 1.0。除了 Sobel 图像之 外，通过默认值计算得出的图像与想要得到的清晰边缘图相差较远。
3. 由默认值开始，每个选项的参数分别随早些时候提到的显示主要特性的目标而变化，并尽可能减少不必要的细节。
4. 如图(b)所示，Sobel 得出的结果与我们想要的水泥带和门口的左边缘相差还较远。在 (d)中，LoG的结果相比 Sobel 的结果要好一些，比 LoG的默认值得出的结果要好得多。但是，门口的左边缘没有检测出来，建筑物周围水泥带的两个边也还是不够清晰。Canny得出的结果(图(f))到目前为止要远远好于前两种。
5. 特别注意：门口的左边缘已被清晰检测到，还有混凝土带和其他细节，比如门口上方屋顶的通风栅格。除了检测到要求的特征之外，Canny检测算子还产生了最清晰的边缘图。

（二）使用霍夫变换的线检测

霍夫变换可以用于将边缘像素连接起来得到边界曲线，它的主要优点在于受噪声和曲线间断的影响较小。

图像处理工具箱提供了 3 个与霍夫变换有关的函数。
函数 hough 实现霍夫变换的概念。
函数 houghpeaks 寻找霍夫变换中的峰值（高计数累加器单元）。
函数 houghlines 基于前两个函数的结果，提取原始图像中的线段。

2.1 函数hough

语法：

[H, theta, rho] = hough(f)

[H, theta, rho] = hough(f, ‘ThetaRes’, val1, ‘RhoRes’, val2)

H 是霍夫变换矩阵，theta(以度计)和 rho 是 ρ 和 θ 值向量，在这些值上产生霍夫变换。val1是 0 到 90 的标量，指定了沿 θ 轴霍夫变换的间距(默认是 1)，val2 是 0<val2<hypot(size(I,1),size(I,2))的实标量，指定了沿 ρ 轴的霍夫变换的间隔(默认是 1)。

霍夫变换的说明

f = zeros(101, 101);  
f(1, 1) = 1; f(101, 1) = 1; f(1, 101) = 1;  
f(101, 101) = 1; f(51, 51) = 1; 
H = hough(f);imshow(H,[]);
[H, theta, rho] = hough(f);  
imshow(H, [], 'XData', theta, 'YData', rho ,'InitialMagnification', 'fit')  
axis on, axis normal  
xlabel('theta'), ylabel('rho') 

2.2 函数houghpeaks

语法：

peaks = houghpeaks(H, NumPeaks)

peaks = houghpeaks(…, ‘Threshold’, val1, ‘NHoodSize’, val2)

“…”指出来自默认语法和 peaks 的输入是持有峰值行和列坐标的 Q×2 大小的矩 阵。Q的范围是 0 到NumPeaks，H是霍夫变换矩阵。参数val1是非负的标量，指定了 H中 的什么值被考虑为峰值；val1可以从 0 到Inf变化，默认值是0.5*max(H( : ))。参数val2 是奇整数的两元素矢量，指定量围绕峰值的邻域大小。

2.3 函数houghlines

语法：

lines = houghlines(f, theta, rho, peaks)

lines = houghlines(…, ‘FillGap’, val1, ‘MinLength’, val2)

theta和rho是来自函数hough的输出，peaks是函数houghpeaks的输出。输出lines是结构数组，长度等于找到的线段数。结构中的每个元素可以看成一条线，并含有下列字段：

1. point1：两元素向量[r1, c1]，指定了线段终点的行列坐标。
2. point2：两元素向量[r2, c2]，指定了线段其他终点的行列坐标。
3. theta：与线相关的霍夫变换的以度计量的角度。
4. rho：与线相关的霍夫变换的ρ轴位置。
5. val1：是正的标量，指定了与相同的霍夫变换相关的两条线段的距离。当两条线段之间的距离小于指定的值时，函数houghlines把线段合并为一条线段(默认的距离是20个像素)。
6. val2：是正的标量，指定合并的线是保留还是丢弃。如果合并的线比val2指定的值短，就丢弃(默认值是40)。

用霍夫变换检测和连接线

在这个例子中，我们用函数hough、houghpeaks和houghlines寻找二值图像f的一组线段。首先，我们用比默认值更好的角间距(用0.2代替1.0)计算和显示霍夫变换：

f = imread('D:数字图像处理第十章学习Fig1006(a).tif');    
[H, theta, rho] = hough(f, 'ThetaResolution', 0.2);  
imshow(H, [], 'XData', theta, 'YData', rho, 'InitialMagnification', 'fit') 
axis on, axis normal  
xlabel('theta'), ylabel('rho') 
peaks = houghpeaks(H, 5);  
hold on  
plot(theta(peaks(:, 2)), rho(peaks(:, 1)), ...  
         'linestyle', 'none', 'marker', 's', 'color', 'w');title('(a)带有已选择的5个峰值位置的霍夫变换');  
lines = houghlines(f, theta, rho, peaks);  
figure, imshow(f), hold on  
for k = 1:length(lines)  
xy = [lines(k).point1 ; lines(k).point2];  
plot(xy(:,1), xy(:,2), 'LineWidth', 4, 'Color', [.8 .8 .8]); title('(b)与霍夫变换峰值对应的线段 ');   
end 

（三）阈值处理

3.1 基本全局阈值处理

基于图像数据自动地选择阈值算法：

(1) 针对全局阈值选择初始估计值T。
(2) 用T 分割图像。这会产生两组像素：G1 由所有灰度值大于T 的像素组成，G2 由所有灰度值小于等于T 的像素组成。
(3) 分别计算G1、G2 区域内的平均灰度值m1 和m2。
(4) 计算出新的阈值：

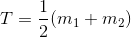
(5) 重复步骤(2)～(4)，直到在连续的重复中，T 的差异比预先设定的参数△T 小为止。
(6) 使用函数im2bw 分割图像：

g = im2bw(f, T/den)

其中，den 是整数(例如一幅8 比特图像的255)，是T/den 比率为1 的数值范围内的最大值，正如函数im2bw 要求的那样。

计算全局阈值：

f = imread('D:数字图像处理第十章学习Fig1013(a).tif');    
count=0;
T=mean2(f);
done=false;
while ~done
 count=count+1;
 g=f>T;
 Tnext=0.5*(mean(f(g))+mean(f(~g)));
 done=abs(T-Tnext)<0.5;
 T=Tnext;
end
disp('count的值为：');
disp(['count=',num2str(count)]) %打印输出count的值
disp('T的值为：');
disp(['T=',num2str(T)])  %打印输出T的值
g=im2bw(f,T/255);
figure;subplot(1,3,1);imshow(f);title('(a)带噪声的指纹');
subplot(1,3,2);imhist(f);title('(b)直方图');
subplot(1,3,3);imshow(g);title('(c)用全局阈值分割的结果');

3.2 使用 Otsu’s 方法的最佳全局阈值处理

Otsu算法：取一个最优阈值把原图像分为前景色（A部分）与背景色（B部分），两部分的类间方差越大，说明两部分差别越大，便能有效的分割图像。所以该算法最关键的是找到最优阈值。

语法：

[T, SM] = graythresh(f)

f是输入图像，T是产生的阈值并被规一化到[0,1]中，SM是可分性度量。

f = imread('D:数字图像处理第十章学习Fig1014(a).tif');    
count=0;
T=mean2(f);
done=false;
while ~done
 count=count+1;
 g=f>T;
 Tnext=0.5*(mean(f(g))+mean(f(~g)));
 done=abs(T-Tnext)<0.5;
 T=Tnext;
end
disp('count的值为：');
disp(['count=',num2str(count)]) %打印输出count的值
disp('T的值为：');
disp(['T=',num2str(T)])  %打印输出T的值
g=im2bw(f,T/255);

[T, SM] = graythresh(f);
 g1 = im2bw(f, T); 
figure;subplot(2,2,1);imshow(f);title('(a)带噪声的指纹');
subplot(2,2,2);imhist(f);title('(b)直方图');
subplot(2,2,3);imshow(g);title('(c)用全局阈值分割的结果');
subplot(2,2,4);imshow(g1);title('(d)使用 Otsu s算法得到的结果 ');

3.3 使用图像平滑改进全局阈值处理

噪声会把简单的阈值处理问题变为不能解决的问题。当不能再源头降低噪声且阈值处理是所选择的分割方法时，增强性能的一种常用技术是在阈值处理前先对图像进行平滑。

f = imread('D:数字图像处理第十章学习Fig1015(a)[noiseless].tif');    
fn = imnoise(f,'gaussian',0,0.038);
subplot(2,3,1),imshow(fn);title('(a) 带噪图像');
subplot(2,3,2),imhist(fn);title('(b) 直方图');
Tn = graythresh(fn);
gn = im2bw(fn,Tn);
subplot(2,3,3),imshow(gn);title('(c)用 Otsu s 方法得到的结果');
w = fspecial('average',5);
fa = imfilter(fn,w,'replicate');
subplot(2,3,4),imshow(fa);title('(d)用 5×5 均值模板平滑后的图像');
subplot(2,3,5),imhist(fa);title('(e) 直方图');
Ta = graythresh(fa);
ga = im2bw(fa,Ta);
subplot(2,3,6),imshow(ga);title('(f)使用 Otsu s 方法的阈值处理后的结果');

3.4 使用边缘改进全局阈值处理

当物体比背景小得多时，他们对直方图的贡献可以或略不计，使用边缘信息可以改进这种情况。

算法：
1.计算一副边缘图像（梯度和拉普拉斯都可以）。
2.指定一个阈值T。
3.用步骤2中的阈值对步骤1中产生的图像进行阈值处理，产生一副二值图像gT(x,y)。在从f(x,y)中选取对应于强边缘像素的下一步中，该图像作为一副模板图像
4.仅用f(x,y)中对应于gT(x,y)中像素为1的位置的像素计算直方图。
5.用步骤4中的直方图全局地分割f(x,y)。

通常指定对应于一个百分位的 T 值，它通常设置一个高值（如第90个百分位），以便边缘图像中只有很少的像素用于阈值的计算。

自定义函数 percentile2i 可实现这一目的。该函数计算一个灰度值 I，它对应于一个指定的百分位 P。语法为:

I = percentile2i(h, P)

1. h 是图像的直方图
2. P 是区间 [0, 1] 内的百分位值
3. I 是对应于第 P 个百分位的灰度级

f = tofloat(imread('D:数字图像处理第十章学习Fig1017(a).tif'));    
subplot(2,3,1),imshow(f);title('(a) 酵母细胞的图像');
subplot(2,3,2),imhist(f);title('(b) 直方图');
hf = imhist(f); 
[Tf SMf] = graythresh(f); 
gf = im2bw(f, Tf); 
subplot(2,3,3),imshow(gf);title('(c) 用函数graythresh对(a)进行分割');
w = [-1 -1 -1; -1 8 -1; -1 -1 -1]; 
lap = abs(imfilter(f, w, 'replicate')); 
lap = lap/max(lap(:)); 
h = imhist(lap);
Q = percentile2i(h, 0.995); 
markerImage = lap > Q; 
fp = f.*markerImage; 
subplot(2,3,4),imshow(fp);title('(d) 标记图像与原始图像的乘积');
hp = imhist(fp);
hp(1) = 0;
subplot(2,3,5),bar(hp,0) ;title('(e)(d)中非0像素的直方图');
T = otsuthresh(hp);
g = im2bw(f, T); 
subplot(2,3,6),imshow(g);title('(f)用 Otsu s 方法进行阈值处理后的图像');

3.5 基于局部统计的可变阈值处理

在不规则光照情形下，或者在有多个主要物体灰度的情况下（此时全局阈值处理有困难），进行补偿的一种方法是采用可变阈值处理。

计算局部标准差，使用函数 stdfilt：

g = stdfilt(f, nhood)

nhood 是由 0 和 1 组成的数组，其中非零元素指定用于计算局部标准差所用的领域。nhood 的尺寸在每个维度上必须是奇数，默认值是 ones(3)。

对全局和局部阈值处理的比较 ：

f = tofloat(imread('D:数字图像处理第十章学习Fig1017(a).tif'));    
subplot(2,2,1),imshow(f);title('(a) 酵母细胞的图像');
[TGlobal] = graythresh(f); 
gGlobal = im2bw(f, TGlobal); 
subplot(2,2,2),imshow(gGlobal);title('(b)用 Otsus 方法分割的图像');
g = localthresh(f, ones(3), 30, 1.5, 'global'); 
SIG = stdfilt(f, ones(3));
subplot(2,2,3), imshow(SIG, [ ]) ;title('(c) 局部标准差图像');
subplot(2,2,4),imshow(g);title('(d)  用局部阈值处理分割的图像 ');

分析：

1. 从背景中分割出细胞来，并且从细胞的主体分出细胞核(内部的亮区域)。这幅图像中有三个主要的灰度级，因此有理由期待这样的分割是可能的。
2. 因为细胞核比细胞本身明显较亮，所以预期围绕细胞核边界的标准差相对较大，而围绕细胞边界的标准差稍微小一些。如图©所示，的确是这种情况。由此得出以下结论：在基于 局部标准差的函数localthresh中，这应该是很有帮助的。
3. 如图 (d)所示，运用了属性的分割是相当有效的。个别细胞已经从背景中分割出来了， 并且细胞核也被完全分割出来了。
4. 当背景接近于常数，并且所有物体的灰度高于或低于背景灰度时，选择全局均值一般会得到较好的结果。

3.7 使用移动平均的图像阈值处理

f = tofloat(imread('D:数字图像处理第十章学习Fig1019(a).tif'));    
subplot(1, 2, 1);imshow(f);title('(a)由斑点阴影污染了的文本图像');
T = graythresh(f);
g1 = im2bw(f, T);
g2 = movingthresh(f, 20, 0.5);
subplot(1, 2, 2); imshow(g2);title('(b)用移动平均进行局部阈值处理的结果');

（四）基于区域的分割

4.1 区域生长

区域生长：根据预先定义的生长准则将像素或子区域组合为更大的区域的过程。

基本方法是从一组 “种子” 点开始，将与种子性质相似的那些邻域像素附加到每个种子上来形成这些生长区域。

语法：

[g, NR, SI, TI] = regiongrow(f, S, T)

1. S： 可以是一个数组（与 f 大小相同）或一个标量。若 S 是一个数组，则它在种子点的所有坐标处必须包含 1，而在其他地方包含 0。如果 S 是一个标量，则它定义一个灰度值，那么 f 中具有该值的所有点都会成为种子点。
2. T： 可以是一个数组或一个标量。若 T 是一个数组，则它对 f 中的每个位置包含一个阈值。若 T 是一个标量，则它定义一个全局阈值。S 和 T 所有值必须标定到区间 [0, 1]，且与输入图像的类无关。
3. g： 是分割后的图像。
4. NR： 是所找到的区域的数量。
5. SI： 是包含种子点的一幅图像。
6. TI： 是包含处理连接性前就已通过阈值测试的像素的一幅图像。

使用区域生长检测焊接空隙

f = imread('D:数字图像处理第十章学习Fig1020(a).tif');    
subplot(2,2,1),imshow(f);
title('(a)显示有焊接缺陷的图像');
%函数regiongrow返回的NR为是不同区域的数目，参数SI是一副含有种子点的图像
%TI是包含在经过连通前通过阈值测试的像素
[g,NR,SI,TI]=regiongrow(f,1,0.26);%种子的像素值为255，65为阈值
subplot(2,2,2),imshow(SI);
title('(b)种子点');
subplot(2,2,3),imshow(TI);
title('(c)通过了阈值测试的像素的二值图像(白色)');
subplot(2,2,4),imshow(g);
title('(d)对种子点进行8连通分析后的结果');

分析：

1. 图(a)显示了一幅包含几个裂缝(水平的暗区域)和空隙(穿过图像中部的、亮的、白色的 水平方向条纹)的 X射线焊接图像。望使用regiongrow函数来分割相应的焊接缺陷区 域。这些被分割的区域可以用于自动检测这一任务，可以用于包含历史研究的数据库，也可以用于控制自动焊接系统。
2. 图(b)显示了种子点(图像 SI)。在这种情况下，种子点很多，因为种子被指定为在图 像中具有数值 225 的所有点(标定后是1)。
3. 图 ( c)是图像 TI，显示了所有通过阈值测试的 点；也就是说，具有灰度 Zi 且满足︱Zi –S︱≤T 的点。
4. 图 (d)显示了提取图 ( c)中所有连接到种子点的像素的结果。这是分割后的图像 g。通过将这幅图像与原始图像进行比较，区域生长过程确实以合理的精确度分割了焊接的缺陷这一点是很明显的。

4.2 区域分离和聚合

将一幅图像细分为一组任意的不相交区域，然后聚合或分离这些区域。过程如下：

1. 令 R 表示整幅图像区域，选择一个属性 P。将满足 P($R_i$)=False 的任何区域 $R_i$ 分离为 4 个不相交的象限区域。
2. 当不可能进一步分离时，聚合满足条件 P($R_i$ u $R_j$) = True 的任意两个相邻区域 $R_i$，$R_j$ 。
3. 当无法进一步聚合时，停止操作。

工具箱中实现四叉树分解的函数是 qtdecomp。

Z = qtdecomp(f, @split_test, parameters)

1. Z 是包括四叉树结构的一个稀疏矩阵。若 Z(k, m) 是非零的，则 Z(k, m) 是分解的一个块的左上角，且该块的大小是 Z(k, m) 。
2. split_test 用于确定一个区域是否进行分离。

函数 qtgetblk 可得到四叉树分解中的实际四分区域像素值。

[vals, r, c] = qtgetblk(f, Z, m)

1. vals 是一个数组，包含 f 的四叉树分解中的尺寸为 m*m 的块的值。
2. Z 是由 qtdecomp 返回的稀疏矩阵。
3. r, c 是包含块的左上角的行坐标和列坐标的向量。

下面是一个基本的分离、聚合函数，说明 qtdecomp 的用法。

g = splitmerge(f, mindim, @predicate)

1. g 是输出图像，输出图像每个连接区域都使用不同的整数标注。
2. mindim 定义分解中允许的最小块尺寸，必须是 2 的正整数次幂。

flag = predicate(region)

如果在 region 区域中的像素满足函数中由代码定义的属性，那么函数就必须写成返回 true 的形式，否则，flag 的值就必须是false。

f = imread('D:数字图像处理第十章学习Fig1023(a).tif');    
subplot(2,3,1),imshow(f);
title('(a)区域分割原始图像');
g64=splitmerge(f,64,@predicate);%64代表分割中允许最小的块
subplot(2,3,2),imshow(g64);
title('(b)mindim为64时的分割图像');
g32=splitmerge(f,32,@predicate);%32代表分割中允许最小的块
subplot(2,3,3),imshow(g32);
title('(c)mindim为32时的分割图像');
g16=splitmerge(f,16,@predicate);%16代表分割中允许最小的块
subplot(2,3,4),imshow(g16);
title('(d)mindim为16时的分割图像');
g8=splitmerge(f,8,@predicate);%8代表分割中允许最小的块
subplot(2,3,5),imshow(g8);
title('(e)mindim为8时的分割图像'); 
g4=splitmerge(f,4,@predicate);%4代表分割中允许最小的块
subplot(2,3,6),imshow(g4);
title('(f)mindim为4时的分割图像');

分析：

1. 图 (a)显示了一幅天鹅星座环的 X 射线频段图像。图像的大小为 256×256 像素。该例的目的是分割出环绕致密中心的稀疏环。
2. 图 (b)到(f)显示了使用函数splitmerge且mindim的值分别等于 64、32、16、8、4 时分割图(a)的结果。所有图像均显示了边界的细节水平与 mindim 的值成反比的分割结果。
3. 图中的所有结果都是合理的分割。如果以除原始图像之外的这些图像之一作为模板提取感兴趣区域，图(d)的结果将是最好的选择，因为它是具有最多细节的实心区域。

（五）使用分水岭变换的分割

分水岭变换将找到灰度图像中的集水盆地和脊线。集水盆地就是我们要识别的物体或区域。

5.1 使用距离变换的分水岭分割

二值图像的距离变换是每个像素到最接近非零像素的距离。

使用距离变换和分水岭变换分割二值图像 ：

f = tofloat(imread('D:数字图像处理第十章学习Fig1017(a).tif'));
g=im2bw(f,graythresh(f));   %把图像转换为二值图像
subplot(2,3,1),imshow(f);title('(a)使用距离和分水岭分割原图');
subplot(2,3,2),imshow(g);title('(b)原图像阈值处理后的图像');
gc=~g;   %对图像求补
subplot(2,3,3),imshow(gc),title('(c)阈值处理后取反图像');
D=bwdist(gc);   %计算其距离变换
subplot(2,3,4),imshow(D),title('(d)使用距离变换后的图像');
L=watershed(-D);   %计算负距离变换的分水岭变换
w=L==0;    %L 的零值即分水岭的脊线像素
subplot(2,3,5),imshow(w),title('(e)距离变换后的负分水岭图像');
g2=g & ~w;   %原始二值图像和图像 w 的 “补” 的逻辑 “与” 操作可完成分割
subplot(2,3,6),imshow(g2),title('(f)阈值图像与分水岭图像相与图像');

分析：

1. 使用im2bw和graythreshi把图像变换为二值图像，图 (a)显示了结果。
2. 对图像求补，计算距离变换。然后，用函数watershed 计算距离变换的负分水岭变换。其中，L 是标记矩阵。A 是输入数组(一般可以是任何维数，但在本章是二维)，并且conn指定了连通性(对于二维数组是 4 或 8(默认值))。
3. 在L中，正整数与汇水盆地相对应，零值指出分水岭的脊线像素，图(b)和( c)显示了求补后的图像及其距离变换。因为L的 0 值像素是分水岭的脊线像素，图中仅显示这些像素。分水岭的脊线图像显示于图(d)中。
4. 最后，使用原始的二值图像和图像w的“补”，通过逻辑 AND操作完成分割，如图 (e)所示，图(e)中的某些物体没有很好地分开。这被称为过分割，这是使用基于分水岭的分割方法时常常会出现的问题。

5.2 使用梯度的分水岭分割

在使用针对分割的分水岭变换之前，常常使用梯度幅度对图像进行预处理。梯度幅度图像沿着物体的边缘有较高的像素值，而在其他地方则有较低的像素值。在理想的情况下，分水岭变换可得到沿物体边缘的分水岭脊线。

使用梯度和分水岭变换分割灰度图像 ：

f = tofloat(imread('D:数字图像处理第十章学习Fig1023(a).tif'));
subplot(2,2,1),imshow(f);
title('(a)使用梯度和分水岭变换分割灰度图像');
h=fspecial('sobel');
fd=double(f);
g=sqrt(imfilter(fd,h,'replicate').^2+imfilter(fd,h','replicate').^2); %计算图像的幅度梯度
subplot(2,2,2),imshow(g,[]);
title('(b)使用梯度和分水岭分割幅度图像');
L=watershed(g);
wr=L==0;
subplot(2,2,3),imshow(wr);
title('(c)对梯度复制图像进行二值分水岭后图像');
g2=imclose(imopen(g,ones(3,3)),ones(3,3));
L2=watershed(g2);   %计算梯度的分水岭变换，并找到分水岭脊线。
wr2=L2==0;
f2=f;
f2(wr2)=255;
subplot(2,2,4),imshow(f2);
title('(d)平滑梯度图像后的分水岭变换');

分析：

1. 图( c)所示，这是不太好的分割结果；有太多的与我们感兴趣的物体边界不相对应的分水岭脊线。这是过分分割的另一个例子。针对这一问题的解决方法是在计算分水岭变换之前先平滑梯度图像。
2. 图 (d)显示了叠加结果。虽然增强图©的目的达到了，但仍然存在一些附加的脊线，对于决定哪些汇水盆地真正与感兴趣物体有关还是很困难。

5.3 控制标记符的分水岭分割

由于噪声和梯度的其他局部不规则性，常会导致过分分割。一种方法是基于标记符修改梯度图像。标记符是属于一幅图像的连通分量。

标记符控制的分水岭分割示例 :

f = imread('D:数字图像处理第十章学习Fig1028(a).tif');
h=fspecial('sobel');
fd=double(f);
g=sqrt(imfilter(fd,h,'replicate').^2+imfilter(fd,h','replicate').^2);
L=watershed(g);
wr=L==0;
figure,subplot(2,3,1),imshow(wr,[]);
title('(a)控制标记符的分水岭分割幅度图像');
rm=imregionalmin(g);%梯度图像有很多较浅的坑，造成的原因是原图像不均匀背景中灰度细小的变化
subplot(2,3,2),imshow(rm,[]);
title('(b)对梯度幅度图像的局部最小区域');
im=imextendedmin(f,2);%得到内部标记符
fim=f;
fim(im)=175;
subplot(2,3,3),imshow(f,[]);
title('(c)内部标记符');
Lim=watershed(bwdist(im));
em=Lim==0;
subplot(2,3,4),imshow(em,[]);
title('(d)外部标记符');
g2=imimposemin(g,im | em);
subplot(2,3,5),imshow(g2,[]);
title('(e)修改后的梯度幅度值');
L2=watershed(g2);
f2=f;
f2(L2==0)=255;
subplot(2,3,6),imshow(f2),title('(f)最后分割的结果');

分析：

1. 在图(a)中可以看到，结果严重地过分割了。一部分是由于存在大量的小区域。
2. 图(b)显示的多数局部小区域的位置非常浅，并且表现的细节与我们的分割问题不相干。
3. 用函数imextendedmin来得到内部标记符的集合,最后将灰斑点的最小区域位置叠加在原始图像上，如图©所示。可以看到，得到的斑点的确很合理地标记了我们想要分割的物体。
4. 图 (d)显示了二值图像em中的分水岭脊线。因为这些脊线位于由im标记的暗斑点 间，所以它们应该是很好的外部标记符。
5. 通过在内部和外部标记符的位置覆盖局部最小区域，可以改进梯度图像，图(e)显示了结果。
6. 在原始图像上叠加分水岭脊线,得到一个有很大改进的分割结果如图(f)所示。

最后

以上就是瘦瘦蜜蜂为你收集整理的数字图像处理第十章——图像分割数字图像处理—图像分割的全部内容，希望文章能够帮你解决数字图像处理第十章——图像分割数字图像处理—图像分割所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。