我是靠谱客的博主 缥缈火车,这篇文章主要介绍《MATLAB专刊》——利用向量化编程提升MATLAB代码执行效率1. 实验说明2. 实验结果3. 源程序4. 参考资料,现在分享给大家,希望可以做个参考。
文章目录
- 1. 实验说明
- 2. 实验结果
- 3. 源程序
- 3.1 绘图源程序
- 3.2 测试源程序
- 4. 参考资料
为了阐明采用向量化编程思路对于MATLAB双重 f o r for for循环优化的效果,本文通过一个实例展示不同编程思路对于代码执行效率的影响( B站视频讲解版)。
1. 实验说明
-
试验组别:
- 分为双重循环、向量化编程(Repmat函数)、向量化编程(Meshgrid函数)、向量化编程(bsx函数)共四个组别,每个组别重复 10 10 10次。 测试规模:
- 从2500万到52500万,以间隔为125000为步长 测试环境:
-
硬件: Intel®Core™ i9-10940X 双核CPU@3.30GHz 3.31 GHz,128GB内存
软件:Windows 10 系统, MATLAB R2018a
2. 实验结果
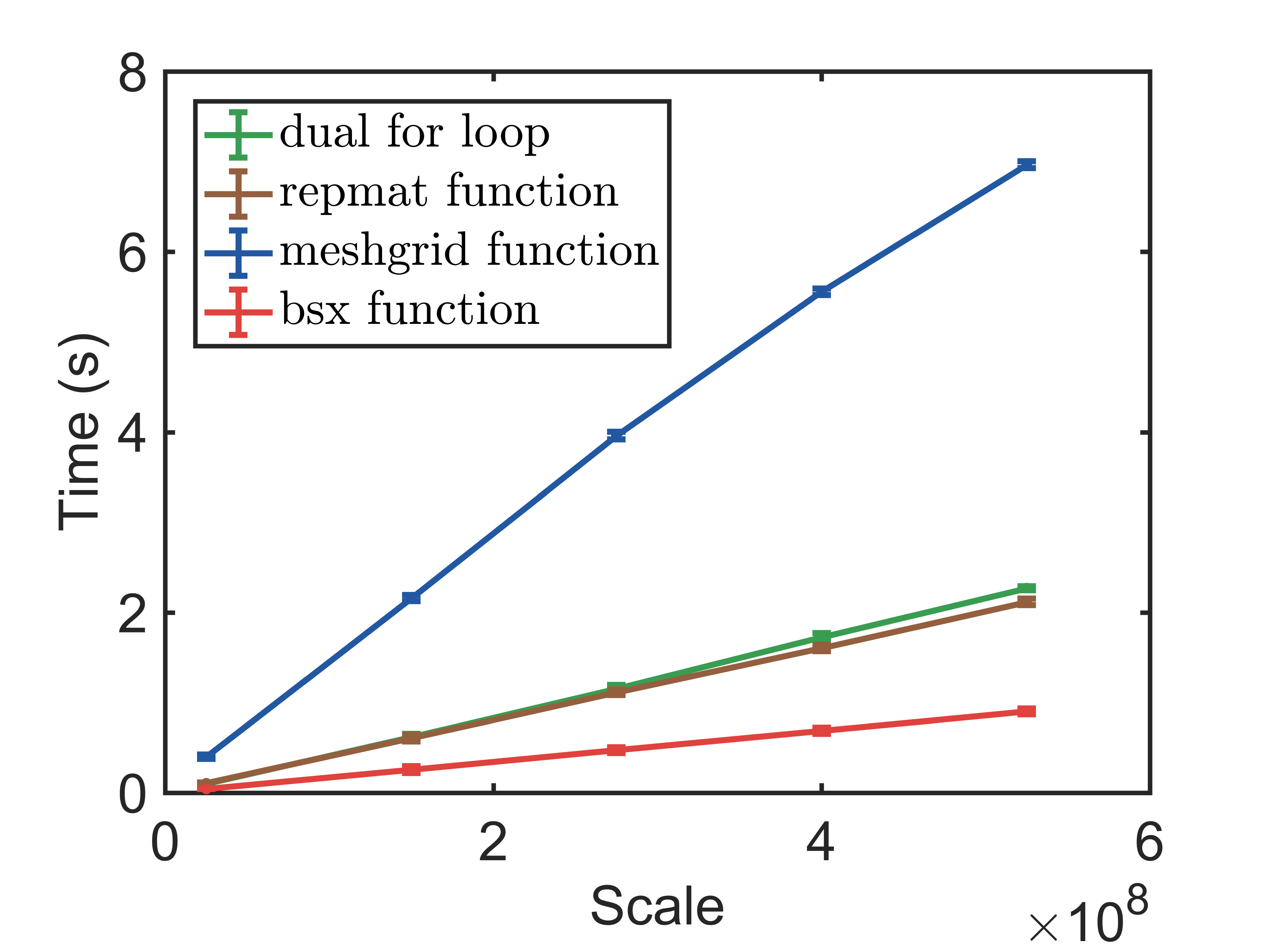 图1 实验结果对比图 图1 实验结果对比图
|
|
|
| 测试规模 | 双重for循环用时(s) | repmat函数用时(s) | meshgrid函数用时(s) | bsx函数用时(s) |
|---|---|---|---|---|
| 25,000,000 | 0.102±0.011 | 0.107±0.005 | 0.399±0.024 | 0.044±0.001 |
| 150,000,000 | 0.619±0.034 | 0.608±0.039 | 2.160±0.034 | 0.257±0.038 |
| 275,000,000 | 1.156±0.040 | 1.115±0.032 | 3.963±0.041 | 0.473±0.033 |
| 400,000,000 | 1.727±0.045 | 1.606±0.035 | 5.558±0.035 | 0.688±0.033 |
| 525,000,000 | 2.269±0.021 | 2.117±0.036 | 6.965±0.038 | 0.903±0.033 |
- 从图 1 1 1和表格 1 1 1可以看出,代码执行效率方面: m e s h g r i d 函 数 < 双 重 f o r 循 环 < r e m p a t 函 数 < b s x 函 数 meshgrid函数<双重for循环<rempat函数<bsx函数 meshgrid函数<双重for循环<rempat函数<bsx函数。
- b s x bsx bsx函数执行效率最高,几乎是 m e s h g r i d meshgrid meshgrid的 6 − 10 6-10 6−10倍,是双重 f o r for for循环的两倍。令人感到意外的是,采用向量化编程的 r e p m a t repmat repmat并没有比双重 f o r for for循环快很多,在测试实验中,两者相差并不是很大(详细可参考表1的实验结果)。
- 上层封装函数的执行效率显著低于底层函数,隐式运算的速度显著快于显式运算。
3. 源程序
本节附录了测试的源程序
3.1 绘图源程序
clc
clear all
close all
path = '测试结果总表.xlsx'; % 文件路径
%% 1. 读取数据
sheetname = '测试结果'; % excel页名称
[number,txt,raw] = xlsread(path,sheetname);
d.scale = number(:,1); % 测试规模
%% 2. 绘图
close all
Mycolor = [57,157,81;
148,95,63;
34,88,161;
224,66,61]/255; % 绿棕蓝红
Mysize = [1.5;
1.5;
18]; % 线宽设置
% Mystyle = ['o';
% '^';
% 's';
% 'p'];
figure
for i = 1:4
d.time = number(:,2*i); % 测试时长(s)
d.var = number(:,2*i+1); % 均方差
h = errorbar(d.scale,d.time,d.var,'.-','Color',Mycolor(i,:),'LineWidth',2,...
'MarkerSize',12);
% set(h,'Marker',Mystyle(i));
hold on
end
%% 3. 图表美化
set(gca,'LineWidth',Mysize(2),'FontSize',Mysize(3),'FontName','Arial')
xlabel('Scale','FontName','Arial','FontSize',Mysize(3)); % x标签
ylabel('Time (s)','FontName','Arial','FontSize',Mysize(3)); % y标签
legend({'dual for loop','repmat function','meshgrid function','bsx function'},...
'Interpreter','latex','location','NorthWest'...
,'FontName','Arial','FontSize',Mysize(3)-2) % 添加图例
% print(gcf,'-clipboard','-dmeta')
print(gcf,'-r600','-dpng','测试对比结果') % 保存图片到指定路径
3.2 测试源程序
双重for循环:
clc
clear all
close all
%% 双重for循环
S = [1000:5000:25000];
ResultsWrite = zeros(length(S)^2,2); % 初始化,第一列-计算规模,第二列-计算时间(10次平均值),第三列均方差
flag = 0;
for k1 = 1:length(S)
for k2 = 1:10
flag = flag + 1; % 计数
s = S(k1); t = 25000;
%% 测试段-开始
t0 = clock; % 获取当前系统时间
E = zeros((s-1)*(t-1),1); % 初始化网格矩阵
N = 0; % 网格计数
for i = 1:s-1
for j = 1:t-1
N = N + 1; % 计数
E(N) = (j-1)*(s-1) + i; % 单元编号
end
end
ResultsWrite(flag,:) = [s*t,etime(clock,t0)]; % 程序运行时间
%% 测试段-结束
end
end
name = strcat('双重循环运行时间记录','.xlsx'); % 保存文件名
Results = sortrows(ResultsWrite,1); % 排序
regResult = reshape(Results,10,10); % 规整化
A = mean(regResult,1); % 求均值
B = std(regResult,0,1); % 求均方差
B1 = B';
B2 = B1(6:10); % 均方差列向量
finRes = [reshape(A,5,2),B2];
xlswrite(name,finRes); % 保存文件为excel
repmat函数:
clc
clear all
close all
%% 向量化编程(repmat函数)
S = [1000:5000:25000];
ResultsWrite = zeros(length(S)^2,2); % 初始化,第一列-计算规模,第二列-计算时间(10次平均值),第三列均方差
flag = 0;
for k1 = 1:length(S)
for k2 = 1:10
flag = flag + 1; % 计数
s = S(k1); t = 25000;
%% 测试段-开始
t0 = clock; % 获取当前系统时间
E = zeros((s-1)*(t-1),1); % 初始化网格矩阵
I = [1:s-1]'; J = [1:t-1]'; % 向量化
E = (s-1).*repmat((J-1),1,s-1) + repmat(I',t-1,1); % 单元编号
ResultsWrite(flag,:) = [s*t,etime(clock,t0)]; % 程序运行时间
%% 测试段-结束
end
end
name = strcat('向量化编程(repmat)运行时间记录','.xlsx'); % 保存文件名
Results = sortrows(ResultsWrite,1); % 排序
regResult = reshape(Results,10,10); % 规整化
A = mean(regResult,1); % 求均值
B = std(regResult,0,1); % 求均方差
B1 = B';
B2 = B1(6:10); % 均方差列向量
finRes = [reshape(A,5,2),B2];
xlswrite(name,finRes); % 保存文件为excel
Meshgrid函数:
clc
clear all
close all
%% 向量化编程(meshgrid函数)
S = [1000:5000:25000];
ResultsWrite = zeros(length(S)^2,2); % 初始化,第一列-计算规模,第二列-计算时间(10次平均值),第三列均方差
flag = 0;
for k1 = 1:length(S)
for k2 = 1:10
flag = flag + 1; % 计数
s = S(k1); t = 25000;
%% 测试段-开始
t0 = clock; % 获取当前系统时间
E = zeros((s-1)*(t-1),1); % 初始化网格矩阵
I = [1:s-1]'; J = [1:t-1]'; % 向量化
E = (s-1)*meshgrid(J'-1,I)' + meshgrid(I,J); % 单元编号
ResultsWrite(flag,:) = [s*t,etime(clock,t0)]; % 程序运行时间
%% 测试段-结束
end
end
name = strcat('向量化编程(meshgrid)运行时间记录','.xlsx'); % 保存文件名
Results = sortrows(ResultsWrite,1); % 排序
regResult = reshape(Results,10,10); % 规整化
A = mean(regResult,1); % 求均值
B = std(regResult,0,1); % 求均方差
B1 = B';
B2 = B1(6:10); % 均方差列向量
finRes = [reshape(A,5,2),B2];
xlswrite(name,finRes); % 保存文件为excel
bsx函数:
clc
clear all
close all
%% 向量化编程(bsx函数)
S = [1000:5000:25000];
ResultsWrite = zeros(length(S)^2,2); % 初始化,第一列-计算规模,第二列-计算时间(10次平均值),第三列均方差
flag = 0;
for k1 = 1:length(S)
for k2 = 1:10
flag = flag + 1; % 计数
s = S(k1); t = 25000;
%% 测试段-开始
t0 = clock; % 获取当前系统时间
E = zeros((s-1)*(t-1),1); % 初始化网格矩阵
I = [1:s-1]'; J = [1:t-1]'; % 向量化
E = bsxfun(@plus,(s-1).*(J-1),I'); % 单元编号
ResultsWrite(flag,:) = [s*t,etime(clock,t0)]; % 程序运行时间
%% 测试段-结束
end
end
name = strcat('向量化编程(bsx函数)运行时间记录','.xlsx'); % 保存文件名
Results = sortrows(ResultsWrite,1); % 排序
regResult = reshape(Results,10,10); % 规整化
A = mean(regResult,1); % 求均值
B = std(regResult,0,1); % 求均方差
B1 = B';
B2 = B1(6:10); % 均方差列向量
finRes = [reshape(A,5,2),B2];
xlswrite(name,finRes); % 保存文件为excel
4. 参考资料
MATLAB-基础画图meshgrid
matlab学习笔记 bsxfun函数
matlab函数之bsxfun
Optimizing matlab code which uses repmat
MATLAB编程(3)——MATLAB依次运行多个脚本.m文件
Matlab绘制误差棒图----errorbar函数的使用
【Matlab】如何绘制errorbar误差棒
最后
以上就是缥缈火车最近收集整理的关于《MATLAB专刊》——利用向量化编程提升MATLAB代码执行效率1. 实验说明2. 实验结果3. 源程序4. 参考资料的全部内容,更多相关《MATLAB专刊》——利用向量化编程提升MATLAB代码执行效率1.内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复