文章目录
- 一、什么是堆?
- 1. 堆和数组
- 2. 大根堆和小根堆
- 二、 heapinsert函数
- 1. 手推一轮heapinsert
- 2. 使用heapinsert得到一个大根堆
- 三、heapify函数
- 1. 手推一轮heapify
- 2. 使用heapify整理数组成为一个大根堆
- 四、heapinsert和heapify形成大根堆的时间复杂度
- 五、手推堆排序
- 六、堆排序代码
一、什么是堆?
堆其实就是用数组实现的二叉树,它是利用完全二叉树的结构来维护一组数据。这使得它每进行一组相关操作的时间复杂度为O(1)~O(logN)之间,是相当的有优势哇。
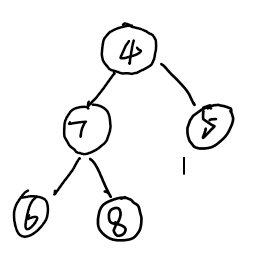
那么什么是完全二叉树呢?我们来看这样一组图:
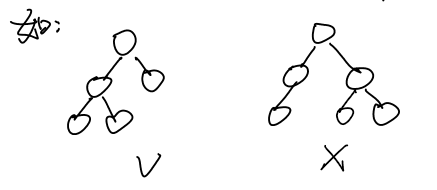
完全二叉树其实就是指高为h的二叉树中前h-1层是满的,最后一层的节点连续集中在最左边。如上图中,你能分辨出来吗?左图为一个完全二叉树,右图则只是一个普通的二叉树。
1. 堆和数组
我们说堆其实是用数组实现的二叉树,其实就是因为堆是一个完全二叉树,它的节点下标是连续的,如下图,我们给出一个数组和该数组形成的堆之间的对应关系。
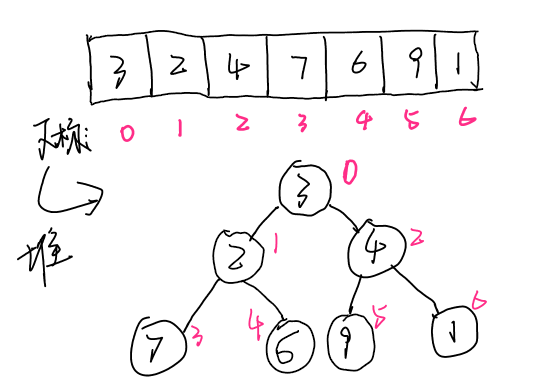
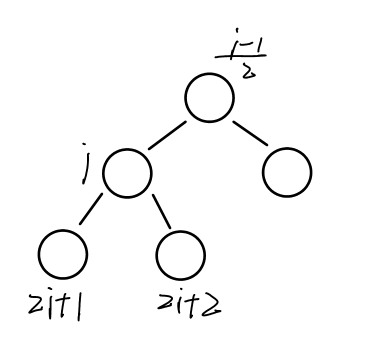
我们需要注意堆中结点下标与其左孩子、右孩子、父节点下标关系:某节点下表为i,则它的左孩子为2i+1,右孩子为2i+2,父节点为(i-1)/2。
2. 大根堆和小根堆
大根堆:顾名思义就是堆顶元素最大
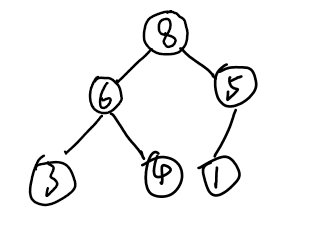
小根堆:堆顶元素最小
二、 heapinsert函数
1. 手推一轮heapinsert
heapinsert功能:已经存在一个是大根堆/小根堆的堆时,重新插入一个新的元素至堆尾,将该元素整理进这个堆中重新形成大根堆/小根堆。
主要思想:将新元素插入堆尾,将其与其父节点进行比较,若比父节点大就进行交换,再将其与其目前的父节点进行比较,若比父节点大则进行交换…直至该元素没有父节点大时停止交换;
如下:目前堆中元素为{7,6,3,5,},我们将元素7插入这个大根堆中。过程如下:
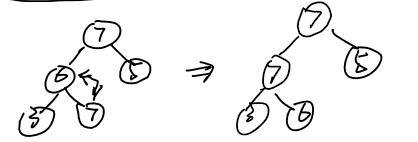
将7插入堆尾,该元素和它的父节点进行比较,由于它比它的父节点大,于是和它的父节点进行交换,来到右图的结构,再与此时他所处的位置的父节点进行交换,此时没有他的父节点大,不再进行交换,调整结束,此时的堆重新构成大根堆。
伪代码如下:
void heapinsert(int *a,int heapsize){
int i = heapsize;
while(a[i] > a[(i-1)/2]){
swap(&a[i],&a[(i-1)/2]);//交换元素
i = (i-1)/2;
}
}
2. 使用heapinsert得到一个大根堆
我们如果将数组中的元素看作一个一个插入一个大根堆,最开始时是一个空堆,然后将第一个元素插入这个堆中,进行heapinsert整理成为一个大根堆,依次将数组中其他元素插入这个堆中。其实就是每个数组的元素都进行了一次heapinsert。
不理解的话我们进行一次手推,使用heapinsert将数组{5,3,6,7,7}整理成为一个大根堆,图如下:
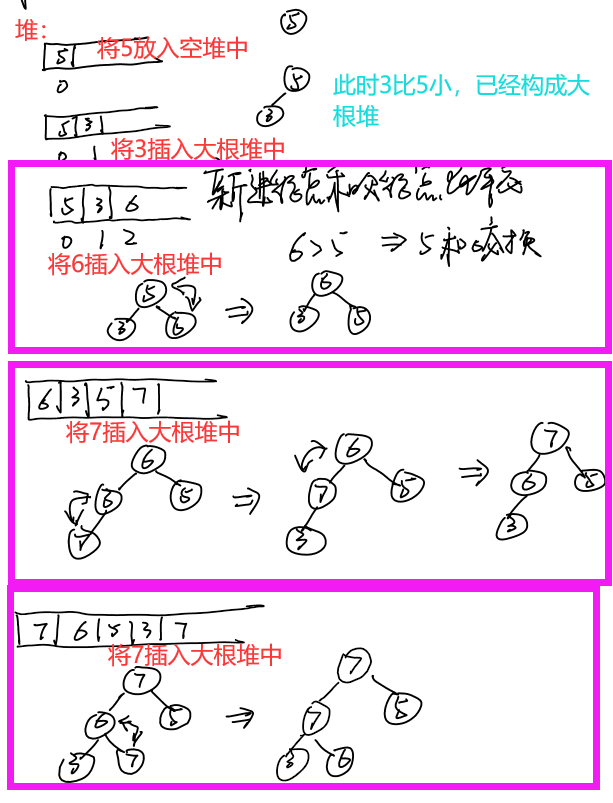
伪代码如下:
void heap(int *a,int n){
int heapsize = 0;
for(;heapsize<n;heapsize++){
heapinsert(a,heapsize); //让每个数组元素进行heapinsert插入大根堆中进行整理
}
}
三、heapify函数
1. 手推一轮heapify
如果说heapinsert是自下向上整理数组元素为一个大根堆/小根堆的话,那么heapify就是自上向下整理数组元素成为一个大根堆/小根堆。
heapify:在一个大根堆中,要求返回堆中最大值,并要求去掉堆中最大值。
基本思路:将堆中(共有heapsize个元素)堆尾元素与堆顶交换,返回堆顶元素,将剩余元素(
heapsize = heapsize-1)个元素整理为一个大根堆。比较该堆尾元素与目前所处的位置的左右孩子中最大值的大小,若该元素比其小,则与其中一个子节点做交换,继续进行比较,直至该元素大于它的子节点,则该堆重新整理好了。
图解如下:
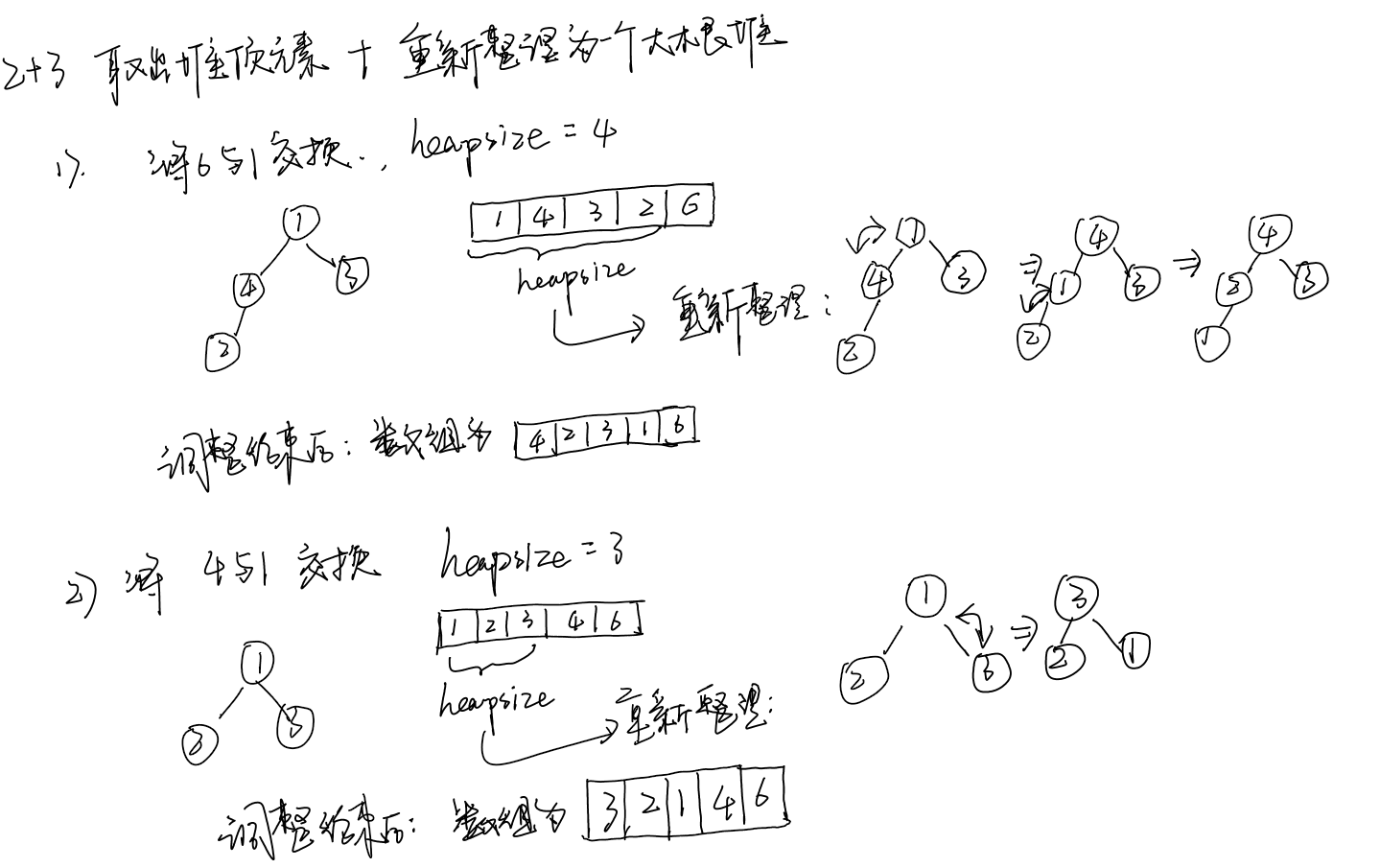
大根堆{6,3,5,2,3,4},此时heapsize = 6,返回最大值,并将其余元素重新整理为一个大根堆。

代码如下:
void heapify(int *a,int *heapsize){
//这里需要注意,heapsize是堆中数目的个数,但不是堆中最后一个元素的下标
//堆中最后一个元素下标为*heapsize-1
while( (*heapsize)>0 ){
swap(&a[0],&a[(*heapsize)-1]); //交换堆中的根节点和最后一个子节点
(*heapsize)--;
//整理heapsize的部分重新构成大根堆
int i = 0;
while( (i*2+1)<=( *heapsize-1) ){ //判断是否有子节点
if((i*2+2)<= *heapsize-1 ) //左右孩子都有
{
int temp = (a[i*2+1]>a[i*2+2])?i*2+1:i*2+2;
if(a[i] < a[temp]){ //右孩子是否存在 ,找两者其中较大的一个
swap(&a[i],&a[temp]);
i = temp;
}
else{
break;
}
}
else{ //只有左孩子
if(a[i] < a[i*2+1]){ //没有右孩子的情况下,直接和左孩子进行比较
swap(&a[i],&a[i*2+1]);
i = i*2+1;
}
else //如果没有出现交换操作,说明已经到达了合适位置
break;
}
}
}
}
2. 使用heapify整理数组成为一个大根堆
我们知道heapify是自上至下将一个新元素整理进一个大跟堆,那么我们就可以从数组的最后一个元素(堆的最右下元素)开始,每个元素进行heapify,将其整理为一个大根堆。
void heap_sort(int *a,int n){
int i = n;
for(;i>=0;i--){
heapify(a,i); //从最后一个元素开始调整一个大根堆
}
}
四、heapinsert和heapify形成大根堆的时间复杂度
我们上述的两个函数都是被调整元素与其父节点或者子节点中最大值作比较,都是只与该堆的高度(该完全二叉树的高度)有关,当堆中元素为N个时,则该堆高度为logN,也就是说每进行一次heapinsert或者heapify的时间复杂度为O(logN)。
那么分别使用这两者构成一个堆的时间复杂度是多少呢,heapinsert很显然为O(NlogN),但是heapify就有些特殊了,当一个数组中的元素全部给出我们用heapify从最右下元素开始调整,由于最后一行元素(当一个堆的元素为N时,最后一行的元素几乎有N/2个)都不会有交换操作,所以会大大提升效率,最终的时间复杂度为O(N)。证明如下:

五、手推堆排序
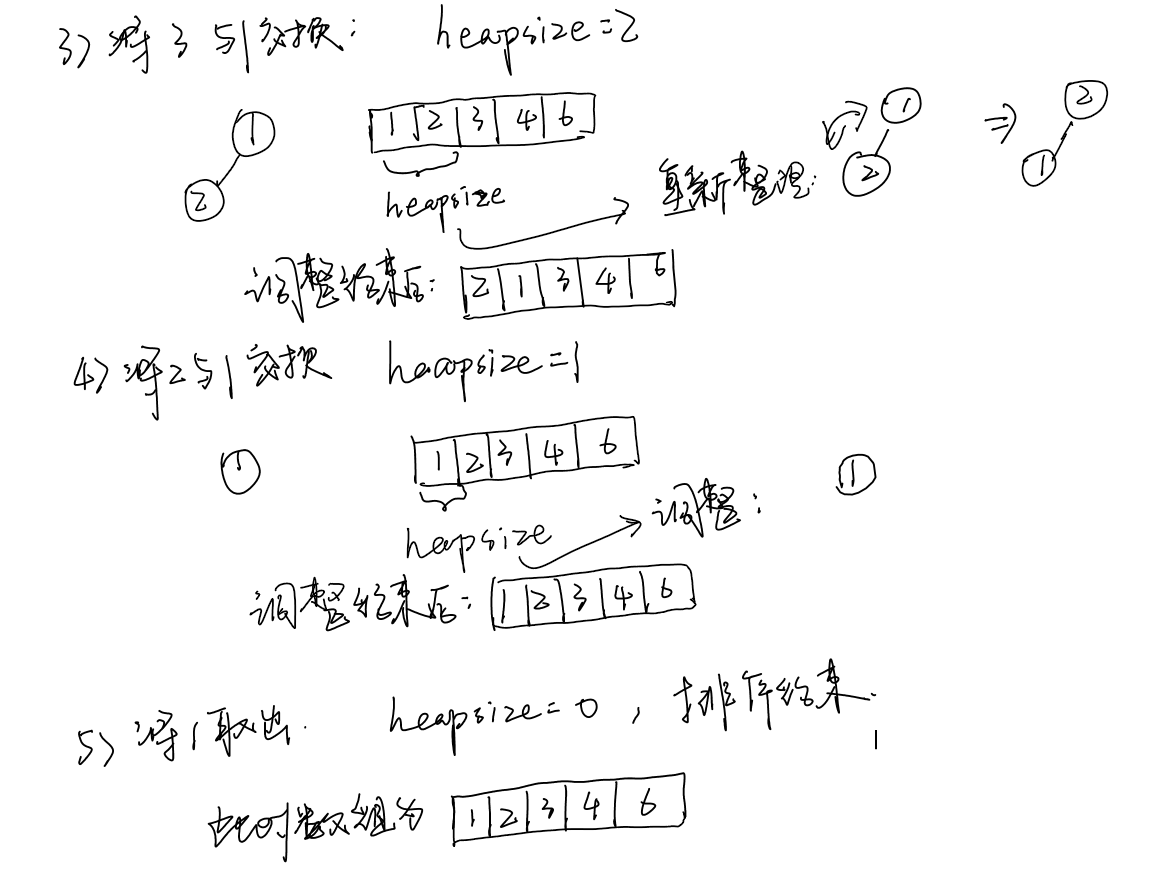
终于到了我们的堆排序了。在以下排序过程中我们以大根堆为例:
基本思路:
- 首先将数组中所有元素整理为一个大小为heapsize的大根堆
- 取出堆顶元素,将其与堆尾元素做交换,
heapsize--;- 将大小为heapsize的新堆使用heapify整理为一个大根堆
- 循环2,3,直至heapsize = 0,此时数组中的元素自小到大有序。
如图手推堆排序:

六、堆排序代码
#include <stdio.h>
void heap_sort(int *a,int n);
void heapinsert(int *a,int heapsize);
void heapify(int *a,int *heapsize);
void swap(int *a,int *b);
void heap_sort(int *a,int n){
int heapsize = 0;
for(;heapsize<n;heapsize++){
heapinsert(a,heapsize);
}//形成一个大根堆
heapify(a,&heapsize);
}
void heapinsert(int *a,int heapsize){
int i = heapsize;
while(a[i] > a[(i-1)/2]){
swap(&a[i],&a[(i-1)/2]);
i = (i-1)/2;
}
}
void heapify(int *a,int *heapsize){
//这里需要注意,heapsize是堆中数目的个数,但不是堆中最后一个元素的下标
//堆中最后一个元素下标为*heapsize-1
while( (*heapsize)>0 ){
swap(&a[0],&a[(*heapsize)-1]); //交换堆中的根节点和最后一个子节点
(*heapsize)--;
//整理heapsize的部分重新构成大根堆
int i = 0;
while( (i*2+1)<=( *heapsize-1) ){ //判断是否有子节点
if((i*2+2)<= *heapsize-1 ) //左右孩子都有
{
int temp = (a[i*2+1]>a[i*2+2])?i*2+1:i*2+2;
if(a[i] < a[temp]){ //右孩子是否存在 ,找两者其中较大的一个
swap(&a[i],&a[temp]);
i = temp;
}
else{
break;
}
}
else{ //只有左孩子
if(a[i] < a[i*2+1]){ //没有右孩子的情况下,直接和左孩子进行比较
swap(&a[i],&a[i*2+1]);
i = i*2+1;
}
else //如果没有出现交换操作,说明已经到达了合适位置
break;
}
}
}
}
void swap(int *a,int *b){
int temp;
temp = *a;
*a = *b;
*b = temp;
}
int main(){
int n;
printf("请输入数组长度:");
scanf("%d",&n);
int a[n];
printf("请输入您想要进行排序的数:n");
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
}
heap_sort(a,n);
for(int i=0;i<n;i++){
printf("%d ",a[i]);
}
printf("n");
}
好了这就是我们的堆排序内容了,希望大家读完之后能有所收获。
最后
以上就是过时鼠标最近收集整理的关于堆排序图文详解一、什么是堆?二、 heapinsert函数三、heapify函数四、heapinsert和heapify形成大根堆的时间复杂度五、手推堆排序六、堆排序代码的全部内容,更多相关堆排序图文详解一、什么是堆?二、内容请搜索靠谱客的其他文章。








发表评论 取消回复