
这个堆,跟栈堆是不一样的,但要用的单词是一样的
堆是一个完全二叉树(除了最下一层是叶子,上面应该都是满的,最下面一层紧左边放才是完全二叉树)
堆有大顶堆,小顶堆
每个非叶子结点都要大于或等于其左右孩子结点的值称为大顶堆
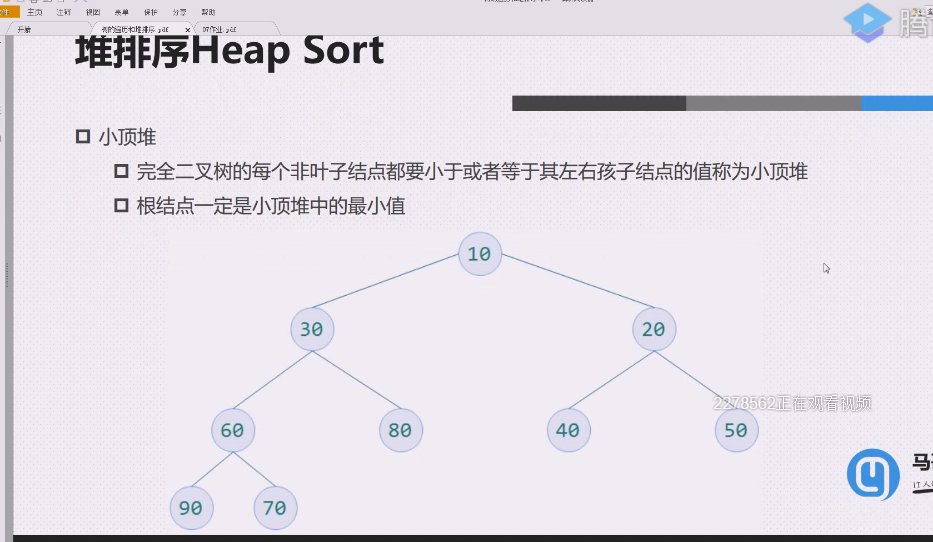
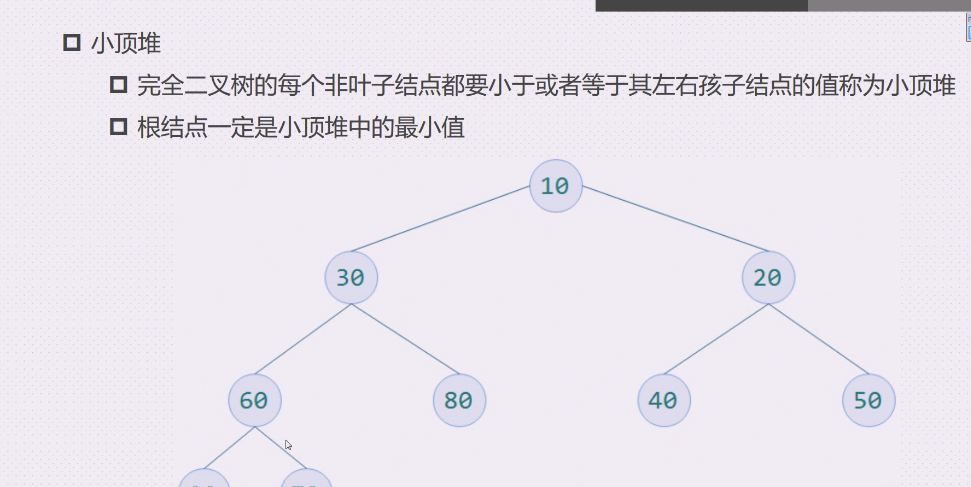
每个非叶子结点都要小于或者等于左右孩子结点的值称为小顶堆
根结点一定是大顶堆中的最大值,一定是小顶堆中的最小值
大顶堆,要求左子树和右子树的值不大于上面的跟结点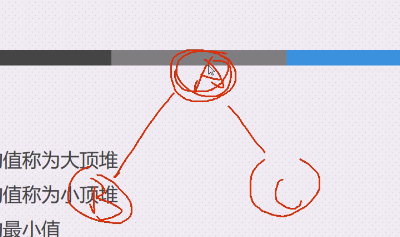
小顶堆,A这个根节点的值,是里面最小的
大顶堆则是三个值里面最大的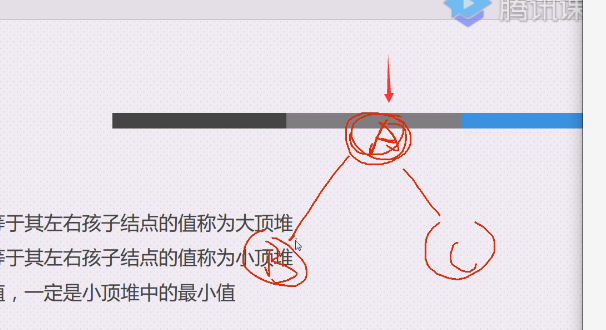
大顶堆就是,A在ABC里是最大的,B在BDE里是最大的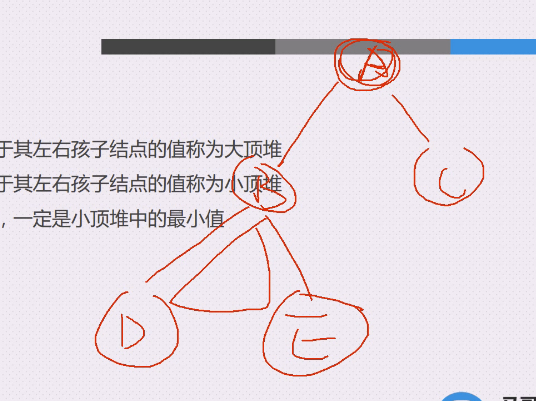
如果构建的是大顶堆,这个堆顶一定是整个数组里最大的

如果是小顶堆,这个堆顶应该是整个数组的最小值
大顶堆
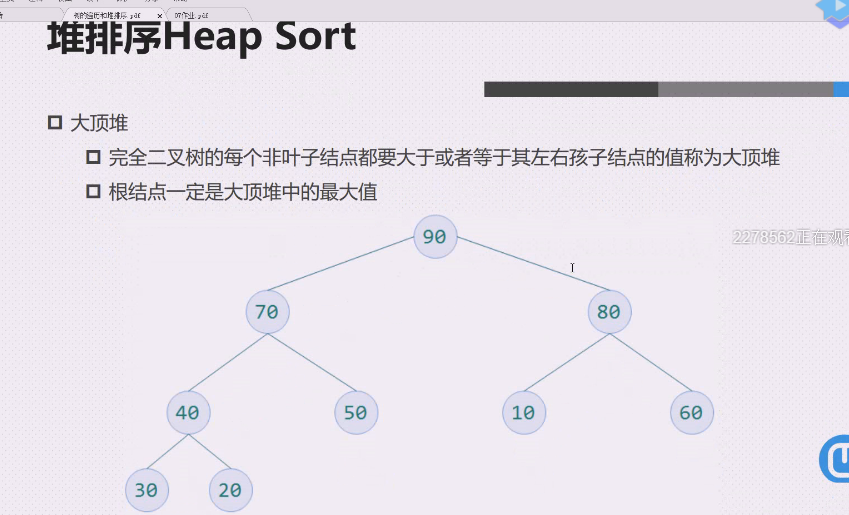
大顶堆:
完全二叉树的每个非叶子结点都要大于或者等于其左右孩子结点的值称为大顶堆
根结点一定是大顶堆中的最大值
小顶堆
要求这个结点和左右孩子结点,都应该有个约束
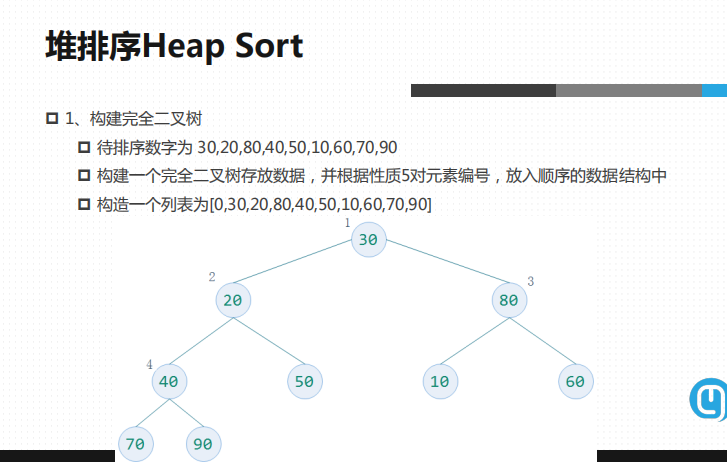

堆排序首先要构建一个完全二叉树
待排序数字为30,20,80,40,50,10,60,70,90
构建一个完全二叉树存放数,并根据性质5对元素编号,放入顺序的数据结构中
构建一个列表为[0,30,20,80,40,50,10,60,70,90]
如果i的编号是按层来编,就存在2i和2i+1的问题
i的左孩子结点是2i,右孩子结点是2i+1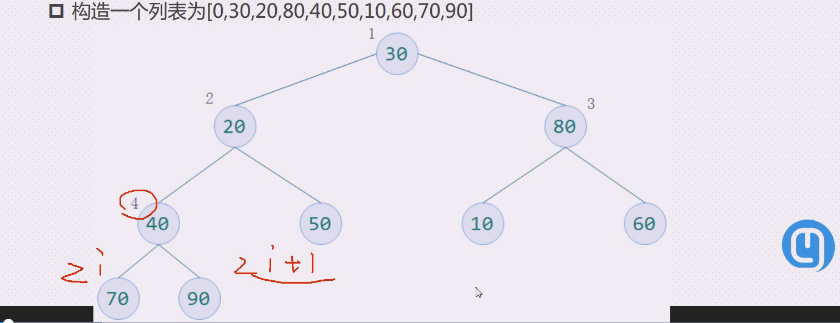
如果2i>当前结点树,则结点i无左孩子,即结点i为叶子结点;否则其孩子结点存在编号为2i
比如1+2+4=7 n=7
2i =8>7,就没有左孩子结点
还有2 i+1>n,只能说明没有右孩子结点,不能说明有没有左孩子结点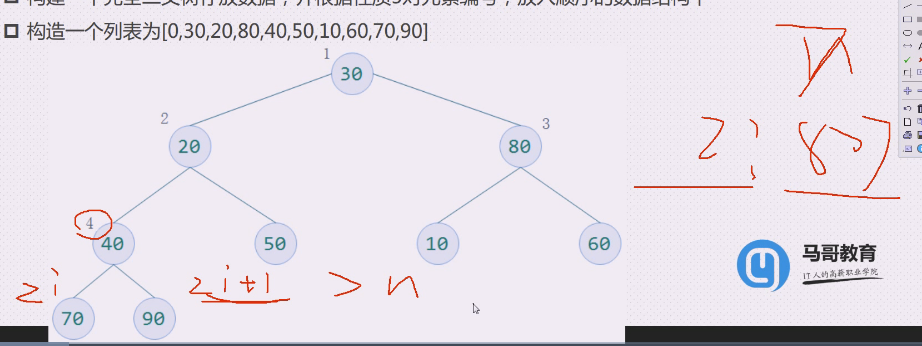
为什么i从1 开始,我们在列表补0就是为了这个,只要你现在有i就可以判断这个树,有没有左孩子右孩子

索引是2,22=4,22+1=5,能对应起来,变成了一个序列,这就是层序遍历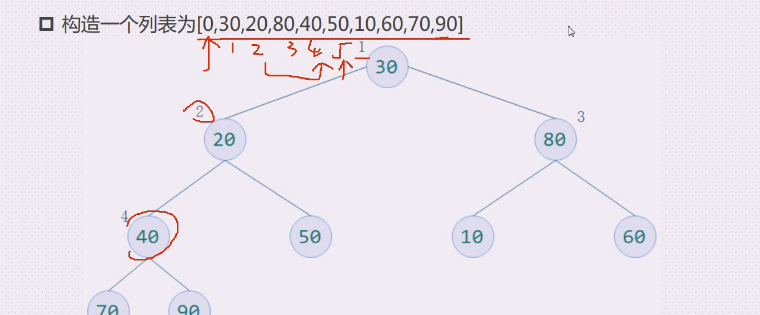
这就是完全二叉树,为了用大顶堆和小顶堆进行排序,
第一步,将二叉树性质5对应起来的东西,在列表前面凑0就出来了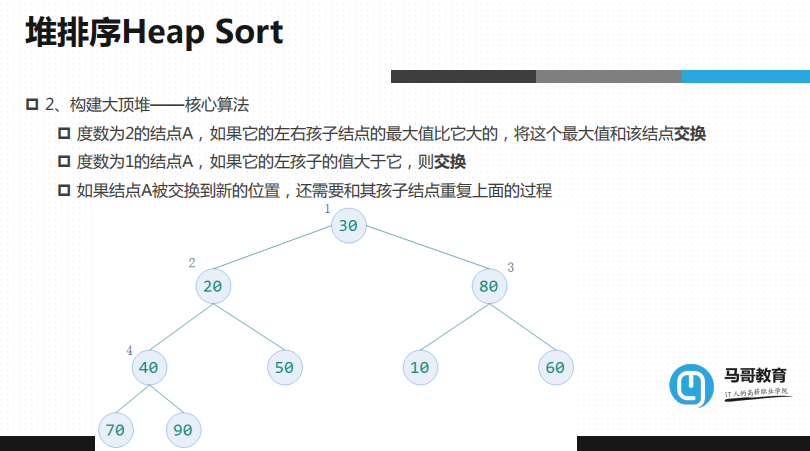
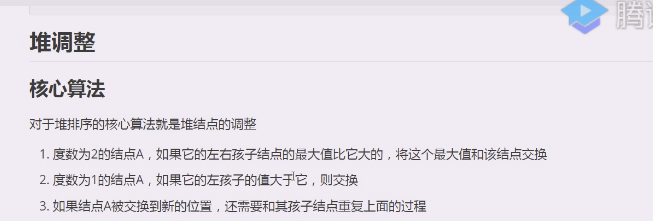
虽然满足了完全二叉树但是不一定满足大顶堆,需要做调整,让他作为一个大顶堆,核心算法:
度数为2 的结点A,如果它的左右孩子结点的最大会比它大的,将这个最大值和该结点交换
度数为1的结点A,如果它的左孩子的值大于它,则交换(完全二叉树,度数为1就不可能有右孩子结点)
如果结点A被交换到新的位置,还需要和其孩子结点重复上面的过程
三个比较就是,90上去,40下来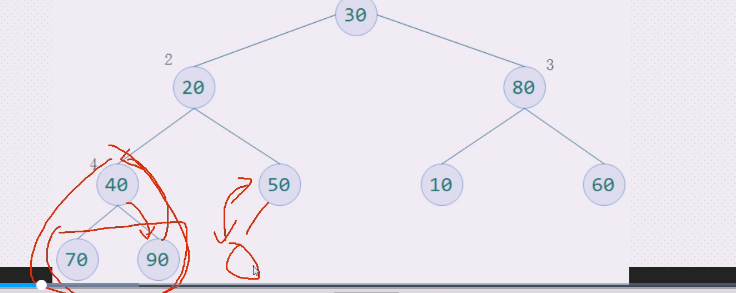
左下三角就是90和40
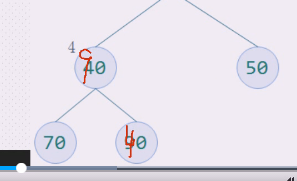
都需要调整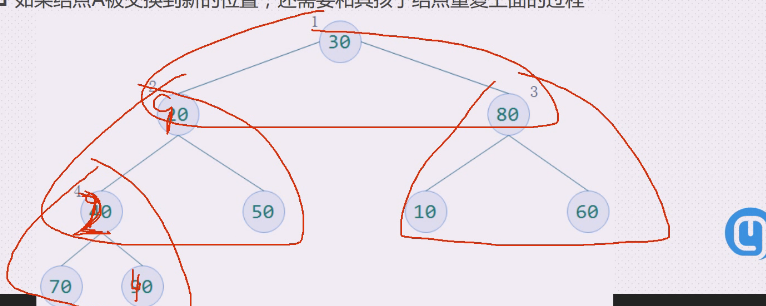
**第一个,先80和30互换
右边的三角 **
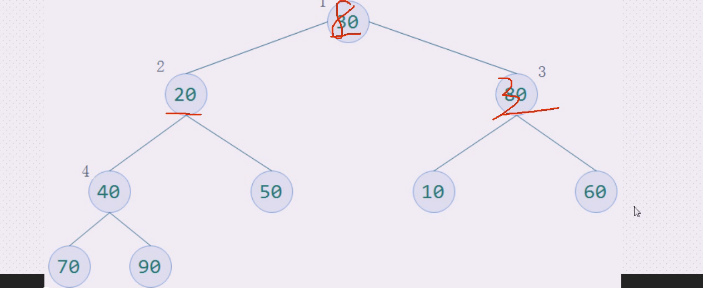
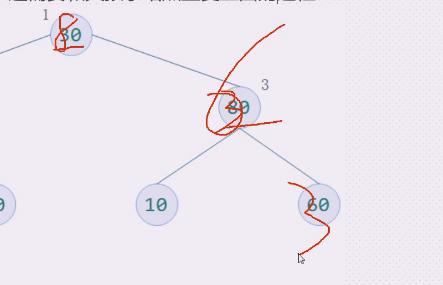
右边的60上,30下
查看2这边如何操作,20,40,50,
50上,20下,停止
但是这样就不好调整大顶堆,需要一个顺序
应该是4到3,3到2,2到1 ,倒着走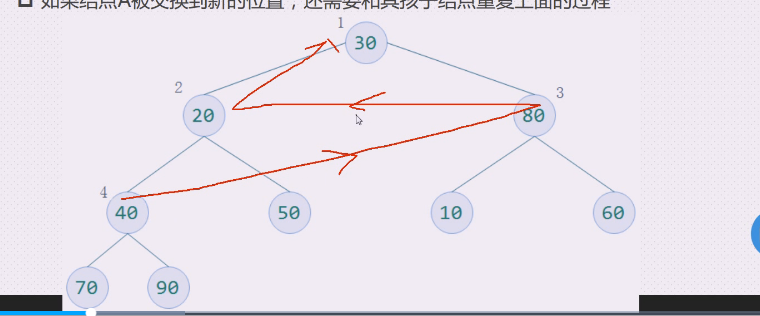
构建大顶堆,起点选什么很重要
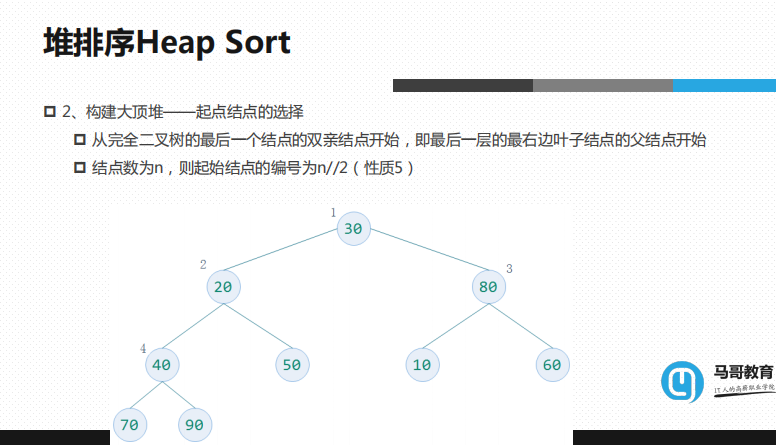
从完全二叉树的最后一个结点的双亲结点开始,即最后一层的最右边叶子结点的父结点开始
结点数为n,则其实结点的编号为n//2(性质5)
最后的叶子结点是9,
9//2=4
就是2i+1 =8+1=9 //2 =4
起点就从最后一个最右侧结点开始,从它的双亲父结点开始,由它4321这么来找
起点是从最后一个结点的父结点开始,下一个节点选择就是4321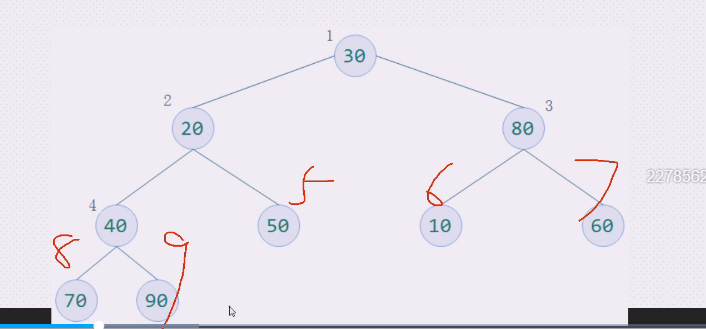
大顶堆的目标就是现在这个样子,但是有可能调整完数字可能不一样
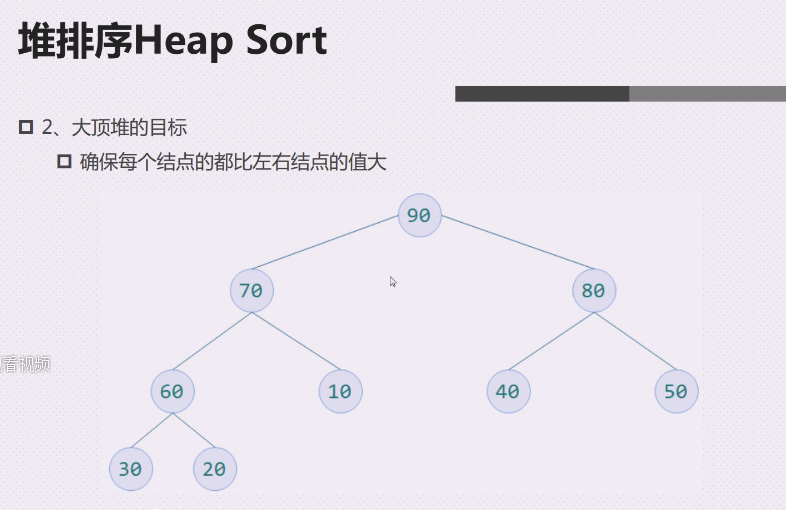
目标:
确保每隔结点的都比左右结点的值大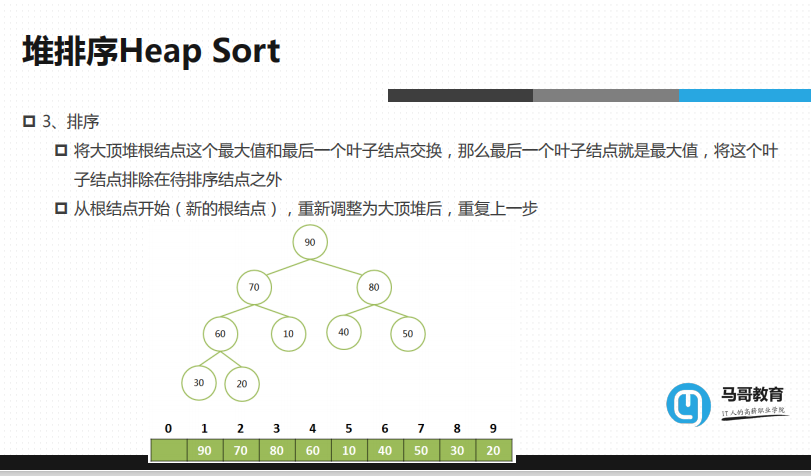
最后是个排序的过程,大顶堆在内存中怎么画的,就是上面的列表,跟列表的索引对应关系就是这么放的,当你拿到大顶堆,下面就要开始排序了
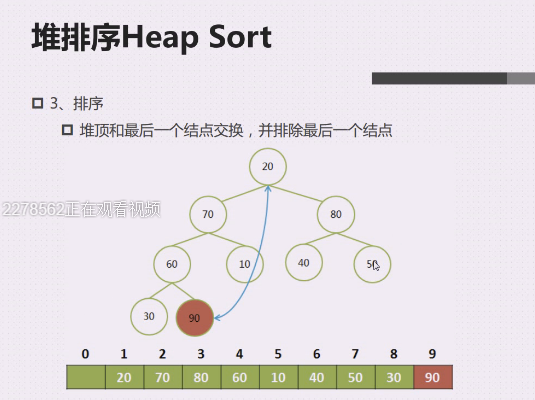
从根节点开始,将大顶堆的根节点的这个最大值和最后一个叶子结点交换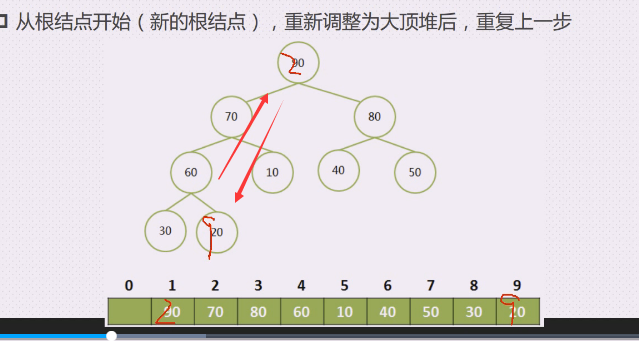
90跟20交换,现在就不是大顶堆了
90就是有序区,其他的都是无序区
由于20的加入,引起了整个堆的不平衡
从20开始就要向下调整
20,70,80,谁最大 80最大,上调,20就到了右边,20,40,50,50最大,50上调
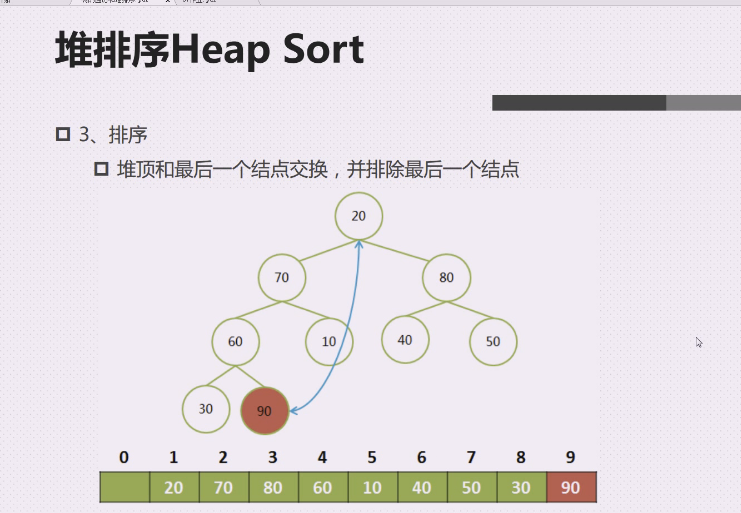
由于20的加入,引起了整个堆的不平衡
从20开始就要向下调整
20,70,80,谁最大 80最大,上调,20就到了右边,20,40,50,50最大,50上调,20下不去了,就到此停止,
20完了,说明大顶堆在排序过程到这一阶段已经完成了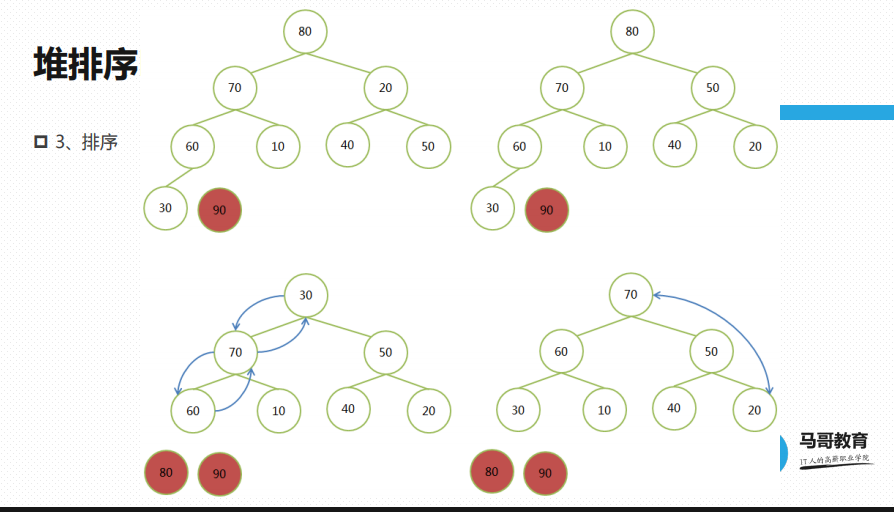
现在堆顶是80,80是最大值,80拽下来,30上去
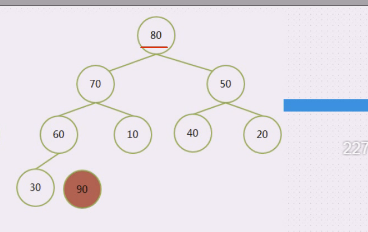 80拽下来,30上去,30在堆顶,把30和70进行交换,30下来,70上去,底下有60和10,60上,30下
80拽下来,30上去,30在堆顶,把30和70进行交换,30下来,70上去,底下有60和10,60上,30下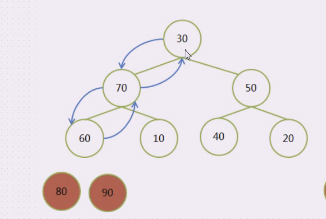
就变成了70,60,30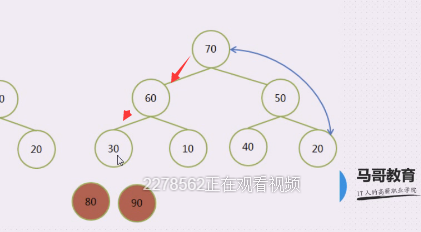
这样的算法是,在堆顶上引入不规定数据,制造混乱,就堆顶向下调,一路向下,一直到调完为止
现在是70,70要跟20做对调,20上,70下,
70固定下来,20就走60,60上,20下 30上,20下
70固定下来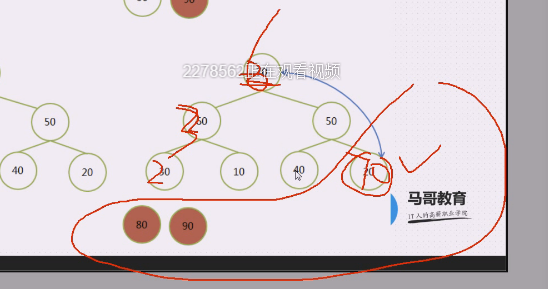
然后60跟40,40上,60下,也固定下来了,40上了,和50比,50上,40下,右边就走不下去了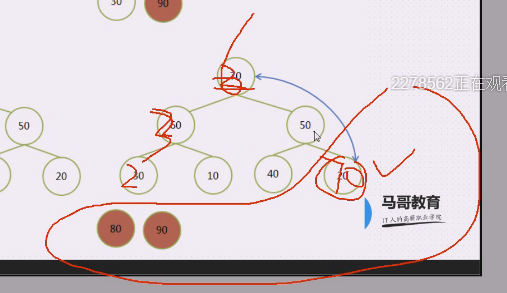
这样在堆顶就一直在拿一个东西,要么是最大值要么是最小值,从顶上一直在拿一个当前的最大值,然后和当前的元素交换,从线性结构来看,就是最右边就是不停固定,有序区越来越大,无序区越来越小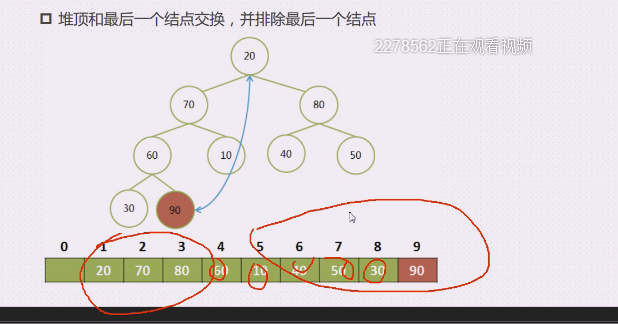
我们在内存中其实玩的是一个列表,是没有树的
算法实现
核心算法就是一个结点与它的左右子树进行比较,然后把极大值和极小值放在这个位置上,总之要进行调整,在调整中,某一个值往下去了,要在下面的新位置上,在下面的左右子树节点再进行比较,直到真正的不能动为止,
第一个阶段是要构建一个大顶堆,等你堆顶上有了一个极值,才能在堆顶上拿走一个,放一个小数上去,打破原来所谓的大顶堆,然后让它重新调整
但是第一个大顶堆从哪里来,从下面这个算法来
大顶堆的调整

为了索引算起来好办,就添一个0,索引从1 开始,就跟性质5的编号123456的一致,
代排序数就是这个长度减一total=len(origin)-1

下面就是堆调整,要调成大顶堆,大树在上,小数在下
首先给n个数,给n个数,当前i是几
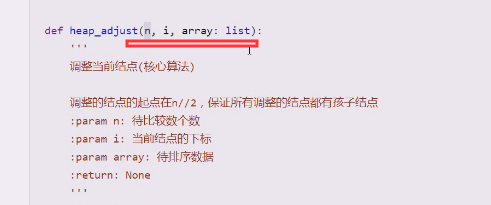
print_tree按照道理不是在堆排序中的,纯粹打印起来是看着空间结构的,如果从线性结构去理解这个算法,会绕晕的
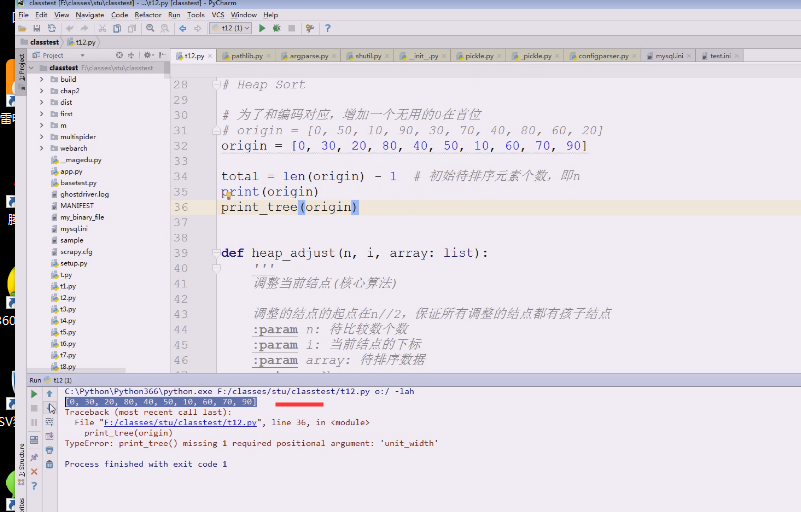
改成2,打印试试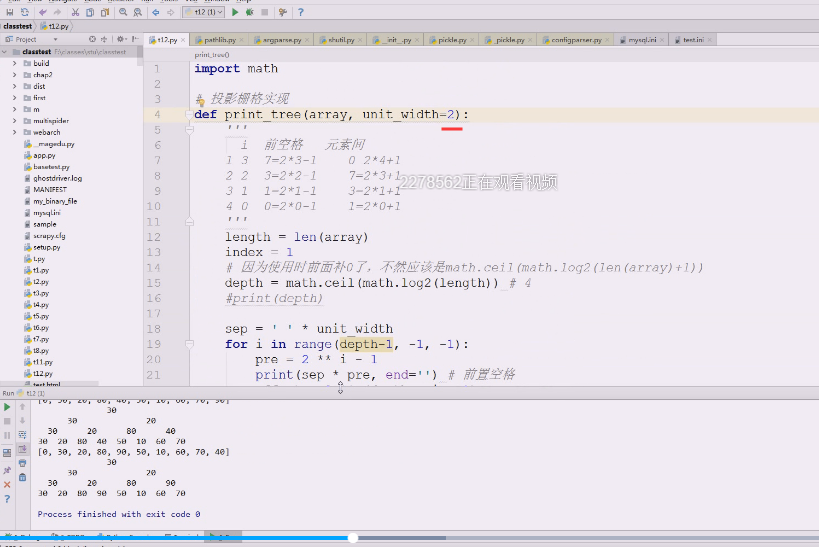
index要加一下,不加的话每次从1 开始是不行的,用完多少便宜多少
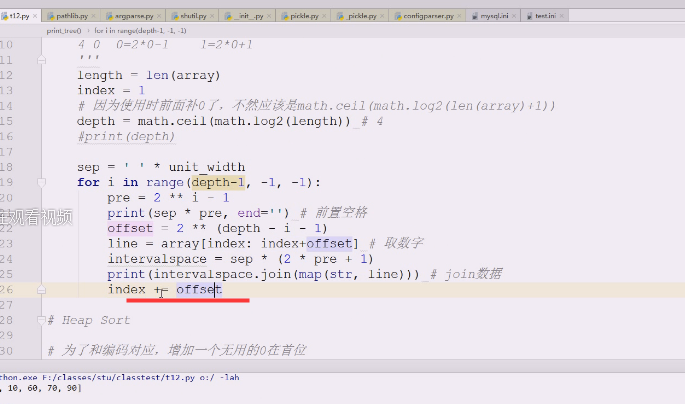
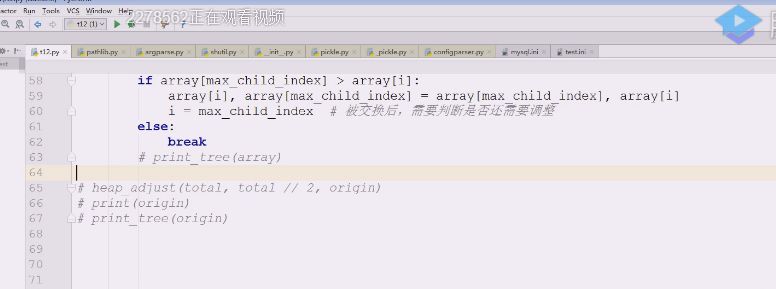 这个序列打印之后是这个样子
这个序列打印之后是这个样子
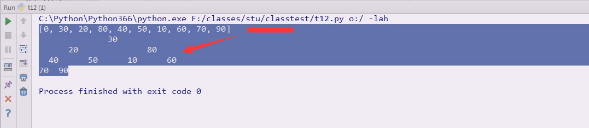
现在要构建大顶堆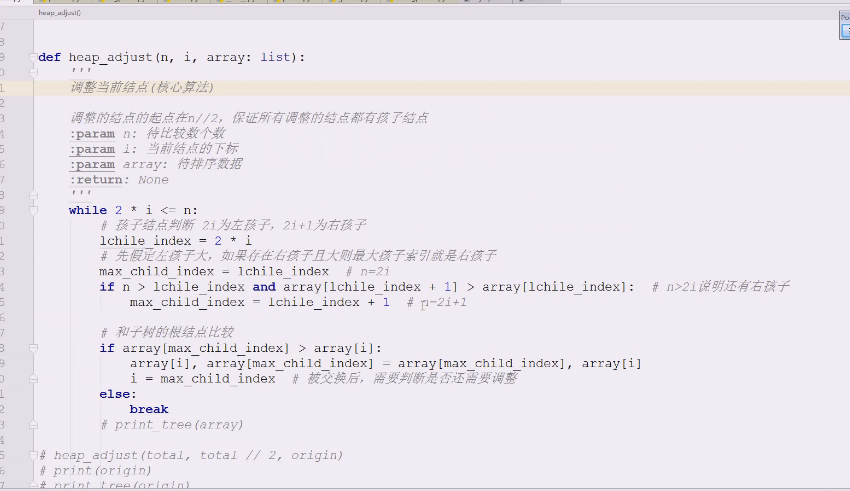
首先几个数比较要说明
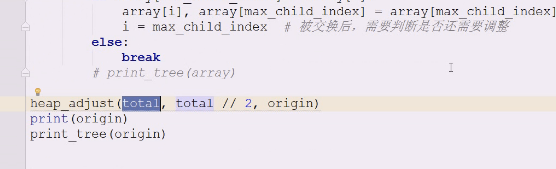
长度减一个数做比较

这个数放进来正好是total//2的取整,

待比较数就是9个,9整除2才对=4
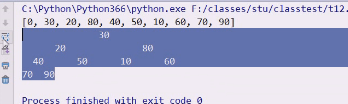
4就是刚好40,按照性质5编的号,从4开始调整,orign就是原始的序列
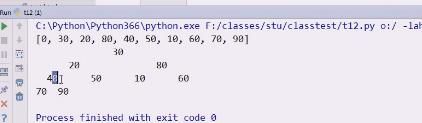
先解决左孩子的问题,左孩子就是2i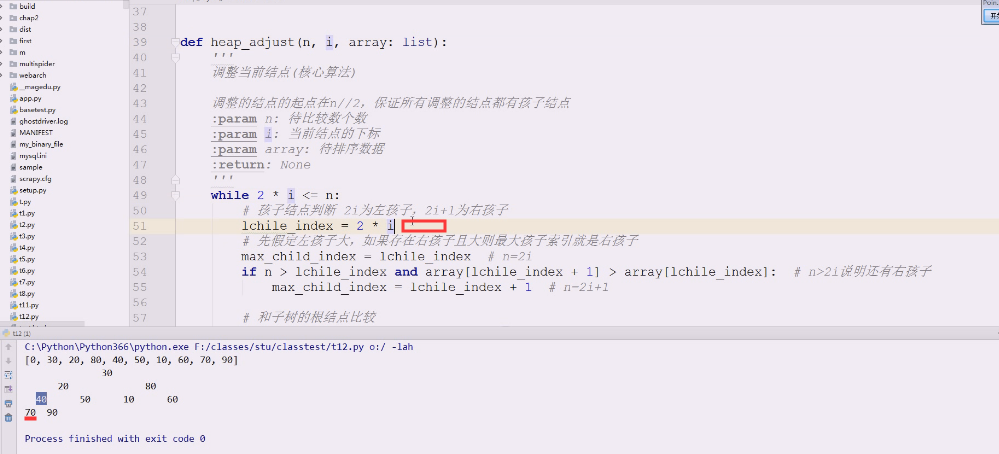
左孩子的索引堪称最大值的索引,先这么假定
如果n>左孩子结点,说明一定有右孩子,则右孩子结点=2i(左孩子le_index)+1
如果有右孩子,且 右孩子结点的值大于左孩子结点的值
孩子结点的最大值索引就等于右孩子结点的索引
假定左孩子一定有,因为total//2 除进来就表示一定有,
这就是在左右孩子中找到一个最大值
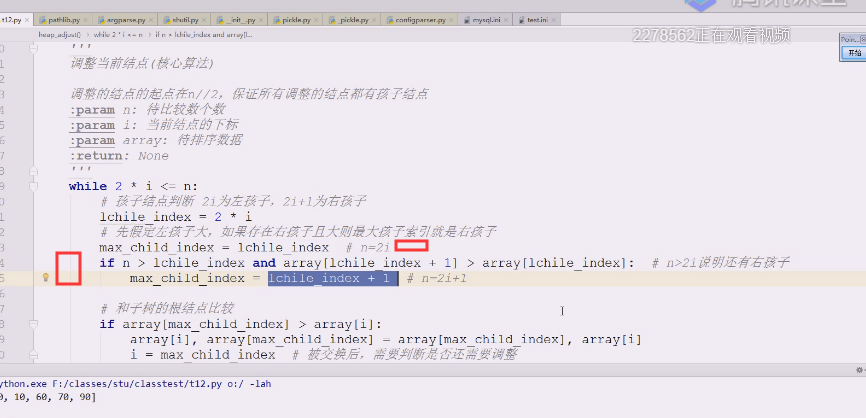
这几个最大值就要跟当前结点比,当前结点是array[i],左右孩子中,最大值的索引,与父结点的值进行对比,
if array[max_child_index] >array[i]:
如果这个大于
要把最大孩子索引赋给I i =max_child_index,原来最大孩子是9,i是4,9跟4调换完以后,把i改成9,因为大数往上去了,小数沉下来了,如果再有左右孩子,就不符合大顶堆的要求
这时候如果9下面还有左右孩子,就需要让9继续对比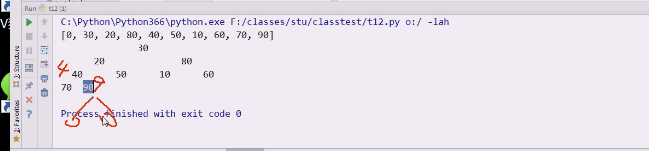
**所以现在相当于把9赋给i,i从原来的4变成9,就是换了个索引,9得到了i,所以如果9下面还有左右孩子结点就需要继续比较,所以这里回头了
**
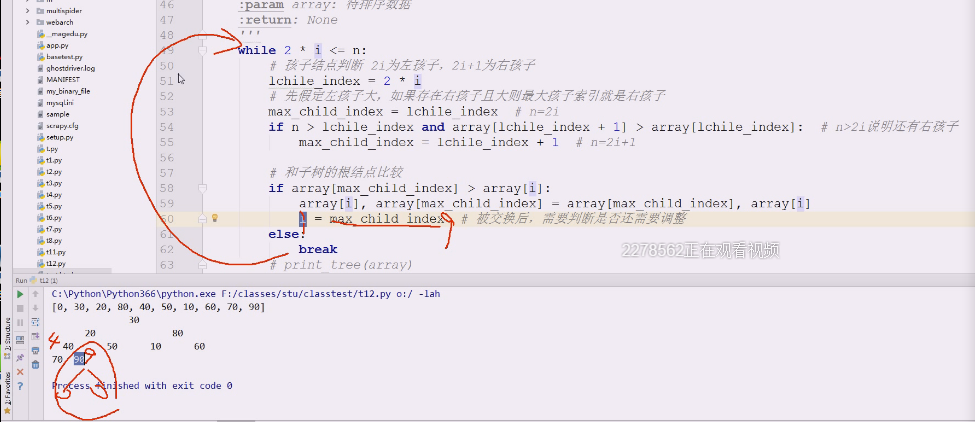 回头不要紧,首先要判断下,有没有孩子结点,这个就判断有没有孩子结点
回头不要紧,首先要判断下,有没有孩子结点,这个就判断有没有孩子结点
性质5
如果2i=n,恰好有左孩子结点,但是现在i是9,2*9=18.没有这么大的编号,就不进去了
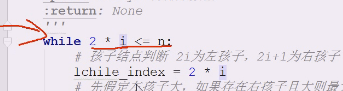
这个单个结点的调整过程
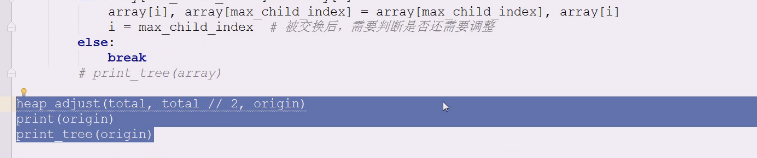
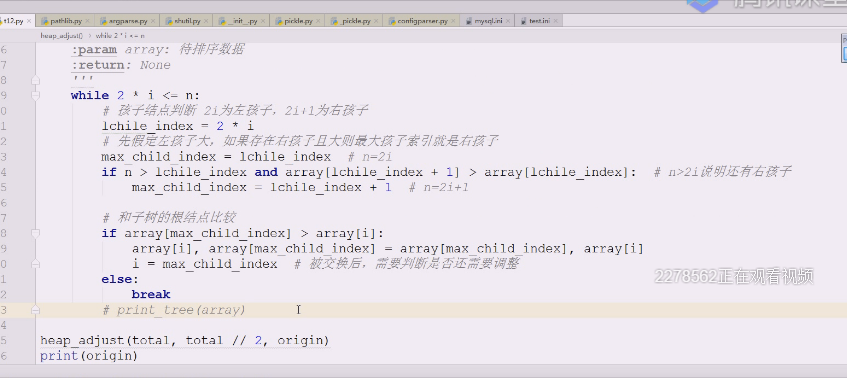
再挑一个数字代入试试,30,i=1 ,n=9
左孩子结点 2*i=2
假定左孩子结点最大,通过观察,右孩子结点有
左右孩子比较除,谁大谁小,这个时候明显最大的就是3 i=3,80
这时候3跟1比,3是80,1是30
80上,30下
i现在是等于3的情况
右边的就是30,10,60
30现在对应的i是3, 10对应6,60对应7
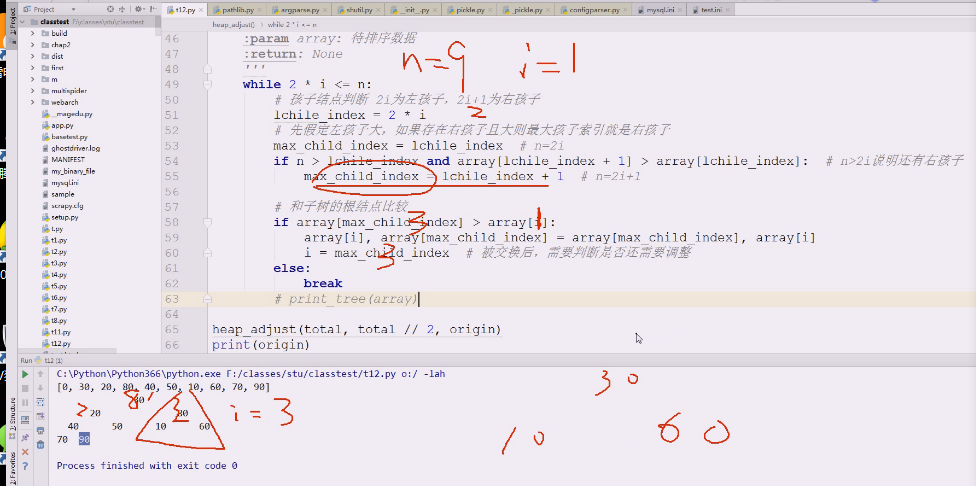
现在回头,i=3,2i =6 <=9进入循环,
假定左还是最大 lchile_index =2i=6
问左右孩子谁大,这时候就是 7
7跟 3比,7的索引值大,他们就交换,上面变60,下面变30
i跟着30走,i=7
再回头 2*7=14超出n了,就不进入循环了,只要从上往下走,下来就跟着,然后看下面的左右子树是不是构成大顶堆,不能构成就再调整,再调整就又下去了,遇到左右子树就再调整
从上往下调,到下面再看这个左右子树
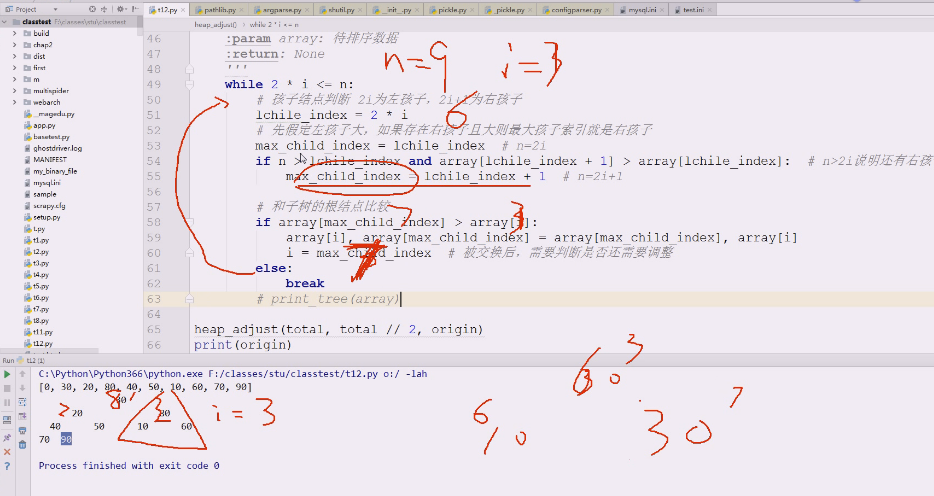
只有小的往下走,大的才能往上冒
这个函数是单个结点调整
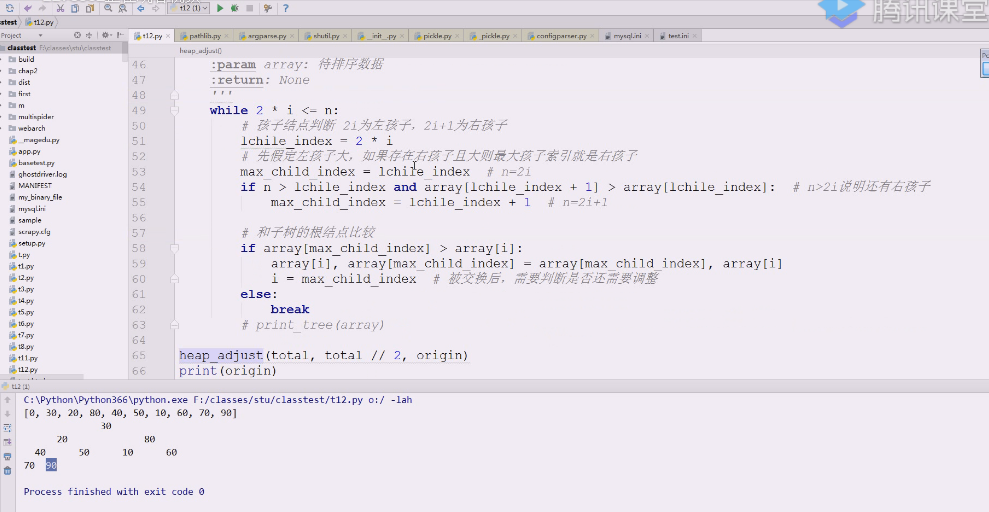

构建大顶堆

第一个整数就是4,从这里开始走,4321
i是一直在变 (total,i,array)
调整完return array就可以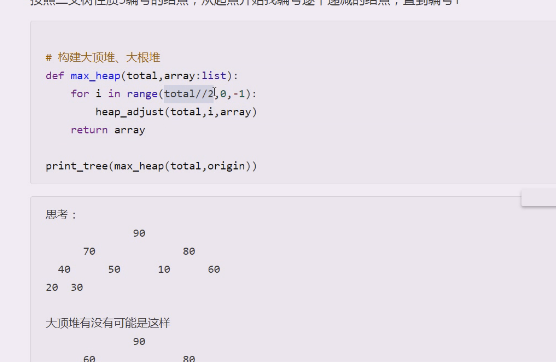
就调整成了大顶堆
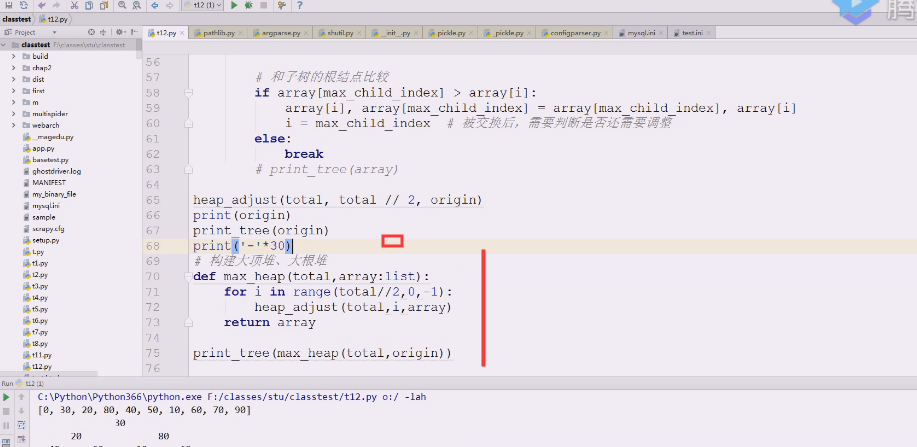
正好满足大顶堆,选择从最后一个结点的父结点开始,倒着走,编号更小的走一下,直到编号1为止,
现在是4321,正好调整4下
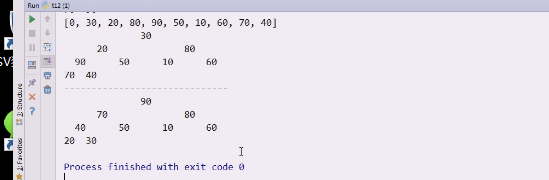
现在有了大顶堆就可以排序了
查看每一次调整的过程
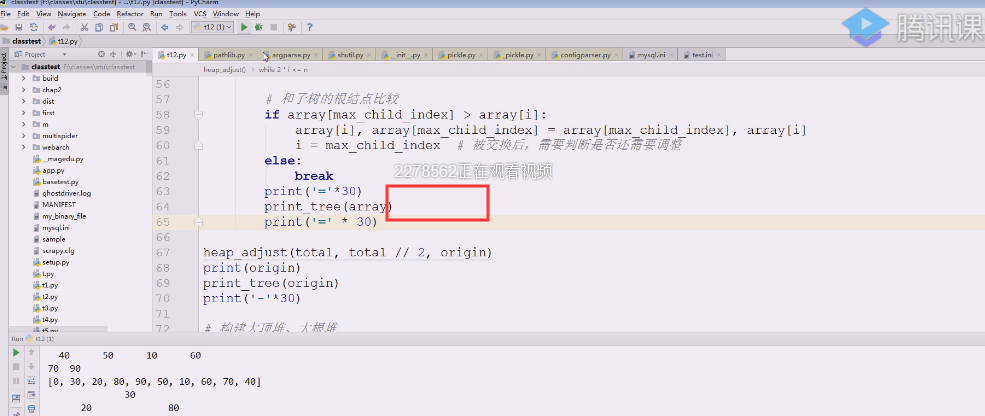
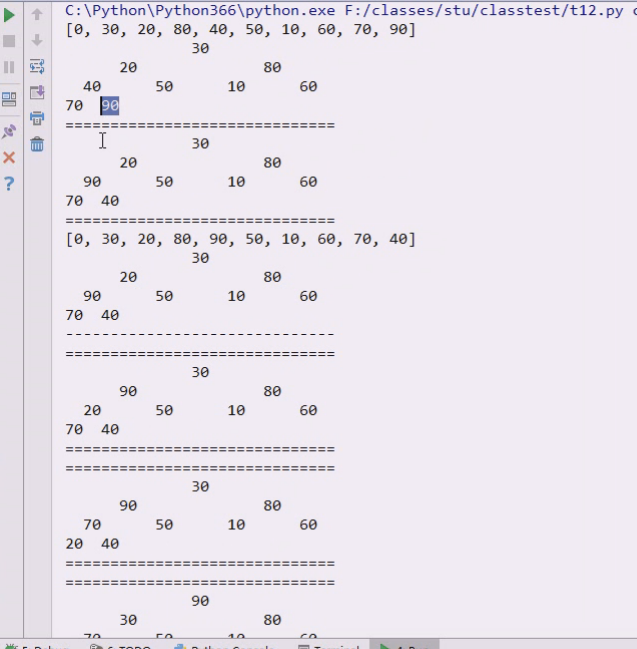
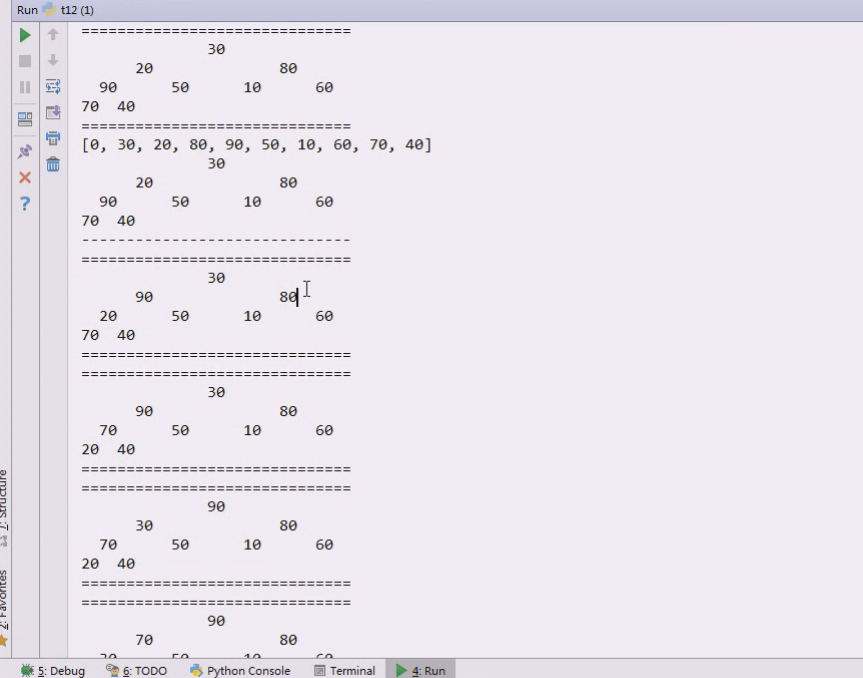


90上来,40下去了

90又动了,挪上去,20下来,20跟70就要准备挪一下
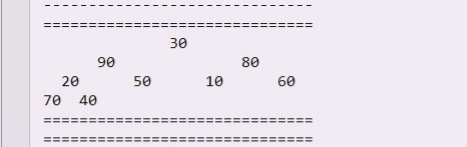
20跟70挪一下,70上,20下,最后90和30,80比较
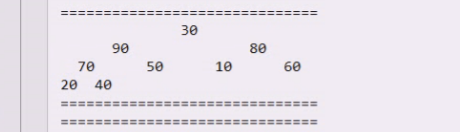
90上,30下
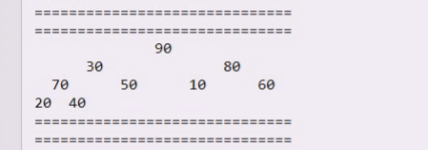
30听不了,70上,30下

40上30下

最后90,80,70不用动

剩下的就是排序了
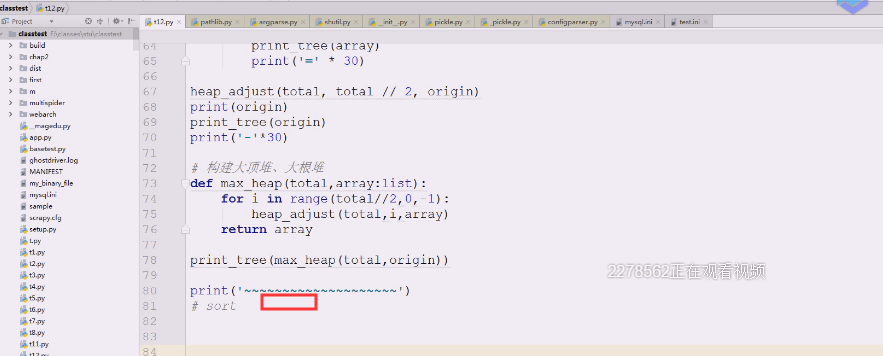
按照刚才的大顶堆排序方式,从顶上消下去即可,把最下面的拿上来
30上90下,30往80跑,80上30下
30,60,10 60上30下

下一步要做的事情就是要一个个去拿


为了得到最后,90.80,70这样一个排序,升序降序,有可能构建的大顶堆可能不一样,但是构建的大顶堆不一样,但是可能满足大顶堆的定义
总结,最大的一定在第一层,第二层第一有一个次大的,一个大顶堆,最大值在顶上,次大的一定在第二层
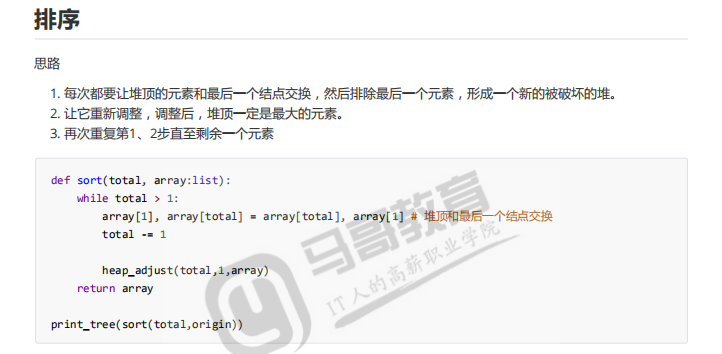
排序思路:
1.每次都要让堆顶的元素和最后一个结点交换,然后排除最后一个元素,形成一个新的被破坏的堆。
2.让它重新调整,调整后,堆顶一定是最大的元素。(小数往下跑,一定会引起大顶堆的变化,这个小数就会被迫进行调整,次大值就一定会出来)
3.再次重复第1、2步直至剩余一个元素
总在破坏大顶堆,总在构建大顶堆,每一次都在当前的无序区,选择一个极大值或者极小值,所以这种叫选择排序
堆排序是一种选择排序,因为每一次的调整过程都是从当前的数列中去找出最大值最小值
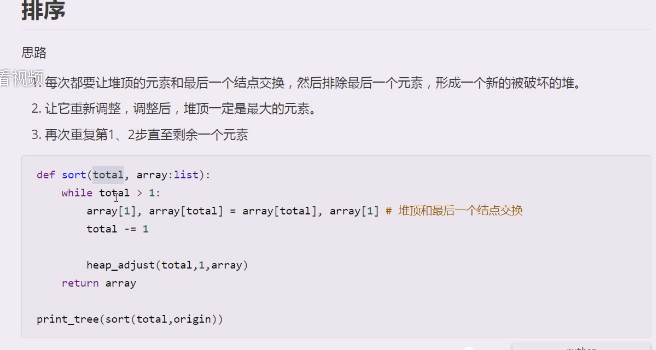
给,一个总数,如果这个数是大于1的 
total是堆顶,9,每次-1,在堆尾,你要交换的数每次都在减1,总之要明白,已经固定下来的数,不要参与
堆顶一定是在索引为1的地方,索引为1 的覅那个和跟当前无序区的最后一个交换一下即可
交换之后,堆就被破坏掉了
(构建大顶堆,是4321,拿到大顶堆之后开始破坏大顶堆,堆顶和最后一个元素做交换,堆顶变了,索引为1就变了,所以就从1开始,继续去调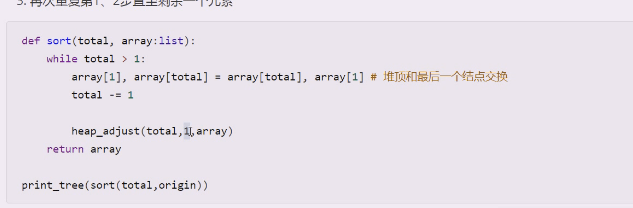
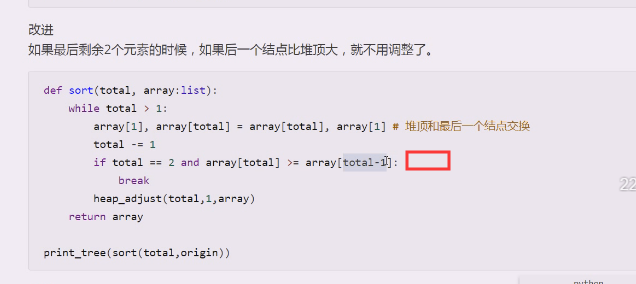
改进
如果后一个结点比堆顶大,就不用调整了,因为现在是升序,左孩子结点比它大,剩下的2个 结点只是它自己和左孩子,就不用调整了
就是索引2>索引1,根本就不用动了
堆排序想在某一趟提前结束还真的不能,也就只能在特例的地方加一些判断了
先看完成代码


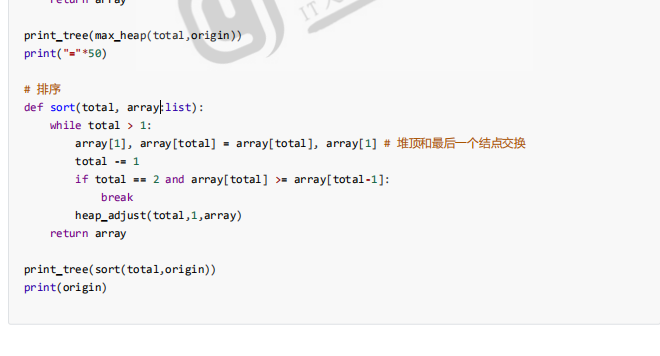
这个排序算法就是首先构建一个二叉树,只能用列表来构建这个二叉树,该怎么描述,所以最好的描述方法就是性质5,性质5 的描述是从1开始编号的,解决1的问题,就在列表前面顶一个数字0,让索引正好对上,在计算的时候,n是几等于长度减-1
这样就可以通过索引的性质i和2i+1之间进行调整了,这时候就构建数
下面就需要调整,要找最后一个结点的叶子结点从它开始调整大顶堆,调整完就能拿到大顶堆了,按照我们例子,就是4321进行调整,调整之后就能得到一个大顶堆,得到大顶堆这才是初始状态,因为你拿到的最大值就是在堆顶的值,,这个值拿到堆的尾巴上去,让最尾部的叶子结点和它对调,对调之后,这个大顶堆就被破坏掉了,然后大顶堆就需要做调整,从堆顶破坏,就从堆顶往下进行调整,这一趟调整完,再形成的大顶堆,堆顶又是你要的最大值,就这样直到只剩一个元素为止,但是可以提前中止,因为剩下两个元素没必要交换了,如果后一个比前一个大就没必要交换了,因为要的是升序
总结》:(每一次都在大顶堆或者小顶堆,拿到一个极值,每一趟都拿到一个极值,这种称为选择排序,选择排序做完就需要做交换,最后也要交换,把最大值找到后,需要放到有序序列里)
时间复杂度(凡是跟二叉树相关的,取复杂度都跟二叉树的取对数相关)以前的事(n2)
是利用堆性质的一种选择排序,在堆顶选出最大值或最小值
时间复杂度
堆排序的时间复杂度O(nlogn)
由于堆排序堆原始记录的排序状态并不敏感,因此它无论是最好,最坏和平均时间复杂度都是O(nlogn)**
红色是平方,绿色是nlogn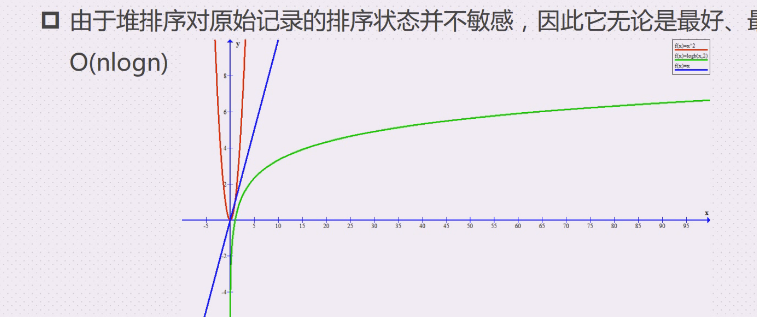
logn太差了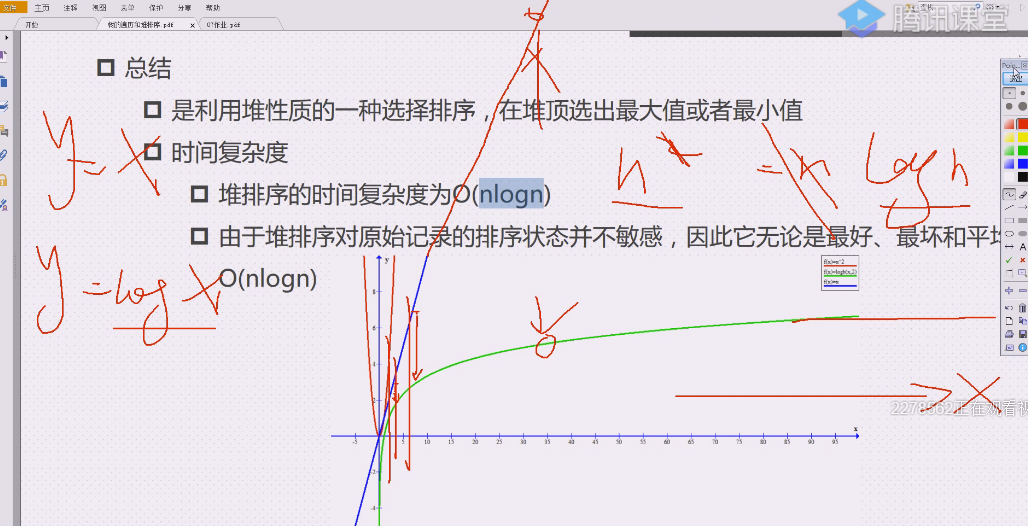
现在是nlogn的问题,nlog n已经是非常好的排序算法了
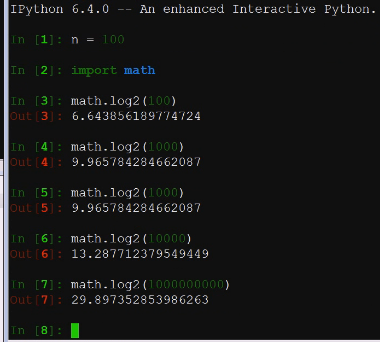
树是一种非常好的数据结构,尤其是在解决排序问题的时候,大大提高了整个计算效率
问二叉树,肯定问B树,B+,红黑
比一下在同样的x下,y需要多少下
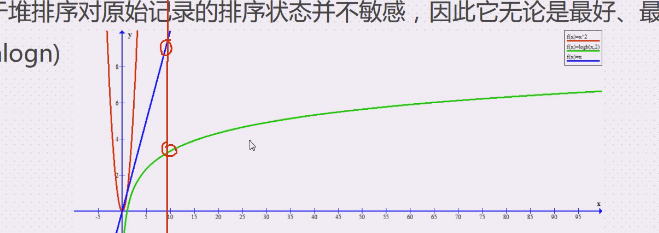

规模增大,算的时间不会增加太快,是一种非常稳定的排序算法,不属于稳定排序,调整的大顶堆可能不一样

**空间复杂度是O(1),这是个常量,你要是1000也人为是1 **
每次得到的大顶堆不一样

图排序比较简单
会问的排序,可能是快速排序,属于交换排序,是一种递归排序,递归排序找中点,以中点为轴,左边右边,左边是比它小的,右边比它大的,在左的一半再找中点,然后再找比他小的
这样就越来越小,最后就把顺序排好了
大多数会问的,冒泡,选择,插入排序(一般手写),快排
最后
以上就是想人陪小蝴蝶最近收集整理的关于2019/10/29 04-堆排序及算法实现的全部内容,更多相关2019/10/29内容请搜索靠谱客的其他文章。








发表评论 取消回复