概述
课程地址：https://www.bilibili.com/video/BV1Kb41127fT
一、引言
数据结构
关于数据组织：DS是ADT的物理实现。解决问题方法的效率，跟数据的组织方式有关
关于空间使用：写一个函数PrintN，打印从1到N的所有整数。解决问题方法的效率，跟空间的利用率有关
代码实现：
//PrintN.c
void PrintN_iteratively(int n) {
for (int i = 1; i <= n; ++i) {
printf("%dn", i);
}
}
void PrintN_recursively(int n) {
if (n) {
PrintN_recursively(n-1);
printf("%dn", n);
}
}
关于算法效率：写程序计算给定多项式在给定点x处的值： f ( x ) = a 0 + a 1 x + . . . + a n − 1 x n − 1 + a n x n f(x) = a_0 + a_1x+...+a_{n-1}x^{n-1}+a_nx^n f(x)=a0+a1x+...+an−1xn−1+anxn
代码实现：
//calculate-polynomial.c
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#define MAXN 10
double f1(int n,double a[],double x);
double f2(int n,double a[],double x);
void testRunTime(double (*func)(int,double*,double),int n,double a[],double x,int cycles);
int main(int argc,char* argv[]){
double x=1.1;
double a[MAXN];
for(int i=0;i<MAXN;++i){
a[i]=i;
}
testRunTime(f1,MAXN-1,a,x,atoi(argv[1]));
testRunTime(f2,MAXN-1,a,x,atoi(argv[1]));
return 0;
}
double f1(int n,double a[],double x){
double p=a[0];
for(int i=1;i<=n;++i){
p=p+a[i]*pow(x,i);
}
return p;
}
double f2(int n,double a[],double x){
double p=a[n];
for(int i=n;i>0;--i){
p=a[i-1]+x*p;
}
return p;
}
void testRunTime(double (*func)(int,double*,double),int n,double a[],double x,int cycles){
clock_t start,stop;
double duration=0;
double ret=0;
start=clock();
for(int i=0;i<cycles;++i){
ret=(*func)(n,a,x);
}
stop=clock();
duration=(double)(stop-start)/CLOCKS_PER_SEC;
printf("function ptr=%p,ret=%f,cycles=%d:ticks=%ld,duration=%fn",func,ret,cycles,stop-start,duration);
}
注意linux下用gcc编译时需要链接数学库-lm
打印函数指针指向的函数的名字很复杂，所以在这里直接打印裸指针来简单区分f1和f2
执行结果：
$ ./02-计算多项式在给定点x的值 1000000
function ptr=0x556bd2284896,ret=84.062575,cycles=1000000:ticks=947014,duration=0.947014
function ptr=0x556bd228491e,ret=84.062575,cycles=1000000:ticks=58210,duration=0.058210
可以看出秦久韶算法确实优于直接算法：解决问题的方法的效率，跟算法的巧妙程度有关
DS：数据对象在计算机中的组织方式
- 逻辑结构：一对一，一对多，多对多；
- 物理存储结构：连续存储，离散存储；
Abstract Data Type：数据对象集+数据集合相关联的操作集
算法
Algorithm：
- 一个有限的指令集
- 接受一些输入（或者没有）
- 产生输出
- 一定在有限步骤后终止
- 每条指令必须明确，在计算机的处理范围之内，不依赖于编程语言
选择排序的伪码描述：
void selection_sort(int* A, int N) {
for (int i = 0; i < N; ++i) {
int min_pos = scan_for_min(A, i, N-1);
swap(A[i], A[min_pos]);
}
}
//A的存储结构采用数组还是链表（虽然看上去很像数组）？
//swap用函数还是宏实现？
//这都不重要
算法的时空复杂度：
递归程序的S(N)=C*N；一般我们关注最坏情况下的复杂度
复杂度的渐进表示：
每当遇到一个O(n^2)的算法，都要本能地想到把它优化成O(n*log(n))的算法
复杂度分析：
最大子列和问题
最大子列和问题：给定N个整数的序列 { A 1 , A 2 , . . . , A N } {A_1, A_2, ..., A_N} {A1,A2,...,AN}，求函数 f ( i , j ) = m a x { 0 , ∑ k = i j A k } f(i, j) = max{0, sum_{k=i}^j{A_k}} f(i,j)=max{0,∑k=ijAk}的最大值
算法1：Time Complexity：O(n^3)
//max-subsequence-sum.c
int MaxSubSeqSum1(int A[], int N) {
int maxSum = 0;
int thisSum = 0;
for (int i = 0; i < N; ++i) {
for (int j = i; j < N; ++j) {
thisSum = 0;
for (int k = i; k < j; ++k) {
thisSum += A[k];
}
if (thisSum > maxSum) maxSum = thisSum;
}
}
return maxSum;
}
改进：对于给定的子列区间[i,j]，不需要用k循环每次都从头算起子列和，只需要每当j向右增加一位时，比较thisSum是否增大了即可，于是得到O(n^2)的算法：
int MaxSubSeqSum2(int A[], int N) {
int maxSum = 0;
int thisSum = 0;
for (int i = 0; i < N; ++i) {
thisSum = 0;
for (int j = i; j < N; ++j) {
thisSum += A[j];
if (thisSum > maxSum) maxSum = thisSum;
}
}
return maxSum;
}
分治法：代码实现参考这里，不深究了
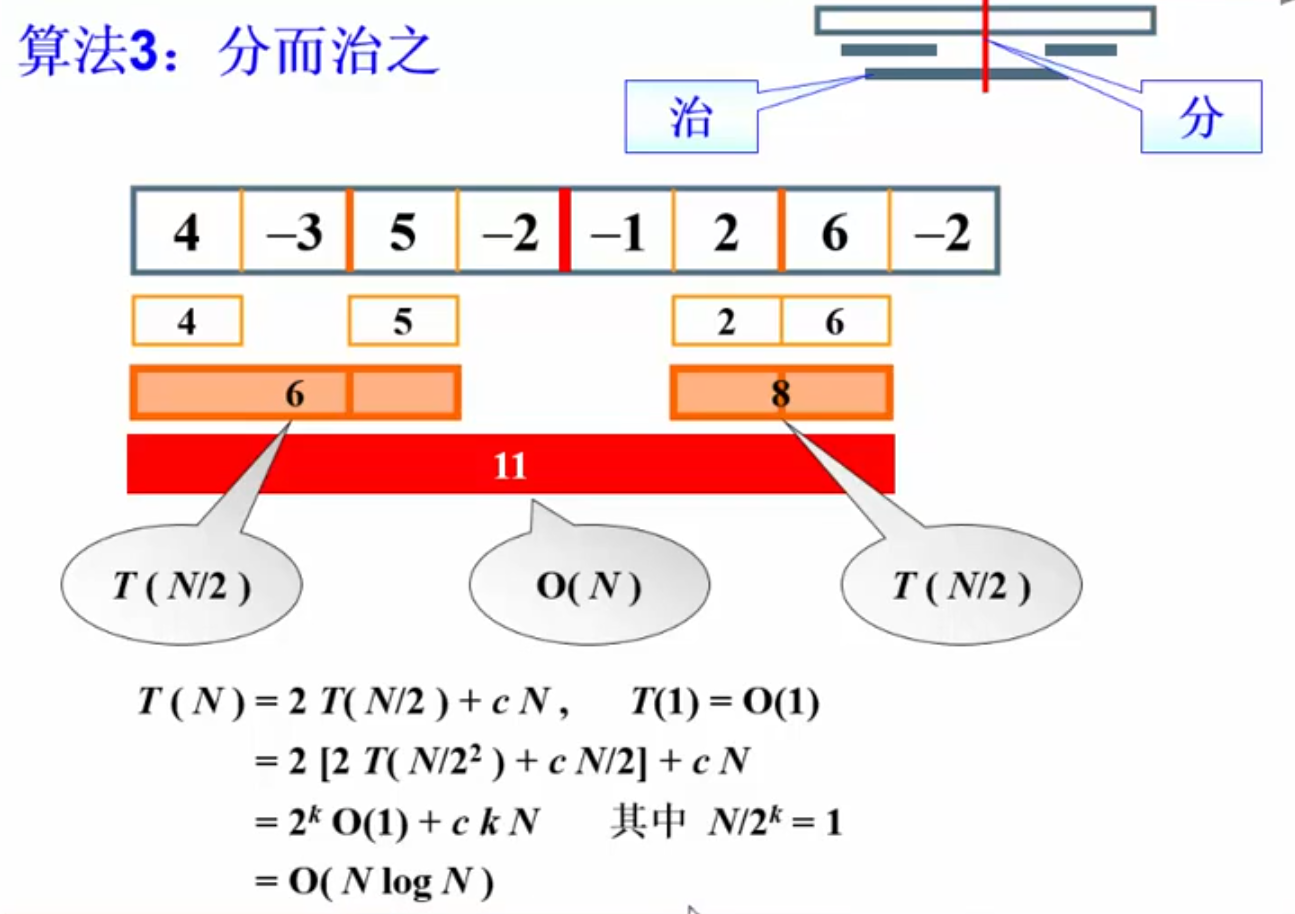
若当前子列和为负，则不可能使后面部分增大，弃之
int MaxSubSeqSum2(int A[], int N) {
int maxSum = 0;
int thisSum = 0;
for (int i = 0; i < N; ++i) {
thisSum = 0;
for (int j = i; j < N; ++j) {
thisSum += A[j];
if (thisSum > maxSum) maxSum = thisSum;
}
}
return maxSum;
}
在线算法：每输入一个数据就进行即时处理，在任何一个地方终止输入，算法都能给出正确的当前的解
二、线性结构
引子-多项式表示
使用顺序存储结构直接表示：数组下标对应指数，数组中的内容对应系数，有很大的空间浪费
使用结构数组：
相加过程：从头开始，比较两个多项式当前对应项的系数
使用链表实现：
代码实现：
typedef struct PolyNode* Polynomial;
struct PolyNode{
int coef;
int expon;
Polynomial link;
};
线性表的顺序存储
线性表：由同类型数据元素构成有序序列的线性结构
线性表的ADT描述：
线性表的顺序存储是利用数组的连续存储空间顺序存放线性表的各元素
代码实现：
//sequential-list.h
#define MAXSIZE 100
#define ERROR -1
typedef int ElementType;
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素的位置 */
};
List MakeEmpty();
Position Find( List L, ElementType X );
bool Insert( List L, ElementType X, Position P );
bool Delete( List L, Position P );
//创建一个空表
List MakeEmpty() {
List l = (List)malloc(sizeof(struct LNode));
l->Last = -1;
return l;
}
//寻找指定元素
Position Find(List l, ElementType x) {
if (l == NULL || l->Last == -1)
return ERROR;
int i = 0;
for (i = 0; i <= l->Last; ++i) {
if (l->Data[i] == x)
break;
}
if (i > l->Last) {
return ERROR;
} else {
return i;
}
}
//插入：在第i个位置插入元素，需要从后往前将元素依次后移一个位置，为待插入的元素腾出空间
bool Insert(List L, ElementType X, Position P) {
if (L == NULL) return false;
if (L->Last == MAXSIZE - 1) {
printf("FULL");
return false;
}
if (P < 0 || P > (L->Last + 1)) {
printf("ILLEGAL POSITION");
return false;
}
for (int i = L->Last; i >= P; --i) {
L->Data[i + 1] = L->Data[i];
}
L->Data[P] = X;
L->Last++;
return true;
}
//删除：将元素依次前移一个位置即可
bool Delete(List L, Position P) {
if (L == NULL)
return false;
if (P < 0 || P > L->Last) {
printf("POSITION %d EMPTY", P);
return false;
}
for (int i = P; i < L->Last; ++i) {
L->Data[i] = L->Data[i + 1];
}
L->Last--;
return true;
}
线性表的链式存储
不要求逻辑上相邻的两个元素物理上也相邻，通过指针建立起数据元素之间的逻辑关系
节点定义与增删查操作集：
//linked-list.h
typedef int ElementType;
typedef struct LNode* List;
struct LNode {
List Next;
ElementType Data;
};
Position Find(List PtrL, ElementType x) {
List p = PtrL;
while (p != NULL && p->Data != x)
p = p->Next;
return p;
}
List Insert(List L, ElementType X, Position P) {
PtrToLNode node = (PtrToLNode) malloc(sizeof(struct LNode));
node->Data = X;
node->Next = NULL;
List header = L;
if (P == L) {
node->Next = L;
return node;
}
while (L) {
if (L->Next == P) {
node->Next = L->Next;
L->Next = node;
return header;
}
L = L->Next;
}
free(node);
printf("Wrong Position for Insertionn");
return ERROR;
}
List Delete(List L, Position P) {
if (P == L) {
PtrToLNode h = L->Next;
free(L);
return h;
}
List header = L;
while (L) {
if (L->Next == P) {
PtrToLNode p = L->Next;
L->Next = p->Next;
free(p);
return header;
}
L = L->Next;
}
printf("Wrong Position for Deletionn");
return ERROR;
}
求表长
//linked-list.h
int Length(List PtrL) {
int j = 0;
List p = PtrL;
while (p) {
p = p->Next;
j++;
}
return j;
}
按序号查找
//linked-list.h
ElementType FindKth(List L, int k) {
int i = 1;
while (L != NULL && i < k) {
L = L->Next;
i++;
}
if (L != NULL && i == k) {
return L->Data;
} else {
return -1;
}
}
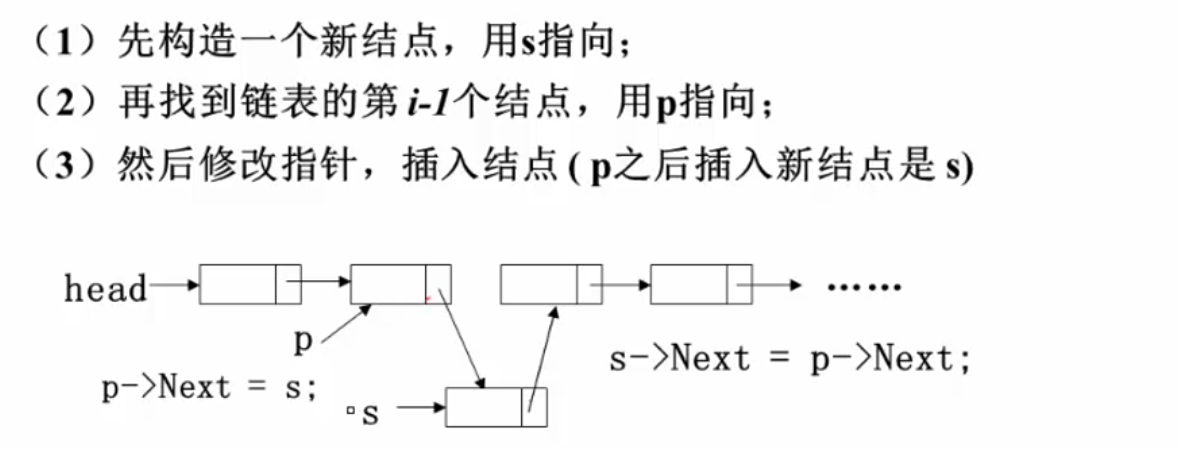
链式存储的插入和删除：
广义表与多重链表
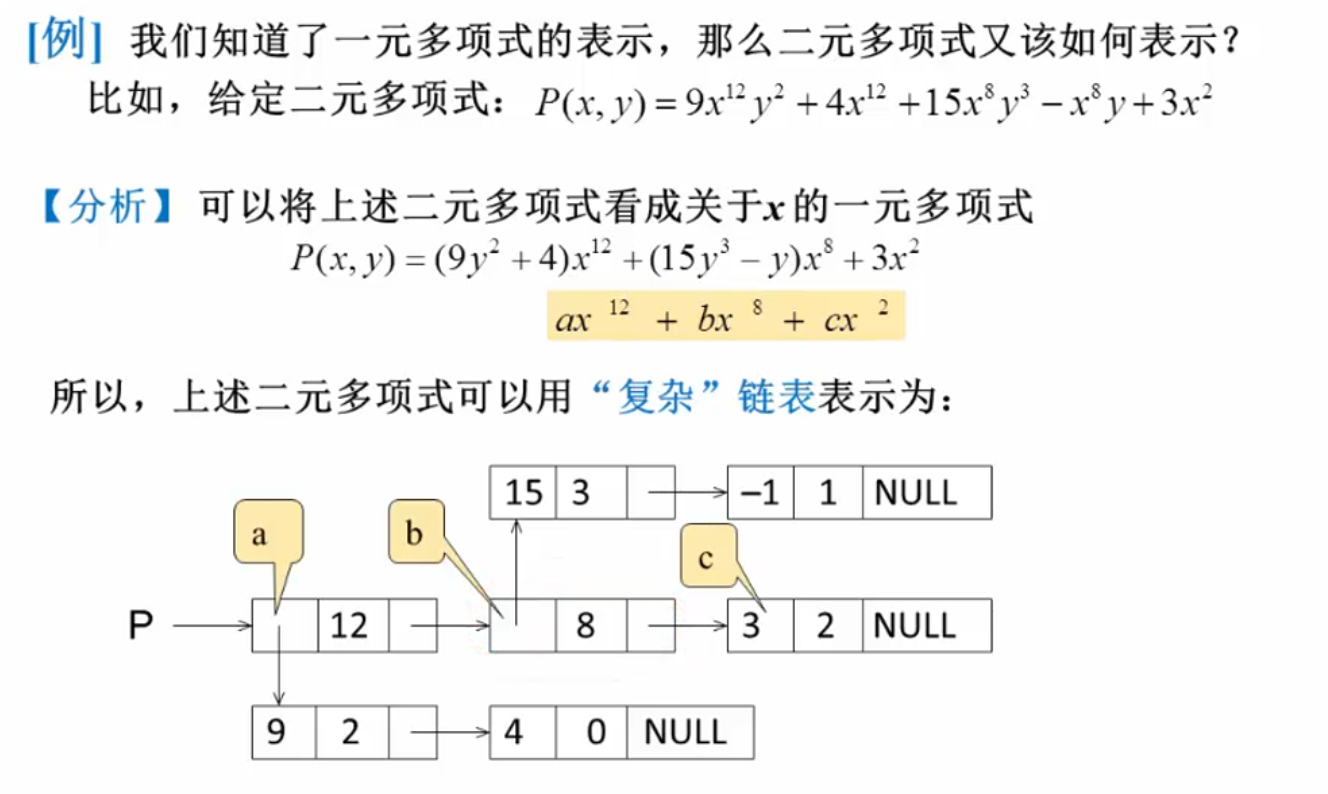
广义表是线性表的推广。对于线性表而言，n个元素都是基本的单元素。在广义表中，这些元素不仅可以是单元素也可以是另一个广义表。
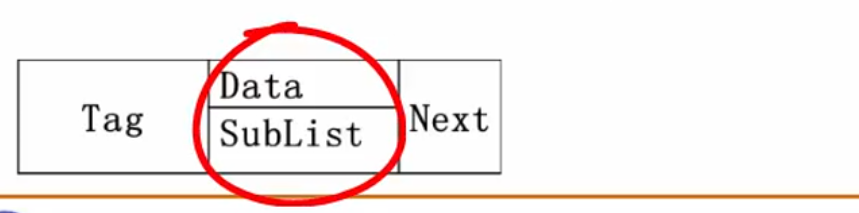
广义表节点定义：
typedef long ElementType;
typedef struct GNode* GList;
struct GNode {
int Tag;
union {
ElementType Data;
GList SubList;
} URegion;
GList Next;
};
使用Tag区分联合中的数据类型
多重链表：
稀疏矩阵的表示问题：
形成的多重链表：
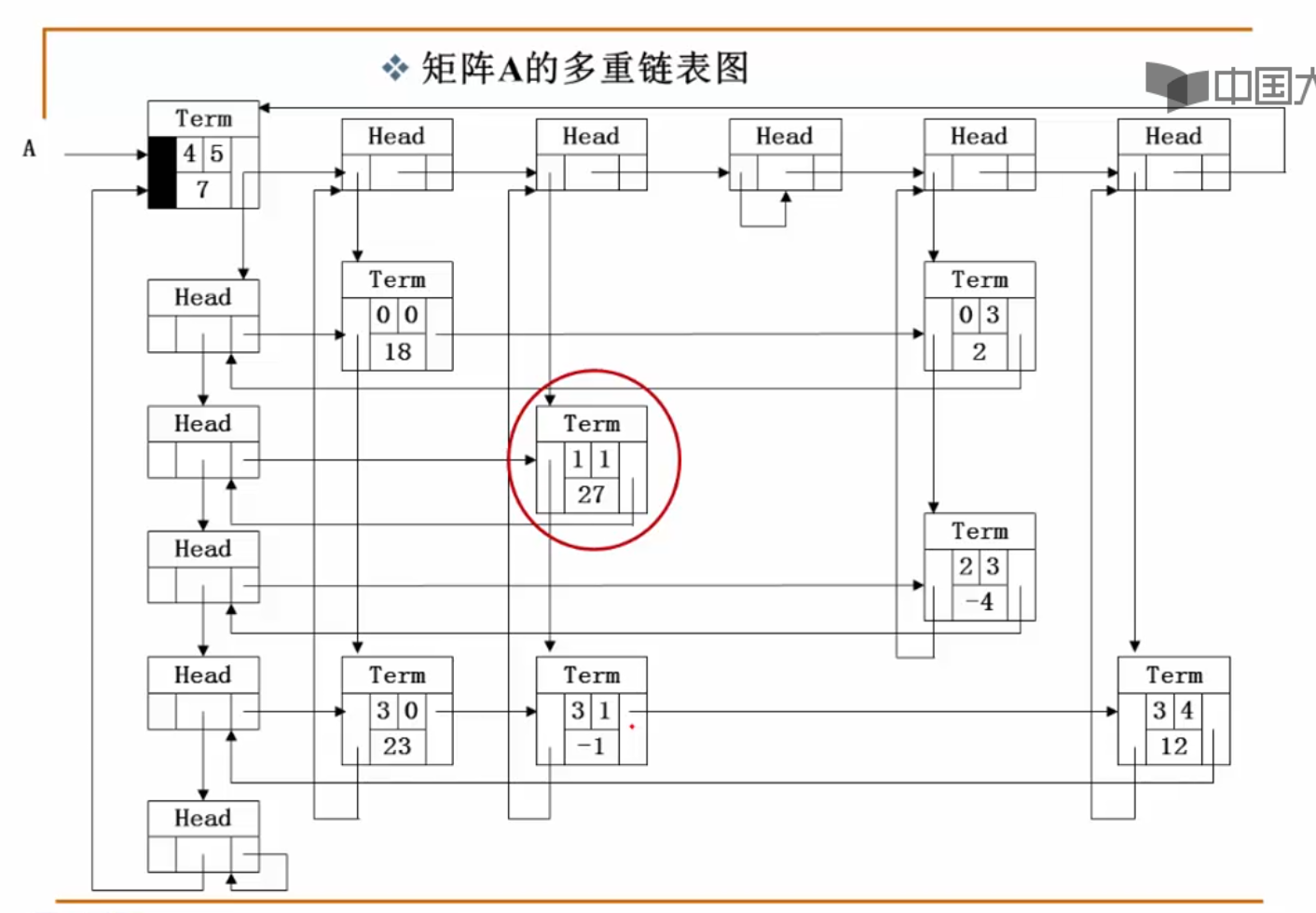
带头结点的链式表操作集
//linked-list-head.h
List MakeEmpty() {
PtrToLNode head = (PtrToLNode) malloc(sizeof(struct LNode));
head->Data = -1;
head->Next = NULL;
return head;
}
Position Find(List L, ElementType X) {
while (L) {
if (L->Data == X) {
return L;
}
L = L->Next;
}
return L;
}
bool Insert(List L, ElementType X, Position P) {
PtrToLNode n = (PtrToLNode) malloc(sizeof(struct LNode));
n->Data = X;
n->Next = NULL;
while (L) {
if (L->Next == P) {
n->Next = P;
L->Next = n;
return true;
}
L = L->Next;
}
free(n);
printf("Wrong Position for Insertionn");
return false;
}
bool Delete(List L, Position P) {
while (L) {
if (L->Next == P) {
PtrToLNode pd = L->Next;
L->Next = pd->Next;
free(pd);
return true;
}
L = L->Next;
}
printf("Wrong Position for Deletionn");
return false;
}
栈
后缀表达式求值问题：
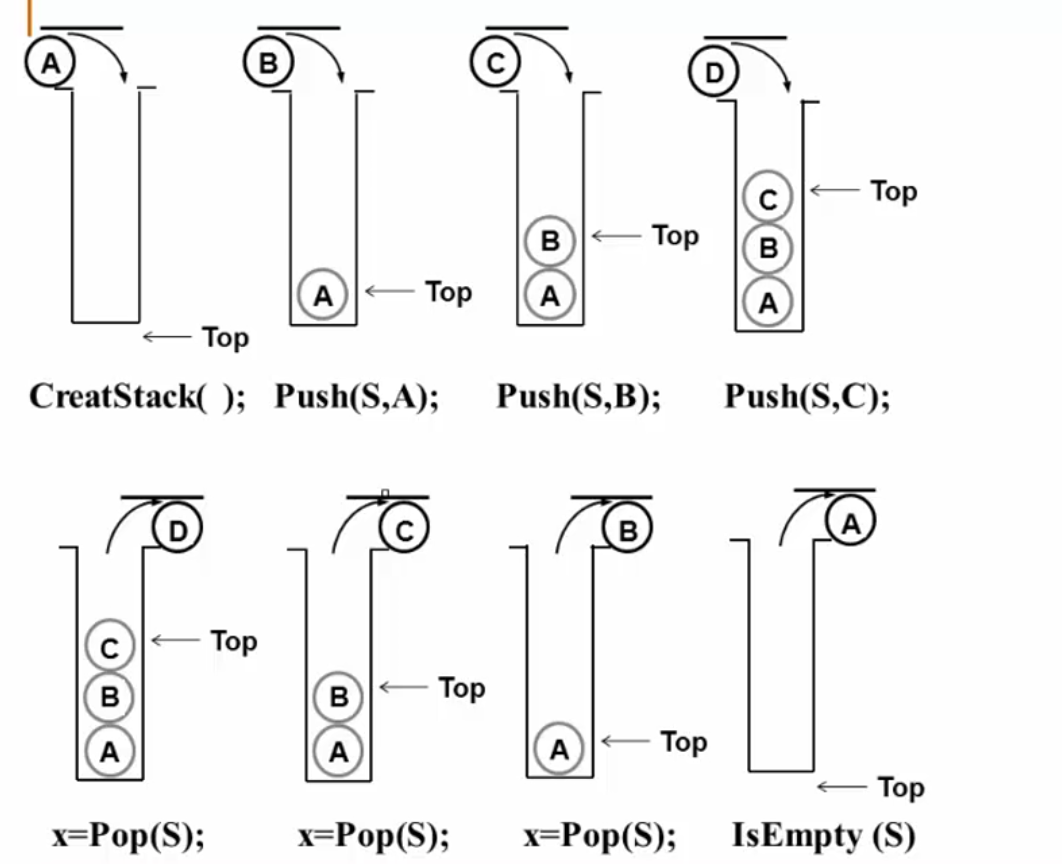
堆栈：具有一定操作约束的线性表，满足LIFO特性
抽象数据类型描述：
操作示例：
栈的顺序存储实现：栈的顺序存储结构通常由一个一维数组和一个记录栈顶位置的变量构成
结构定义和出入栈操作：
//sequential-stack.h
#define MAXSIZE 512
typedef int ElementType;
typedef struct {
ElementType Data[MAXSIZE];
int Top;
} Stack;
bool Push(Stack* PtrS, ElementType item) {
if (PtrS->Top == MAXSIZE - 1) {
return false;
}
PtrS->Data[++(PtrS->Top)] = item;
return true;
}
ElementType Pop(Stack* PtrS) {
if (PtrS->Top == -1) {
return (ElementType)ERROR;
}
return PtrS->Data[(PtrS->Top)--];
}
用一个数组实现两个堆栈：两个栈都从两边往中间生长，当栈顶指针相遇，表示栈满
代码实现：
//double-stack.c
typedef int ElementType;
typedef int Position;
struct SNode {
ElementType *Data;
Position Top1, Top2;
int MaxSize;
};
typedef struct SNode *Stack;
#define ERROR 1e8
Stack CreateStack( int MaxSize ) {
Stack s = (Stack)malloc(sizeof(struct SNode));
if (s) {
s->Data = (ElementType*)malloc(sizeof(ElementType) * MaxSize);
s->Top1 = -1;
s->Top2 = MaxSize;
s->MaxSize = MaxSize;
}
return s;
}
bool Push( Stack S, ElementType X, int Tag ){
if (S->Top2 - S->Top1 == 1) {
printf("Stack Fulln");
return false;
}
if (Tag == 1) {
S->Data[++(S->Top1)] = X;
return true;
}
if (Tag == 2) {
S->Data[--(S->Top2)] = X;
return true;
}
}
ElementType Pop( Stack S, int Tag ) {
if (Tag == 1) {
if (S->Top1 == -1) {
printf("Stack 1 Emptyn");
return ERROR;
} else {
ElementType t = S->Data[(S->Top1)--];
return t;
}
}
if (Tag == 2) {
if (S->Top2 == S->MaxSize) {
printf("Stack 2 Emptyn");
return ERROR;
} else {
ElementType t = S->Data[(S->Top2)++];
return t;
}
}
}
栈的链式存储实现：栈的链式存储结构实际上就是一个单链表，叫做链栈。push和pop都在表头进行。链栈几乎不会存在栈满的问题，所以其相比于顺序存储的栈更好用
结构定义和操作集实现：
//linked-stack.h
#ifndef LINKED_STACK_H
#define LINKED_STACK_H
#include <stdlib.h>
#include <limits.h>
typedef int ElementType;
#define ERROR INT_MIN
struct SNode {
ElementType Data;
struct SNode* Next;
};
typedef struct SNode SNode;
typedef SNode* Stack;
//创建（一个带头结点的单链表）
Stack CreateStack() {
Stack s;
s = (Stack)malloc(sizeof(SNode));
s->Next = NULL;
return s;
}
//判断是否为空
int StackIsEmpty(Stack s) { return (s->Next == NULL); }
void Push(ElementType item, Stack s) {
SNode* t = (SNode*)malloc(sizeof(SNode));
t->Data = item;
t->Next = s->Next;
s->Next = t;
}
ElementType Pop(Stack s) {
SNode* firstCell;
ElementType topElem;
if (StackIsEmpty(s)) {
return (ElementType)ERROR;
}
firstCell = s->Next;
s->Next = firstCell->Next;
topElem = firstCell->Data;
free(firstCell);
return topElem;
}
ElementType Top(Stack s) {
if (StackIsEmpty(s)) {
return (ElementType)ERROR;
} else {
return s->Next->Data;
}
}
void DestoryStack(Stack S) {
if (S != NULL) {
while (!StackIsEmpty(S)) {
Pop(S);
}
free(S);
}
}
#endif
表达式求值问题
题目列表：
150. 逆波兰表达式求值
面试题 16.26. 计算器
224. 基本计算器
表达式转换
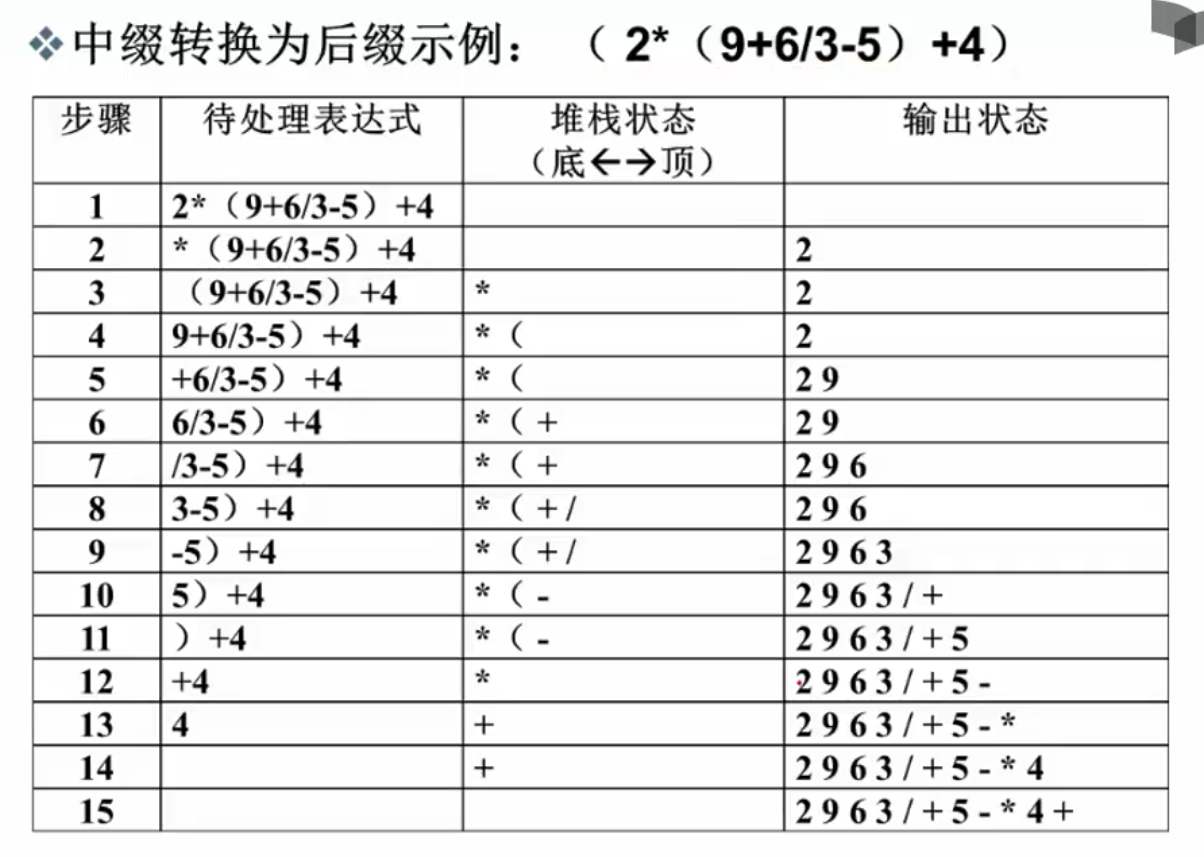
中缀表达式转后缀表达式：
一个示例：
中缀表达式转后缀表达式：
转化示例：
堆栈的其他应用：
- 函数调用和递归
- 回溯算法
- 深度优先搜索
队列
队列：具有一定操作约束的线性表，只能在一端插入，在另一端删除
队列的ADT描述：
结构定义：
//sequential-queue.h
#define MAXSIZE 1024
#define ElementType int
struct QNode {
ElementType Data[MAXSIZE];
int front;
int rear;
};
typedef struct QNode* Queue;
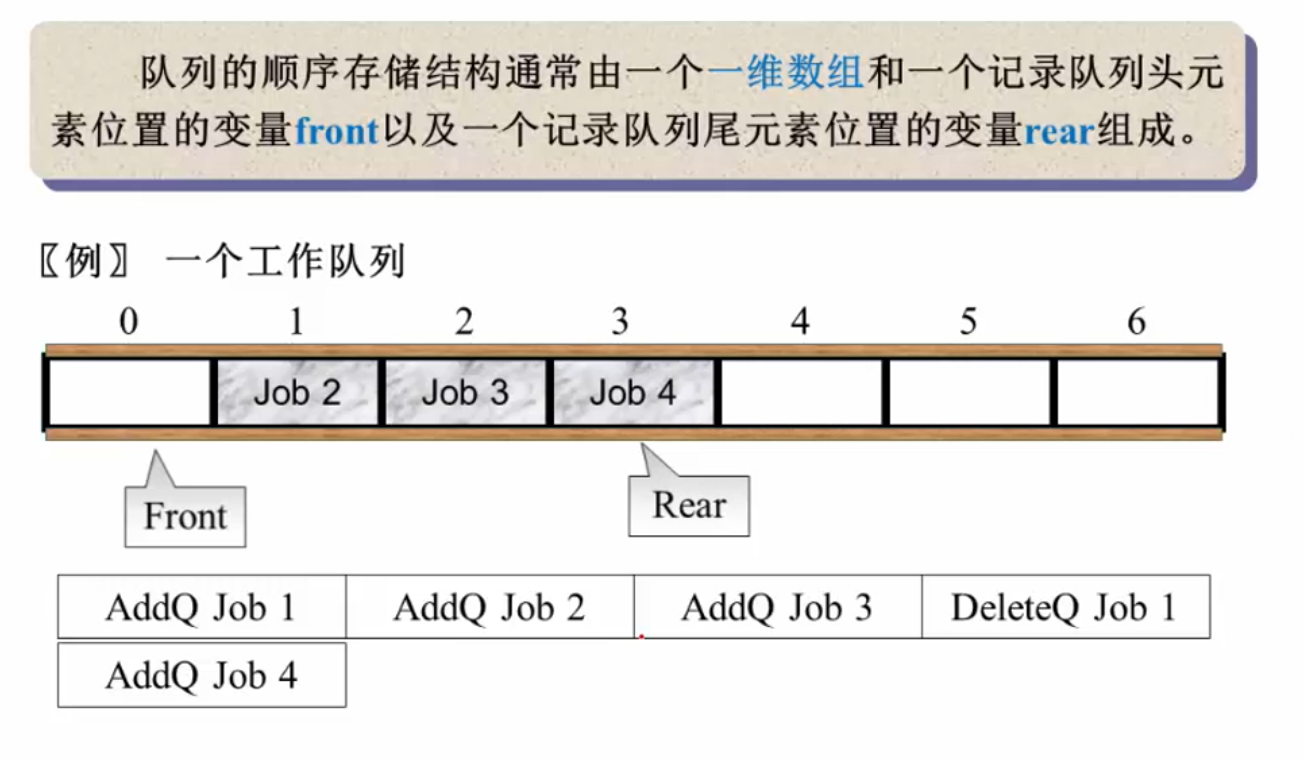
但是线性数组存在无法充分利用前面空间的问题，改用循环队列实现：
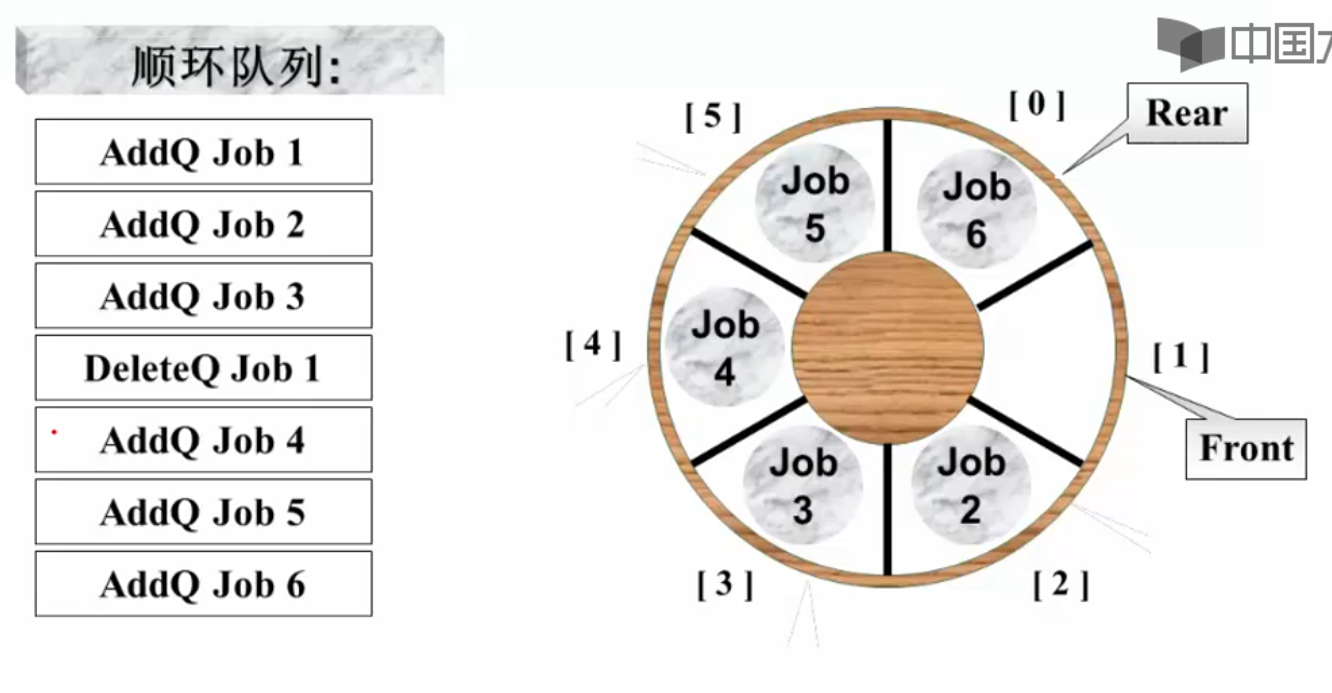
front指向队头元素的前一个位置，rear指向队尾元素。为了简化操作，牺牲一个空间不存数据，方便判断队列满，否则队列空和队列满都对应front==rear
操作实现：
//sequential-queue.h
Queue CreateQueue() {
Queue q = (Queue)malloc(sizeof(QNode));
q->front = q->rear = 0;
return q;
}
bool EnQueue(Queue PtrQ, ElementType item) {
if ((PtrQ->rear + 1) % MAXSIZE == PtrQ->front) {
//队列满
return false;
}
PtrQ->rear = (PtrQ->rear + 1) % MAXSIZE;
PtrQ->Data[PtrQ->rear] = item;
return true;
}
ElementType DeQueue(Queue PtrQ) {
if (PtrQ->rear == PtrQ->front) {
//队列空
return (ElementType)-1;
} else {
PtrQ->front = (PtrQ->front + 1) % MAXSIZE;
return PtrQ->Data[PtrQ->front];
}
}
void DestoryQueue(Queue PtrQ) {
if (PtrQ != NULL)
free(PtrQ);
}
队列的链式存储实现：采用一个单链表实现，插入在链表尾，删除在链表头。因为若删除在链表尾，会导致rear无法找到前驱
结构定义：
//linked-queue.h
typedef int ElementType;
struct Node {
ElementType Data;
struct Node* Next;
};
struct QNode {
struct Node* front;
struct Node* rear;
};
typedef struct QNode* Queue;
操作实现：
//linked-queue.h
Queue CreateQueue() {
Queue q = (Queue)malloc(sizeof(struct QNode));
q->front = q->rear = NULL;
return q;
}
void EnQueue(Queue PtrQ, ElementType item) {
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->Data = item;
if (PtrQ->front == NULL) {
PtrQ->front = PtrQ->rear = newNode;
return;
} else {
PtrQ->rear->Next = newNode;
PtrQ->rear = newNode;
return;
}
}
bool isQueueEmpty(Queue PtrQ) {
return PtrQ->front == NULL;
}
ElementType DeQueue(Queue PtrQ) {
struct Node* frontCell;
ElementType ret;
//空队列
if (PtrQ->front == NULL) {
return (ElementType)-1;
}
frontCell = PtrQ->front;
if (PtrQ->front == PtrQ->rear)
PtrQ->front = PtrQ->rear = NULL;
else
PtrQ->front = PtrQ->front->Next;
ret = frontCell->Data;
free(frontCell);
return ret;
}
void DestoryQueue(Queue PtrQ) {
if (PtrQ != NULL) {
while (DeQueue(PtrQ) != -1)
;
free(PtrQ);
}
}
多项式加法运算
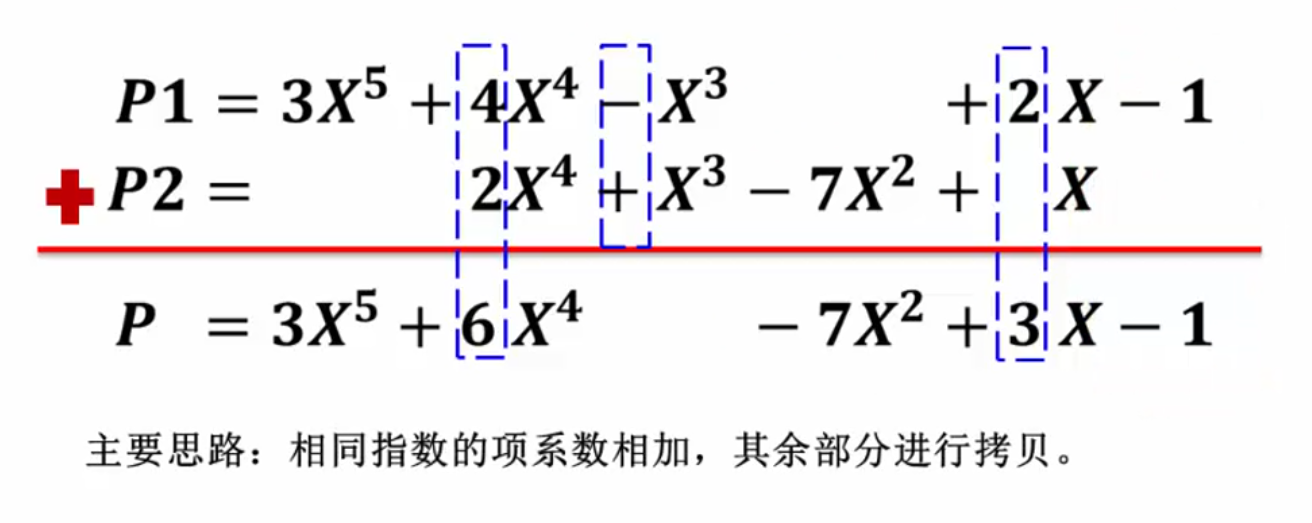
采用单链表表示：
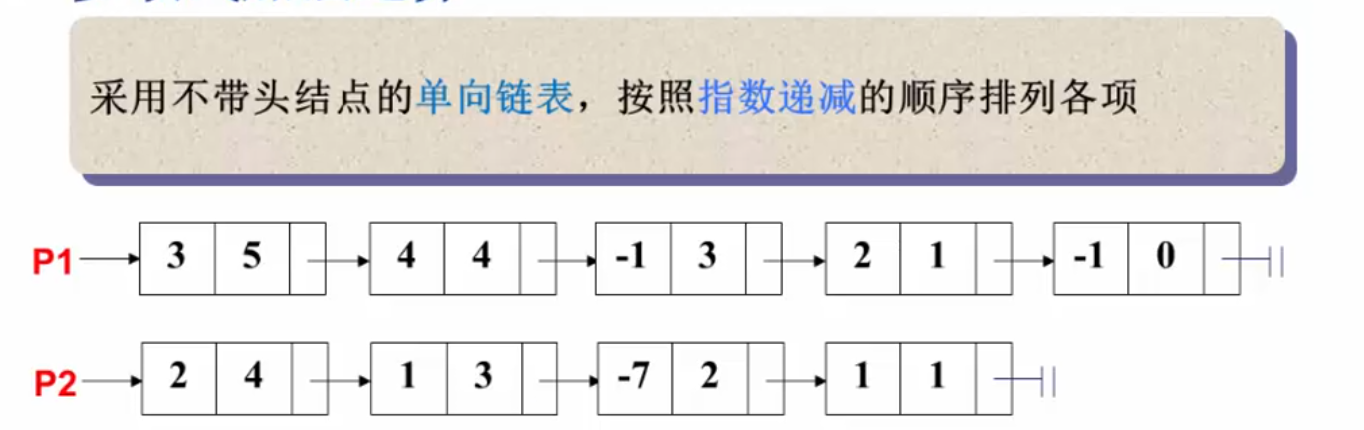
结构定义：
//polynomial-add-and-multiply.c
#include <stdio.h>
#include <stdlib.h>
struct PolyNode {
int coef;
int expon;
struct PolyNode* next;
};
typedef struct PolyNode* Polynomial;
Polynomial PolyAdd(Polynomial P1, Polynomial P2);
int Compare(int e1, int e2);
void Attach(int coef, int expon, Polynomial* pRear);
Polynomial ReadPoly();
Polynomial PolyMult(Polynomial P1, Polynomial P2);
void PrintPoly(Polynomial P);
算法思路，类似于归并：
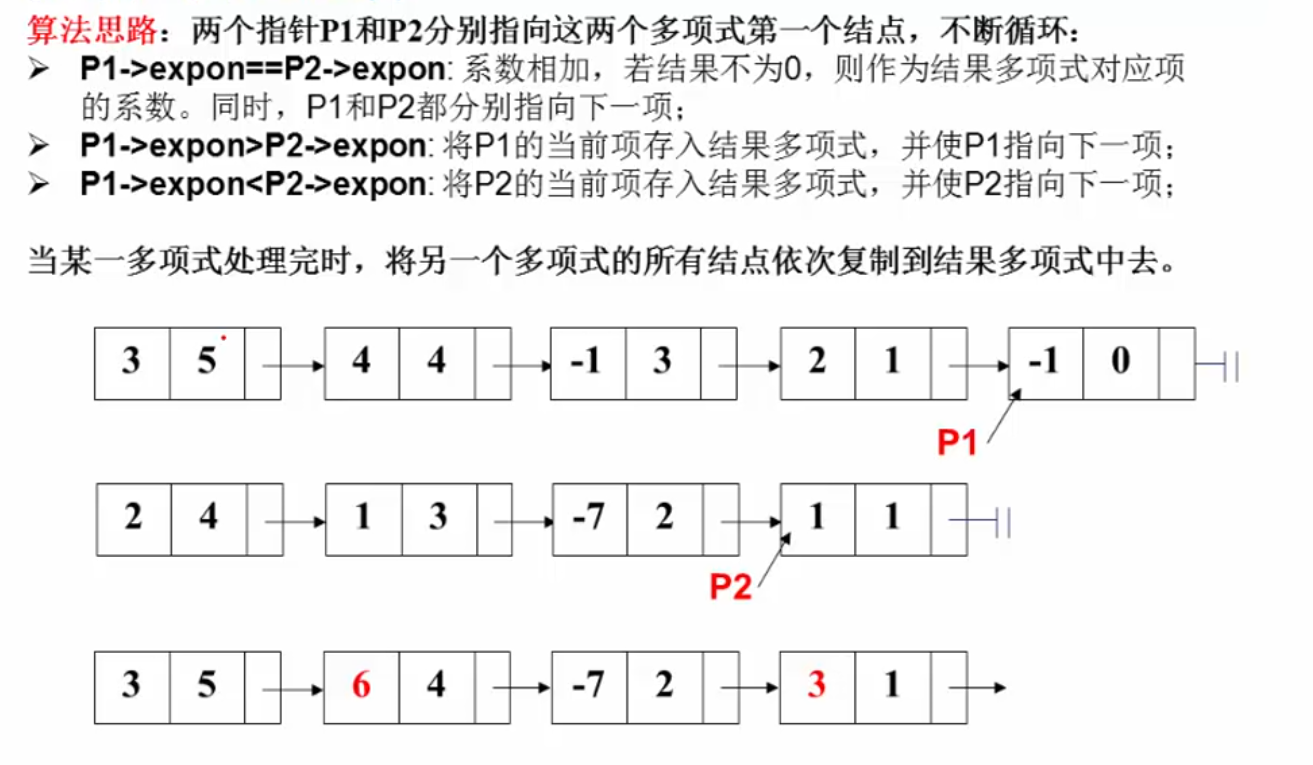
代码实现：
Polynomial PolyAdd(Polynomial P1, Polynomial P2) {
Polynomial front, rear, temp;
int sum = 0;
rear = (struct PolyNode*)malloc(sizeof(struct PolyNode));
front = rear;
while (P1 && P2) {
switch (Compare(P1->expon, P2->expon)) {
case 1:
Attach(P1->coef, P1->expon, &rear);
P1 = P1->next;
break;
case -1:
Attach(P2->coef, P2->expon, &rear);
P2 = P2->next;
break;
case 0:
sum = P1->coef + P2->coef;
if (sum)
Attach(sum, P1->expon, &rear);
P1 = P1->next;
P2 = P2->next;
break;
default:
break;
}
}
while (P1) {
Attach(P1->coef, P1->expon, &rear);
P1 = P1->next;
}
while (P2) {
Attach(P2->coef, P2->expon, &rear);
P2 = P2->next;
}
rear->next = NULL;
temp = front;
front = front->next;
free(temp);
return front;
}
int Compare(int e1, int e2) {
if (e1 > e2)
return 1;
else if (e1 < e2)
return -1;
else
return 0;
}
void Attach(int coef, int expon, Polynomial* pRear) {
Polynomial P = (Polynomial)malloc(sizeof(struct PolyNode));
P->coef = coef;
P->expon = expon;
P->next = NULL;
(*pRear)->next = P;
(*pRear) = P;
}
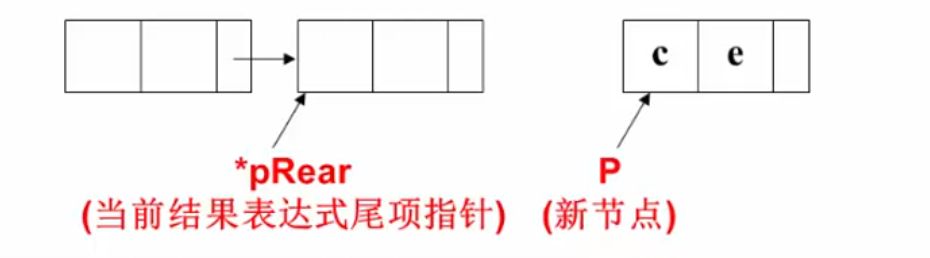
多项式乘法与加法运算
求解思路：
- 多项式表示
- 程序框架
- 读多项式
- 加法实现
- 乘法实现
- 多项式输出
多项式的表示，与上一节的相同：
struct PolyNode {
int coef;
int expon;
struct PolyNode* next;
};
typedef struct PolyNode* Polynomial;
程序框架的搭建：
读入多项式的函数，两点需要注意：
- 尾插单链表时，rear指针要传地址，也就是二级指针，因为函数中要修改rear的指向。
- 为了不在每次处理时都判别
rear==NULL，提前申请一个节点，提高效率。
代码实现：
Polynomial ReadPoly() {
int c, e, N;
Polynomial rear, t;
scanf("%d", &N);
Polynomial P = (Polynomial)malloc(sizeof(struct PolyNode));
P->next = NULL;
rear = P;
while (N--) {
scanf("%d %d", &c, &e);
Attach(c, e, &rear);
}
t = P;
P = P->next;
free(t);
return P;
}
采用第二种方式，代码实现：
Polynomial PolyMult(Polynomial P1, Polynomial P2) {
if (!P1 || !P2)
return NULL;
Polynomial P, rear, t1, t2, t;
int c, e;
t1 = P1;
t2 = P2;
P = (Polynomial)malloc(sizeof(struct PolyNode));
P->next = NULL;
rear = P;
// t1的第一项乘以t2的每一项
while (t2) {
Attach(t1->coef * t2->coef, t1->expon + t2->expon, &rear);
t2 = t2->next;
}
t1 = t1->next;
while (t1) {
t2 = P2;
rear = P;
while (t2) {
c = t1->coef * t2->coef;
e = t1->expon + t2->expon;
while (rear->next && rear->next->expon > e)
rear = rear->next;
//指数相等，系数合并
if (rear->next && rear->next->expon == e) {
if (rear->next->coef + c) {
//系数合并后!=0
rear->next->coef += c;
} else {
//系数合并后==0
t = rear->next;
rear->next = t->next;
free(t);
}
} else {
t = (Polynomial)malloc(sizeof(struct PolyNode));
t->coef = c;
t->expon = e;
t->next = rear->next;
rear->next = t;
rear = rear->next;
}
t2 = t2->next;
}
t1 = t1->next;
}
t2 = P;
P = P->next;
free(t2);
return P;
}
打印输出多项式：
void PrintPoly(Polynomial P) {
if (!P) {
printf("0 0n");
return;
}
int flag = 0;
while (P) {
if (!flag) {
flag = 1;
} else {
printf(" ");
}
printf("%d %d", P->coef, P->expon);
P = P->next;
}
printf("n");
}
逆转链表
抽象链表的表示：
代码实现：
List Reverse(List L) {
PtrToNode d = (PtrToNode) malloc(sizeof(struct Node));
d->Next = 0;
PtrToNode p = L;
PtrToNode q;
while (p) {
q = p->Next;
p->Next = d->Next;
d->Next = p;
p = q;
}
PtrToNode ret = d->Next;
free(d);
return ret;
}
剑指 Offer 24. 反转链表
三、树
顺序查找与二分查找
Searching：
顺序查找代码实现：
int SequentialSearch(List Tbl, ElementType K) {
//0号元素设立为哨兵
Tbl->Element[0] = K;
int i = 0;
//这样就不必每次都判断是否到达i==0，循环到i=0必定会退出
for (i = Tbl->length; Tbl->Element[i] != K; --i);
return i;
}
Time Complexity：O(n)
Binary Search：
代码实现：
int BinarySearch(List Tbl, ElementType K) {
int left = 1;
int right = Tbl->Last;
int mid = 0;
while (left <= right) {
mid = (left + right) >> 1;
if (K == Tbl->Data[mid]) {
return mid;
} else if (K > Tbl->Data[mid]) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return NotFound;
}
Time Complexity:O(logn)
二分查找判定树：
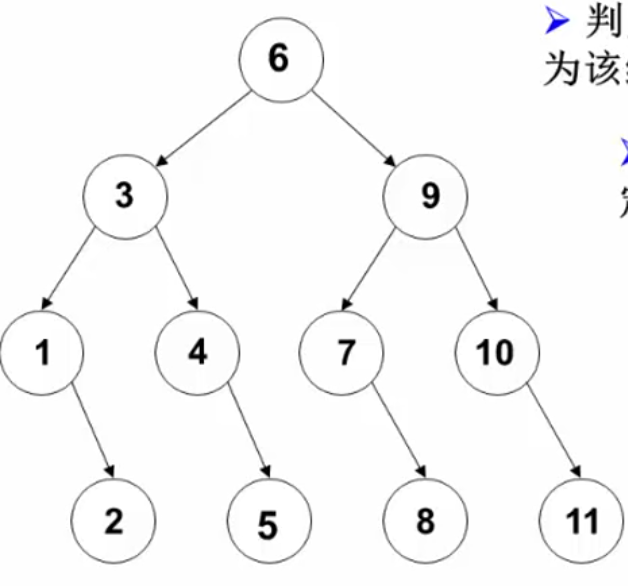
判定树上每个节点需要查找的次数刚好为该节点所在的层数
查找成功时的查找次数不会超过判定树的深度：[log2n+1]
力扣二分查找练习：35. 搜索插入位置
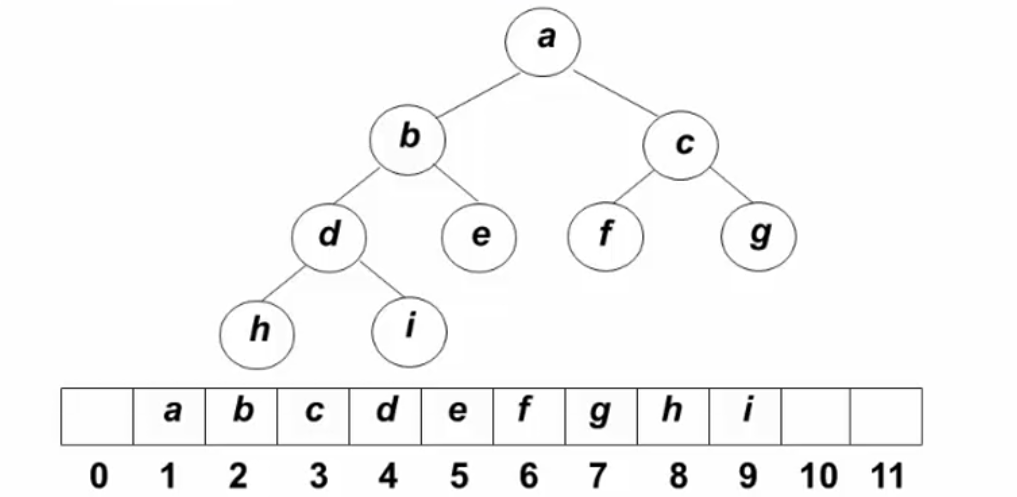
树的定义和表示
树的定义：
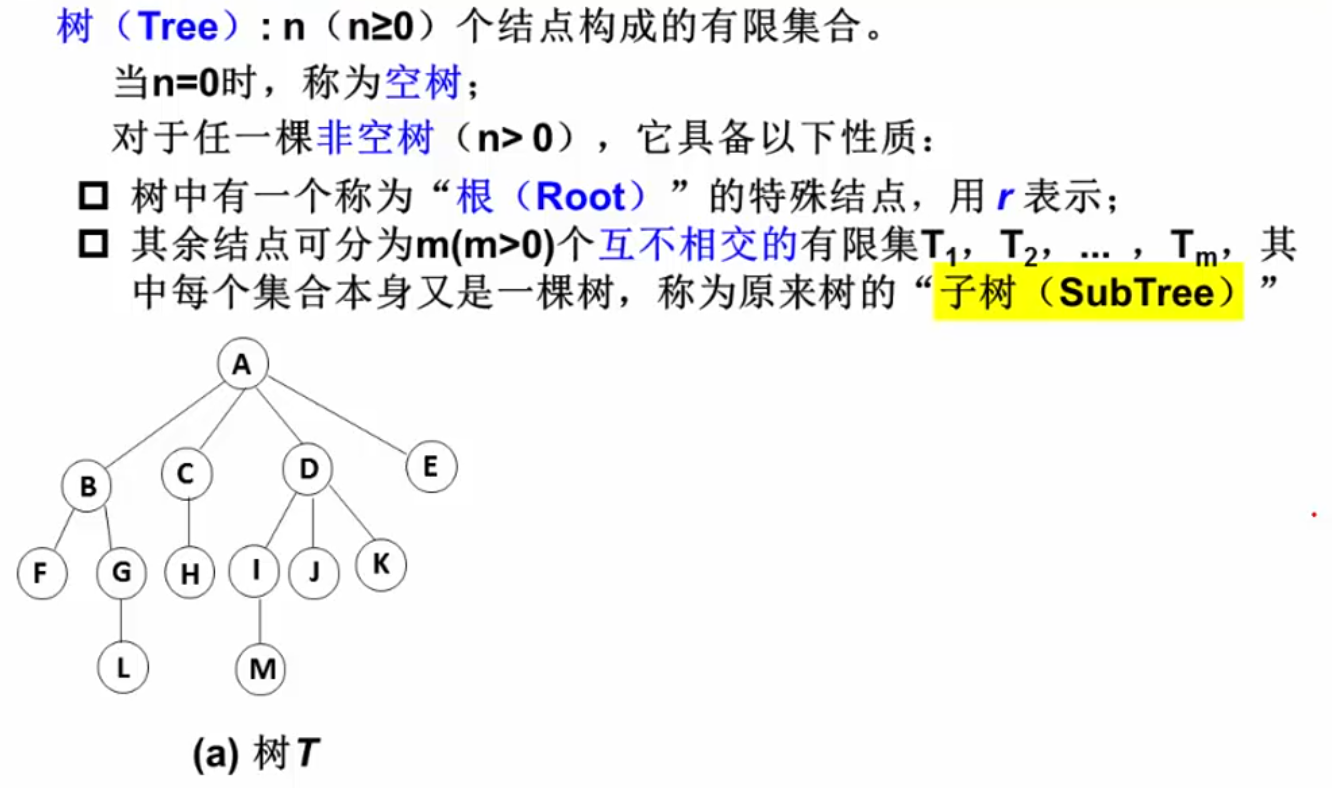
- 除了根节点外，每个节点都有且仅有一个根节点
- 一棵N个节点的树有N-1条边
- 树是保证节点连通的最小连接方式
树的基本术语：
- 节点的度：节点子树的个数
- 树的度：树的所有节点中最大的度数
- 叶节点：度=0的节点
树的表示：
儿子兄弟表示法：
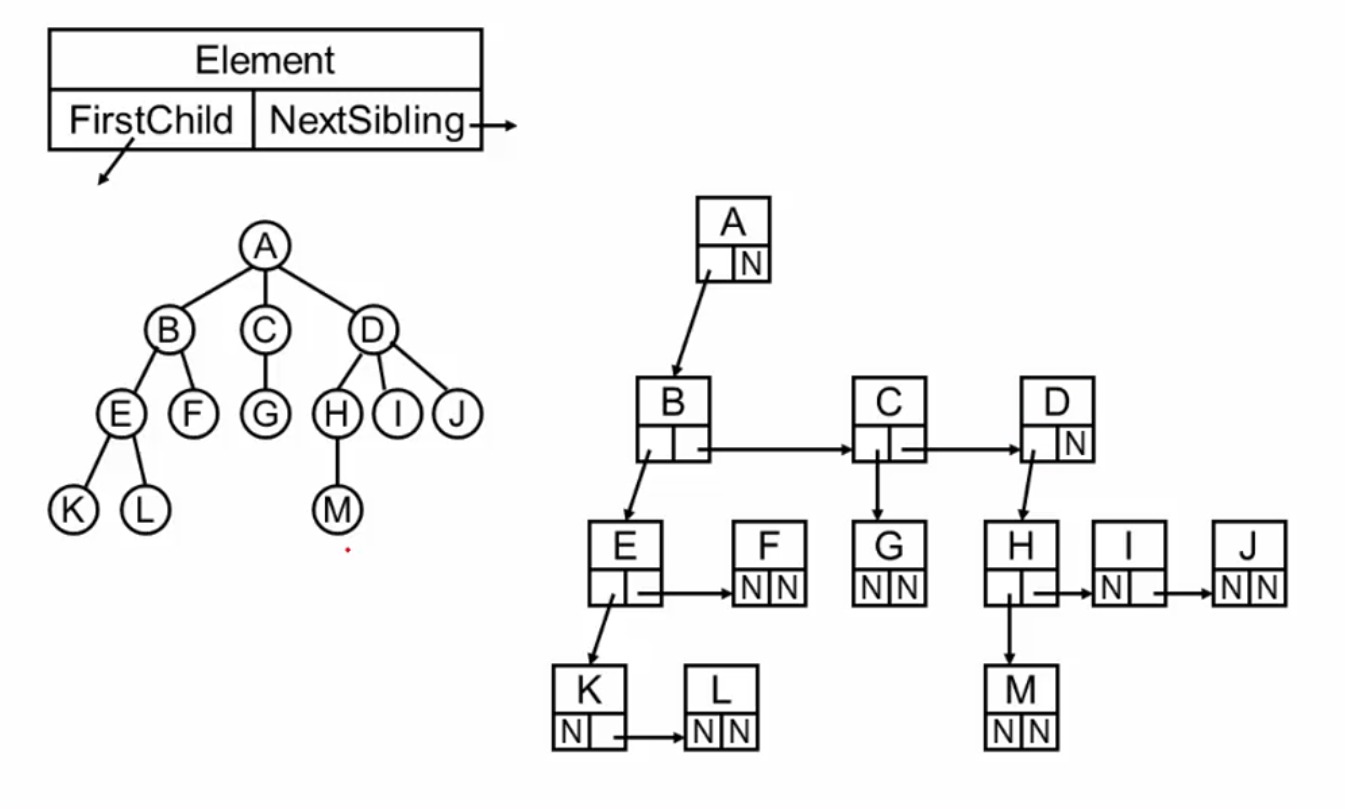
将儿子兄弟表示法旋转45度，就得到一棵二叉树：
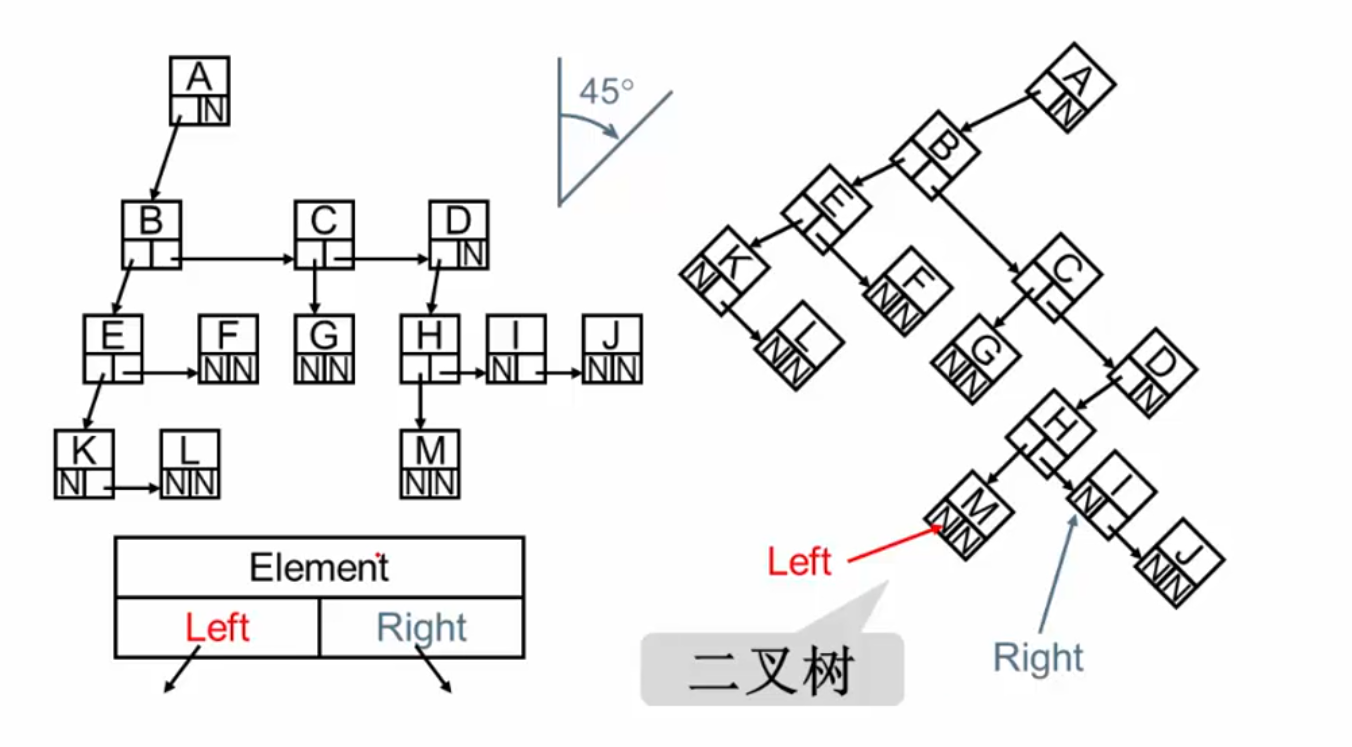
二叉树
二叉树：一个有穷的节点集合，这个集合可以为空
若不为空，则他是由根节点和称为其左子树和右子树的两棵不相交的子树组成
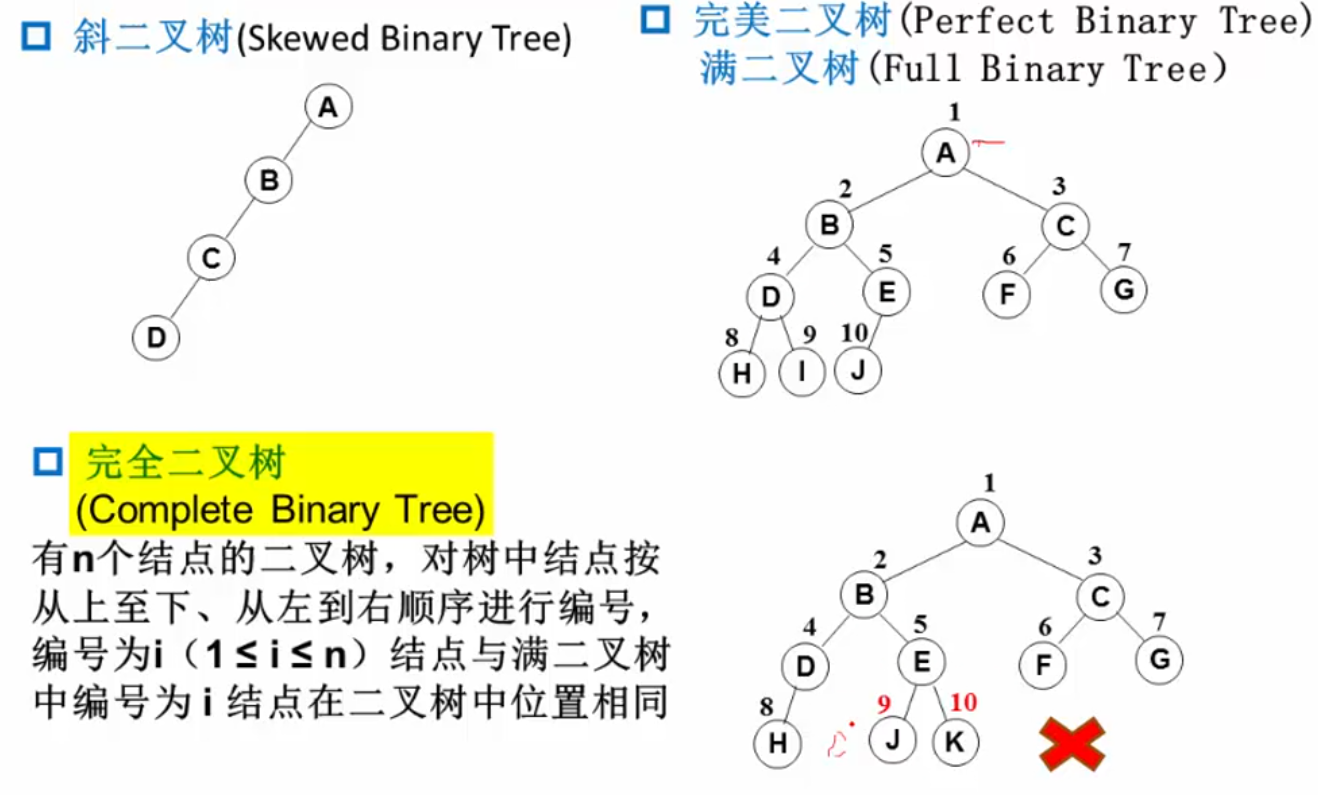
斜二叉树，满二叉树，完全二叉树：
二叉树的性质：
- 第i层的最大节点数为 2 i − 1 2^{i-1} 2i−1
- 深度为k的二叉树的最大节点数为 2 k − 1 2^k-1 2k−1
- 对于任何二叉树： n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1
二叉树的ADT定义：
遍历方法：
void InorderTraversal( BinTree BT ); //先序：根-左-右
void PreorderTraversal( BinTree BT ); //中序：左-根-右
void PostorderTraversal( BinTree BT ); //后序：左-右-根
void LevelorderTraversal( BinTree BT ); //层序：从左到右，从上到下
二叉树的存储结构：
顺序存储：
完全二叉树：从上到下，从左到右顺序存储。
节点的父子关系：
但是对于一般的二叉树，会造成空间浪费：
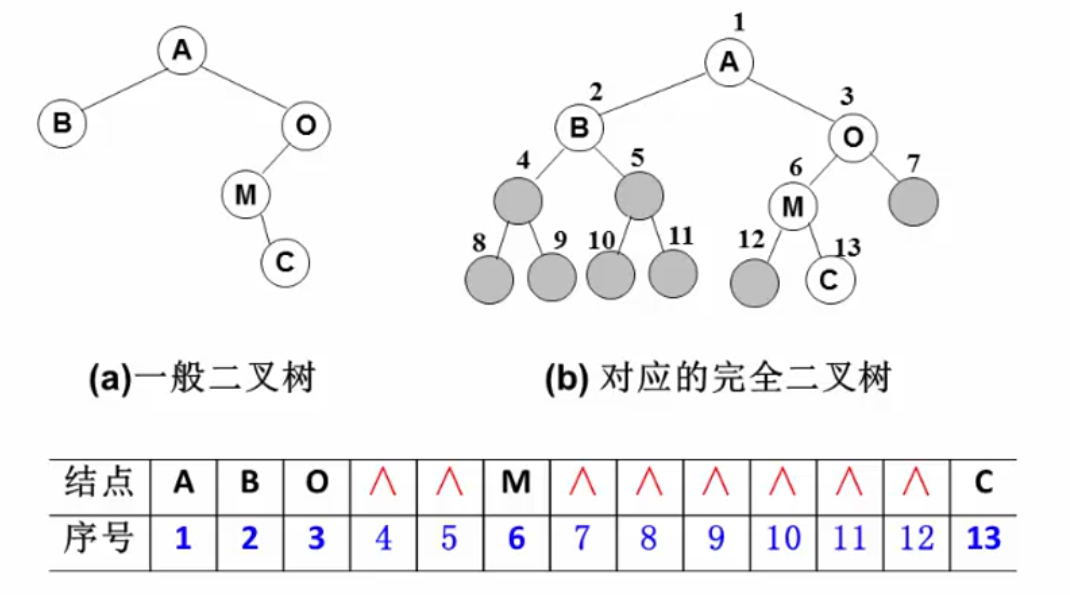
链表存储：
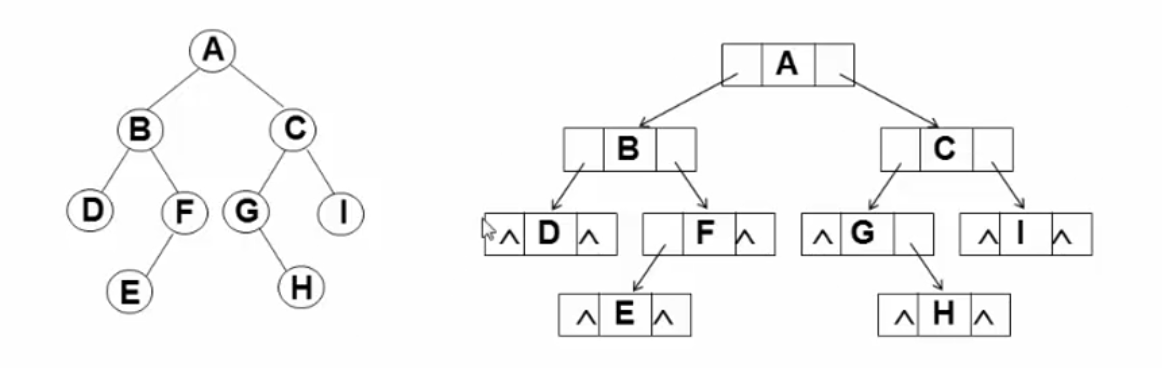
代码实现：
typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
二叉树的遍历
先序遍历：
- 首先访问根节点
- 先序遍历其左子树
- 先序遍历其右子树
代码实现：
//binary-tree-traversal-r.c
void PreorderTraversal(BinTree BT) {
if (BT) {
printf(" %c", BT->Data);
PreorderTraversal(BT->Left);
PreorderTraversal(BT->Right);
}
}
中序遍历：
//binary-tree-traversal-r.c
void InorderTraversal(BinTree BT) {
if (BT) {
InorderTraversal(BT->Left);
printf(" %c", BT->Data);
InorderTraversal(BT->Right);
}
}
遍历结果序列：DBEFAGHCI
后序遍历：
//binary-tree-traversal-r.c
void PostorderTraversal(BinTree BT) {
if (BT) {
PostorderTraversal(BT->Left);
PostorderTraversal(BT->Right);
printf(" %c", BT->Data);
}
}
遍历结果序列：DEFBHGICA
三种遍历所经过的路线是一样的，只是访问各个节点的时机不同：
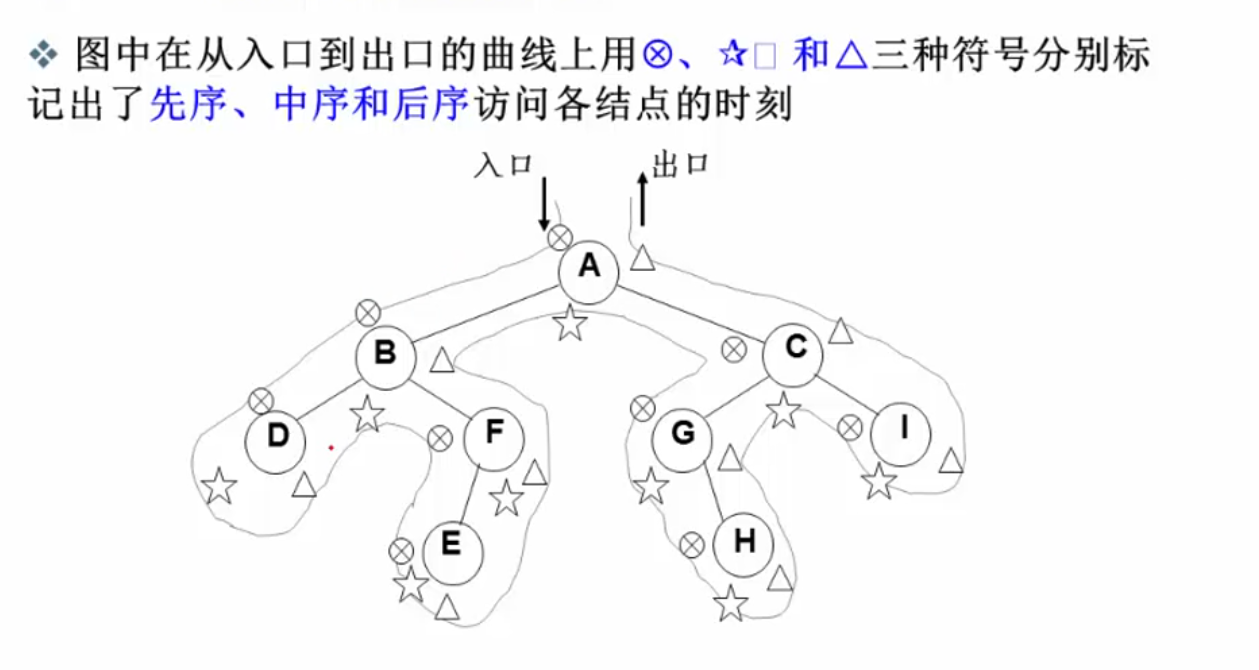
非递归遍历：
使用stack：
- 遇到一个节点，将其压栈，并去遍历它的左子树
- 左子树遍历结束后，从栈顶弹出这个节点并访问他
- 然后按其右指针再去中序遍历该节点的右子树
//binary-tree-traversal-nr.c
#define MAXN 1001
void InorderTraversal(BinTree BT) {
BinTree* stack = (BinTree*)malloc(sizeof(BinTree) * MAXN);
int top = -1;
while (BT || top != -1) {
while (BT) {
stack[++top] = BT;
BT = BT->Left;
}
if (top != -1) {
BT = stack[top--];
printf(" %c", BT->Data);
BT = BT->Right;
}
}
free(stack);
}
void PreorderTraversal(BinTree BT) {
BinTree* stack = (BinTree*)malloc(sizeof(BinTree) * MAXN);
int top = -1;
while (BT || top != -1) {
while (BT) {
printf(" %c", BT->Data);
stack[++top] = BT;
BT = BT->Left;
}
if (top != -1) {
BT = stack[top--];
BT = BT->Right;
}
}
free(stack);
}
/*
何时访问节点：
当前经过节点是叶子节点
当前经过节点的右子节点是上一次访问的节点
*/
void PostorderTraversal(BinTree BT) {
BinTree* stack = (BinTree*)malloc(sizeof(BinTree) * MAXN);
int top = -1;
BinTree pre;
while (BT || top != -1) {
while (BT) {
stack[++top] = BT;
BT = BT->Left;
}
if (top != -1) {
BT = stack[top--];
if (BT->Right == NULL || pre == BT->Right) {
printf(" %c", BT->Data);
pre = BT; //记录上一次访问的节点
BT = NULL; //跳过下一次循环的访问左子节点的过程
} else {
stack[++top] = BT;
BT = BT->Right;
}
}
}
free(stack);
}
层序遍历：
二叉树遍历的核心：二维结构的序列化，所以我们需要一个存储结构（栈或者队列）保存暂时不访问的节点（父节点）
用队列实现：从根节点开始，首先将根节点入队，然后执行循环：
- 节点出队
- 访问该节点
- 左右儿子入队
代码实现：
//binary-tree-traversal-nr.c
#define MAXN 1001
void LevelorderTraversal(BinTree BT) {
BinTree* queue = (BinTree*)malloc(sizeof(BinTree) * MAXN);
BinTree node;
int front = 0;
int rear = 0;
if (BT) {
queue[++rear] = BT;
}
while (rear != front) {
front = (front + 1) % MAXN, node = queue[front];
printf(" %c", node->Data);
if (node->Left) {
rear = (rear + 1) % MAXN, queue[rear] = node->Left;
}
if (node->Right) {
rear = (rear + 1) % MAXN, queue[rear] = node->Right;
}
}
free(queue);
}
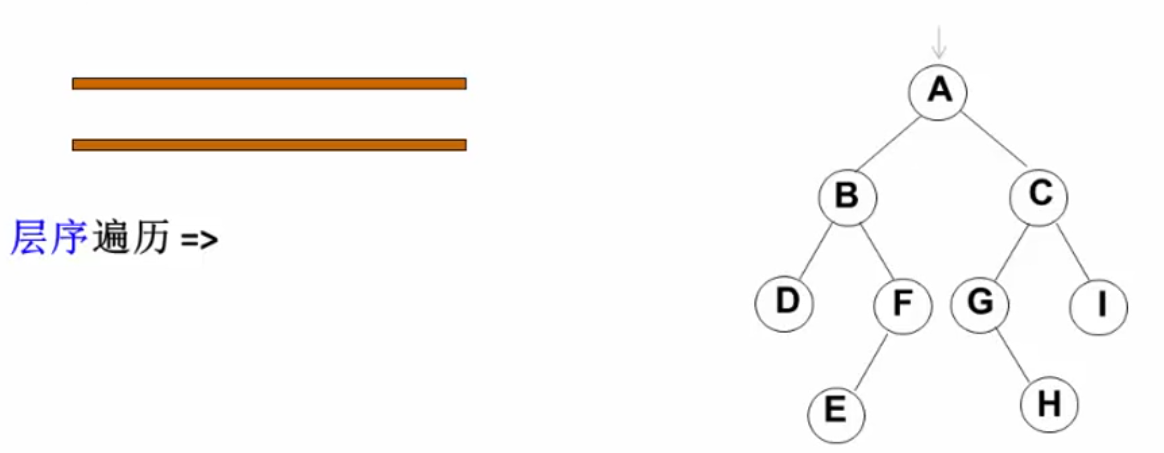
输出序列：ABCDFGIEH
力扣二叉树遍历练习题：
144. 二叉树的前序遍历
94. 二叉树的中序遍历
145. 二叉树的后序遍历
102. 二叉树的层序遍历
遍历应用例子：输出二叉树的叶子节点：在遍历过程的基础上增加判断条件即可
代码实现：
//递归写法
//binary-tree-traversal-r.c
void PreorderPrintLeaves(BinTree BT) {
if (BT != NULL) {
if (BT->Left == NULL && BT->Right == NULL) {
printf(" %c", BT->Data);
}
PreorderPrintLeaves(BT->Left);
PreorderPrintLeaves(BT->Right);
}
}
//非递归写法
//binary-tree-traversal-nr.c
void PreorderPrintLeaves(BinTree BT) {
BinTree* stack = (BinTree*)malloc(sizeof(BinTree) * MAXN);
int top = -1;
while (BT || top != -1) {
while (BT) {
if (BT->Left == NULL && BT->Right == NULL) {
printf(" %c", BT->Data);
}
stack[++top] = BT;
BT = BT->Left;
}
if (top != -1) {
BT = stack[top--];
BT = BT->Right;
}
}
free(stack);
}
求二叉树的高度：本层的高度为左右子树的最大高度加一，递归的进行：
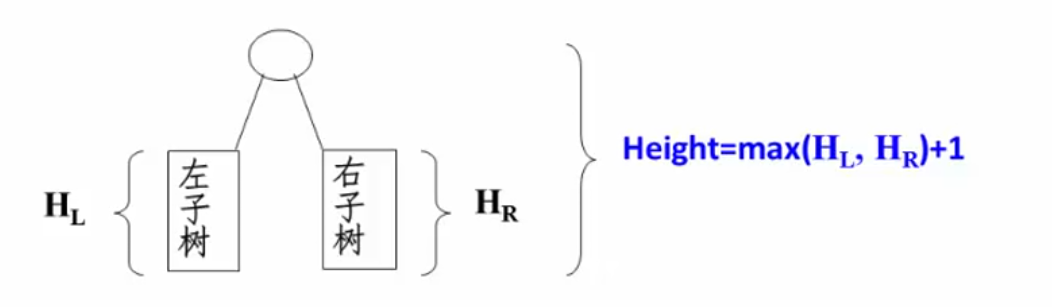
代码实现：
//binary-tree-traversal-r.c
int GetHeight(BinTree BT) {
if (BT) {
int lh = GetHeight(BT->Left);
int rh = GetHeight(BT->Right);
int maxh = lh > rh ? lh : rh;
return maxh + 1;
} else {
return 0;
}
}
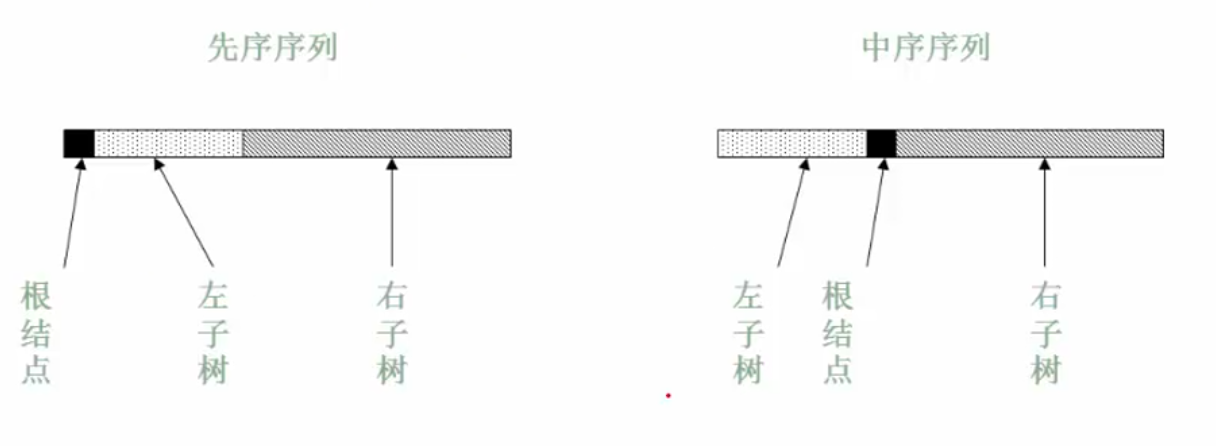
由三种遍历序列中的两种遍历序列还原二叉树：必须要有中序遍历序列
- 根据先序遍历第一个节点确定根节点
- 根据根节点在中序遍历序列中分割出两个子序列
- 对左子树和右子树使用相同的方法继续分解
代码实现：
#include <vector>
#include <stdio.h>
using namespace std;
struct TNode {
TNode(char v, TNode *l, TNode *r) : val(v), left(l), right(r) {}
char val;
TNode *left;
TNode *right;
};
typedef struct TNode *BinTree;
BinTree buildTree(const vector<char> &preorder, const vector<char> &inorder) {
if (inorder.size() == 0) {
return nullptr;
}
char r = preorder[0];
TNode *node = new TNode(r, nullptr, nullptr);
if (preorder.size() == 1) {
return node;
}
int i = 0;
for (; i < inorder.size() && inorder[i] != r; ++i);
vector<char> inorderL(inorder.begin(), inorder.begin() + i);
vector<char> inorderR(inorder.begin() + i + 1, inorder.end());
vector<char> preorderL(preorder.begin() + 1, preorder.begin() + i + 1);
vector<char> preorderR(preorder.begin() + i + 1, preorder.end());
node->left = buildTree(preorderL, inorderL);
node->right = buildTree(preorderR, inorderR);
return node;
}
int getTreeHeight(BinTree T) {
if (T) {
int lh = getTreeHeight(T->left);
int rh = getTreeHeight(T->right);
int maxh = max(lh, rh);
return maxh + 1;
} else {
return 0;
}
}
int main() {
int N;
scanf("%d", &N);
vector<char> preorder;
vector<char> inorder;
getchar();
for (int j = 0; j < N; ++j) {
preorder.push_back(getchar());
}
getchar();
for (int j = 0; j < N; ++j) {
inorder.push_back(getchar());
}
BinTree T = buildTree(preorder, inorder);
printf("%dn", getTreeHeight(T));
return 0;
}
举个例子：先序：abcdefghij，中序：cbedahgijf
力扣上的还原二叉树练习题：
105. 从前序与中序遍历序列构造二叉树
106. 从中序与后序遍历序列构造二叉树
剑指 Offer 07. 重建二叉树
树的同构
题意：
举例子：
输入信息样例：
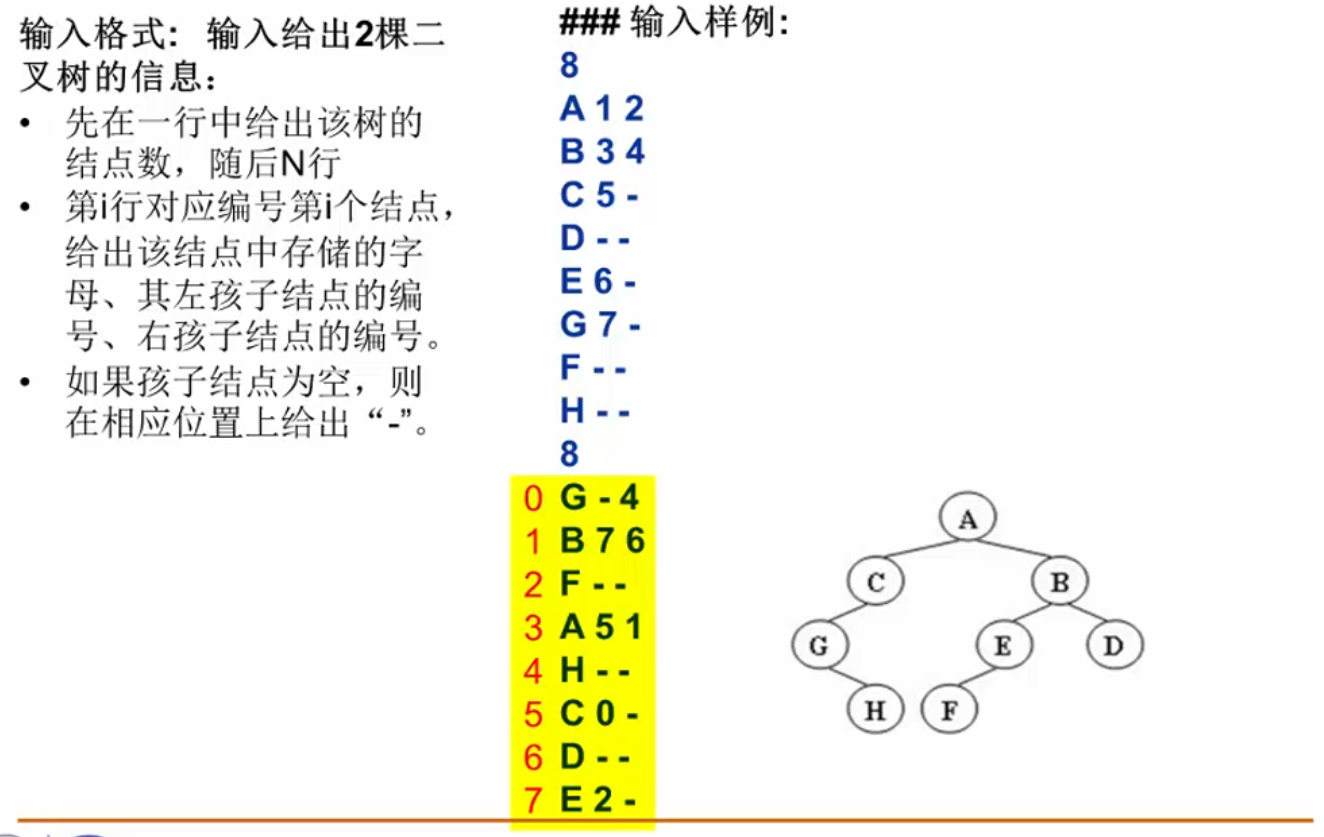
求解思路：
- 二叉树的表示；
- 建立二叉树；
- 同构的判别；
用结构数组表示二叉树：静态链表
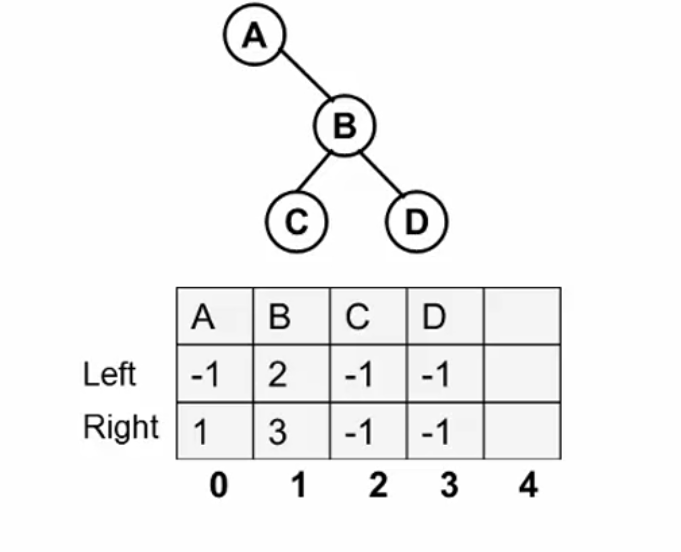
没有被指向的节点就是根节点
程序实现：
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <vector>
#include <algorithm>
#include <list>
#include <stack>
#include <string>
#include <iostream>
#include <queue>
#include <limits.h>
#include <map>
using namespace std;
typedef vector<vector<int>> Mat;
struct TNode {
TNode(char v, char l, char r) : val(v){
if (l != '-') l -= '0';
left = l;
if (r != '-') r -= '0';
right = r;
}
char val;
int left;
int right;
};
bool Isomorphic(vector<TNode>& t1, int root1, vector<TNode>& t2, int root2) {
if (root1 == '-' && root2 == '-') {
return true;
} else if ((root1 == '-' && root2 != '-')|| (root1 != '-' && root2 == '-')) {
return false;
} else if (t1[root1].val != t2[root2].val) {
return false;
} else if (t1[root1].left == '-' && t2[root2].left == '-') {
return Isomorphic(t1, t1[root1].right, t2, t2[root2].right);
} else if (t1[root1].left != '-' && t2[root2].left != '-' && t1[t1[root1].left].val == t2[t2[root2].left].val) {
return Isomorphic(t1, t1[root1].left, t2, t2[root2].left) && Isomorphic(t1, t1[root1].right, t2, t2[root2].right);
} else {
return Isomorphic(t1, t1[root1].left, t2, t2[root2].right) && Isomorphic(t1, t1[root1].right, t2, t2[root2].left);
}
}
int main () {
int N1, N2;
char v, l, r;
vector<TNode> t1, t2;
int root1, root2;
cin >> N1;
vector<int> mark1(N1, 0);
for (int i = 0; i < N1; ++i) {
cin >> v >> l >> r;
t1.push_back(TNode(v, l, r));
if (l != '-') mark1[l - '0']++;
if (r != '-') mark1[r - '0']++;
}
for (int i = 0; i < N1; ++i) {
if (mark1[i] == 0) root1 = i;
}
cin >> N2;
vector<int> mark2(N2, 0);
for (int i = 0; i < N2; ++i) {
cin >> v >> l >> r;
t2.push_back(TNode(v, l, r));
if (l != '-') mark2[l - '0']++;
if (r != '-') mark2[r - '0']++;
}
for (int i = 0; i < N2; ++i) {
if (mark2[i] == 0) root2 = i;
}
if (N1 == 0 && N2 == 0 || Isomorphic(t1, root1, t2, root2)) {
printf("Yesn");
} else {
printf("Non");
}
return 0;
}
一道相同的题：6-7 Isomorphic
二叉搜索树
二叉搜索树，Binary Search Tree，非空左子树的所有键值小于其根节点的键值，非空右子树的根节点的键值大于其根节点的键值，同时左右子树也都是BST
操作函数：
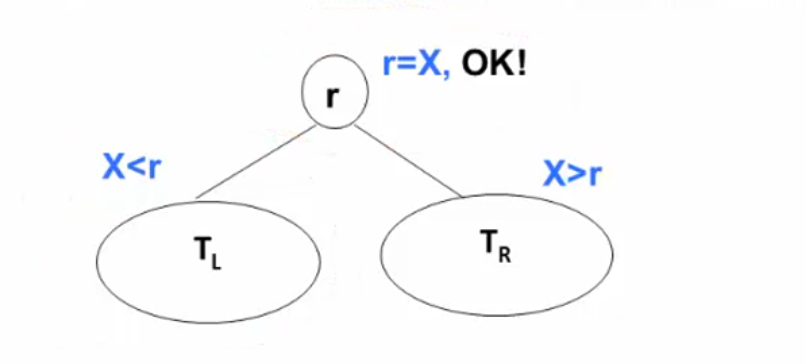
查找从根节点开始，如果树为空，返回NULL
若搜索树非空，则根节点关键字和X进行比较，并进行不同处理：
- 若X小于根节点键值，则进入左子树搜索；
- 若X大于根节点键值，则进入右子树搜索；
- 若X等于根节点键值，搜索完成，返回该节点指针；
//BST.c
//递归查找
Position Find_r(BinTree BST, ElementType X) {
if (BST) {
if (BST->Data == X) {
return BST;
} else if (BST->Data < X) {
return Find_r(BST->Right, X);
} else {
return Find_r(BST->Left, X);
}
}
return BST;
}
//从编译角度来讲，尾递归都是可以优化为循环的：
Position Find_nr(BinTree BST, ElementType X) {
while (BST) {
if (BST->Data == X) {
return BST;
} else if (X > BST->Data) {
BST = BST->Right;
} else {
BST = BST->Left;
}
}
return BST;
}
Position Find(BinTree BST, ElementType X) {
int r = rand(); //随机使用查找算法
return (r & 1) ? Find_r(BST, X) : Find_nr(BST, X);
}
查找效率取决于树的高度： O ( N ) = l o g N = h O(N) = logN=h O(N)=logN=h
递归的查找最大节点：
//BST.c
Position FindMax(BinTree BST) {
if (BST == NULL) {
return NULL;
} else if (BST->Right == NULL) {
return BST;
} else {
return FindMax(BST->Right);
}
}
迭代的查找最小节点：
//BST.c
Position FindMin(BinTree BST) {
while (BST && BST->Left) {
BST = BST->Left;
}
return BST;
}
二叉搜索树的插入：
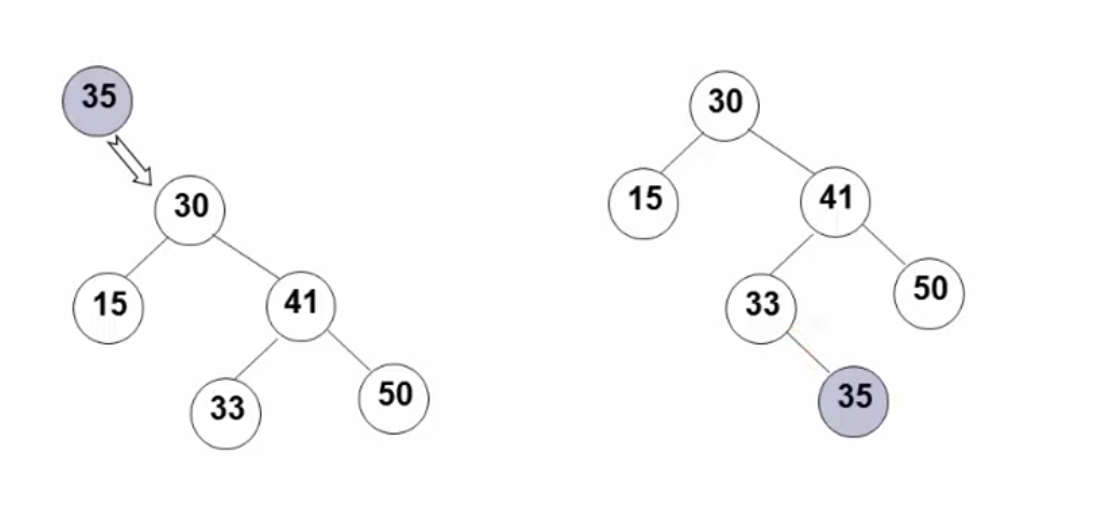
代码实现：
//BST.c
BinTree Insert(BinTree BST, ElementType X) {
if (BST == NULL) {
BST = (BinTree)malloc(sizeof(struct TNode));
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
} else if (X > BST->Data) {
BST->Right = Insert(BST->Right, X);
} else if (X < BST->Data) {
BST->Left = Insert(BST->Left, X);
}
return BST;
}
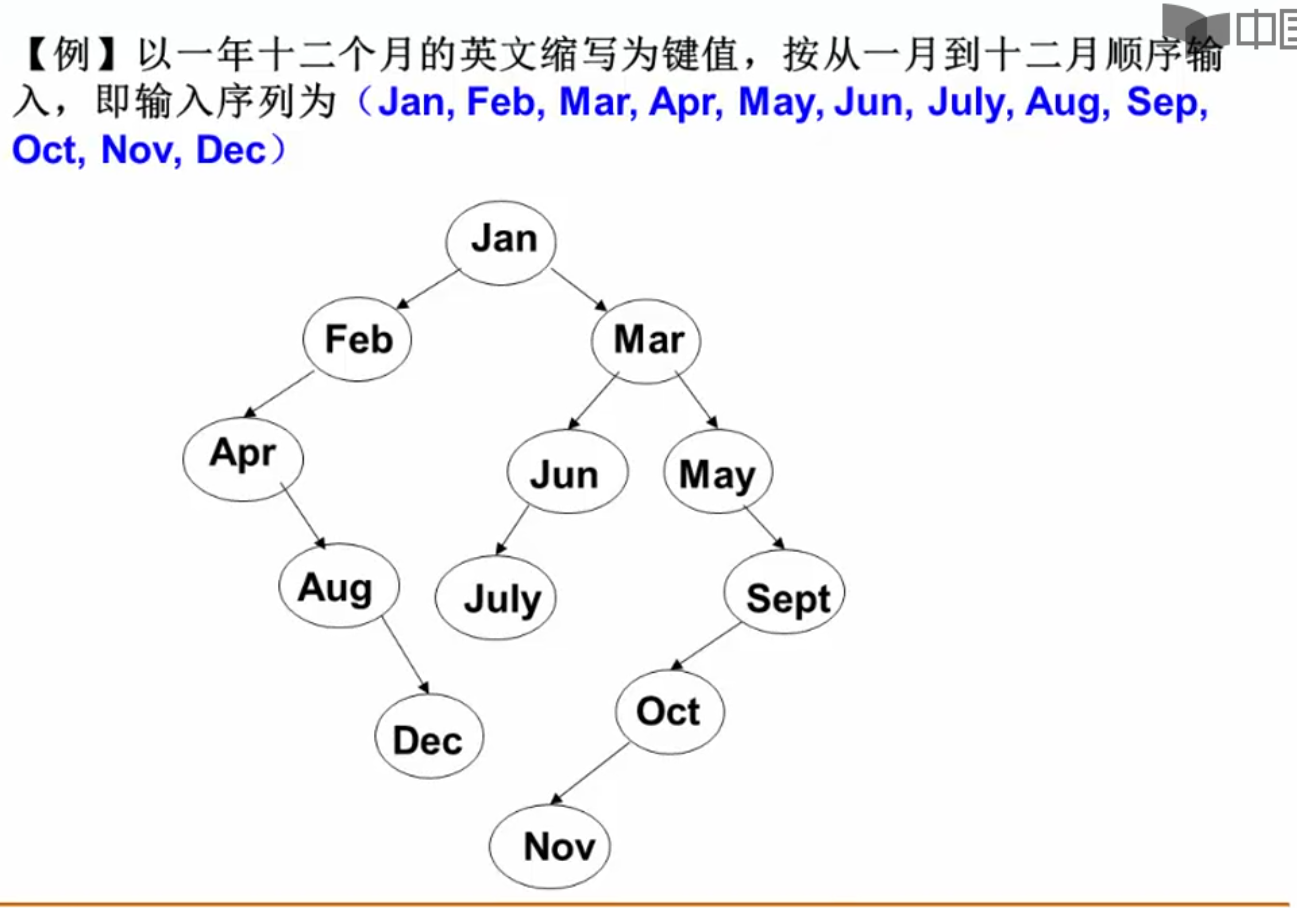
按照字典序插入的一个例子：
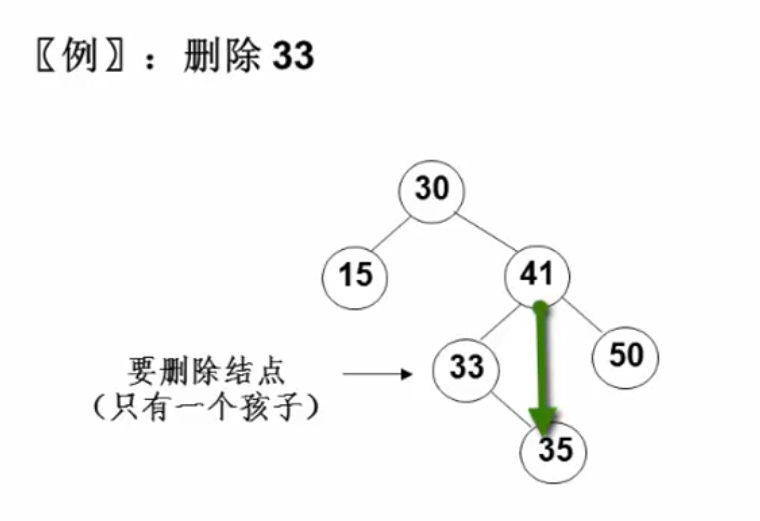
二叉搜索树的删除，要考虑三种情况：
-
要删除的是叶节点：直接删除，并修改其父节点指针=NULL
-
要删除的节点只有一个孩子节点：将其父节点的指针指向要删除节点的孩子节点：
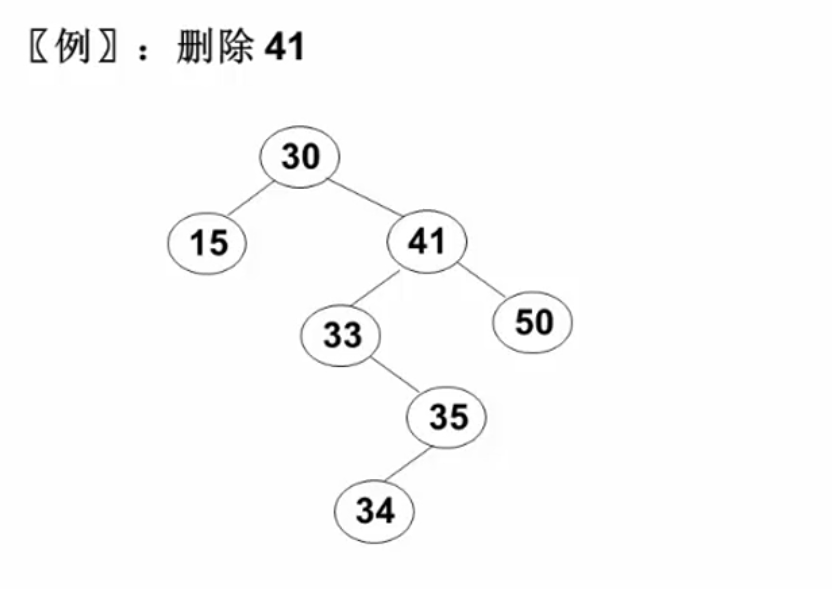
- 要删除的节点有左右两棵子树：用另一节点代替被删除的节点：右子树的最小元素或左子树的最大元素：
两种删除策略：
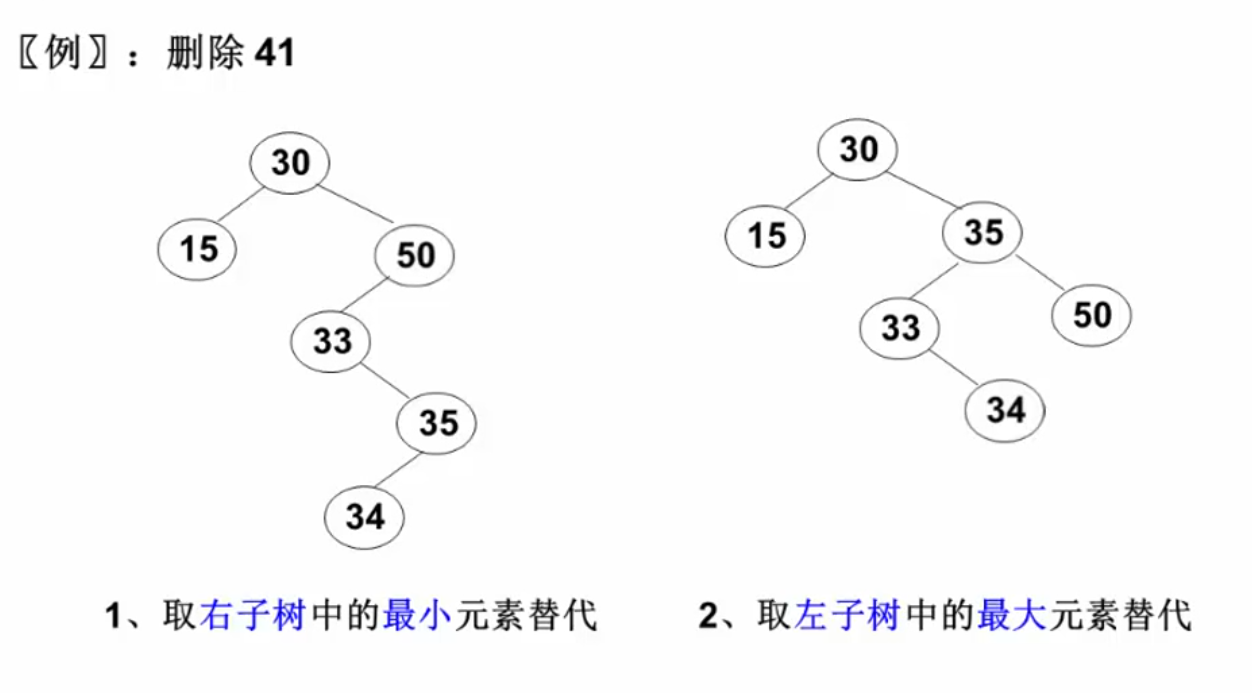
右子树的最小值一定在右子树的最左边，没有左儿子；左子树的最大值一定在左子树的最右边，没有右儿子
BinTree Delete(BinTree BST, ElementType X) {
BinTree t = NULL;
if (BST == NULL) {
printf("Not Foundn");
} else if (X > BST->Data) {
BST->Right = Delete(BST->Right, X);
} else if (X < BST->Data) {
BST->Left = Delete(BST->Left, X);
} else {
if (BST->Left && BST->Right) {
t = FindMin(BST->Right);
BST->Data = t->Data;
BST->Right = Delete(BST->Right, t->Data);
} else {
if (BST->Left == NULL) {
BST = BST->Right;
} else if (BST->Right == NULL) {
BST = BST->Left;
}
}
free(t);
}
return BST;
}
平衡二叉树
搜索树节点不同的插入顺序，将导致不同的深度和平均查找长度ASL
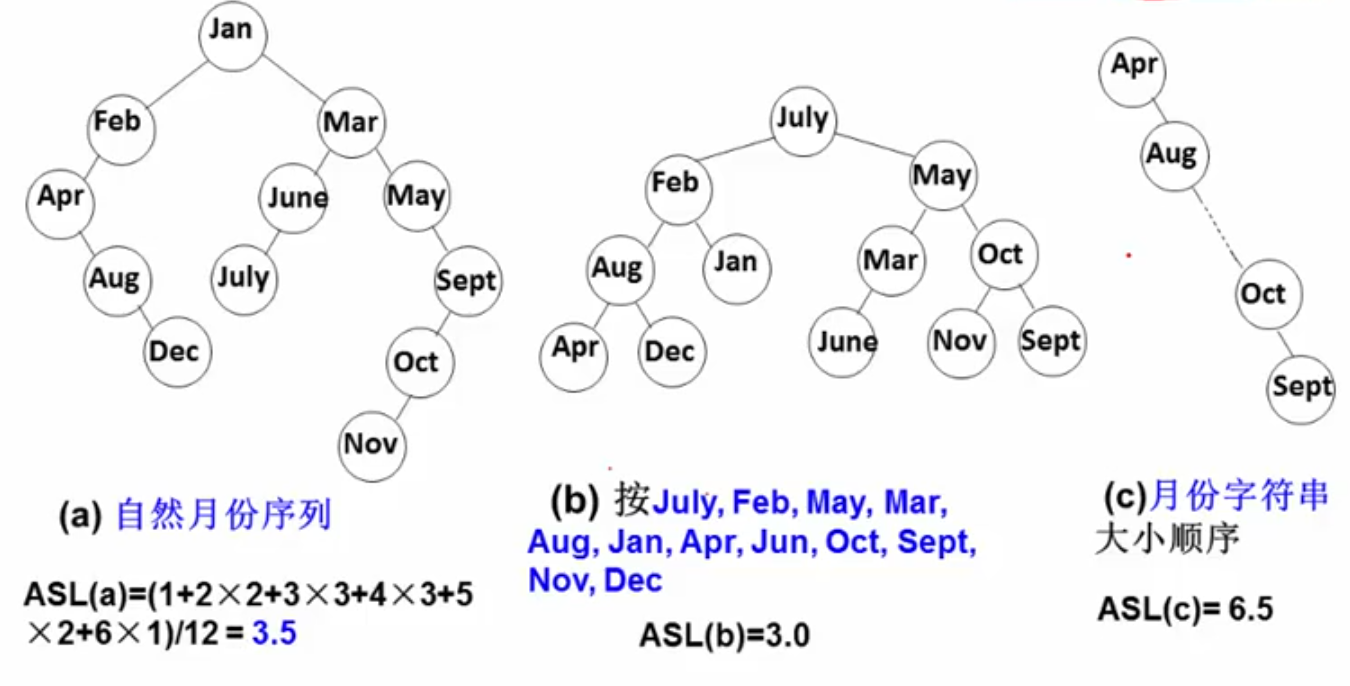
AVL树：
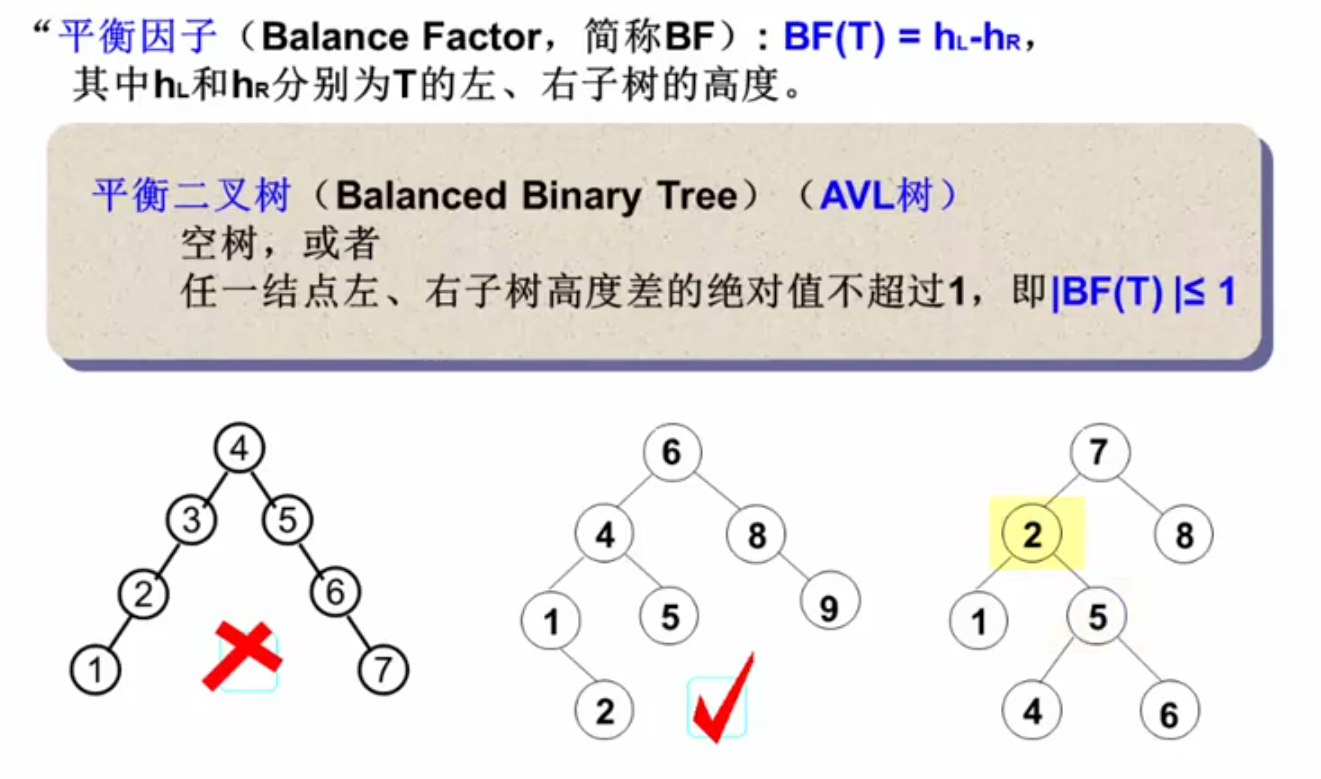
在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。
树的高度：
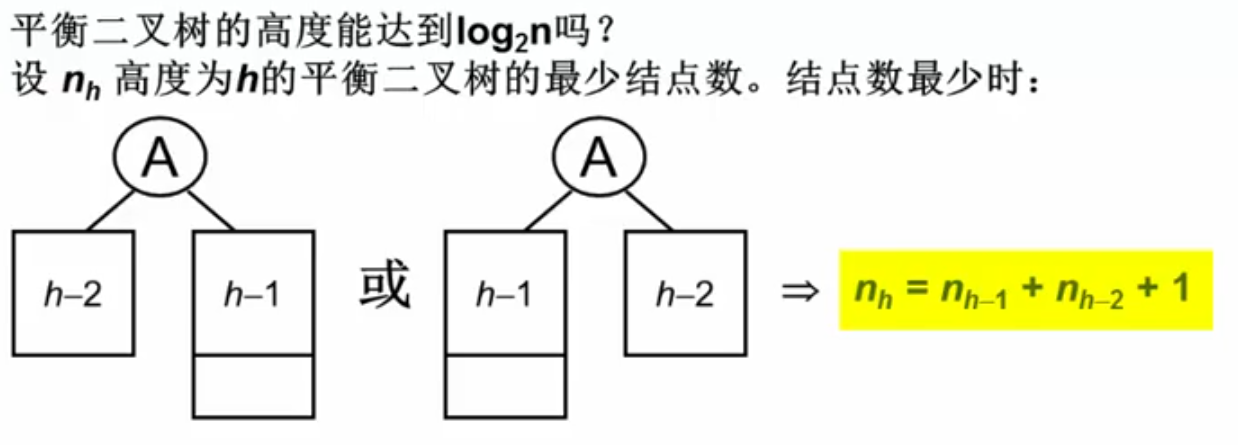
高度的递推公式为斐波那契数列：
F 0 = 1 , F 1 = 1 , F i = F i − 1 + F i − 2 , f o r i > 1 F_0 = 1, F_1 = 1, F_i = F_{i-1} + F_{i-2}, for i > 1 F0=1,F1=1,Fi=Fi−1+Fi−2, for i>1
查找效率推导：
观察表格得：
n
h
=
F
h
+
2
−
2
n_h=F_{h+2}-2
nh=Fh+2−2
由斐波那契数列的近似形式：
F
i
≈
1
5
(
1
+
5
2
)
i
F_i≈frac{1}{sqrt{5}}(frac{1+sqrt{5}}{2})^i
Fi≈51(21+5)i
从而：
n
h
≈
1
5
(
1
+
5
2
)
h
+
2
−
1
n_h≈frac{1}{sqrt{5}}(frac{1+sqrt{5}}{2})^{h+2}-1
nh≈51(21+5)h+2−1
从而：
h
=
O
(
log
n
)
h=O(log{n})
h=O(logn)
给定节点树为n的AVL树的最大高度为O(logn)
判断一棵BST是否为一棵AVLTree：
bool isBalanced(TreeNode* root) {
return height(root) >= 0;
}
int height(TreeNode* root) {
if(root == nullptr) {
return 0;
}
int lh = height(root->left);
int rh = height(root->right);
if (lh >= 0 && rh >= 0 && abs(lh - rh) <= 1) {
return max(lh, rh) + 1;
} else {
return -1;
}
}
平衡二叉树的调整：
RR右单旋：
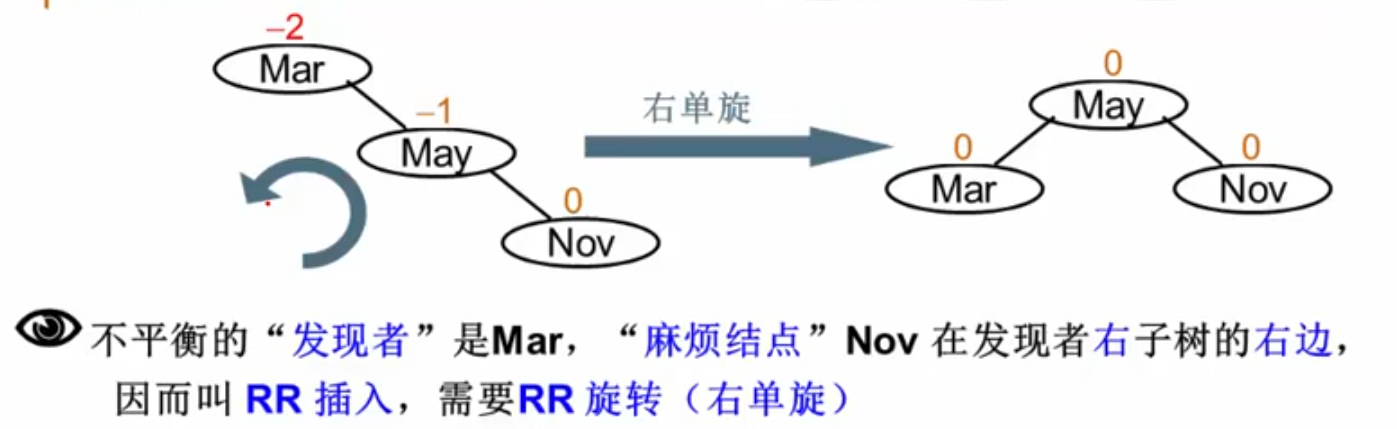
麻烦节点在发现者右子树的右边，做RR旋转：将右儿子拎上去，自己下来，将BL挂在右子树：
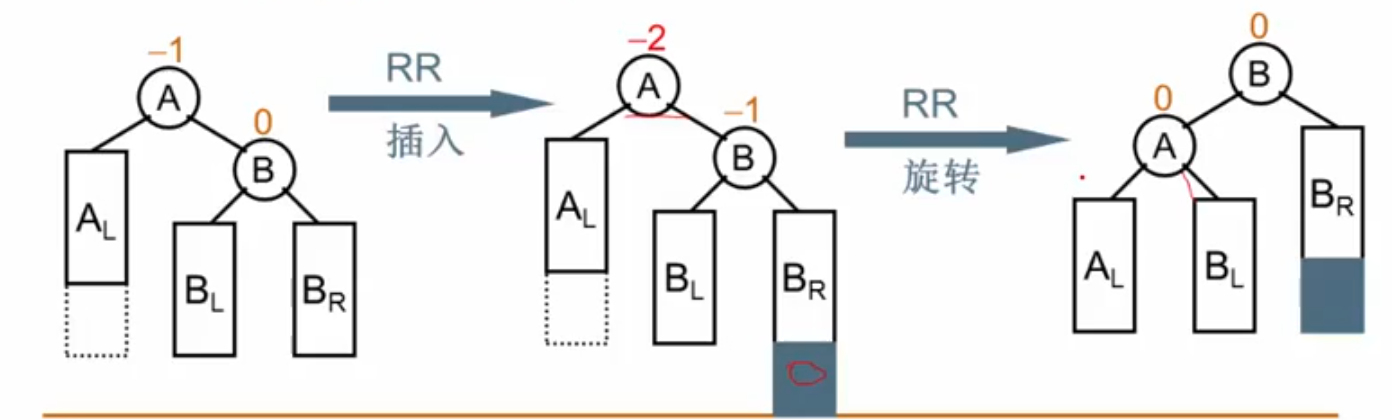
例子：
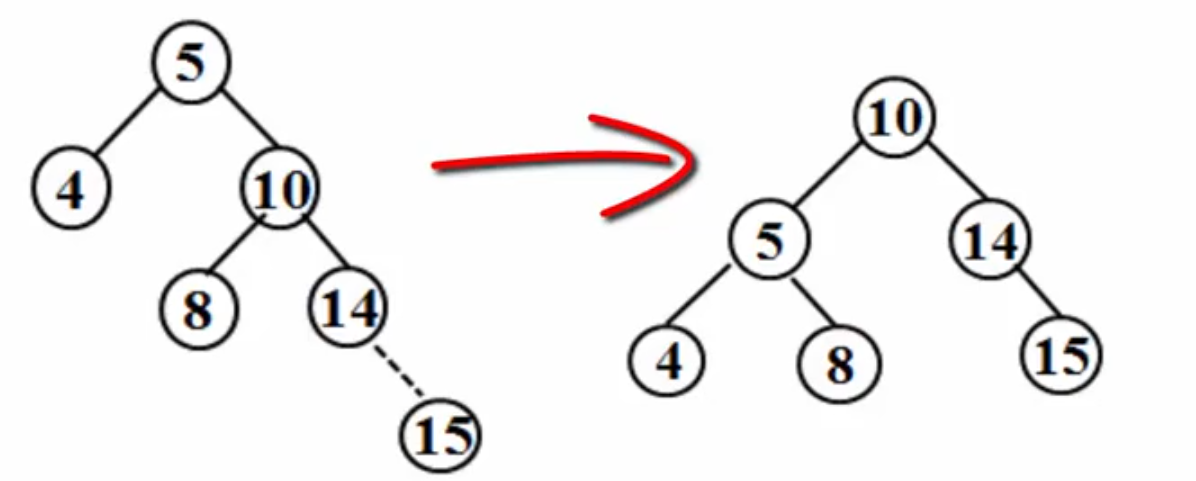
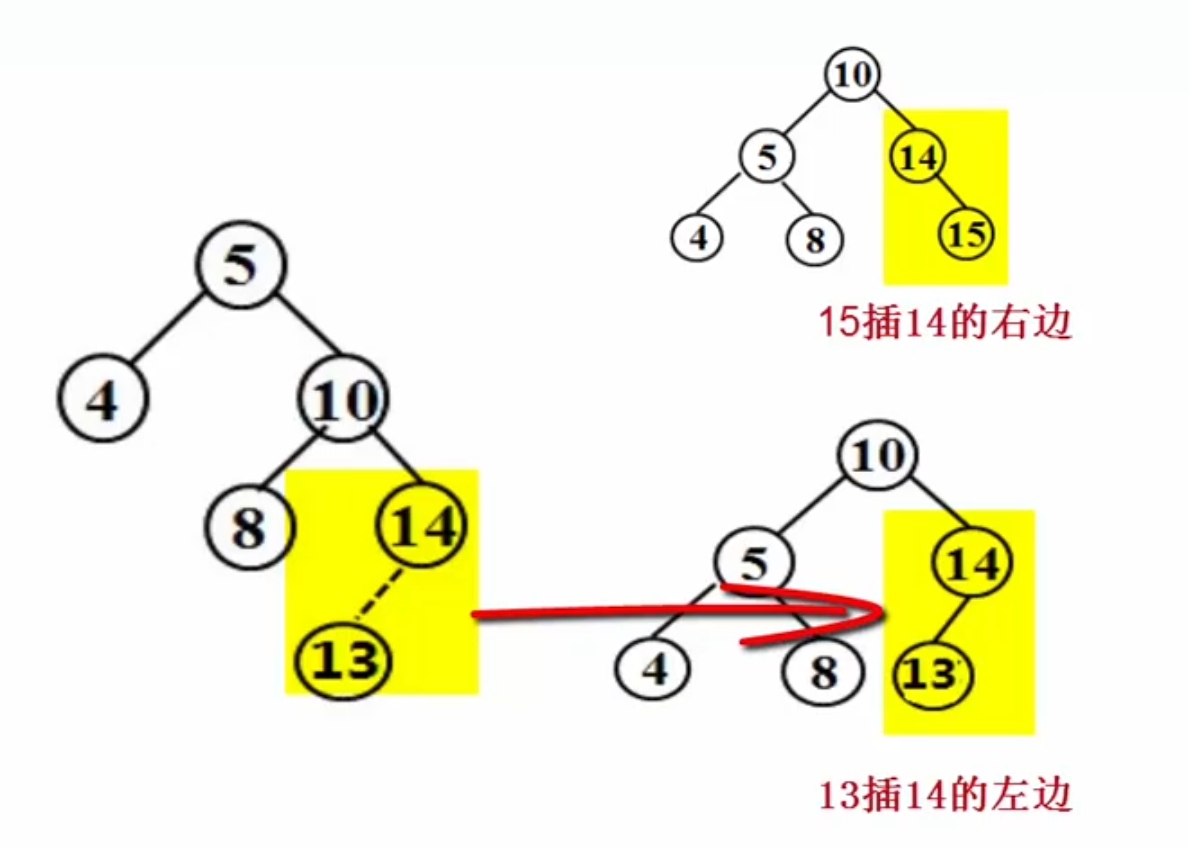
LL左单旋：
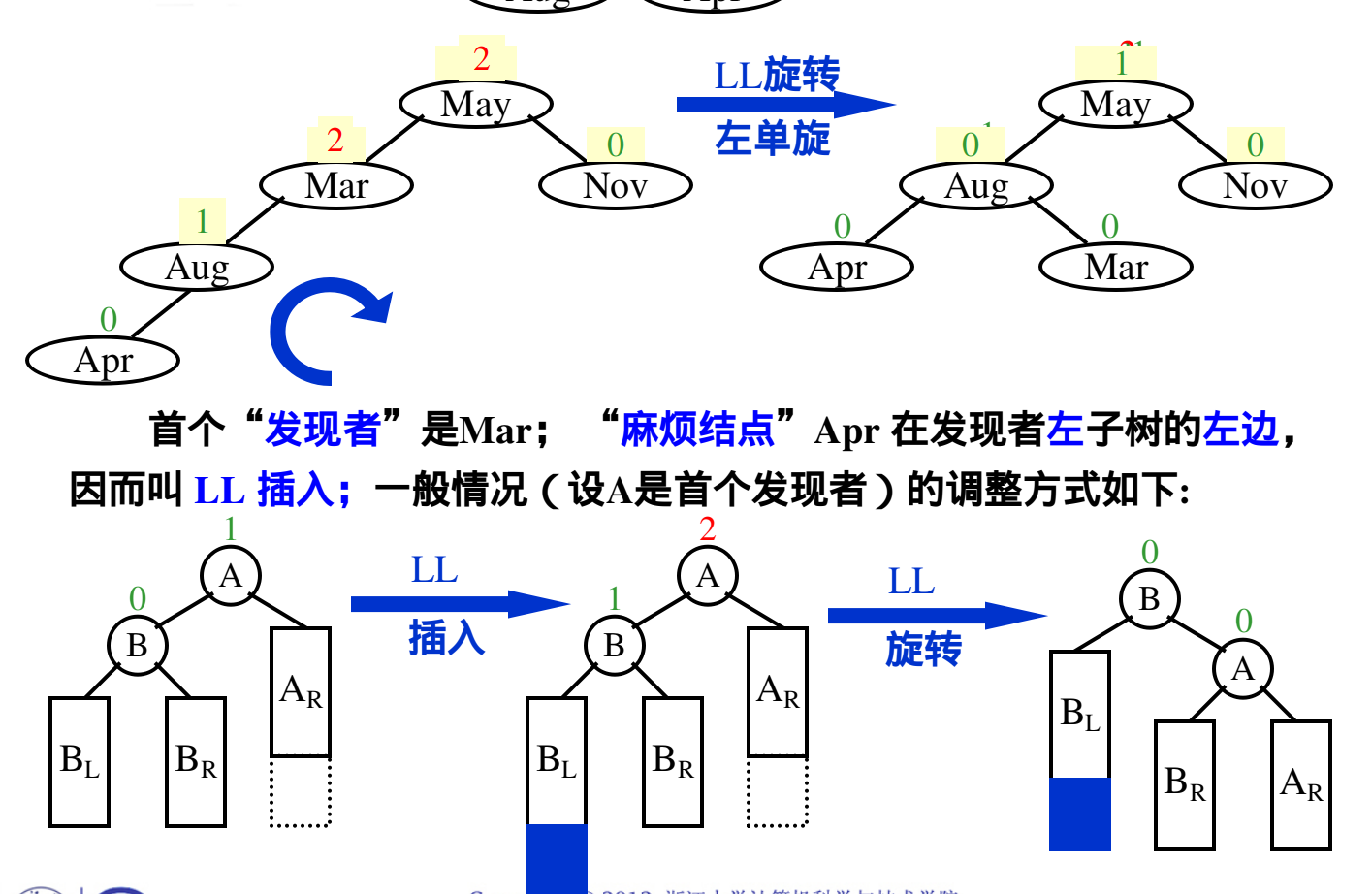
LR左右旋转：
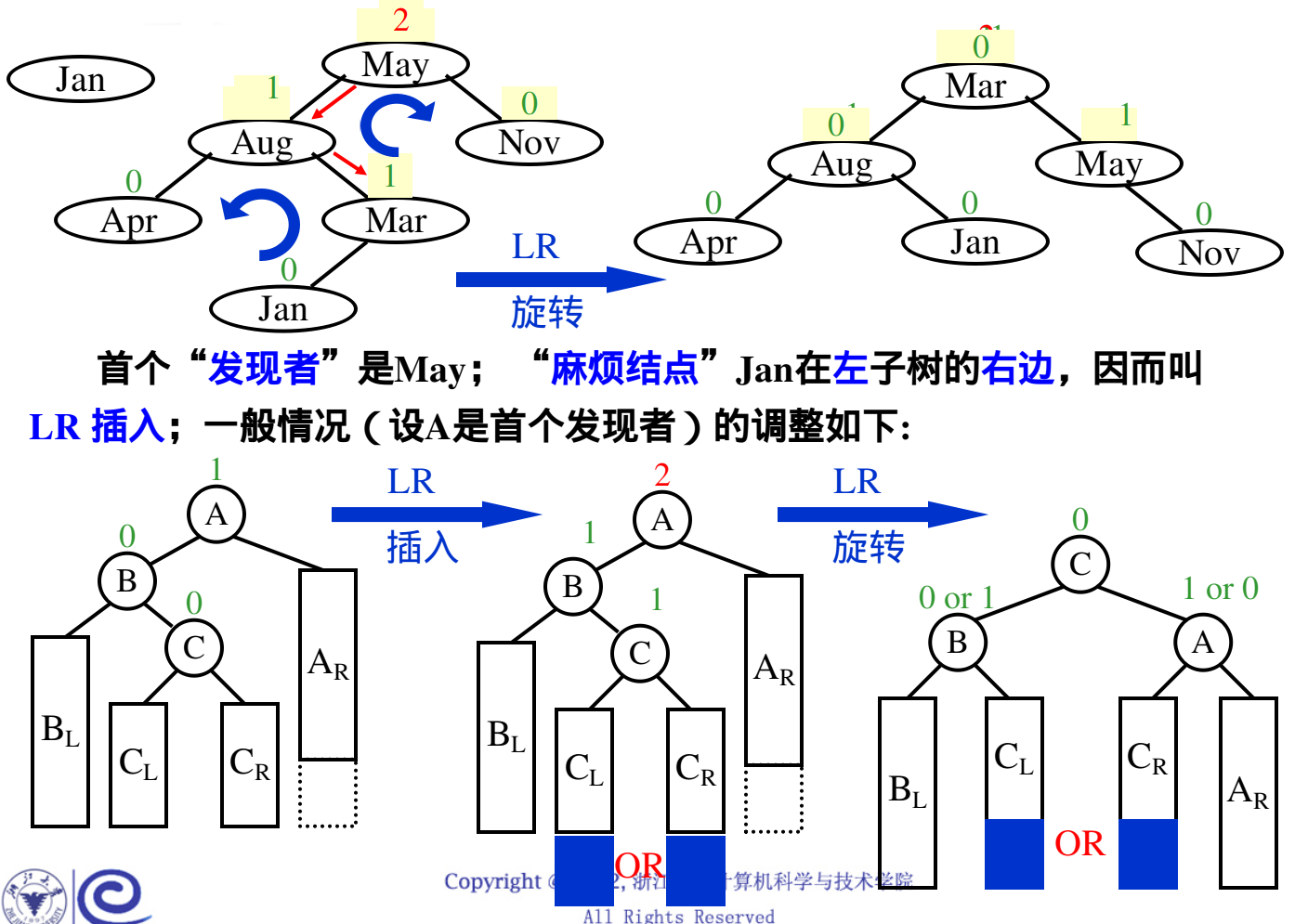
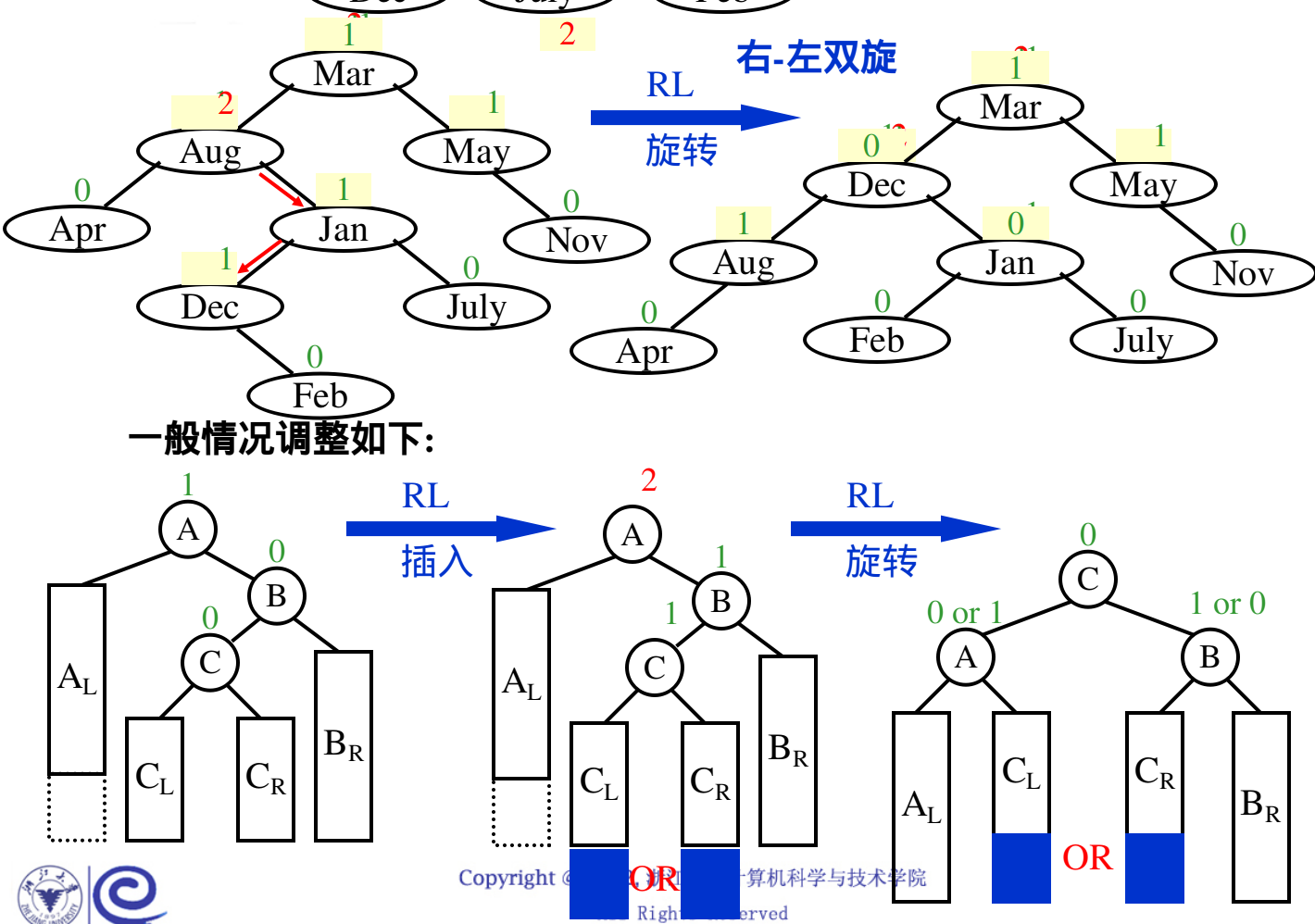
RL右左旋转：
算法实现：
//AVLTree.c
#include <stdio.h>
#include <stdlib.h>
#define AVLTreeElemType int
struct AVLNode {
AVLTreeElemType data;
struct AVLNode* left;
struct AVLNode* right;
int height;
};
typedef struct AVLNode* AVLTree;
int max(int a, int b) {
return (a > b) ? a : b;
}
int AVLTreeHeight(AVLTree t) {
if (t == NULL)
return 0;
else
return t->height;
}
//LL
AVLTree SingleLeftRotation(AVLTree A) {
AVLTree B = A->left;
A->left = B->right;
B->right = A;
A->height = max(AVLTreeHeight(A->left), AVLTreeHeight(A->right)) + 1;
B->height = max(AVLTreeHeight(B->left), AVLTreeHeight(B->right)) + 1;
return B;
}
//RR
AVLTree SingleRightRotation(AVLTree A) {
AVLTree B = A->right;
A->right = B->left;
B->left = A;
A->height = max(AVLTreeHeight(A->left), AVLTreeHeight(A->right)) + 1;
B->height = max(AVLTreeHeight(B->left), AVLTreeHeight(B->right)) + 1;
return B;
}
//LR
AVLTree DoubleLeftRightRotation(AVLTree A) {
//先对左子树RR旋转
A->left = SingleRightRotation(A->left);
//再对A做LL旋转
return SingleLeftRotation(A);
}
//RL
AVLTree DoubleRightLeftRotation(AVLTree A) {
A->right = SingleLeftRotation(A->left);
return SingleRightRotation(A);
}
AVLTree AVLTreeInsert(AVLTree t, AVLTreeElemType x) {
if (t == NULL) {
t = (AVLTree)malloc(sizeof(struct AVLNode));
t->data = x;
t->height = 1;
t->left = t->right = NULL;
} else if (x < t->data) {
t->left = AVLTreeInsert(t->left, x);
if (AVLTreeHeight(t->left) - AVLTreeHeight(t->right) == 2) {
if (x < t->left->data) {
t = SingleLeftRotation(t);
} else {
t = DoubleLeftRightRotation(t);
}
}
} else if (x > t->data) {
t->right = AVLTreeInsert(t->right, x);
if (AVLTreeHeight(t->left) - AVLTreeHeight(t->right) == -2) {
if (x > t->right->data) {
t = SingleRightRotation(t);
} else {
t = DoubleRightLeftRotation(t);
}
}
} //else x==t->data，无需插入
t->height = max(AVLTreeHeight(t->left), AVLTreeHeight(t->right)) + 1;
return t;
}
是否同一棵二叉搜索树
题意理解：
求解思路：
法1：分别建两课BST，然后判别这两棵树是不是一样：先判断根，然后递归的判断左子树和右子树。
法2：不建树，利用根节点将序列划分为左右两棵子树，然后同样递归的判断左右子树是否一样。
法3：建一棵树，再判别其他序列是否与该树一致：如果到某节点的路径上出现了以前未访问过的节点，则false。
下面采用法3。
树节点定义，增加一个是否访问过的域visited：
//is-the-same-bst.cpp
typedef struct TreeNode* BinTree;
struct TreeNode {
TreeNode (int n, BinTree l, BinTree r, int v) : val(n), left(l), right(r), visited(v) {}
int val;
TreeNode* left;
TreeNode* right;
int visited;
};
程序框架：
//is-the-same-bst.cpp
int main() {
int N, L, n;
scanf("%d", &N);
while (N) {
scanf("%d", &L);
scanf("%d", &n);
TreeNode* root = new TreeNode(n, nullptr, nullptr, 0);
for (int i = 1; i < N; ++i) {
scanf("%d", &n);
root = Insert(root,n);
}
for (int i = 0; i < L; ++i) {
bool flag = true;
for (int j = 0; j < N; ++j) {
scanf("%d", &n);
if (!Judge(root, n)) {
flag = false;
}
}
if (flag) {
printf("Yesn");
} else {
printf("Non");
}
resetTree(root);
}
deleteTree(root);
scanf("%d", &N);
}
return 0;
}
递归的判别插入：
//is-the-same-bst.cpp
BinTree Insert(BinTree bt, int val){
if (bt == nullptr) {
return new TreeNode(val, nullptr, nullptr, 0);
}
if (val < bt->val) {
bt->left = Insert(bt->left, val);
} else if (val > bt->val) {
bt->right = Insert(bt->right, val);
}
return bt;
}
如何判别：
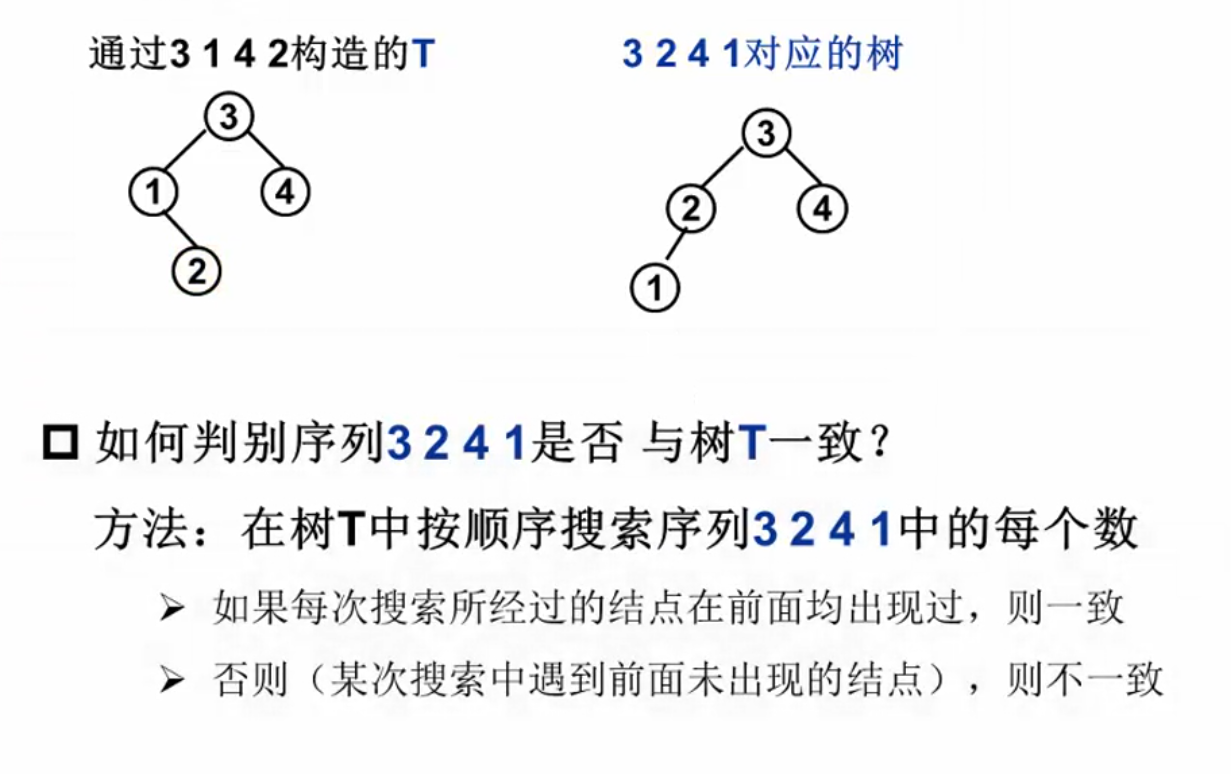
判别：
//is-the-same-bst.cpp
bool Judge(BinTree bt, int n) {
if (bt==nullptr || (bt->visited == false && bt->val != n)) {
return false;
}
if (bt->val == n && bt->visited == false) {
bt->visited = true;
return true;
} else if (bt->val < n) {
return Judge(bt->right, n);
} else {
return Judge(bt->left, n);
}
}
节点恢复和释放内存：
//is-the-same-bst.cpp
void resetTree(BinTree bt) {
if (bt) {
bt->visited = 0;
resetTree(bt->left);
resetTree(bt->right);
}
}
void deleteTree(BinTree bt) {
if (bt->left) {
deleteTree(bt->left);
}
if (bt->right) {
deleteTree(bt->right);
}
delete bt;
}
堆
优先队列（Priority Queue）：特殊的队列，取出元素的顺序是按照元素的优先权（关键字）的大小，而不是元素进入队列的先后顺序
可以采用完全二叉树实现，令根节点大于左右孩子节点
若采用线性结构实现：
堆用完全二叉树进行存储（用数组表示），每个节点都是其子树所有节点的最大值
堆的特性：
- 结构性：用数组表示的完全二叉树；
- 有序性：任意节点的关键字是其子树所有节点的最大值或最小值，分别对应大顶堆和小顶堆；
优先队列的完全二叉树表示：
两个最大堆和最小堆：
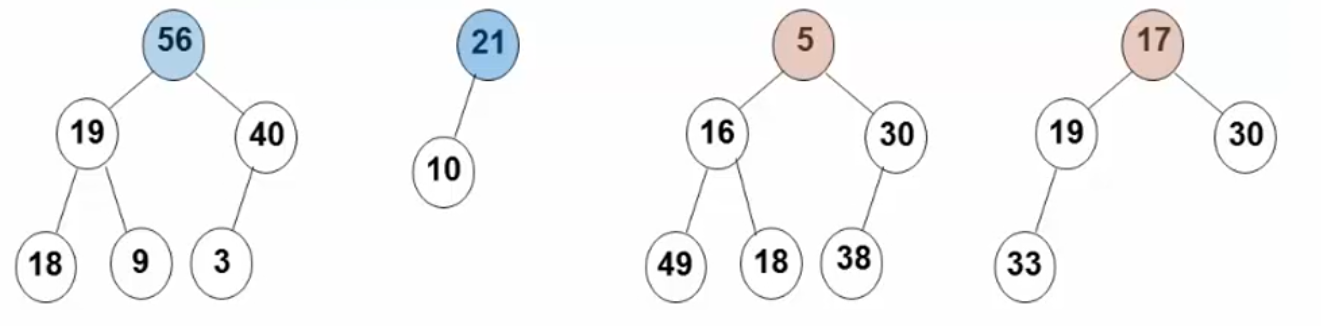
从根节点到任意节点路径上节点序列的有序性；
堆的抽象数据类型描述：
堆的结构定义：
//heap.c
//哨兵值
#define MAXDATA INT_MAX
#define MINDATA INT_MIN
typedef int HeapElemType;
struct HeapNode {
HeapElemType* data;
int size;
int capacity;
};
typedef struct HeapNode* MaxHeap;
typedef struct HeapNode* MinHeap;
堆的创建与销毁函数：
//heap.c
MaxHeap CreateMaxHeap(int MaxSize) {
MaxHeap H = (MaxHeap)malloc(sizeof(struct HeapNode));
//为数组开空间，0号元素存的是哨兵，所以要+1
H->data = (HeapElemType*)malloc((MaxSize + 1) * sizeof(struct HeapNode));
H->size = 0;
H->capacity = MaxSize;
//哨兵
H->data[0] = MAXDATA;
return H;
}
void DestoryHeap(struct HeapNode* h) {
if (h != NULL) {
if (h->data != NULL)
free(h->data);
free(h);
}
}
堆的插入过程：
直接插在最后，如下，插入20，不破坏堆的结构的有序性：
但是插入的数据比其父节点大时，需要调整位置：
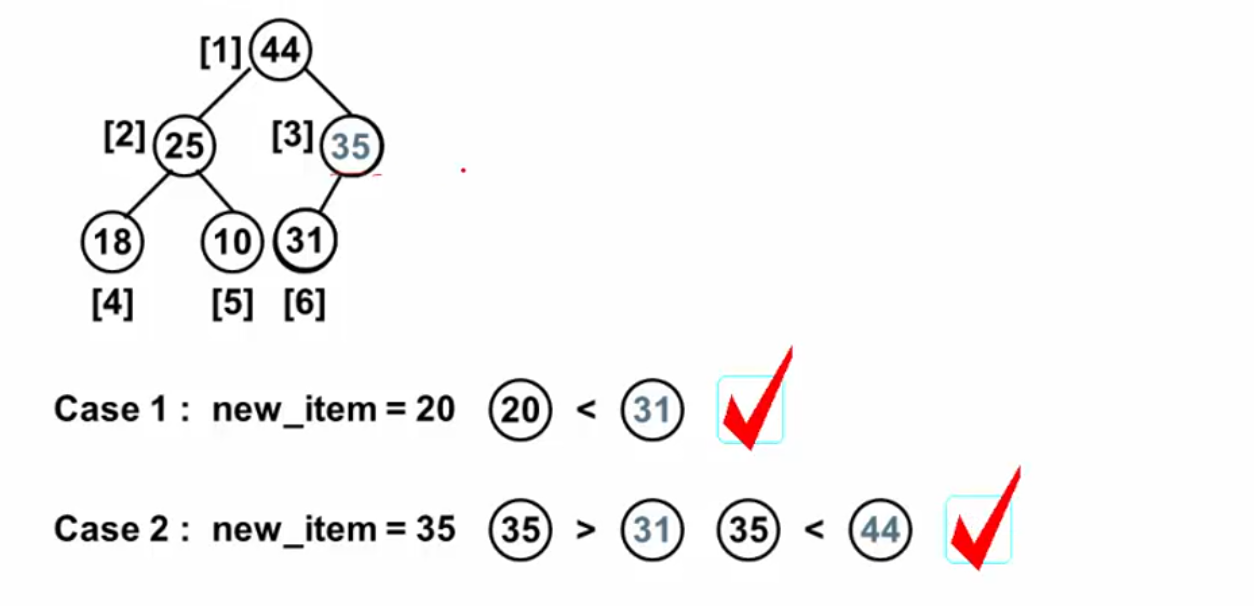
插入过程的代码实现：
//heap.c
bool InsertMaxHeap(MaxHeap H, HeapElemType item) {
if (isHeapFull(H)) {
return false;
}
//刚开始假设插入的位置在数组的最后
int i = ++H->size;
//只要item比父节点大：
while (item > H->data[i / 2]) {
//父节点下来
H->data[i] = H->data[i / 2];
//我上去
i = i / 2;
}
//跳出循环时i锚定了合适的插入位置，赋值
H->data[i] = item;
return true;
}
堆的删除：根据堆的定义，应该删除根节点，但是删除后堆少了一个元素，需要用最后一个元素替补根节点的位置，这样就需要我们进行调整，使之满足堆的特性
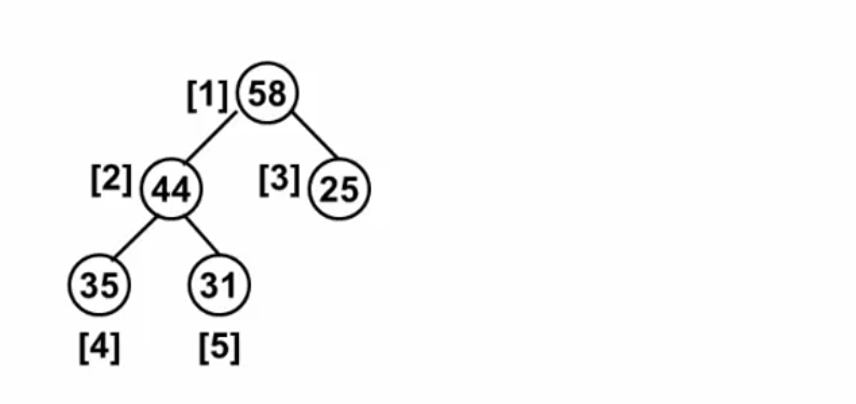
删除过程：
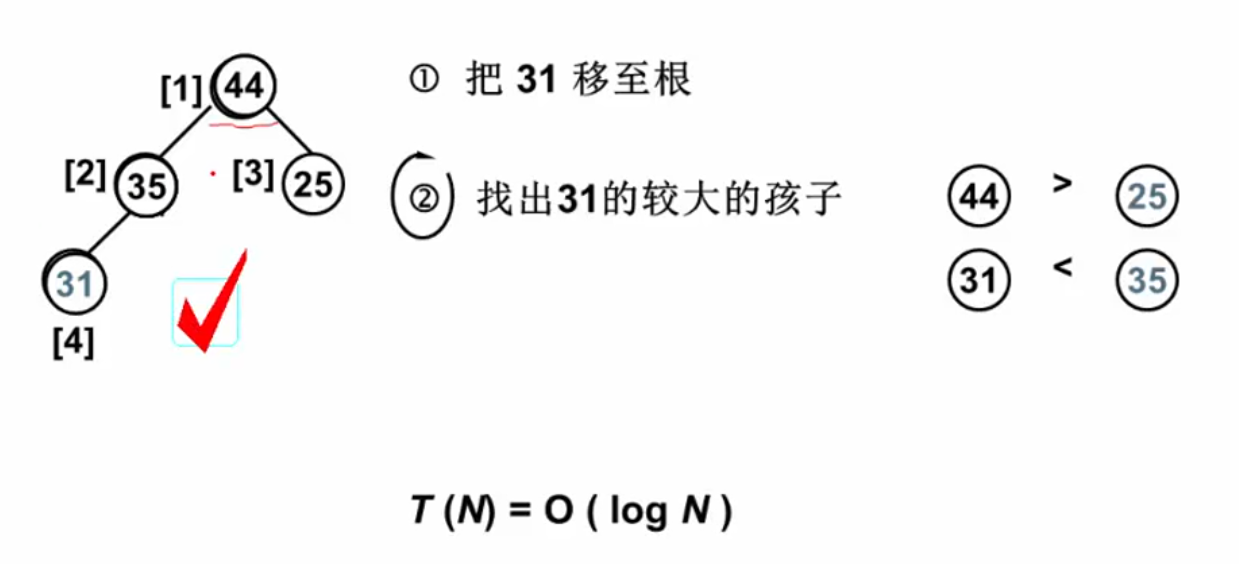
算法实现：
//heap.c
HeapElemType DeleteMax(MaxHeap H) {
if (isHeapEmpty(H)) {
return H->data[0];
}
HeapElemType MaxItem = H->data[1];
HeapElemType tmp = H->data[H->size--];
int Parent = 1;
int Child;
//算法核心：给tmp找到合适的位置
while (Parent * 2 <= H->size) {
// Child指向左孩子
Child = 2 * Parent;
// Child指向左右孩子中最大者
if ((Child != H->size) && H->data[Child] < H->data[Child + 1]) {
Child++;
}
//如果tmp>左右孩子最大者，说明tmp在这里坐得住，跳出循环
if (tmp > H->data[Child]) {
break;
} else {
//让孩子上来
H->data[Parent] = H->data[Child];
//自己下去
Parent = Child;
}
}
H->data[Parent] = tmp;
return MaxItem;
}
堆的一个重要应用是堆排序，这需要我们将一个无序数组建立为堆
建立最大堆：将已经存在的N各个元素按照最大堆的要求存放在一个一维数组中
在O(N)的时间内建堆：
- 将N个元素按照输入顺序存入一个完全二叉树；
- 调整各节点的位置，使之有序；
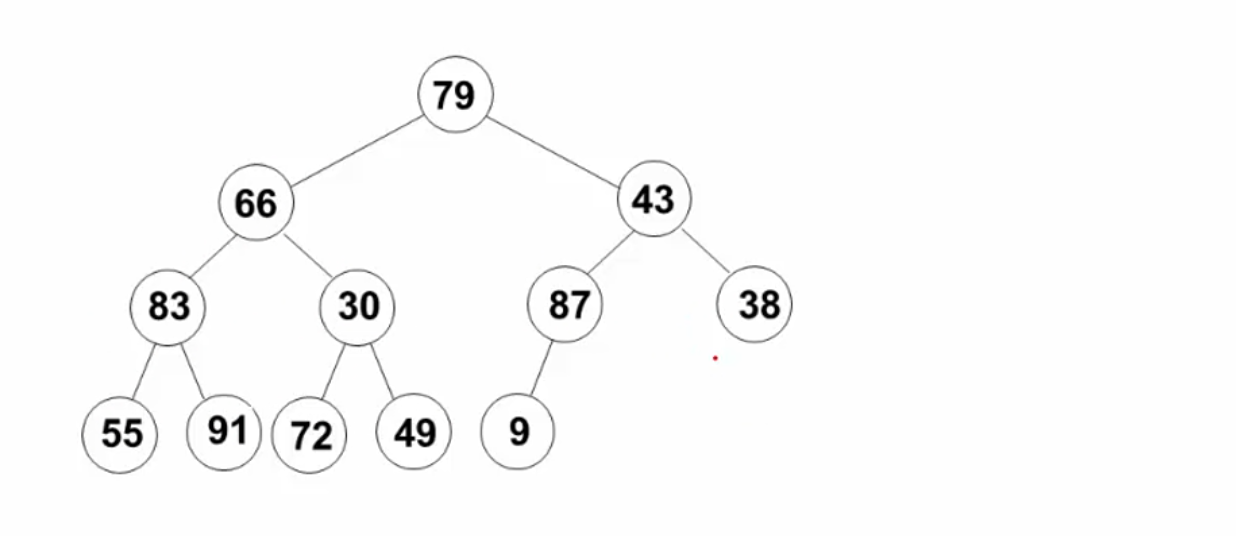
策略：从底下倒数第一个有儿子的节点开始，依次向前迭代建堆；
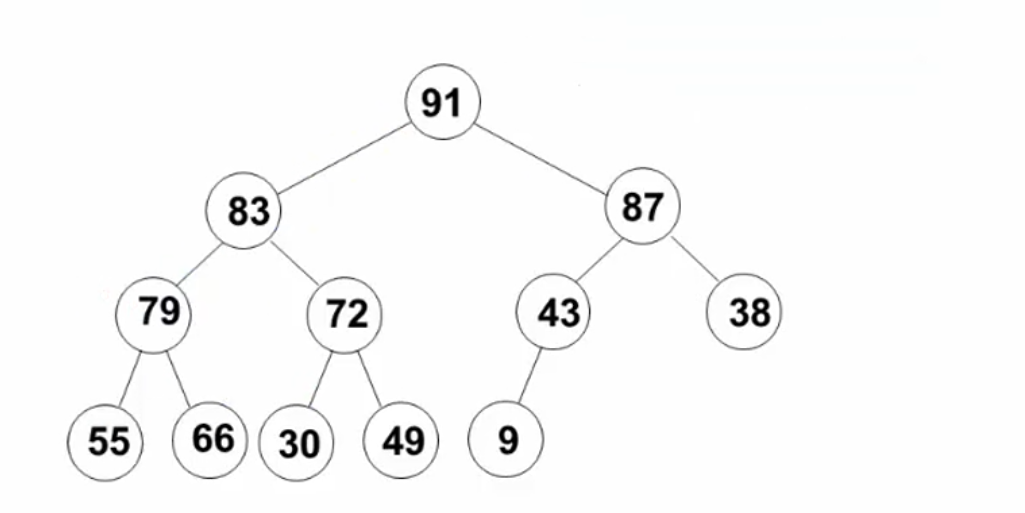
堆的建立实现：
//heap.c
void percDownMaxHeap(MaxHeap H, int n) {
HeapElemType top;
int Child;
int Parent = n;
top = H->data[n];
//向下过滤
for (Parent = n; Parent * 2 <= H->size; Parent = Child) {
Child = 2 * Parent;
if (Child != H->size && H->data[Child] < H->data[Child + 1]) {
Child++;
}
if (top >= H->data[Child]) {
break;
} else {
H->data[Parent] = H->data[Child];
}
}
H->data[Parent] = top;
}
void initMaxHeap(struct HeapNode* H) {
//从最后一个有儿子的节点开始
for (int i = (H->size / 2); i > 0; i--) {
percDownMaxHeap(H, i);
}
}
哈夫曼树与哈夫曼编码
如果大部分人都是90+，则根据判定树，会浪费很多判断过程，其查找效率为：
考虑分数的概率分布，优化搜索树：
启示：根据节点的查找效率构造不同的搜索树
哈夫曼树的定义：
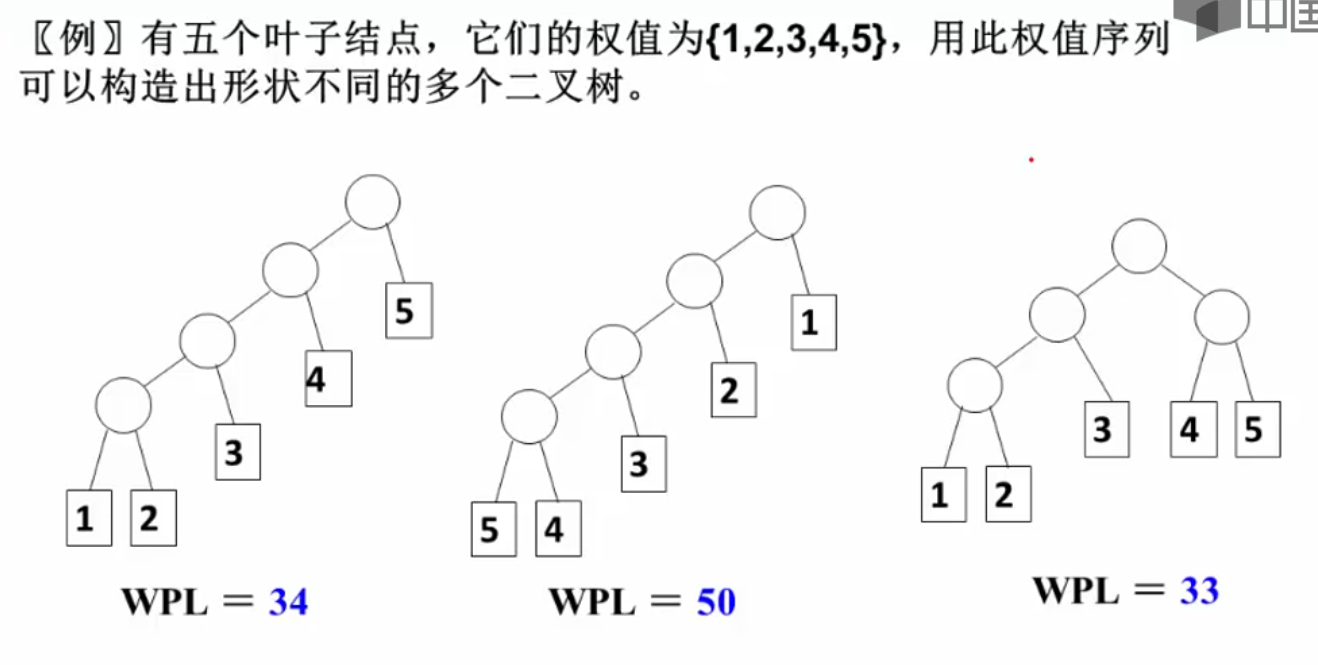
哈夫曼树的构造方法：每次把权值最小的两棵二叉树合并
例如对于节点1，2，3，4，5，构造出哈夫曼树如下：
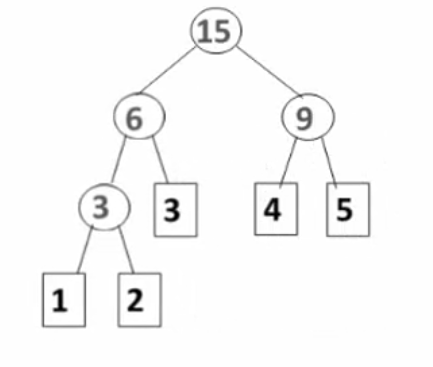
哈夫曼树的构造过程：
//定义一个最大堆：指向HeapStruct的指针
typedef struct HeapStruct* MinHeap;
typedef struct TreeNode* HaffmanTree;
typedef int ElementType;
struct HeapStruct {
ElementType* Data;
int Size;
int Capacity;
};
struct TreeNode {
int Weight;
HaffmanTree Left, Right;
};
ElementType DeleteMin(MinHeap H);
void Insert(MinHeap H, ElementType item);
HaffmanTree Huffman(MinHeap H) {
int i;
HaffmanTree T;
BuildMinHeap(H);
for (i = 0; i < H->Size; ++i) {
T = malloc(sizeof(struct TreeNode));
T->Left = DeleteMin(H);
T->Right = DeleteMin(H);
T->Weight = T->Left->Weight + T->Right->Weight;
Insert(H, T);
}
T = DeleteMin(H);
return T;
}
哈夫曼树的特点：
- 没有degree=1的节点
- n个叶子节点的哈夫曼树共有2n-1个节点
- 哈夫曼树的任意非叶子节点的左右子树交换后仍是哈夫曼树
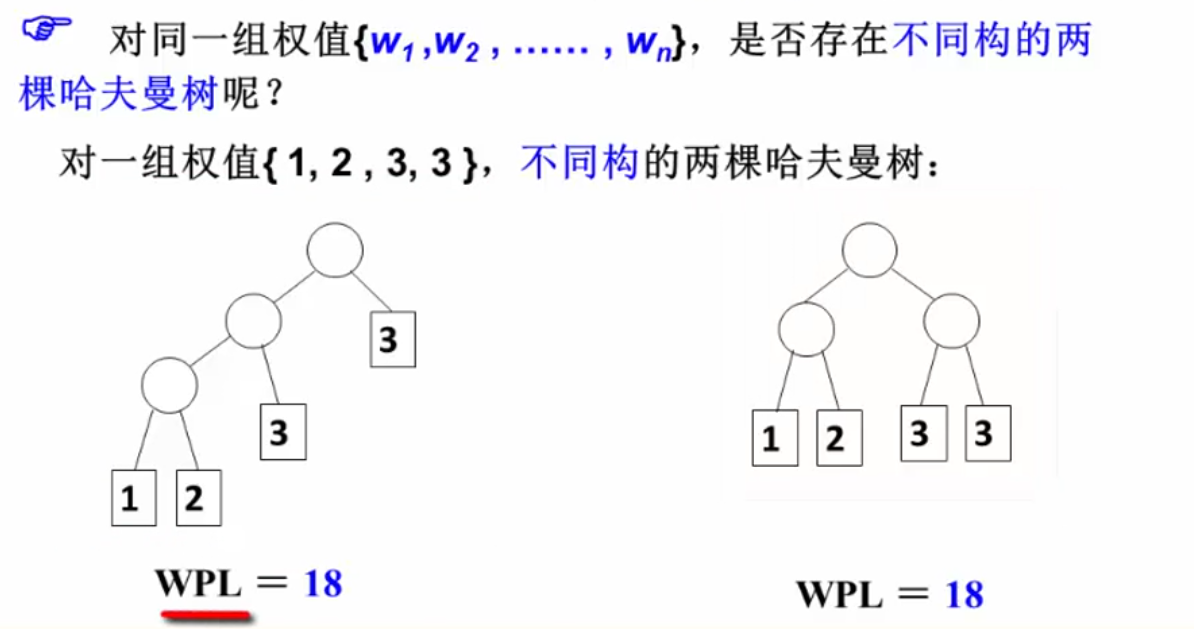
哈夫曼编码：
如何避免二义性：
采用prefix code：任何字符的编码都不是另一字符编码的前缀，如此可以实现无二义地解码
使用哈夫曼树进行编码：
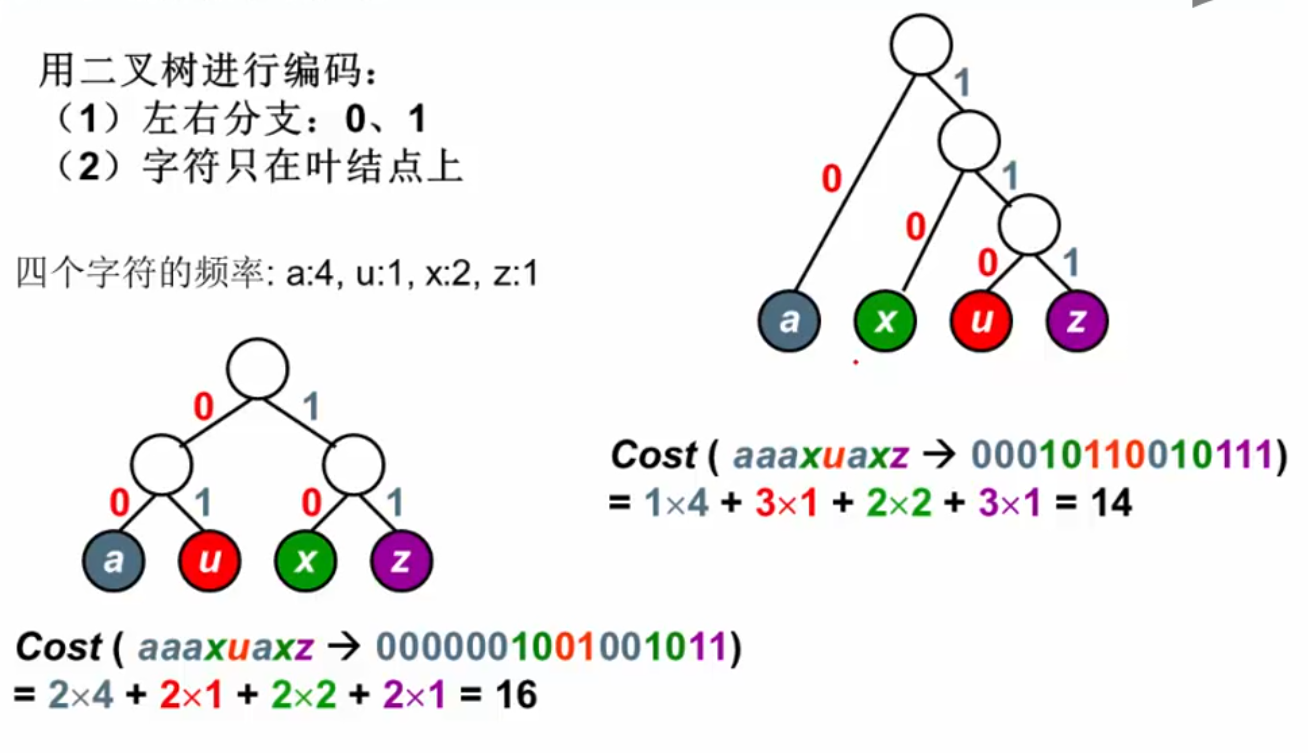
实例：
并查集
并查集问题中集合的存储用树来实现，树的每个节点代表一个集合元素：
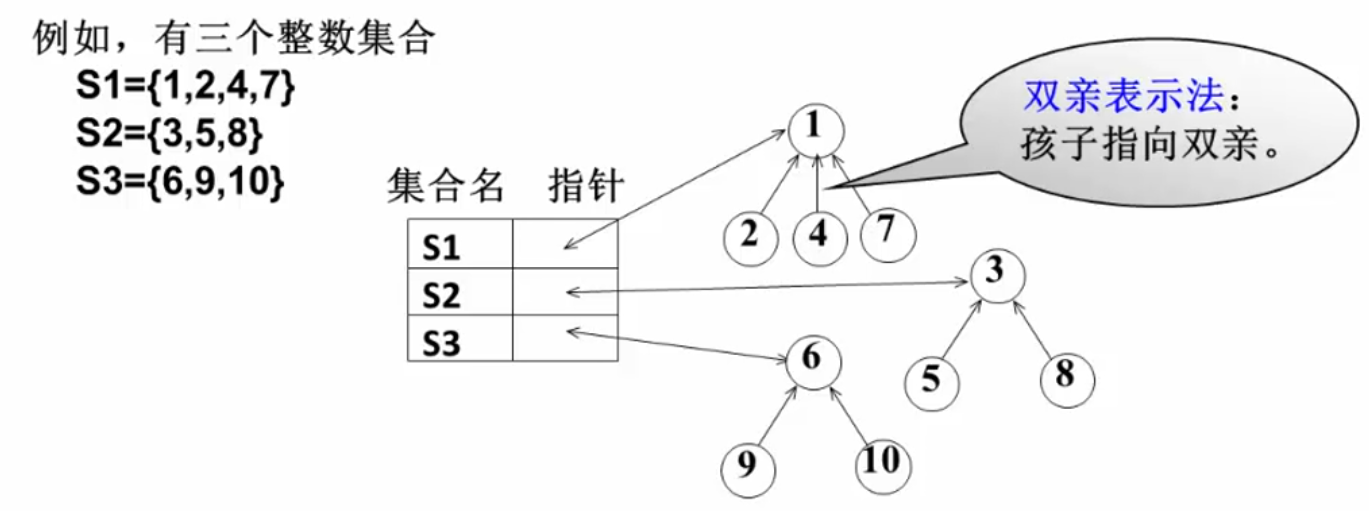
也可以采用数组存储的方式：
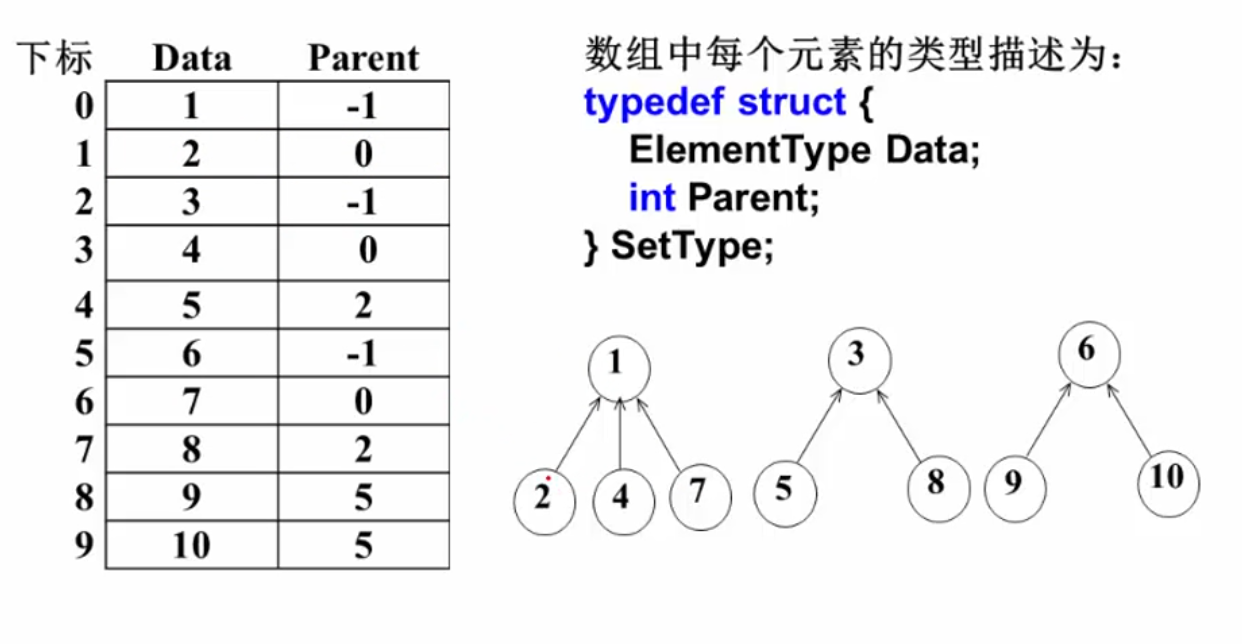
查找某个元素所在的集合（已知X求它的根节点），代码实现如下：
#define MAXSIZE 4096
//使用结构数组表示结合
typedef int ElementType;
typedef struct {
ElementType Data;
int Parent;
} SetNode;
//找到根节点下标
int Find(SetNode S[], ElementType X) {
int i = 0;
for (; i < MAXSIZE && S[i].Data != X; ++i)
;
if (i >= MAXSIZE)
return -1;
for (; S[i].Parent != -1; i = S[i].Parent)
;
return i;
}
集合的并运算：
- 分别找到X1和X2两个元素所在集合树的根节点
- 如果他们不同根，则将一个根节点的父节点指针设置成另一个根节点的数组下标
代码实现：
//集合的并运算
void Union(SetNode S[], ElementType X1, ElementType X2) {
int Root1 = Find(S, X1);
int Root2 = Find(S, X2);
if (Root1 != Root2)
S[Root2].Parent = Root1;
return;
}
考虑到越并树越高，导致查找效率变差
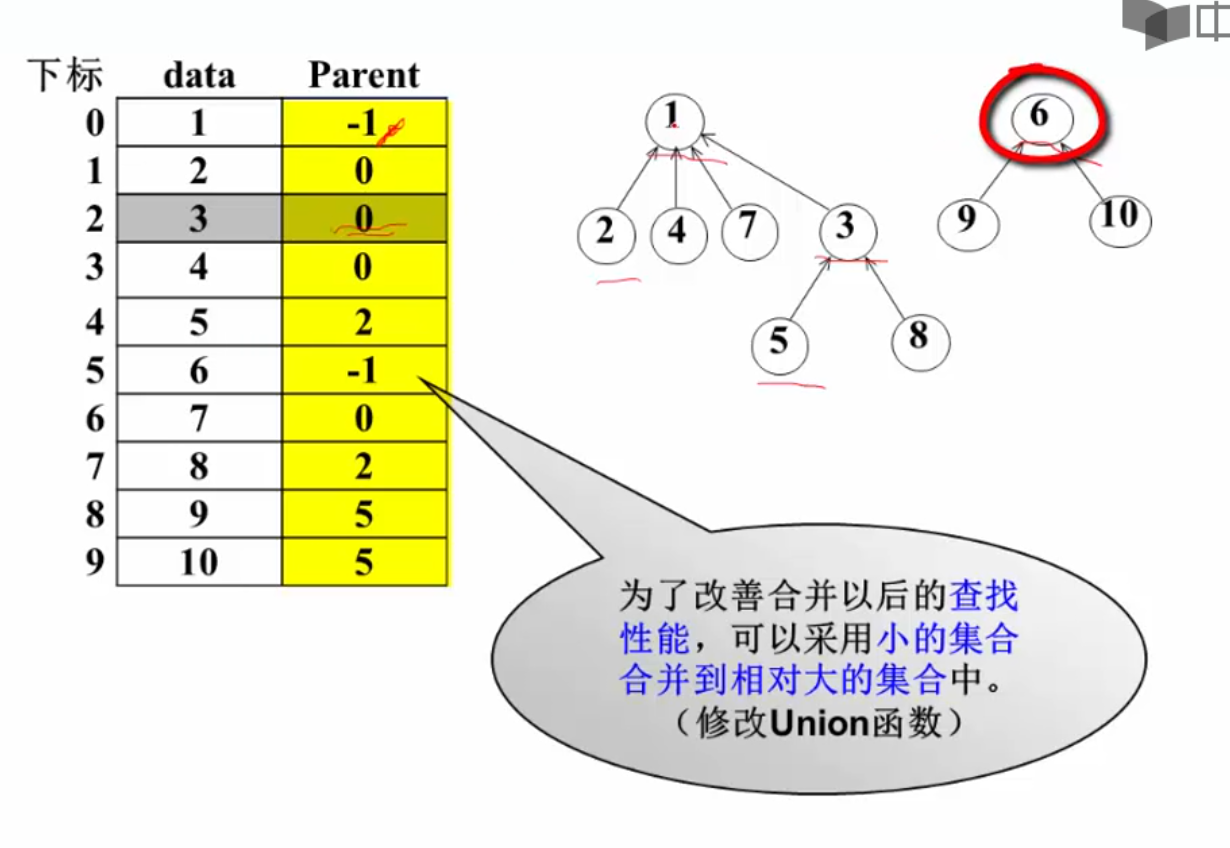
改进策略：让根节点的Parent分量存储一个有意义的负值-集合中元素的个数，这样就能知道两个集合的相对大小了
堆中的路径
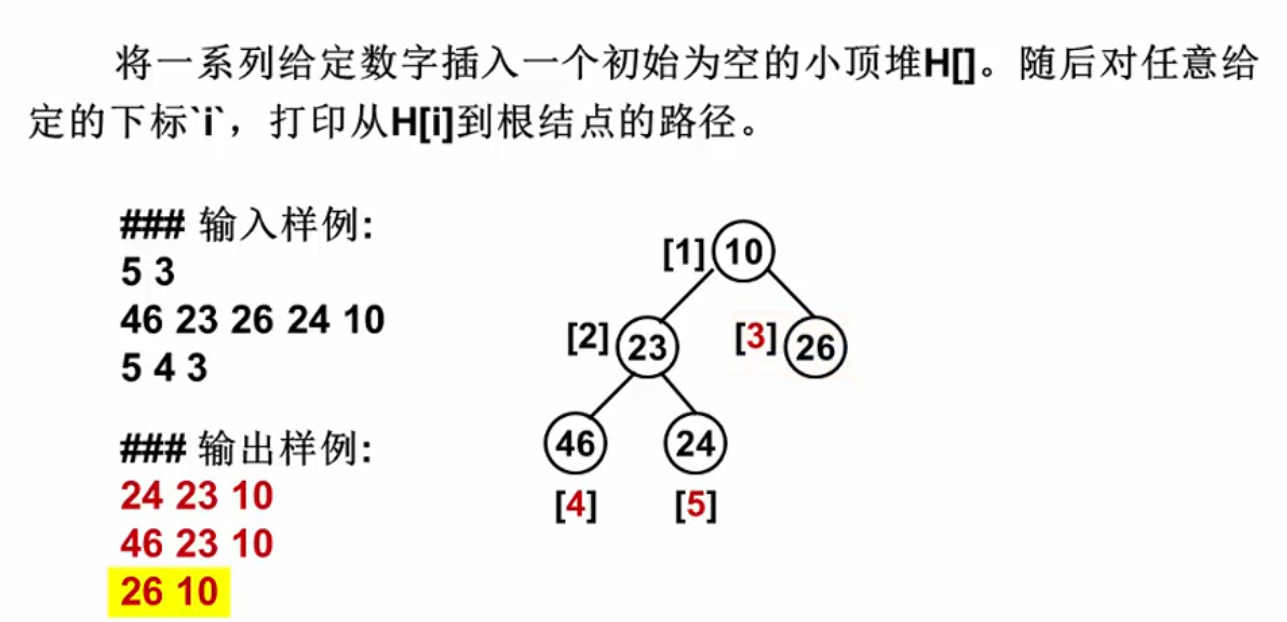
代码实现：
#include <stdio.h>
#include <stdlib.h>
#define MAXN 10000
#define MINVAL -10001
struct HeapNode {
int* data;
int size;
};
typedef struct HeapNode* Heap;
Heap createHeap(int N) {
Heap h = (Heap)malloc(sizeof(struct HeapNode));
h->data = (int*)malloc(sizeof(int) * (N + 1));
h->size = 0;
h->data[0] = MINVAL;
return h;
}
void insertHeap(Heap h, int val) {
int i;
for (i = ++h->size; h->data[i / 2] > val; i /= 2) {
h->data[i] = h->data[i / 2];
}
h->data[i] = val;
}
void destoryHeap(Heap h) {
if (h) {
if (h->data) {
free(h->data);
}
free(h);
}
}
int main() {
int N, M;
scanf("%d %d", &N, &M);
Heap h = createHeap(N);
int n;
for (int i = 0; i < N; ++i) {
scanf("%d", &n);
insertHeap(h, n);
}
for (int i = 0; i < M; ++i) {
scanf("%d", &n);
printf("%d", h->data[n]);
n /= 2;
for (; n > 0; n /= 2) {
printf(" %d", h->data[n]);
}
printf("n");
}
destoryHeap(h);
return 0;
}
FileTransfer
集合的简化表示：任何有限集合的（N个）元素都可以被一一映射为整数0~N-1
并查集代码实现：
#define MAXSIZE 1024
typedef int ElementType;
//根节点的下标作为集合名称
typedef int SetName;
typedef ElementType SetType[MAXSIZE];
SetName Find(SetType S, ElementType X) {
while (S[X] > 0)
X = S[X];
return X;
}
void Union(SetType S, SetName Root1, SetName Root2) {
//默认Root1和Root2是两个不同集合的根节点
S[Root2] = Root1;
}
输入样例1：
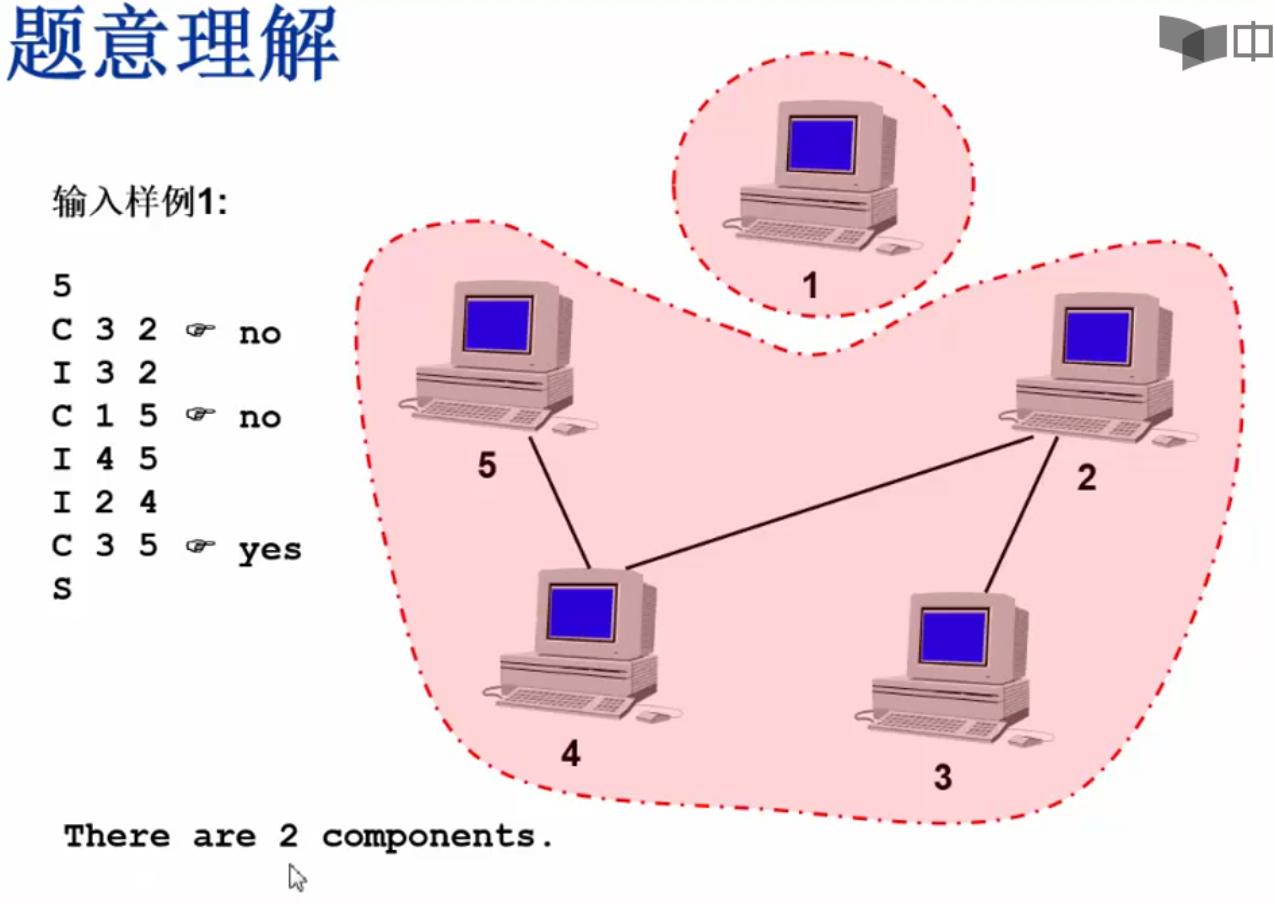
输入样例2：
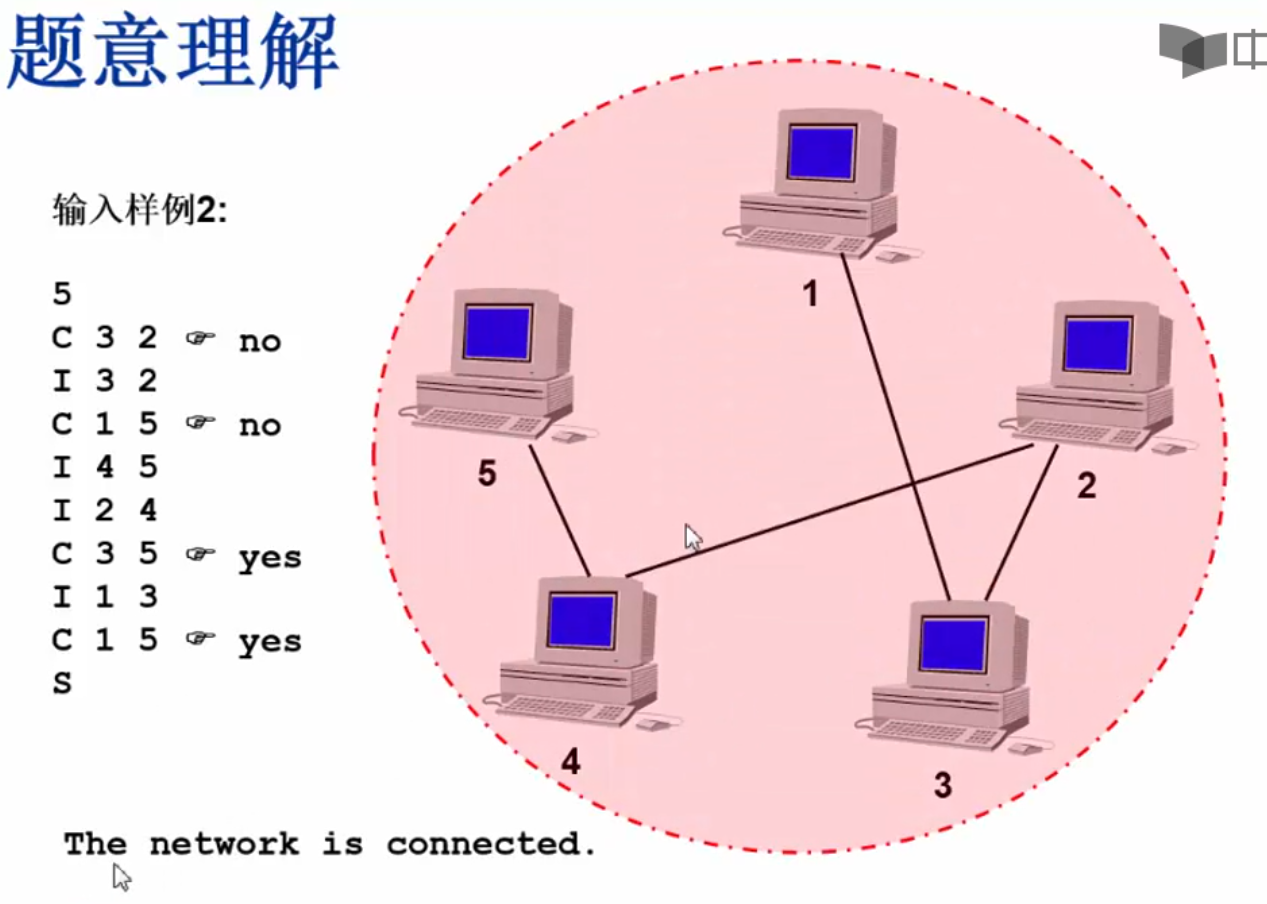
如果Find()函数和Union()函数采用上面的TSSN(too simple sometimes not work)的实现，会出现运行超时，值得优化
为了解决不断的插入导致树越来越高，我们采用按秩归并的策略：
按树高进行归并：
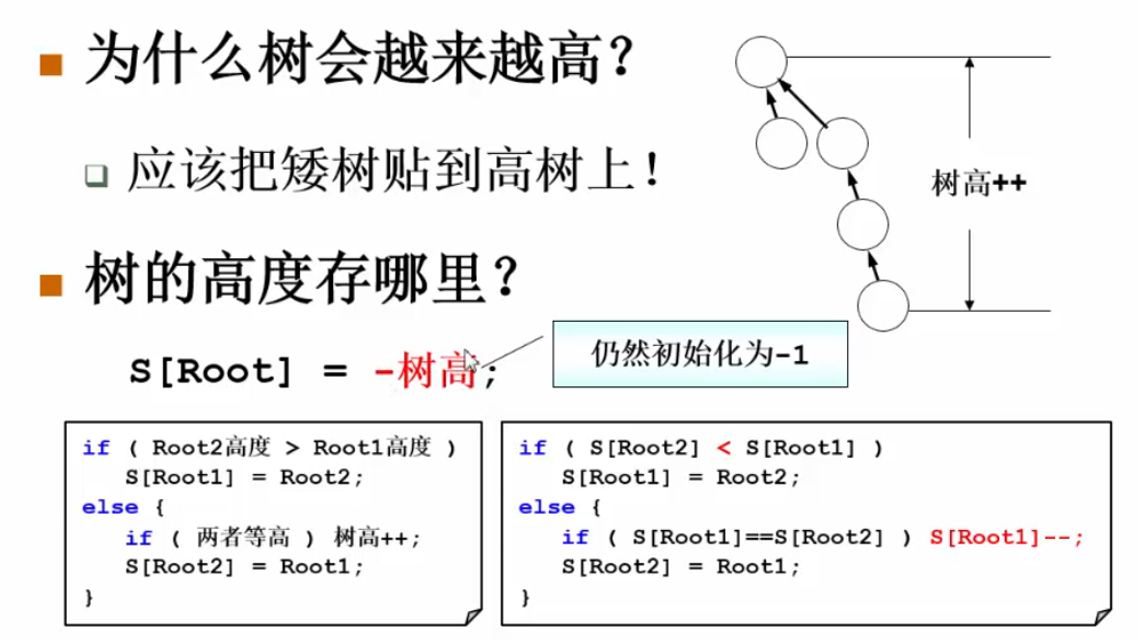
改进Union()函数：
void Union_mergeByHeight(SetType S, SetName Root1, SetName Root2) {
if (S[Root2] < S[Root1]) {
S[Root1] = Root2;
} else {
if (S[Root1] == S[Root2])
S[Root1]--;
S[Root2] = Root1;
}
}
或者按规模归并：
改进Union()函数：
void Union_mergeBySize(SetType S, SetName Root1, SetName Root2) {
if (S[Root2] < S[Root1]) {
S[Root2] += S[Root1];
S[Root1] = Root2;
} else {
S[Root1] += S[Root2];
S[Root2] = Root1;
}
}
采用路径压缩策略可以在查找时就大大降低树高：
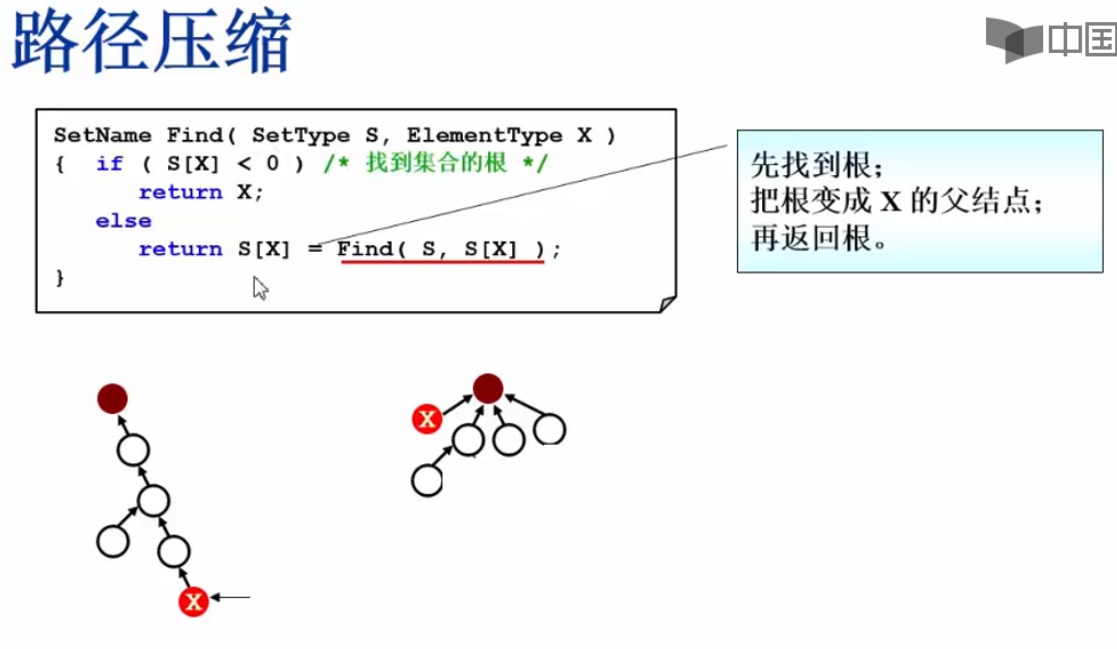
SetName Find_PathCompression(SetType S, ElementType X) {
if (S[X] < 0)
return X;
else
return S[X] = Find(S, S[X]);
}
递归返回时，会不断地将叶子节点挂接到根节点上，这大大降低了树的高度，提高了查找效率
最终的实现代码如下：
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef int SetName;
typedef int *Set;
int Find(Set S, int X) {
if (S[X] < 0) {
return X;
} else {
return S[X] = Find(S, S[X]);
}
}
void Union(Set S, SetName s1, SetName s2) {
if (S[s1] < S[s2]) {
S[s1] += S[s2];
S[s2] = s1;
} else {
S[s2] += S[s1];
S[s1] = s2;
}
}
void Input(Set S, int x, int y) {
int r1 = Find(S, x);
int r2 = Find(S, y);
Union(S, r1, r2);
}
void Check(Set S, int x, int y) {
int r1 = Find(S, x);
int r2 = Find(S, y);
if (r1 > 0 && r2 > 0 && r1 == r2) {
printf("yesn");
} else {
printf("non");
}
}
void Components(Set S, int N) {
int cnt = 0;
for (int i = 1; i <= N; ++i) {
if (S[i] < 0) {
cnt++;
}
}
if (cnt > 1) {
printf("There are %d components.n", cnt);
} else {
printf("The network is connected.n");
}
}
int main() {
int N, x, y;
scanf("%dn", &N);
Set S = (Set) malloc(sizeof(int) * (N + 1));
for (int i = 0; i < N + 1; ++i) {
S[i] = -1;
}
char cmd;
scanf("%c", &cmd);
while (1) {
scanf(" %d %dn", &x, &y);
switch (cmd) {
case 'C':
Check(S, x, y);
break;
case 'I':
Input(S, x, y);
break;
}
scanf("%c", &cmd);
if (cmd == 'S') {
Components(S, N);
return 0;
}
}
return 0;
}
Tree Traversals Again
题意理解：
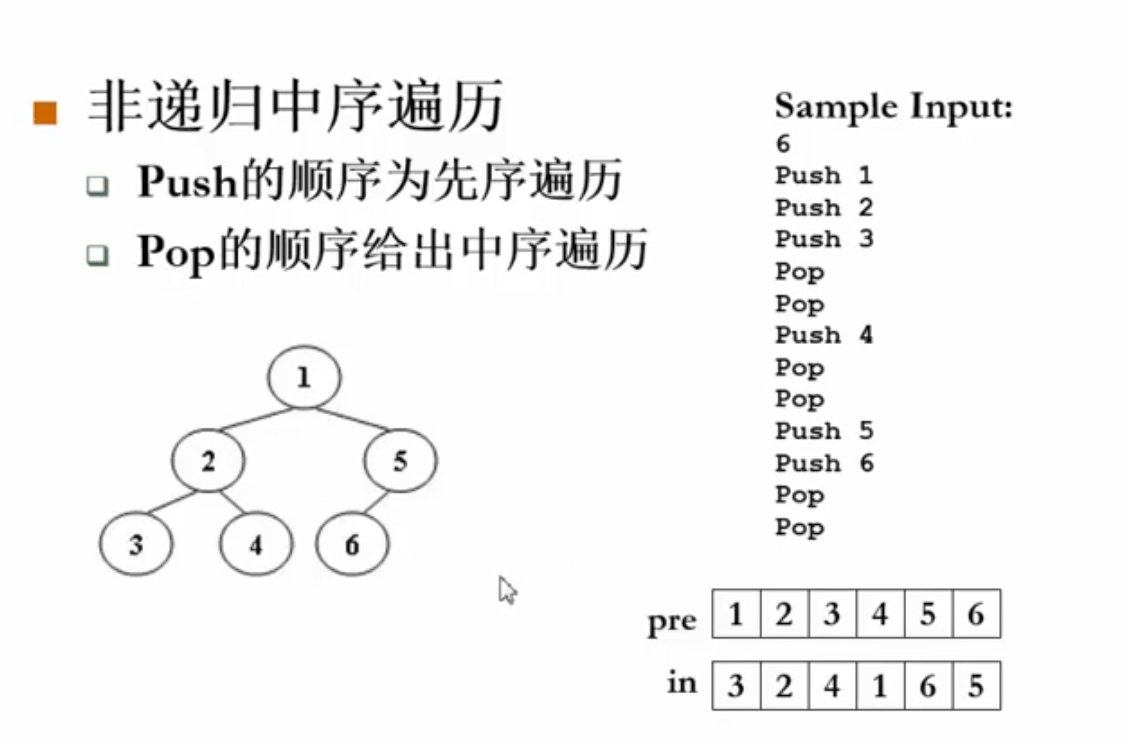
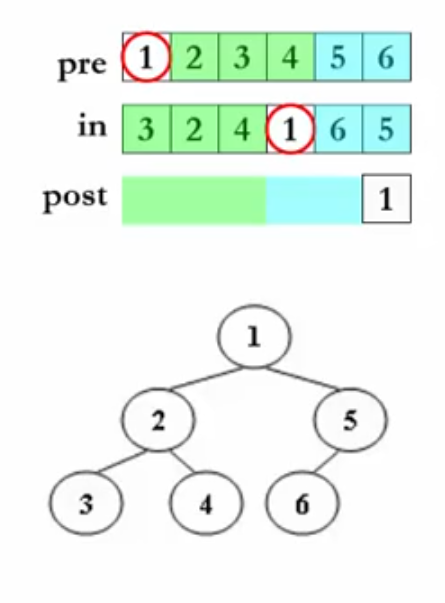
首先根据先序遍历结果pre确定根节点为1，放在后序遍历数组post的最后面。然后根据中序遍历数组in中1的位置将pre一分为二，分别是左右子树，然后递归地解决
代码实现：
#include <vector>
#include <list>
#include <stack>
#include <string>
#include <iostream>
using namespace std;
void solve(const vector<int> &pre, const vector<int> &in, list<int> &post) {
if (pre.size() == 0) {
return;
}
int r = pre[0];
post.push_front(r);
if (pre.size() == 1) {
return;
}
int i = 0;
for (; i < in.size() && in[i] != r; ++i);
vector<int> preL = vector<int>(pre.begin() + 1, pre.begin() + 1 + i);
vector<int> inL = vector<int>(in.begin(), in.begin() + i);
vector<int> preR = vector<int>(pre.begin() + 1 + i, pre.end());
vector<int> inR = vector<int>(in.begin() + 1 + i, in.end());
solve(preR, inR, post);
solve(preL, inL, post);
}
int main() {
int N, n;
cin >> N;
string cmd;
vector<int> preorder;
vector<int> inorder;
list<int> postorder;
stack<int> stk;
for (int i = 0; i < 2 * N; ++i) {
cin >> cmd;
if (cmd == "Push") {
cin >> n;
preorder.push_back(n);
stk.push(n);
} else {
inorder.push_back(stk.top()), stk.pop();
}
}
solve(preorder, inorder, postorder);
bool flag = true;
for (list<int>::iterator it = postorder.begin(); it != postorder.end(); ++it) {
if (flag) {
flag = false;
} else {
cout << " ";
}
cout << *it;
}
return 0;
}
Complete Binary Search Tree
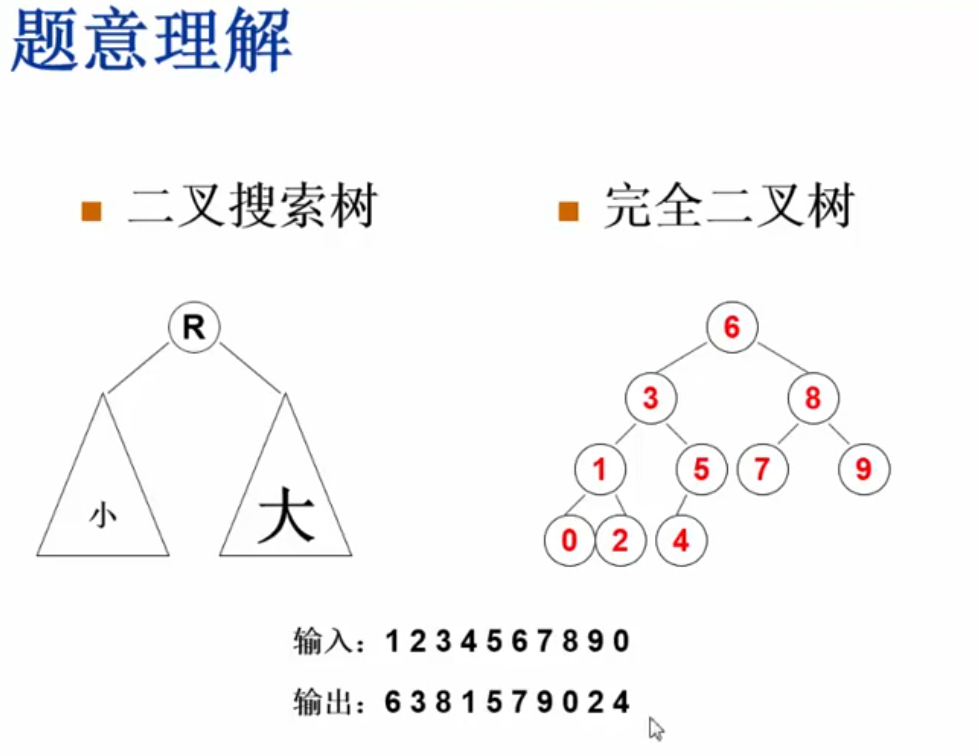
输入一个序列，输出由它构建的完全二叉搜索树的层序遍历结果
采用什么物理结构存储：
完全二叉树采用数组表示不会浪费空间，而且数组中的元素顺序就是层序遍历的顺序
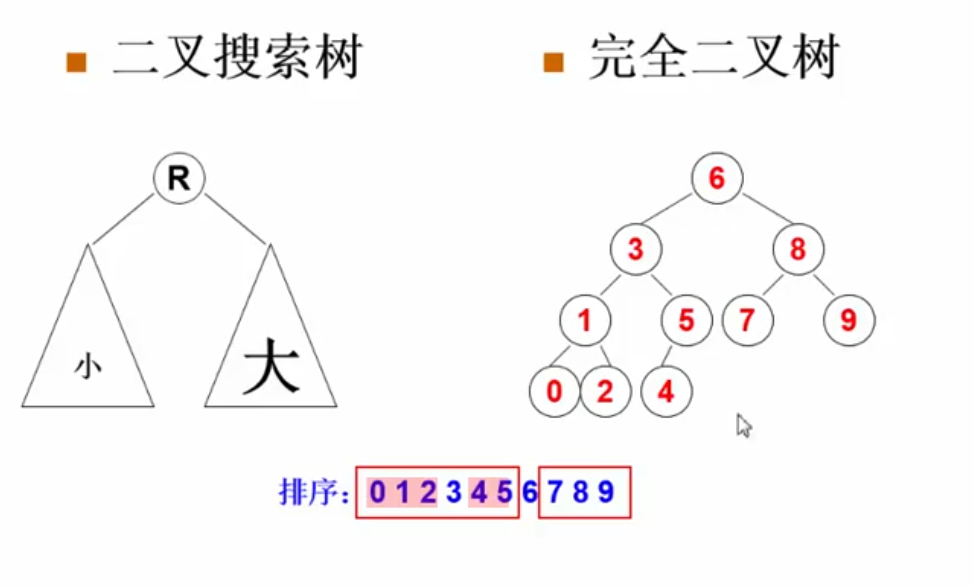
完全二叉树结构完全由n决定，当n==10，左子树有6个节点，右子树有3个节点，故根节点为6，左边6个归左子树，右边3个归右子树，然后递归地进行
代码实现：
void solve(int ALeft, int ARight, int TRoot) {
int n = ARight - ALeft + 1;
if (n == 0)
return;
int L = getLeftLength(n);
T[TRoot] = A[ALeft + L];
int LeftRoot = TRoot * 2 + 1;
int RightRoot = LeftRoot + 1;
solve(ALeft, ALeft + L - 1, LeftRoot);
solve(ALeft + L + 1, ARight, RightRoot);
return;
}
关于qsort()：
该函数可进行复杂排序，compare传入的是一个比较函数，像strcmp()这种的，类似于C++中谓词的概念
计算左子树的规模：
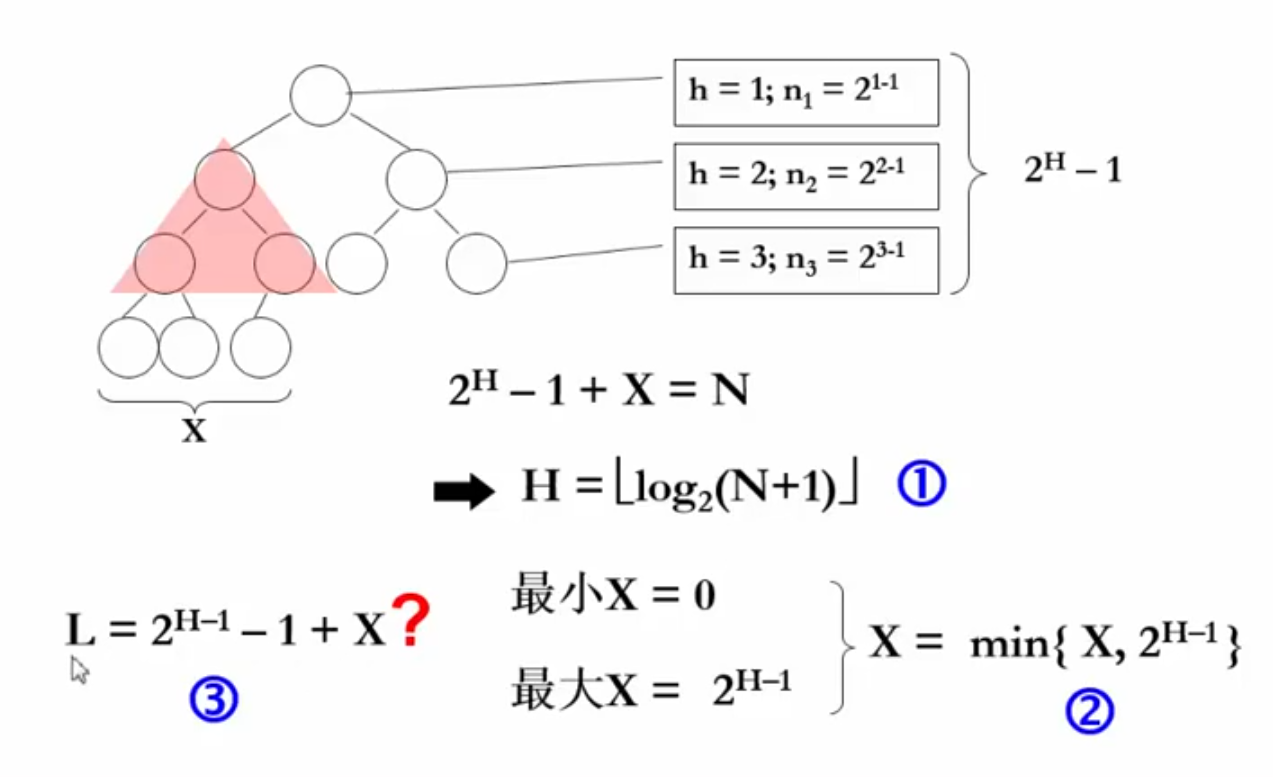
对于第H层下的第H+1层多出来了X个节点，求左子树规模时，X最大取2^(H-1)，也就是该第H+1层节点数的一半，多出来的都到右子树了。故X=min{X,2^(H-1)}。
然后再加上其上面的完全二叉树的节点个数((2^H-1)-1)/2=2^(H-1)-1，就是左子树的规模
完整代码实现：
#include <math.h>
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
int getLeftLength(int n) {
int h = (int) (log(n) / log(2));
int x = n + 1 - pow(2, h);
x = min(x, (int) pow(2, h - 1));
return x + pow(2, h - 1) - 1;
}
void solve(int ALeft, int ARight, int TRoot, vector<int> &A, vector<int> &T) {
int N = ARight - ALeft + 1;
if (N == 0) {
return;
}
int ll = getLeftLength(N);
int ARoot = ALeft + ll;
T[TRoot] = A[ARoot];
int TLefeRoot = TRoot * 2 + 1;
int TRightRoot = TLefeRoot + 1;
solve(ALeft, ARoot - 1, TLefeRoot, A, T);
solve(ARoot + 1, ARight, TRightRoot, A, T);
}
int main() {
int N, n;
vector<int> A;
vector<int> T;
cin >> N;
for (int i = 0; i < N; ++i) {
cin >> n;
A.push_back(n);
}
sort(A.begin(), A.end());
T.resize(N);
solve(0, N - 1, 0, A, T);
bool flag = true;
for (int i = 0; i < N; ++i) {
if (flag) {
flag = false;
} else {
cout << " ";
}
cout << T[i];
}
}
本质还是根据一个有序序列重建BST，力扣上还有类似的题目：
108. 将有序数组转换为二叉搜索树
109. 有序链表转换二叉搜索树
Huffman Codes
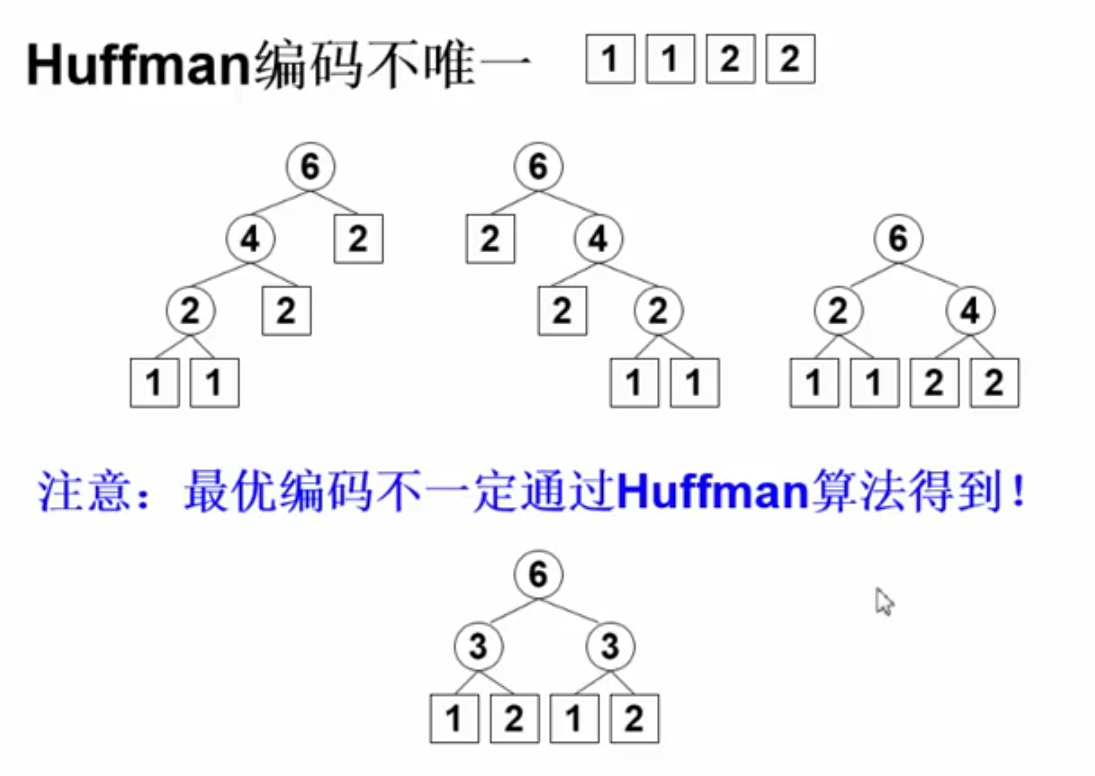
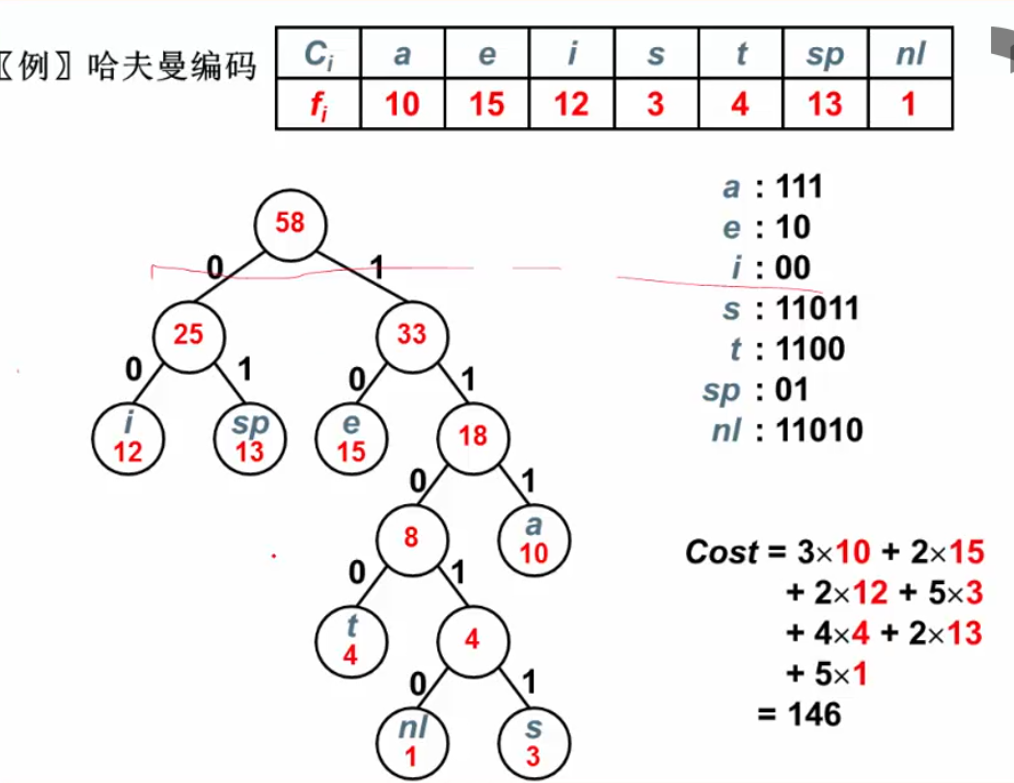
哈夫曼编码的特点：
- 最优编码-总长度(WPL)最小
- 无歧义解码-前缀码：数据仅存在于叶子节点
- 没有degree=1的节点：满足1和2必定满足3
计算最优编码的长度：
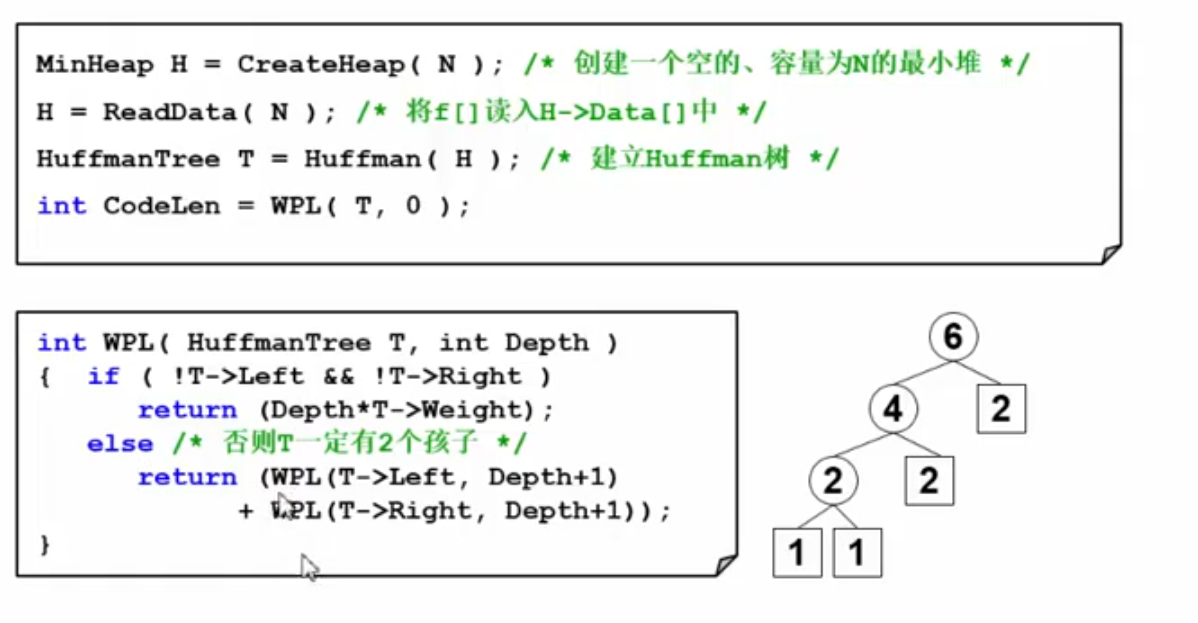
核心算法：
约定左0右1
四、图
图的定义和表示
图用来表示多对多的关系，一般包含以下内容：
- 一组顶点：通常用V(Vertex)表示顶点的集合
- 一组边：通常用E(Edge)表示边的集合
图的ADT描述：
图的邻接矩阵表示法：G[N][N]表示N个顶点从0到N-1编号
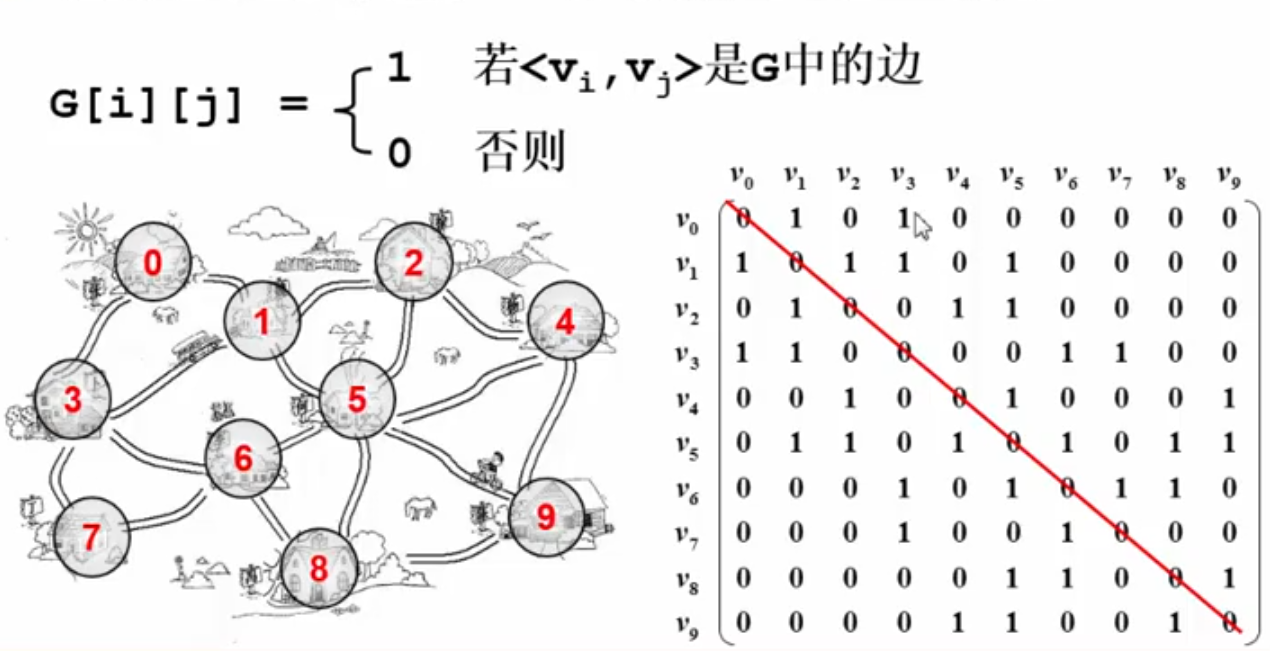
特点：对角线上元素都是0；如果表示的图为无向图，则矩阵为对称矩阵
为了节省空间，也采用一维数组存储：
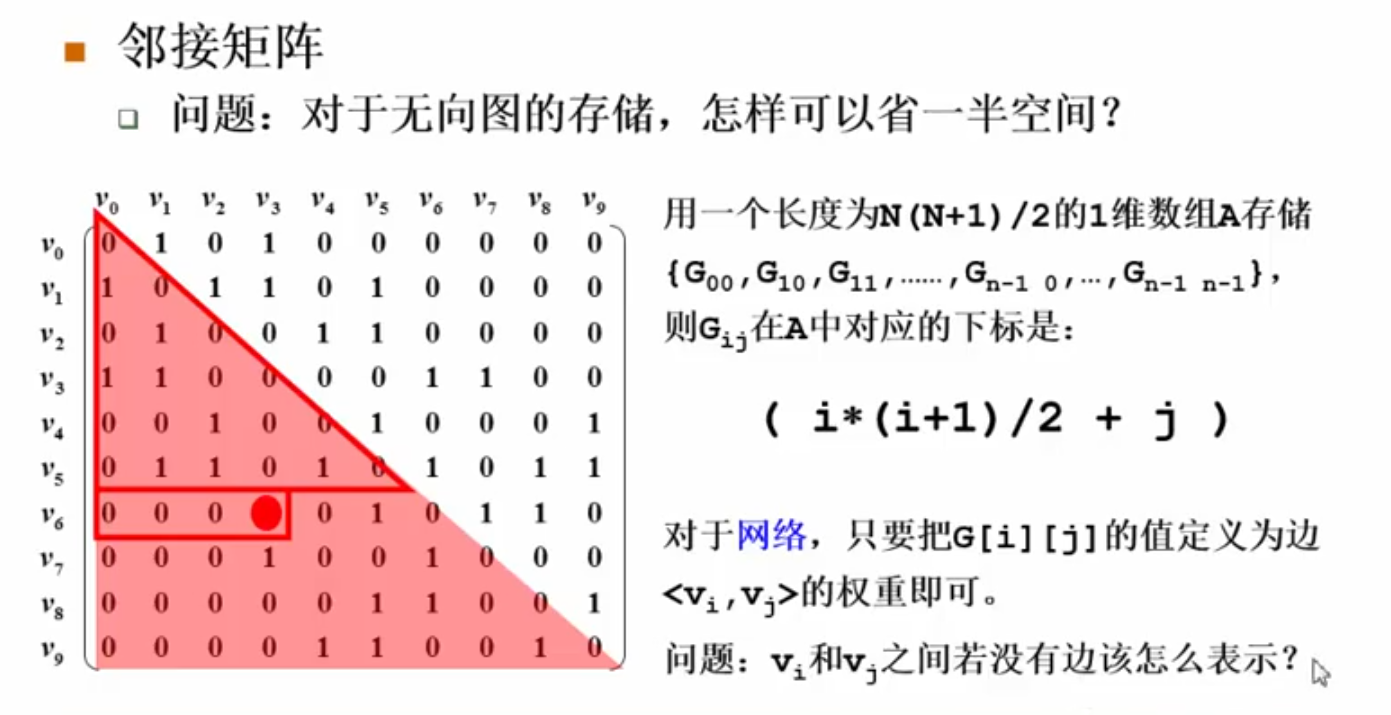
Gij在A中对应的下标是i*(i+1)/2+j
邻接矩阵的优缺点：
完全图：任意两个顶点之间都有一条边，也就是说边数达到了极大
图的邻接表表示法：G[N]为指针数组，对应矩阵每行一个链表，只存非0元素
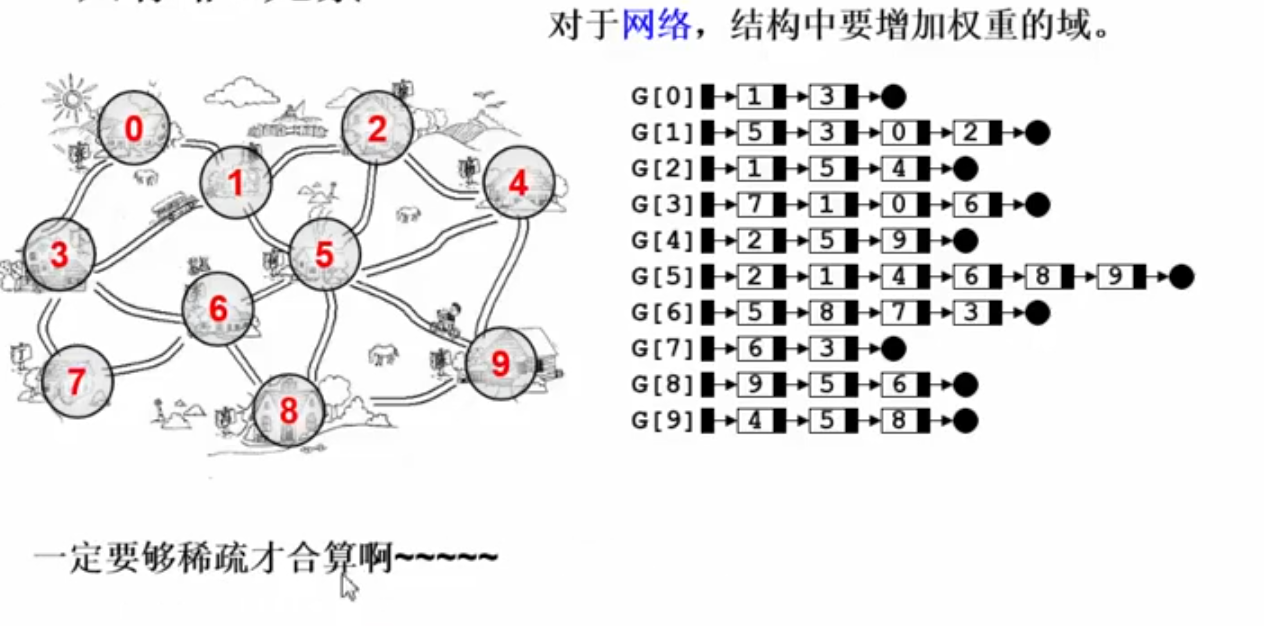
邻接表优缺点：
正邻接表：将邻接矩阵的每一行存成一个链表
逆邻接表：将邻接矩阵的每一列存成一个链表，存指向自己的边
图的表示不只有邻接矩阵和邻接表这两种表示方法
图的遍历
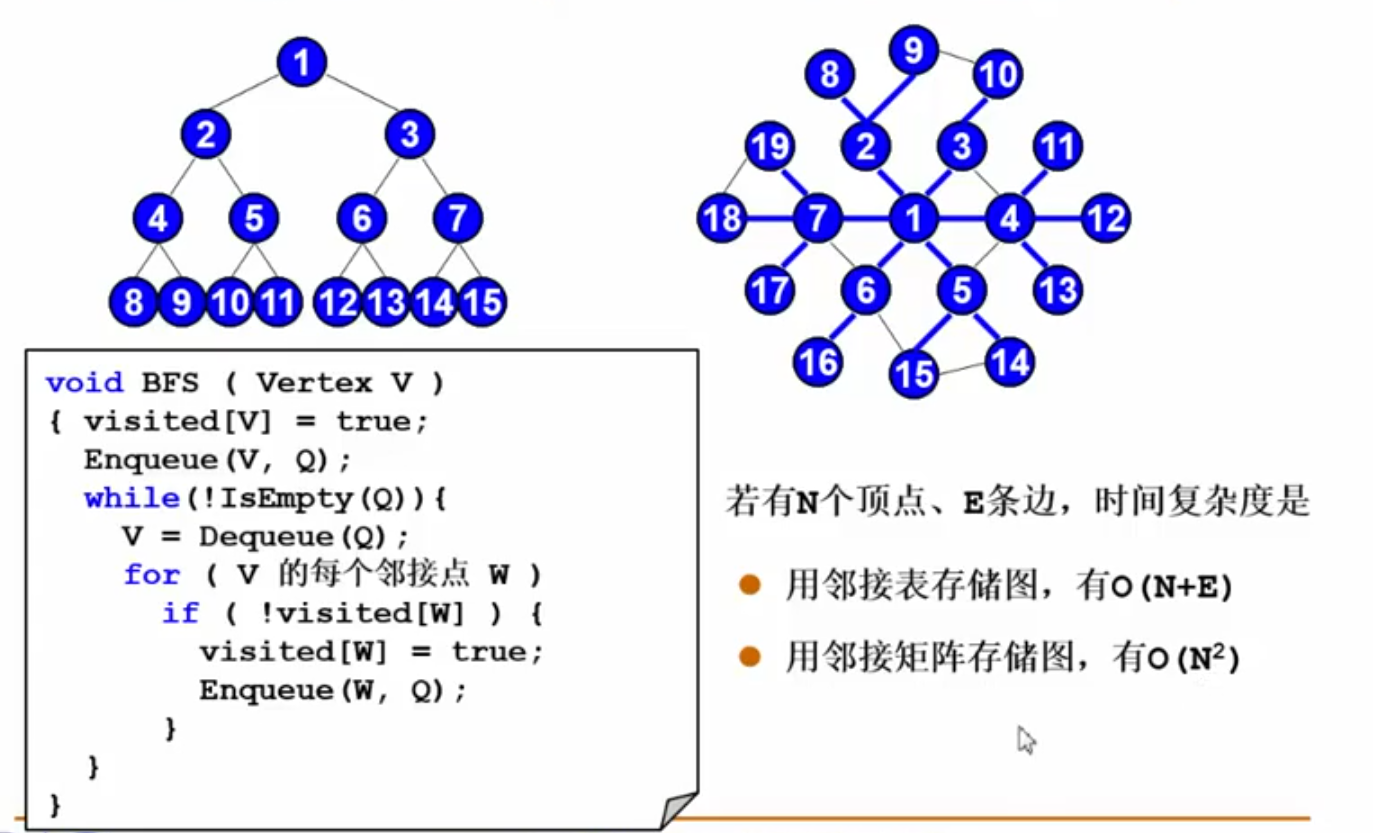
Depth First Search：
若有V个顶点，E条边，时间复杂度是：
- 用邻接表表示图：
O(V+E) - 用邻接矩阵表示图：
O(V^2)
Breadth First Search：
为什么需要两种遍历呢？
比如对于迷宫问题：我们规定邻接点访问顺序是从其最上方节点开始顺时针的8邻域节点，绿色为出口，DFS的结果如下：
相较而言，BFS是一圈一圈往外搜索的，要省力气的多
当然BFS省力是因为出口位置的选择离入口不远，如果出口在最右边，DFS会更省力
图不连通怎么办？
连通：如果从V到W之间存在一条（无向）路径，则称V和W是连通的
路径：V到W的路径是一系列顶点{V,v1,v2,...,W}的集合，其中任一对相邻的顶点间都有图中的边
路径的长度：路径中的边数，如果带权，则是所有边的权重和
简单路径：V到W之间的所有顶点都不同
回路：起点等于终点的路径
连通图：图中任意两顶点均连通
对于无向图：
连通分量：无向图的极大连通子图
- 极大顶点数：再加1个顶点就不连通了。
- 极大边数：包含子图中所有顶点相连的所有边
对于有向图：
强连通：有向图中顶点V和W之间存在双向路径，则称V和W是强连通的
强连通图：有向图中任意两顶点均强连通
强连通分量：有向图的极大强连通子图
所以当图不连通时，我们需要对每一个节点都做DFS或BFS：
void DFS(Vertex V){
visited[V]=true;
for(V的每个邻接点W){
if(!visited[W])
DFS(W);
}
}
void ListComponents(Graph G){
for(each V in G){
if(!visited[V]){
DFS(V);/*or BFS(V)*/
}
}
}
Saving James Bond - Easy Version
伪码描述：
void Save007(Graph G){
for(each V in G){
if(!visited[V]&&FirstJump(V)){
answer=DFS(V);
if(answer=="YES")
break;
}
}
if(answer==YES)
output("yes");
else
output("no");
}
DFS的伪码描述：
int DFS(Vertex V){
visited[V]=true;
if(IsSafe(V)){
answer=YES;
}else{
for(each W in G){
if(!visited[W]&&Jump(V,W)){
answer=DFS(W);
if(answer==YES)
break;
}
}
}
return answer;
}
六度空间
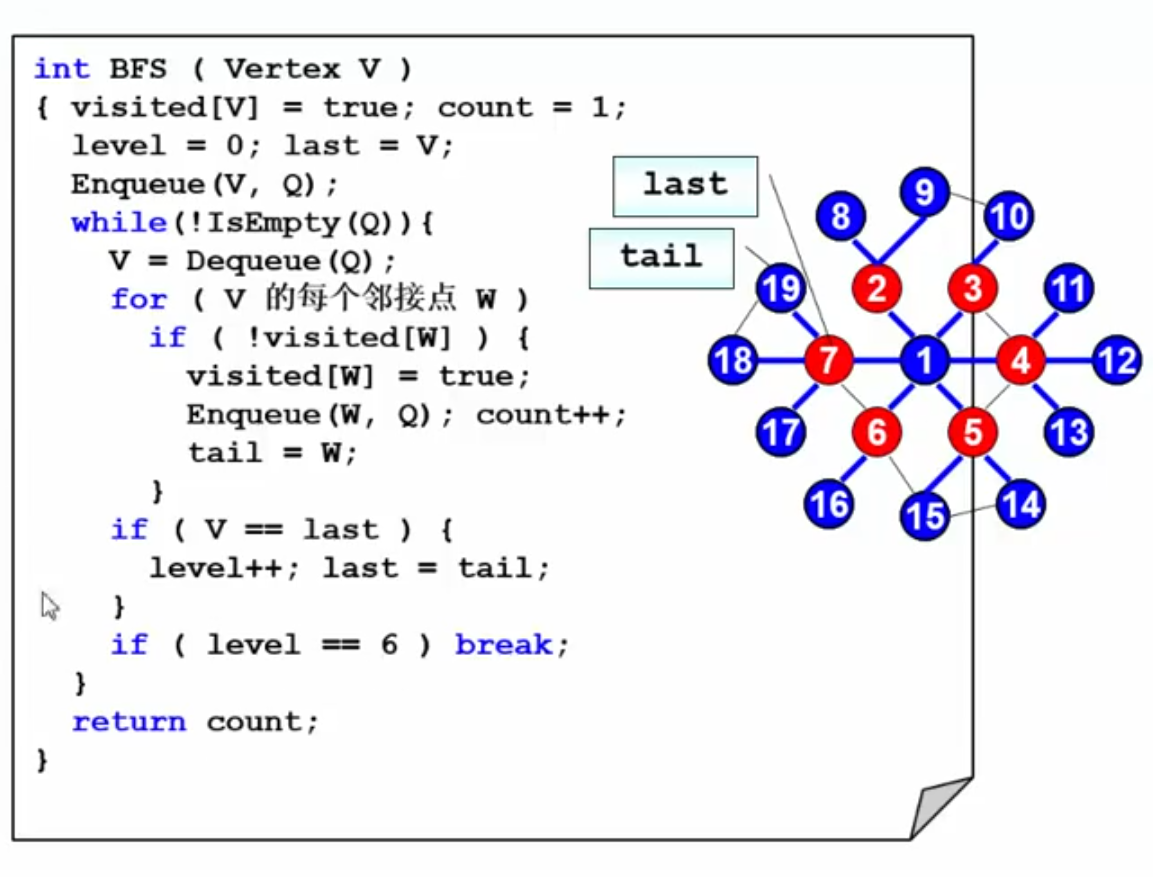
如何建立图
用邻接矩阵表示图：
代码实现：
#define MAXVERTEXNUM 100
typedef int WeightType;
typedef struct GNode* PtrToGNode;
typedef PtrToGNode MGraph;
typedef char DataType;
struct GNode {
int Nv;
int Ne;
WeightType G[MAXVERTEXNUM][MAXVERTEXNUM];
DataType Data[MAXVERTEXNUM];
};
图的初始化代码实现：
//初始化一个有Vertex个顶点但没有边的图
MGraph CreateGraph(int VertexNum) {
Vertex V, W;
MGraph Graph;
Graph = (MGraph)malloc(sizeof(struct GNode));
Graph->Ne = 0;
Graph->Nv = VertexNum;
for (V = 0; V < VertexNum; ++V) {
for (W = 0; W < VertexNum; ++W)
Graph->G[V][W] = 0;
}
return Graph;
}
向MGraph中插入边，代码实现：
void InsertEdge(MGraph Graph, Edge E) {
Graph->G[E->V1][E->V2] = E->Weight;
//如果是无向图，另一个方向也要插入
Graph->G[E->V2][E->V1] = E->Weight;
return;
}
信息由以下的输入格式给出：
代码实现：
MGraph BuildGraph() {
int Nv, i;
scanf("%d", &Nv);
MGraph Graph = CreateGraph(Nv);
scanf("%d", &(Graph->Ne));
if (Graph->Ne != 0) {
Edge E = (Edge)malloc(sizeof(struct ENode));
for (i = 0; i < Graph->Ne; ++i) {
scanf("%d %d %d", &(E->V1), &(E->V2), &(E->Weight));
InsertEdge(Graph, E);
}
free(E);
}
//如果节点中存有数据
for (Vertex V = 0; V < Graph->Nv; ++V) {
scanf("%c", &(Graph->Data[V]));
}
return Graph;
}
极简方式实现：
用邻接表表示图：
代码实现：
#define MAXVERTEXNUM 100
#define INFINITY INT_MAX
typedef int WeightType;
typedef int Vertex;
typedef char DataType;
typedef struct ENode* PtrToENode;
typedef PtrToENode Edge;
typedef struct AdjVNode* PtrToAdjVNode;
typedef struct GNode* PtrToGNode;
typedef PtrToGNode LGraph;
struct ENode {
Vertex V1, V2;
WeightType Weight;
};
struct AdjVNode {
Vertex AdjV;
WeightType Weight;
PtrToAdjVNode Next;
};
typedef struct VNode {
PtrToAdjVNode FirstEdge;
//存放顶点数据，可无
DataType Data;
} AdjList[MAXVERTEXNUM];
struct GNode {
int Nv;
int Ne;
AdjList G;
};
建立一个图：
LGraph CreateGraph(int VertexNum) {
LGraph Graph = (LGraph)malloc(sizeof(struct GNode));
Graph->Nv = VertexNum;
Graph->Ne = 0;
for (Vertex v = 0; v < VertexNum; ++v) {
Graph->G[v].FirstEdge = NULL;
}
return Graph;
}
插入边：
void InsertEdge(LGraph Graph, Edge E) {
PtrToAdjVNode NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
NewNode->AdjV = E->V2;
NewNode->Weight = E->Weight;
NewNode->Next = Graph->G[E->V1].FirstEdge;
Graph->G[E->V1].FirstEdge = NewNode;
//如果是无向图，反向也要插入
NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
NewNode->AdjV = E->V1;
NewNode->Weight = E->Weight;
NewNode->Next = Graph->G[E->V2].FirstEdge;
Graph->G[E->V2].FirstEdge = NewNode;
return;
}
完整地建立一张图：
LGraph BuildGraph() {
int Nv, i;
scanf("%d", &Nv);
LGraph Graph = CreateGraph(Nv);
scanf("%d", &(Graph->Ne));
if (Graph->Ne != 0) {
Edge E = (Edge)malloc(sizeof(struct ENode));
for (i = 0; i < Graph->Ne; ++i) {
scanf("%d %d %d", &(E->V1), &(E->V2), &(E->Weight));
InsertEdge(Graph, E);
}
free(E);
}
//如果节点中存有数据
for (Vertex V = 0; V < Graph->Nv; ++V) {
scanf("%c", &(Graph->G[V].Data));
}
return Graph;
}
最短路问题-BFS算法
问题分类：
无权图的单源最短路，可以采用BFS的思想，一圈一圈向外寻找最短路：
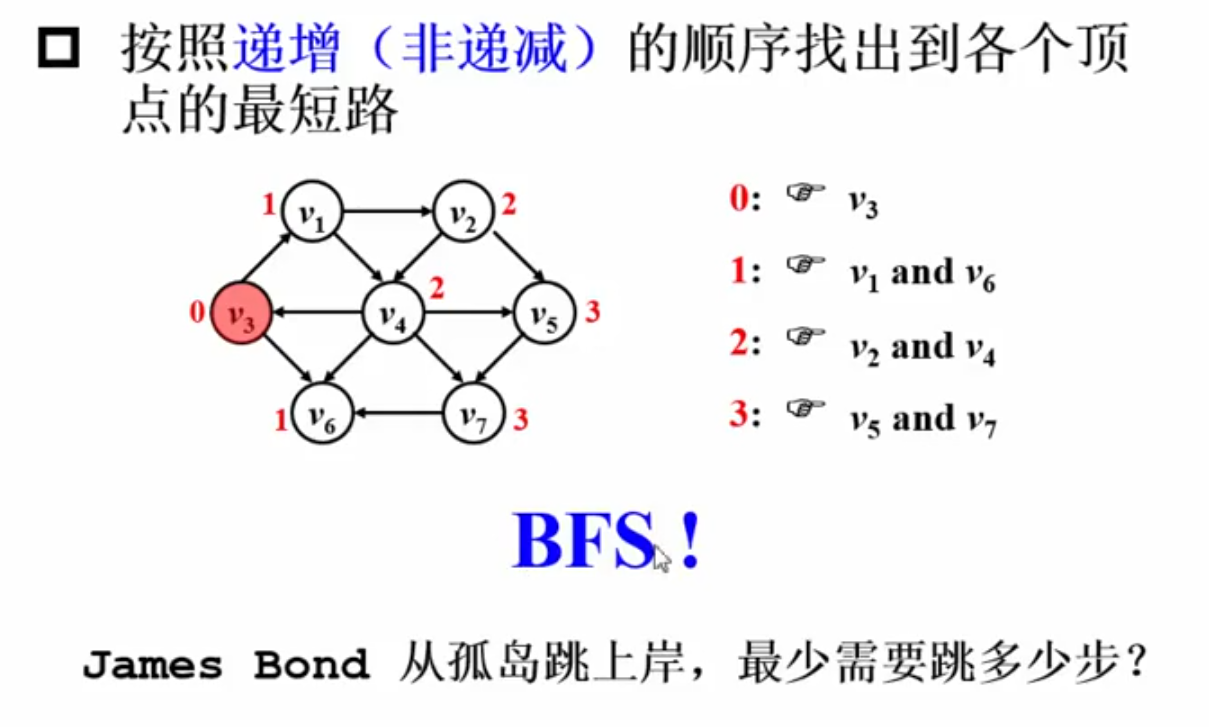
每个顶点访问了两次，每条边访问了一次，复杂度为O(2V+E)
伪码描述：
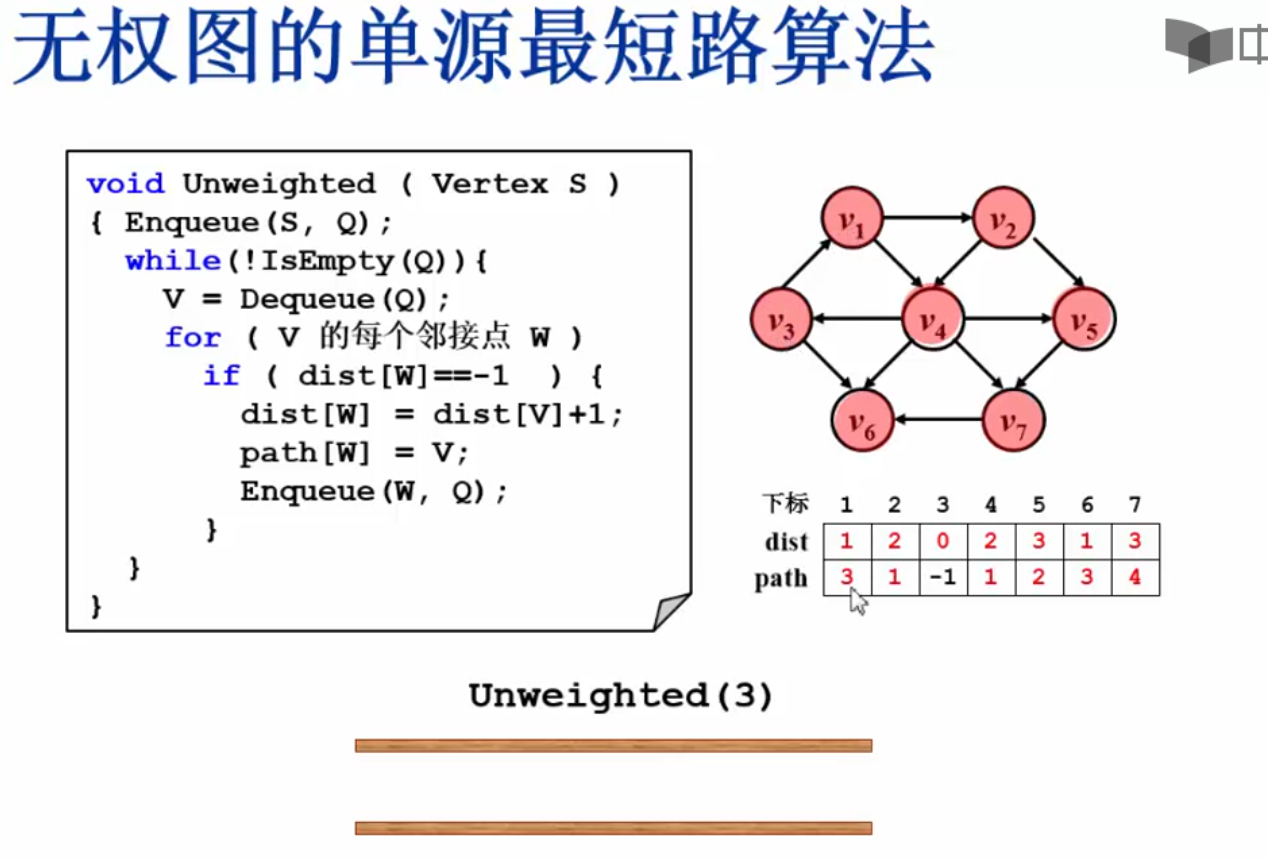
void Unweighted (Vertex S) {
EnQueue(S,Q);
while(!IsEmpty(Q)) {
V=DeQueue(Q);
for(V的每个邻接点W) {
if(dist[W]==-1) {
dist[W]=dist[V]+1;
path[W]=V;
EnQueue(W,Q);
}
}
}
}
无权图的单源最短路示例：
最短路问题-Dijskstra算法
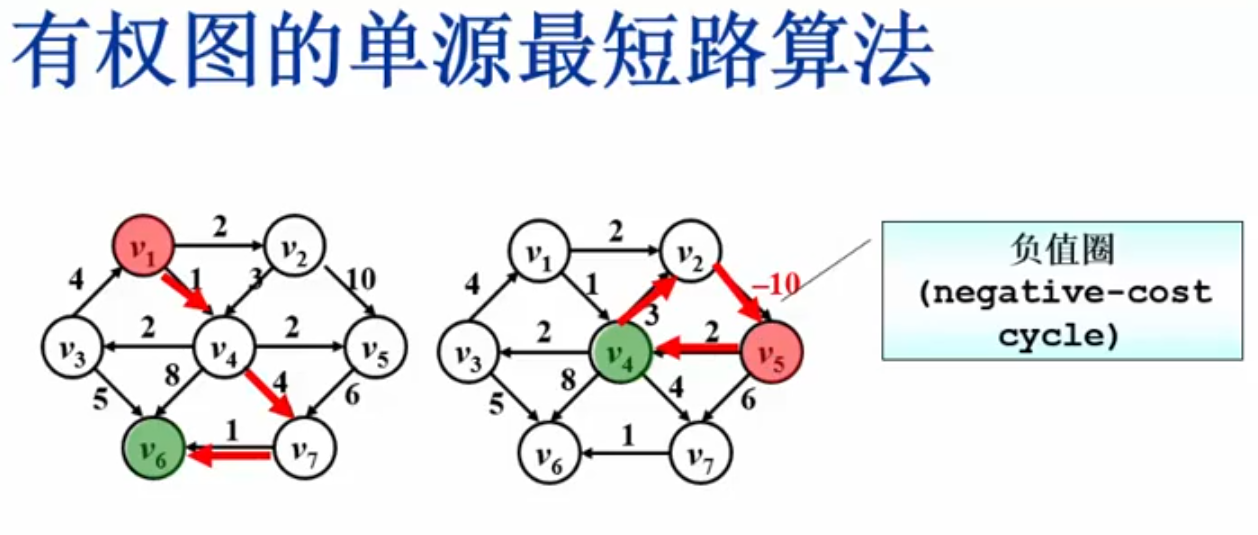
按照递增的顺序找到到各个顶点的最短路
伪码描述：
void Dijsktra(Vertex V){
while(1){
V=未收录顶点中dist最小者;
if(V不存在)
break;
collected[V]=true;
for(V的每个邻接点W){
if(!collected[W]){
if(dist[V]+E(V,W)<dist[W]){
dist[W]=dist[V]+E(V,W);
path[W]=V;
}
}
}
}
}
第一步如何做会影响时间复杂度：
有权图的单源最短路示例：
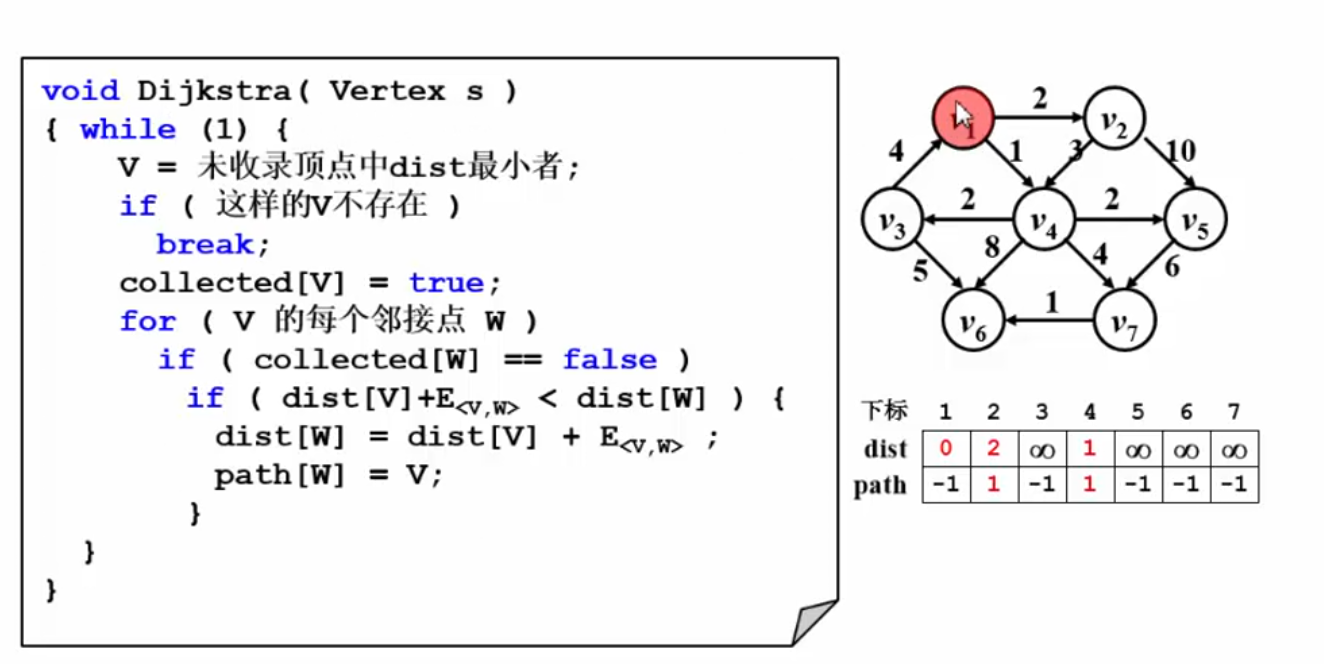
最终的结果：
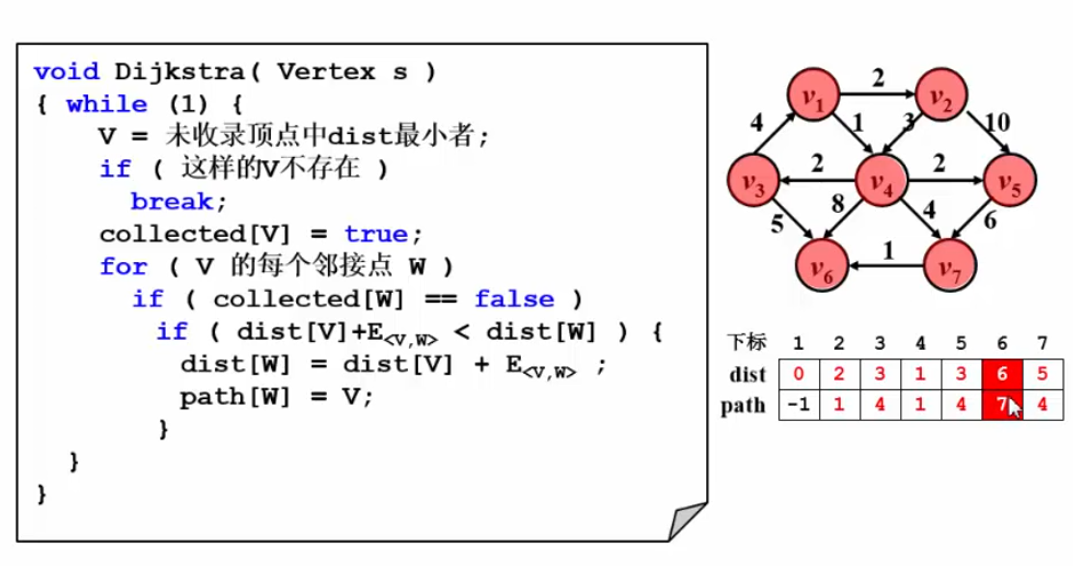
dijkstra算法的两个练习题：
6-11 Shortest Path [1]
6-12 Shortest Path [2]
最短路问题-Floyd算法
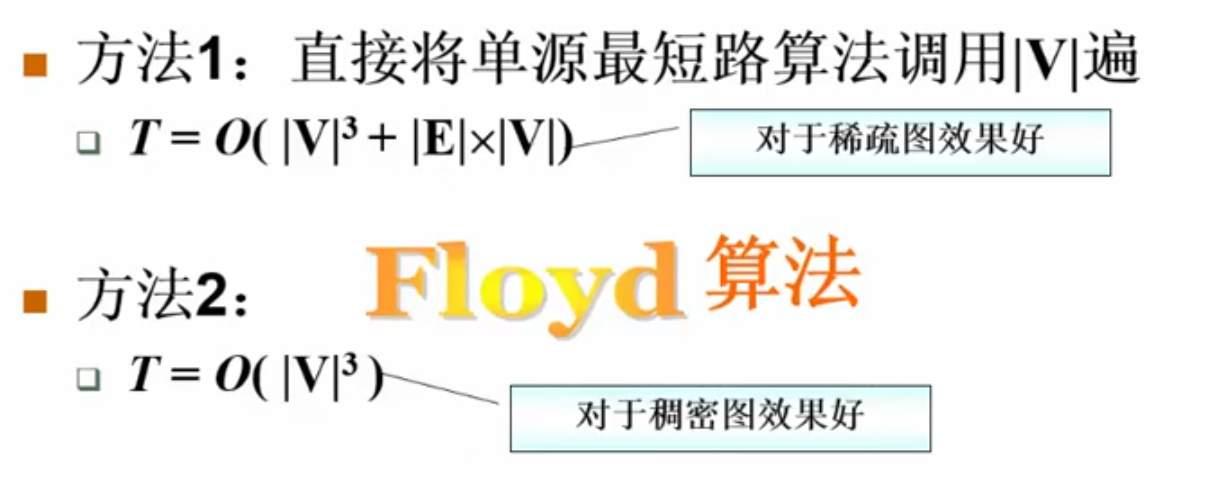
算法原理：
代码实现：
bool Floyd(MGraph Graph, WeightType D[MAXVERTEXNUM][MAXVERTEXNUM], Vertex[MAXVERTEXNUM][MAXVERTEXNUM]) {
Vertex i, j, k;
for (i = 0; i < Graph->Nv; ++i) {
for (j = 0; j < Graph->Nv; ++j) {
D[i][j] = Graph->G[i][j];
path[i][j] = -1;
}
}
for (k = 0; k < Graph->Nv; ++k) {
for (i = 0; i < Graph->Nv; ++i) {
for (j = 0; j < Graph->Nv; ++j) {
if (D[i][k] + D[k][j] < D[i][j]) {
D[i][j] = D[i][k] + D[k][j];
if (i == j && D[i][j] < 0)
return false;
path[i][j] = k;
}
}
}
}
return true;
}
时间复杂度：O(V^3)
哈利波特的考试
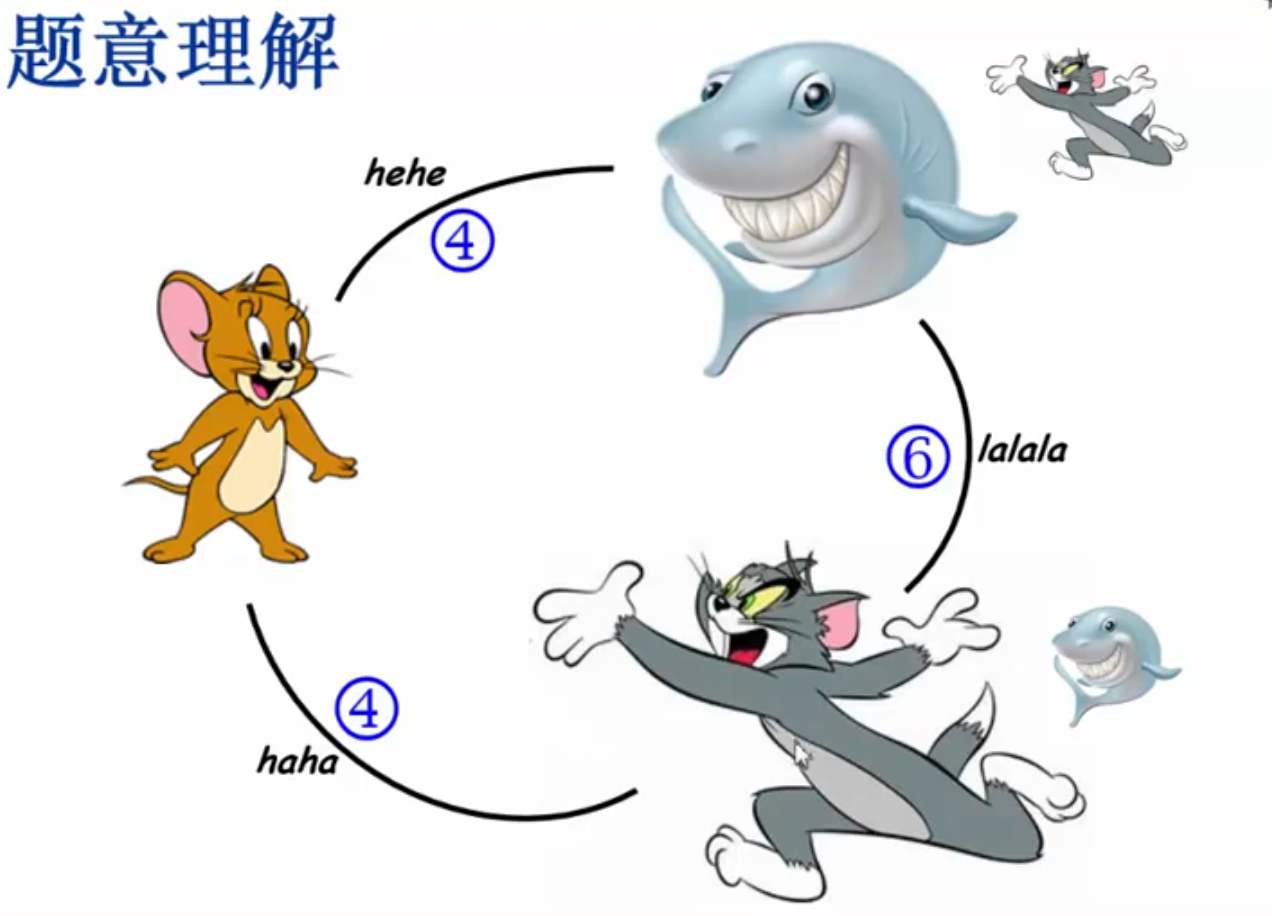
问题：带哪只动物去比较合算（咒语的长度最小）
题意理解：
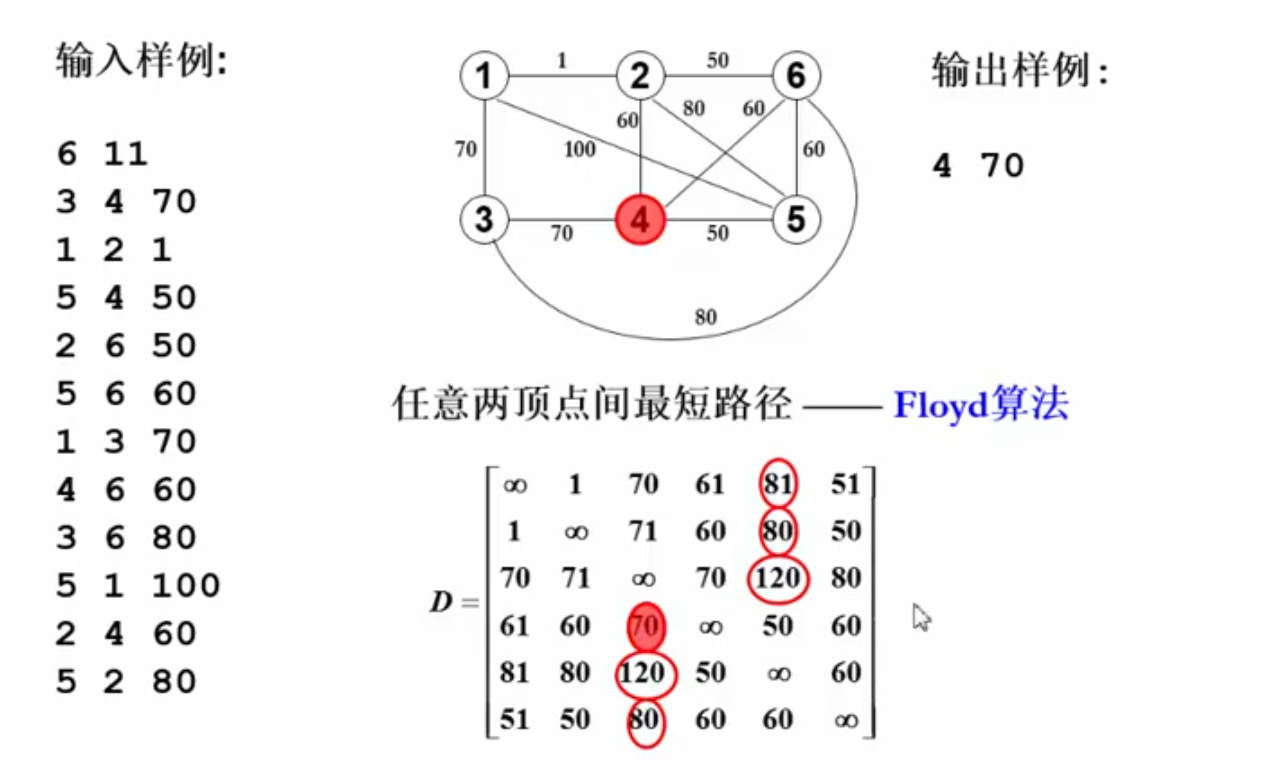
用Floyd算法求出任意两顶点之间的最短路，然后按行取每个顶点到其他顶点的最大值，最后取所有最大值的最小值（最好变的最难变的动物）
程序框架：
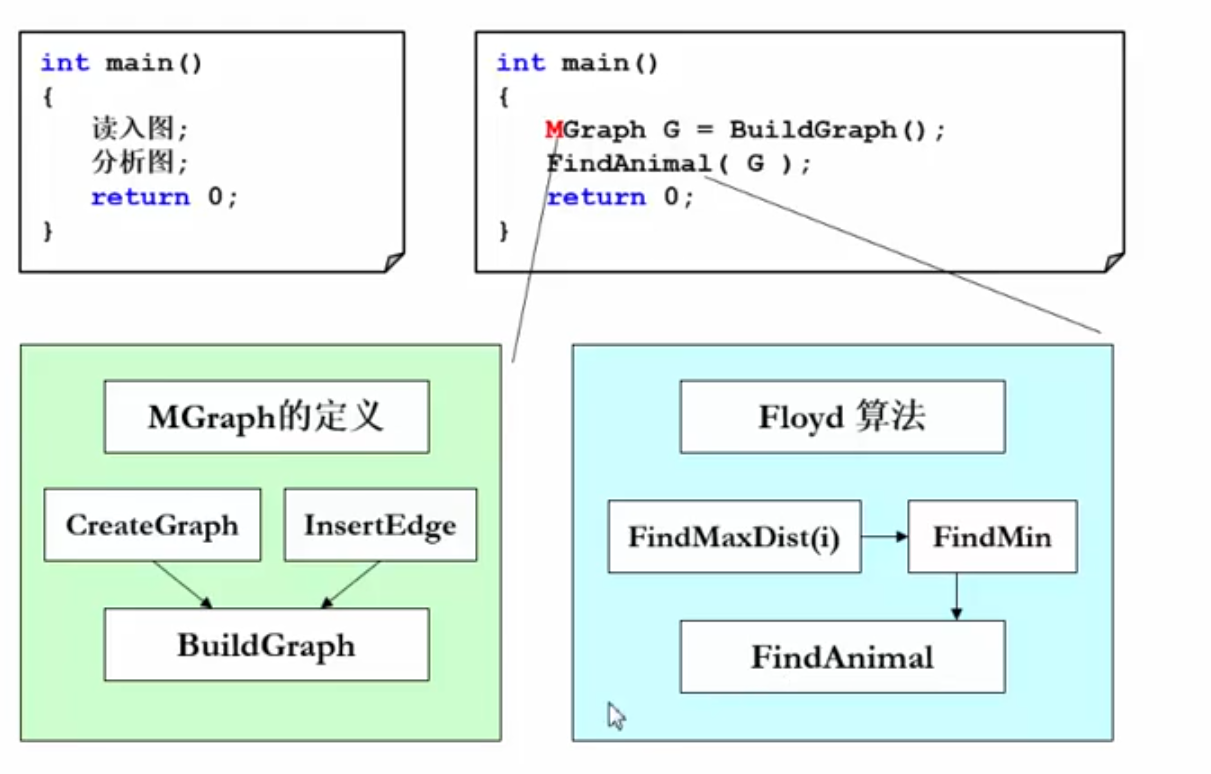
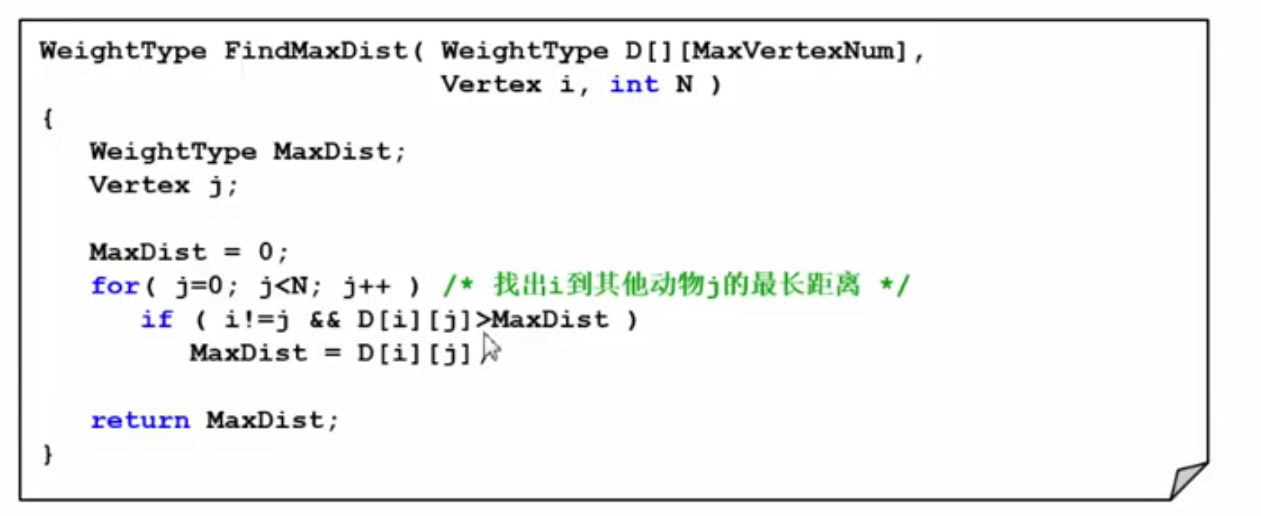
模块的引用与裁减：注意动物的编号从0开始
最小生成树问题-Prim算法
什么是最小生成树：
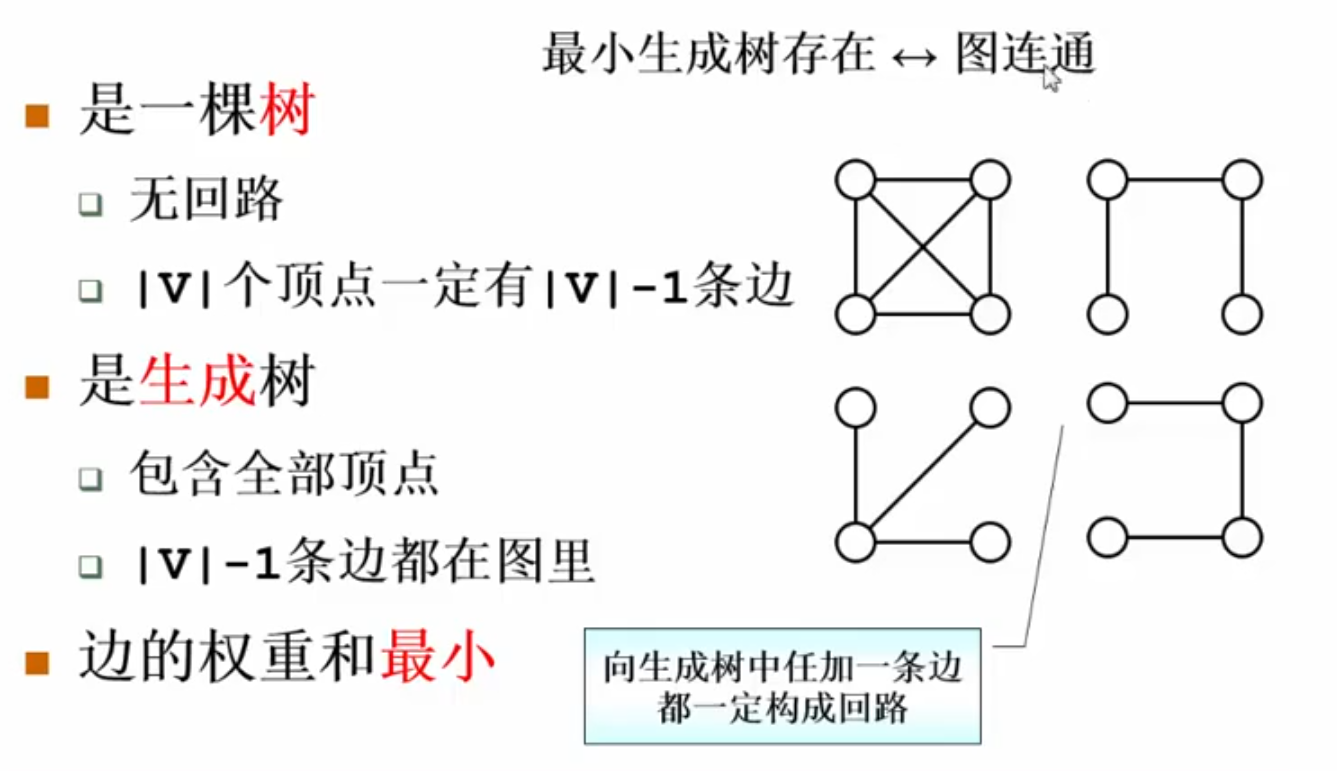
基于贪心算法：
Prim算法，让一棵小树长大：
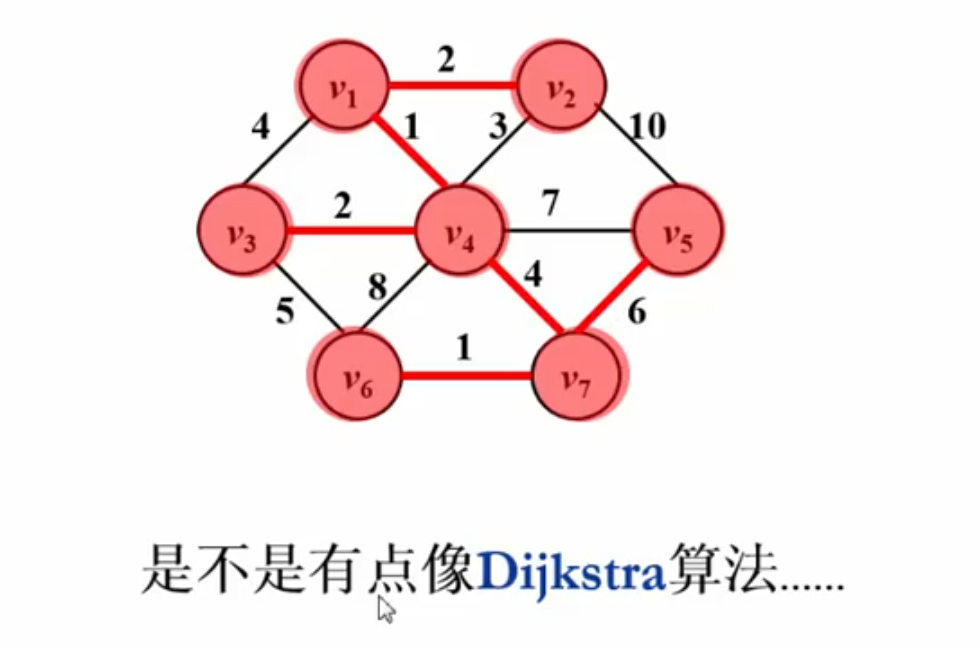
伪码描述：
代码实现：
//返回距离当前MST最近的顶点，若不存在返回-1
int find_closest_vertex(vector<int> &dist) {
int v = -1;
int mindist = X;
for (int i = 0; i < dist.size(); ++i) {
if (dist[i] != 0 && dist[i] < mindist) {
mindist = dist[i];
v = i;
}
}
return v;
}
/*
* 功能：求m的最小生成树，保存在mst中，并返回最小路径和
* 参数：m：待解图的邻接矩阵
* mst：传出的最小生成树，应保证与m的大小一致
* d：该图是否为有向图，若为无向图传false
* 返回值：成功返回最小路径和，若该图不连通，返回-1
* */
int Prim(const Mat &m, Mat &mst, bool d) {
int total_weight = 0;
int cnt = 0;
vector<int> dist(m[0]);
vector<int> parent(m.size(), 0);
dist[0] = 0;
parent[0] = -1;
cnt++;
while (1) {
int v = find_closest_vertex(dist);
if (v == -1)
break;
total_weight += dist[v];
mst[parent[v]][v] = dist[v];
if (!d)
mst[v][parent[v]] = dist[v];
dist[v] = 0;
cnt++;
for (int i = 0; i < m.size(); ++i) {
if (dist[i] != 0 && m[v][i] < X && m[v][i] < dist[i]) {
dist[i] = m[v][i];
parent[i] = v;
}
}
}
return cnt == m.size() ? total_weight : -1;
}
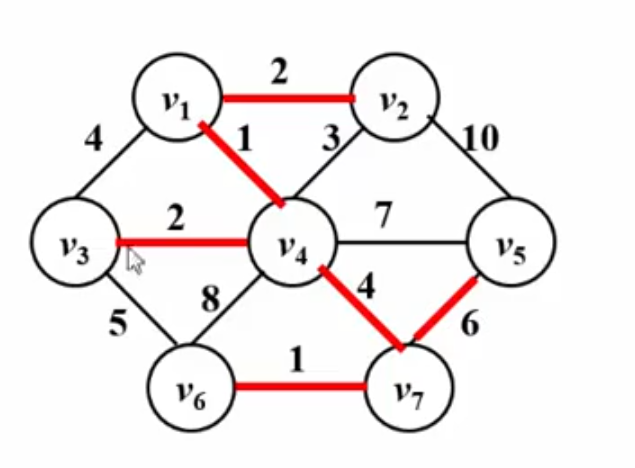
最小生成树问题-Kruskal算法
将初始的生成森林合并成树
伪码描述：
最小生成树的练习题：7-10 公路村村通
拓扑排序
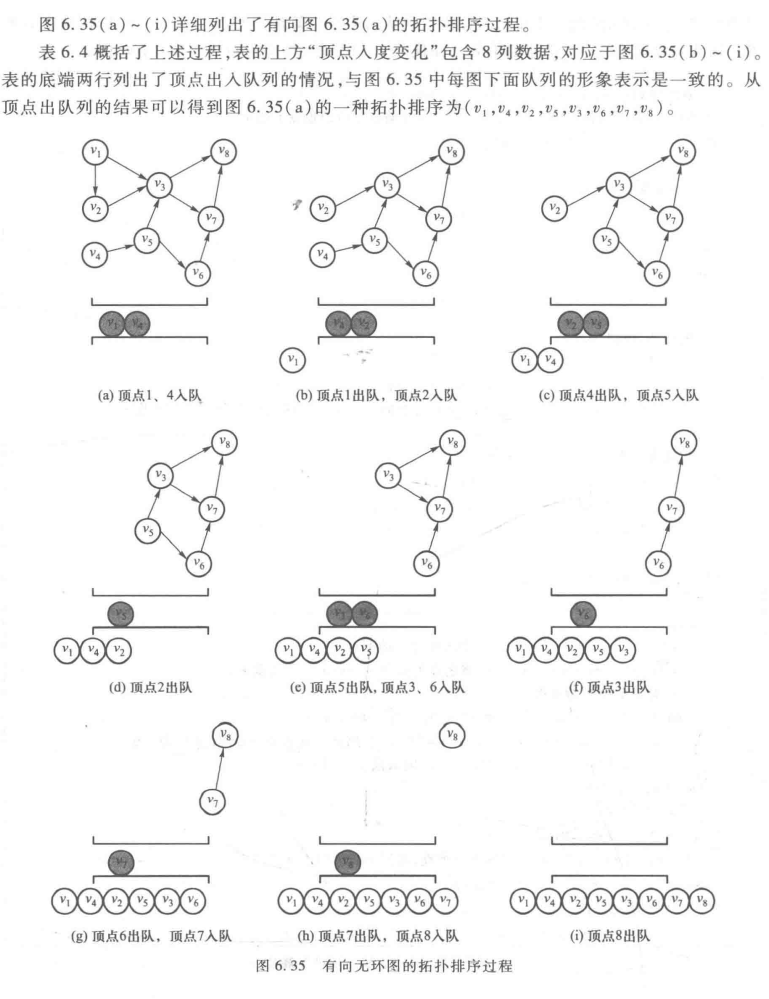
AOV网络：Activity On Vertex
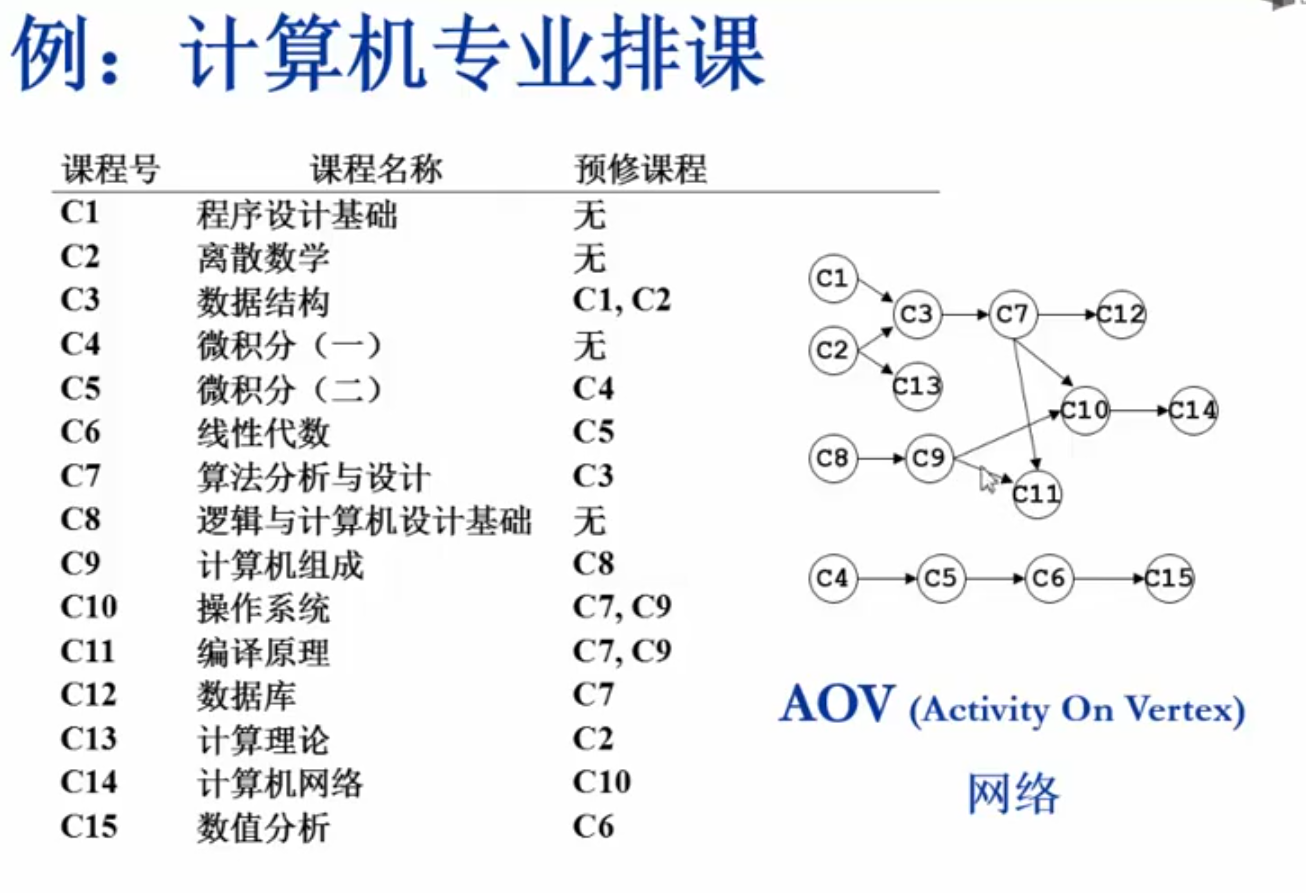
拓扑序：如果图中从V到W有一条有向路径，则V一定排在W之前。满足此条件的顶点序列称为一个拓扑序
获得一个拓扑序的过程就是拓扑排序
AOV如果有合理的拓扑序，则必定是有向无环图Directed Acyclic Graph,DAG
一个顶点数>1的有向图，如果每个顶点的入度都>0，那么它必定存在回路
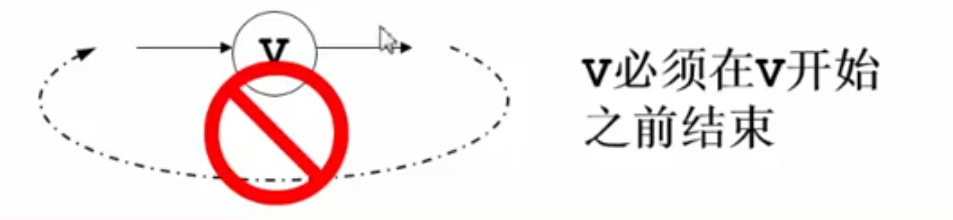
排序过程：分层次地，每次取出没有前驱节点的节点（InDegree==0）
伪码描述：
改进，采用队列，每次将入度变为0的顶点放在一个容器里：
算法实现：
//topological-sort.cpp
/*
* 功能：对有向图m进行拓扑排序，拓扑序列存储在top_order中
* 参数：m：待求解的有向图的邻接矩阵
* top_order：结果序列，传出参数
* 返回值：当前图是否有拓扑序列（如果有环则不存在拓扑序列，返回false）
* */
bool topological_sort(const Mat &m, vector<int> &top_order) {
int N = m.size();
vector<int> in_degree(N, 0);
top_order = vector<int>(N, -1);
//统计所有节点的入度
for (int i = 0; i < N; ++i) {
for (int j = 0; j < N; ++j) {
if (m[i][j] != 0 && m[i][j] != X) {
in_degree[j]++;
}
}
}
//将所有入度为0的节点压入队列q
queue<int> q;
for (int i = 0; i < N; ++i) {
if (in_degree[i] == 0) {
q.push(i);
}
}
int cnt = 0;
while (!q.empty()) {
int t = q.front();
q.pop();
top_order[cnt++] = t; //取出队头元素t加入拓扑序列
for (int i = 0; i < N; ++i) {
if (m[t][i] != 0 && m[t][i] != X) {
in_degree[i]--; //对于每个被t指向的节点，入读--；如果被减为0，加入队列q
if (in_degree[i] == 0) {
q.push(i);
}
}
}
}
return cnt == N; //若没有把所有节点都统计在内，说明有环，无拓扑序列
}
拓扑排序算法还可以用来检测一个有向图是否是DAG
拓扑排序过程的一个实例：
关键路径
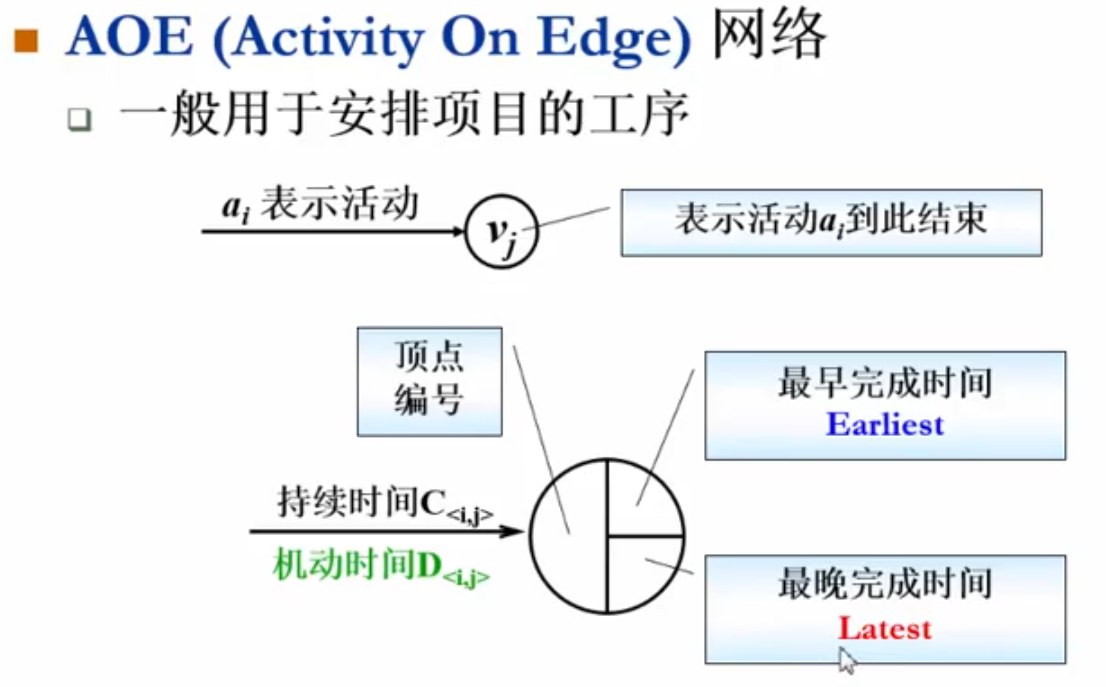
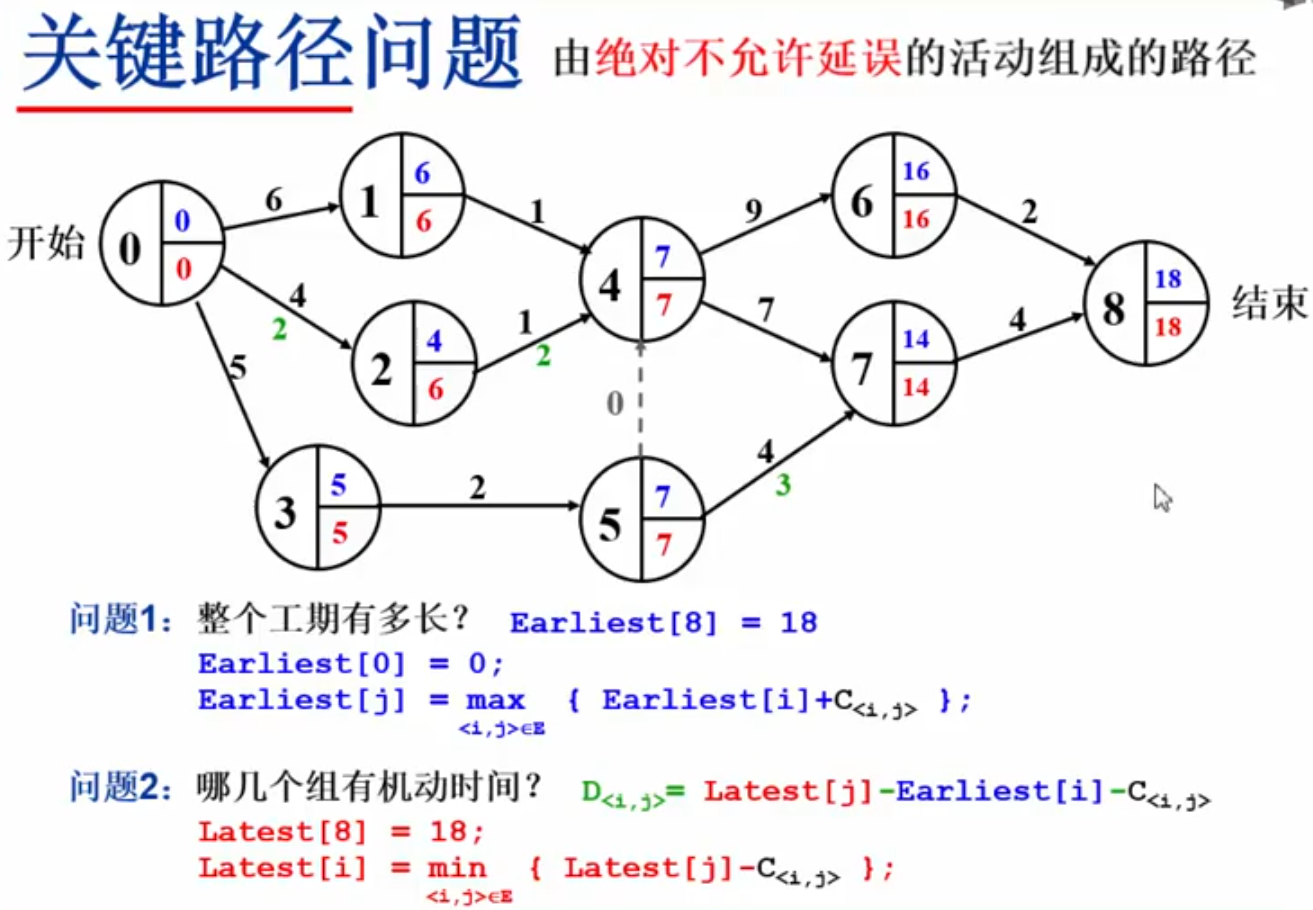
Activity On Edge，AOE网络：
旅游规划
在距离最短的前提下寻找收费最少的路径（多关键字的最短路径问题）
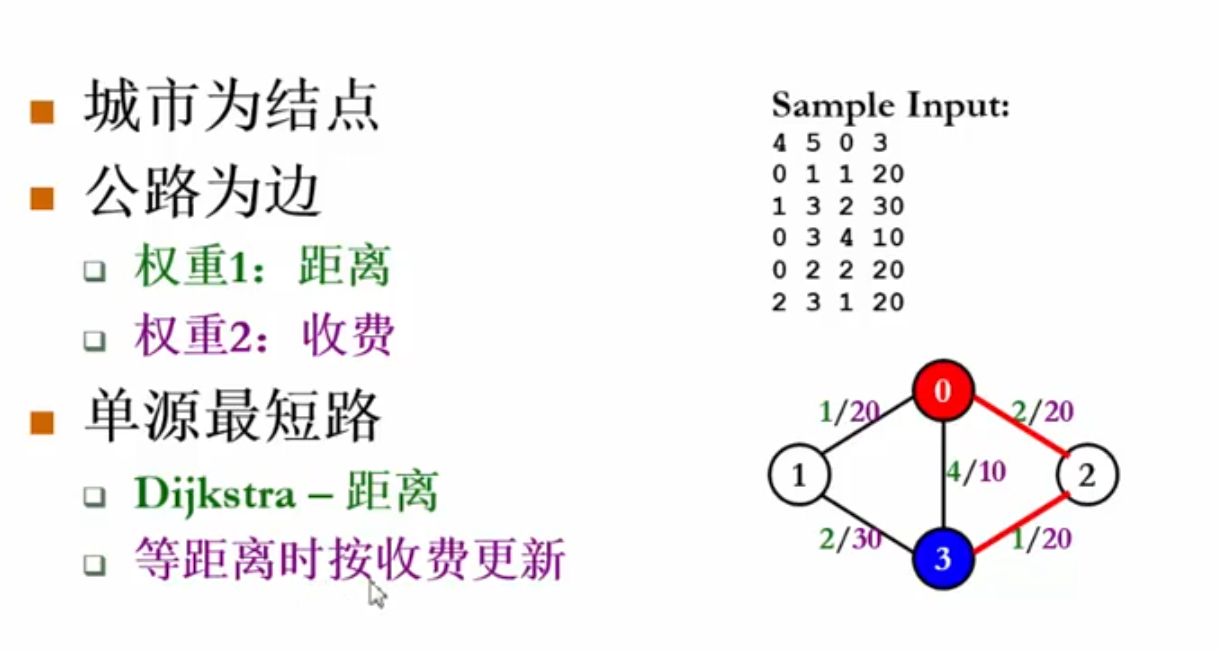
算法伪码描述：与原始的Dijsktra算法不同的是，我们需要记录一个cost，当最短路被更新时，cost也要被更新。同时，如果找到了距离相等的路径，还要检查cost是否更小，如果更小，也要更新cost和path数组
其他类似问题：count[v]记录从原点到v点的路径有多少条
找到边数最少的最短路与上面的”旅游规划“问题等价，只不过所有边的cost都是1
1976. 到达目的地的方案数
五、排序
接口规范：
void x_sort(vector<int>& A);
为简单起见，只讨论从小到大的整数排序，而且约定：
- N是正整数；
- 只讨论基于比较的排序（>,=,<有定义）；
- 只讨论内部排序；
稳定性：任意两个相等的数据，排序前后的相对位置不发生改变
注意：没有一种排序算法在任何情况下都表现最好，它们各有所长
力扣排序算法练习：912. 排序数组
冒泡排序
void bubble_sort(vector<int> &A) {
bool sorted = false;
int N = A.size();
while (!sorted) {
sorted = true;
for (int i = 1; i < N; ++i) {
if (A[i - 1] > A[i]) {
swap(A[i - 1], A[i]);
sorted = false;
}
}
N--;
}
}
The best time complexity=O(n)
The worst time complexity=O(n^2)
Space complexity=O(1)
冒泡排序算法是稳定的
插入排序
算法思路：一维数组被分为前后两部分：已排序部分和未排序部分。初始时将待排序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
然后从头到尾依次扫描未排序序列for (p = 1; p < N; ++p)，取出未排序部分的第一个元素到tmp，并将tmp插入到前面有序序列的适当位置：i从p开始，只要i > 0 && tmp < A[i - 1]，就不断地将A[i-1]向后移动 A[i] = A[i - 1];。
跳出内层for循环时，说明tmp已经找到了合适的位置，将其插入A[i] = tmp;。
可见插入排序对于链表是比较方便的，数组还要不断的挪动空间。
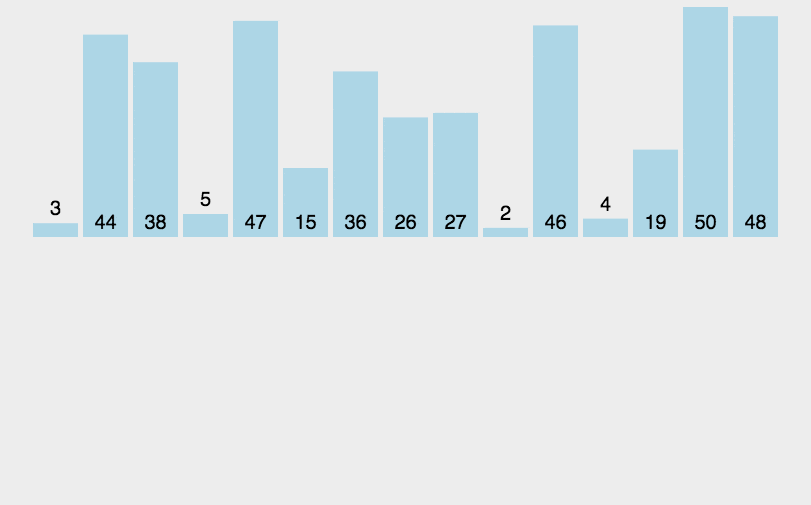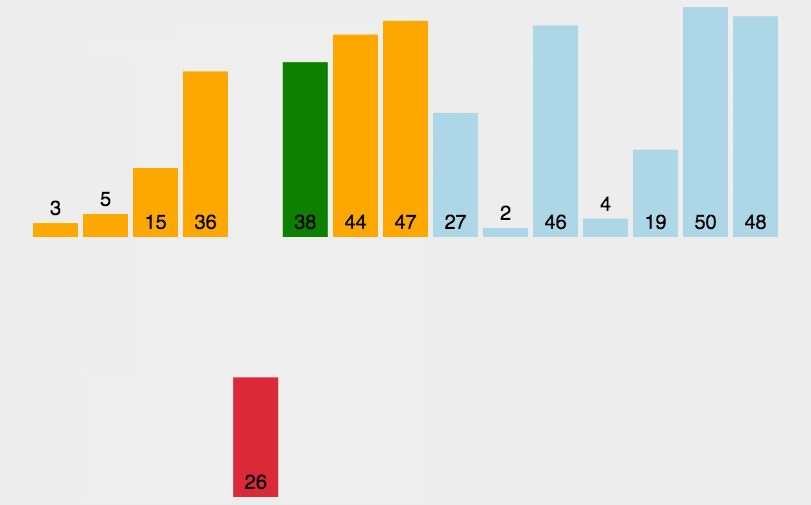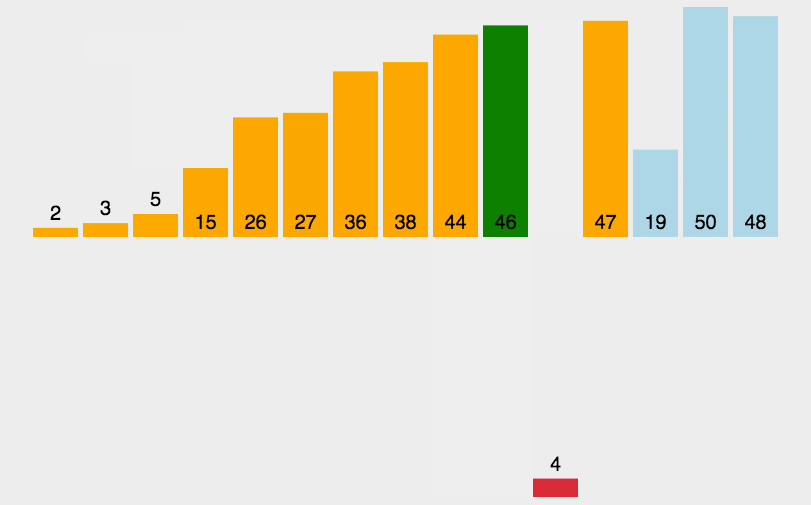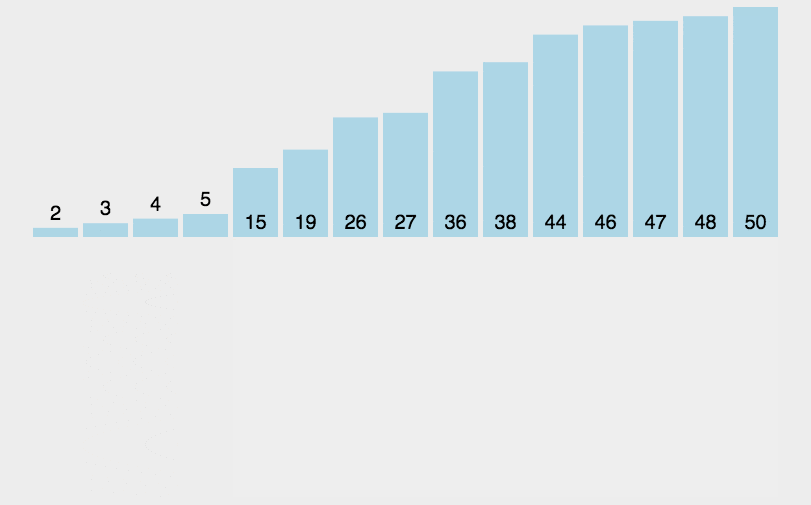
void insertion_sort(vector<int> &A) {
int t = 0, i, j;
for (i = 1; i < A.size(); ++i) {
//外层循环每次取未排序部分的首个元素
t = A[i];
//从排好序的最后一个元素开始向前比较，只要tmp小，就将元素向后移
for (j = i; j > 0 && A[j - 1] > t; --j) {
A[j] = A[j - 1];
}
A[j] = t;
}
}
The best time complexity=O(n)
The worst time complexity=O(n^2)
Space complexity=O(1)
时间复杂度下界：
交换两个相邻元素正好消去一对逆序对
插入排序的时间复杂度：T(N,I)=O(N+I)，既取决于N又取决于I，所以如果一个序列基本有序，那么插入排序就简单高效
定理：任意N个不同元素组成的序列平均具有 N ∗ ( N − 1 ) / 4 N*(N-1)/4 N∗(N−1)/4个逆序对
定理：任何仅以交换相邻两元素来排序的算法，时间复杂度下界为O(N^2)
所以为了提高算法效率，必须采用如下的改进方案：
- 每次消去不止1个逆序对
- 每次交换相隔较远的2个元素
希尔排序
按照增量序列，先进行5间隔排序，再进行3间隔排序，最后进行1间隔排序
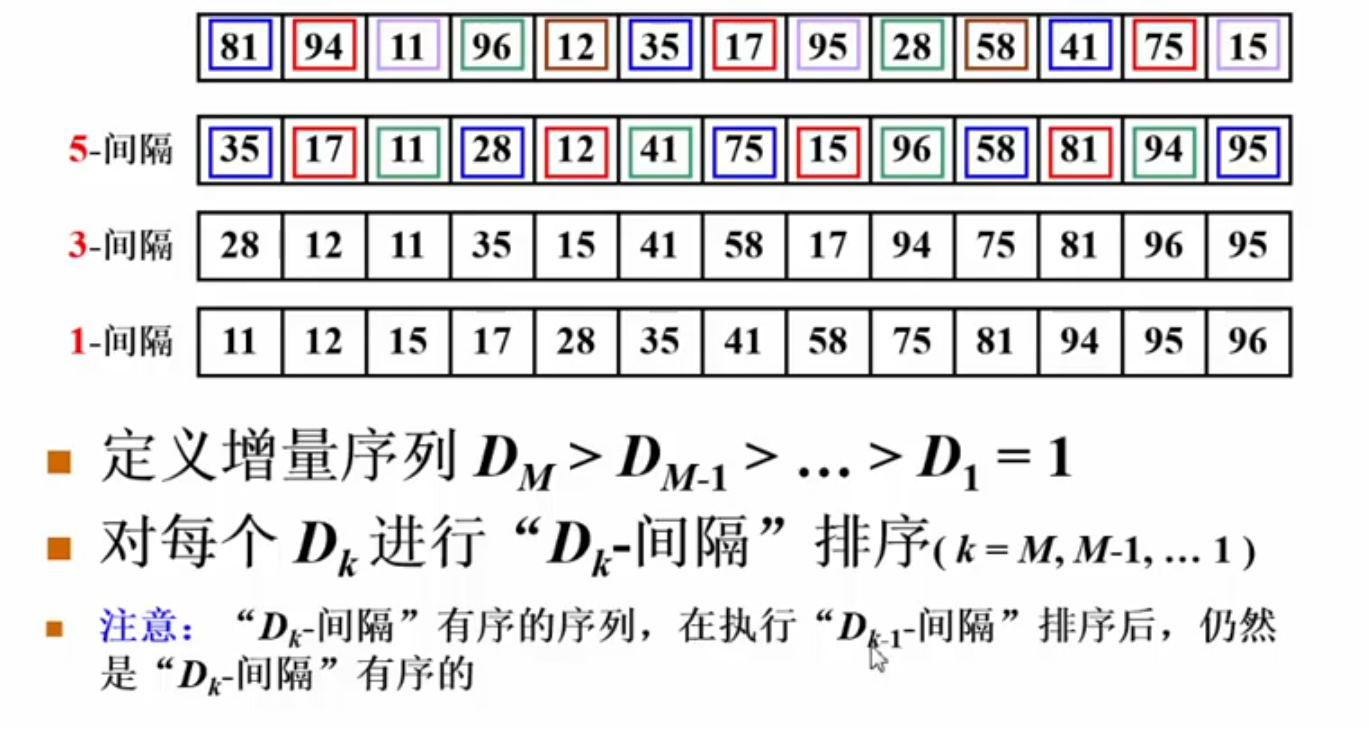
希尔排序作为插入排序的一种改进，其时间复杂度有所优化，但希尔排序是不稳定的
原理概述：将无序数组分割为若干个子序列，子序列不是逐段分割的，而是相隔特定的增量的子序列，对各个子序列进行插入排序；然后再选择一个更小的增量，再将数组分割为多个子序列进行排序。最后选择增量为1，即使用直接插入排序，使最终数组成为有序
希尔排序的效果与选用的增量序列有关，效果比较好的是Sedgewick增量序列，这里为了简单起见这里我们用N/2,N/4……来充当增量序列
举例来说，我们有下面10个待排数据，利用for循环for (D = N >> 1; D > 0; D >>= 1) 产生增量序列。首先进行D=5间隔的插入排序：
p指向增量序列的下一个元素，取到tmp中，然后向前执行插入排序，只不过把原来插入排序-1的地方都换成了-D，表示D间隔的插入排序
然后同理进行2间隔的插入排序，最后进行1间隔的插入排序，也就是传统的插入排序，但是由于序列此时已经基本有序，执行起来要快得多
void shell_sort(vector<int> &A) {
int d, i, j, t;
for (d = A.size() / 2; d > 0; d /= 2) {
for (i = d; i < A.size(); ++i) {
t = A[i];
for (j = i; j >= d && t < A[j - d]; j -= d) {
A[j] = A[j - d];
}
A[j] = t;
}
}
}
- The best time complexity≈O(n^1.3)
- The worst time complexity=O(n^2)
- Space complexity=O(1)
其最好时间复杂度和平均时间复杂度与选用的增量序列有关，精确的表达式在数学上尚未得到解决
增量序列至关重要：
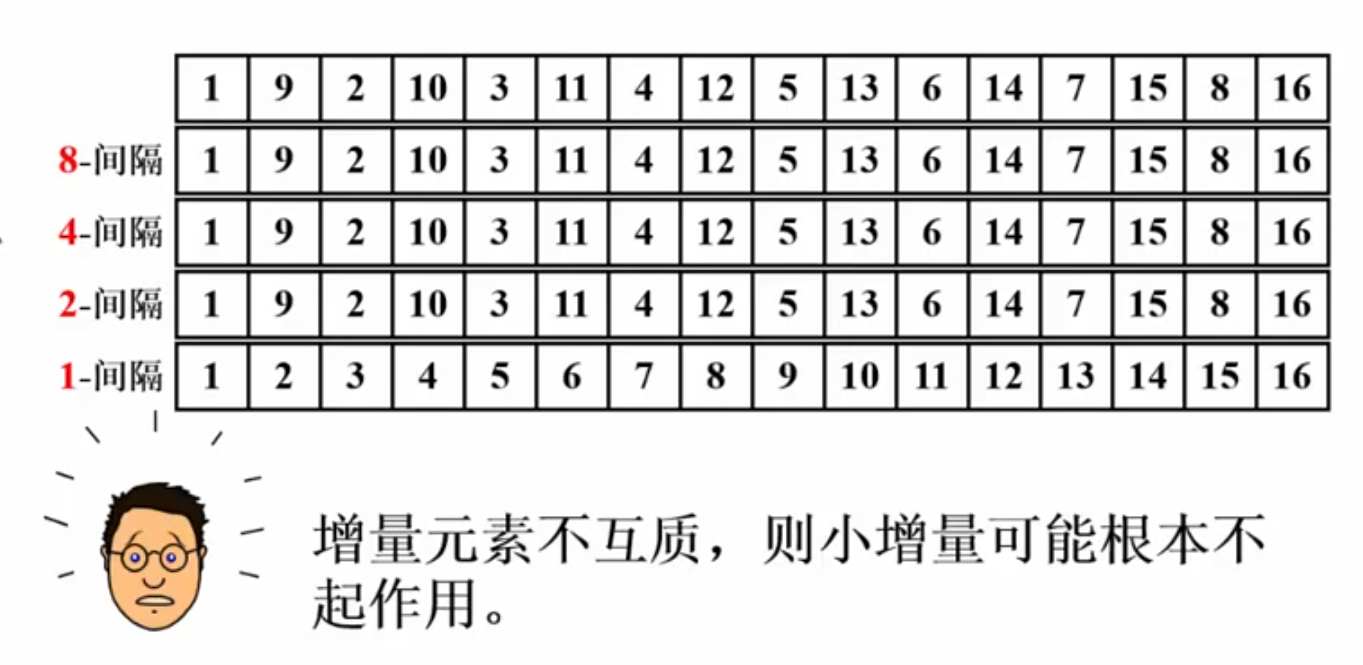
不同的增量序列会带来不同的时间复杂度：
希尔排序适合数目较大（几万~几十万）的排序，搭配Sedgewick增量序列
选择排序
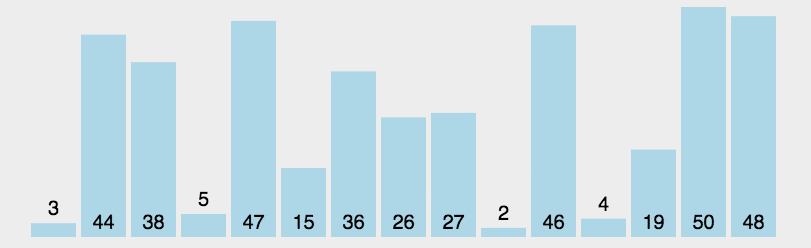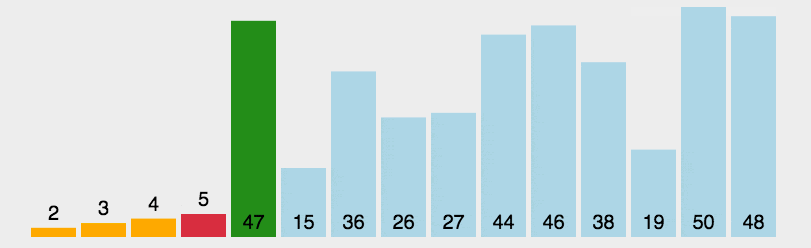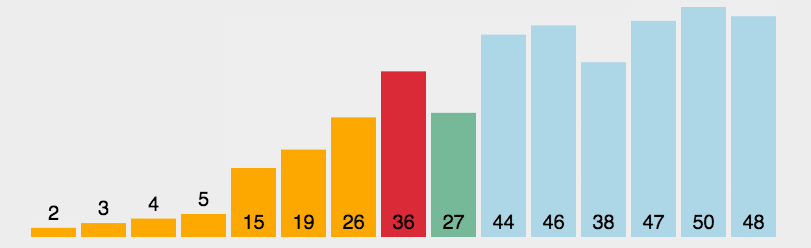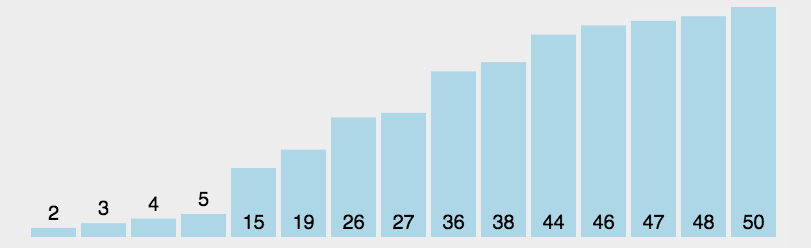
每次都从后面的未排序部分选取一个最小元素，然后换到前面已排序后面的最后位置
代码实现：
static int scan_for_min(vector<int>& A, int l, int r) {
int min = A[l];
int minpos = l;
for (int i = l; i <= r; ++i) {
if (A[i] < min) {
min = A[i];
minpos = i;
}
}
return minpos;
}
void selection_sort(vector<int>& A) {
int minpos = 0;
int N = A.size();
for (int i = 0; i < N; ++i) {
minpos = scan_for_min(A, i, N - 1);
swap(A[i], A[minpos]);
}
}
时间复杂度：稳定的 Θ ( N 2 ) Theta(N^2) Θ(N2)
如何更快速找到最小元：借助小顶堆
堆排序
堆排序是对选择排序的改进。由上面选择排序的分析可知，其时间复杂度无论如何都是稳定的O(n^2)，关键在于scan_for_min的时间复杂度太高，达到了O(n)，而堆排序就是利用大顶堆将scan_for_min的过程优化为了O(logn)
对于原始序列：
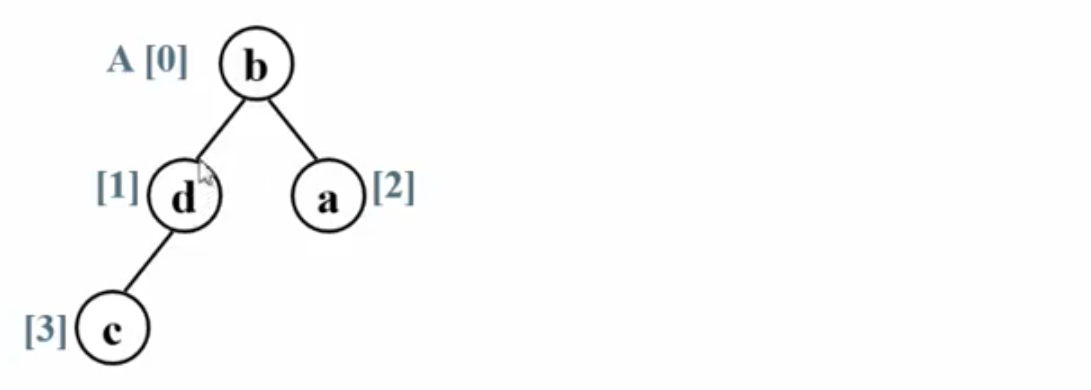
首先将他调整为大顶堆：
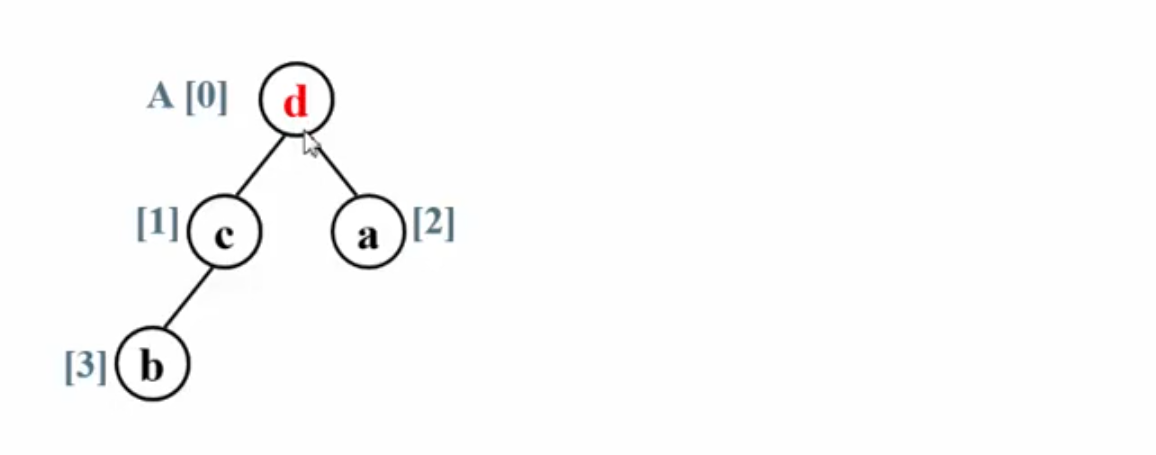
此时堆顶已经是最大元素，根据从小到大的排序要求，将他和最后一个元素交换，这样，数组的后面就部分有序了，待排序的数组规模减一：
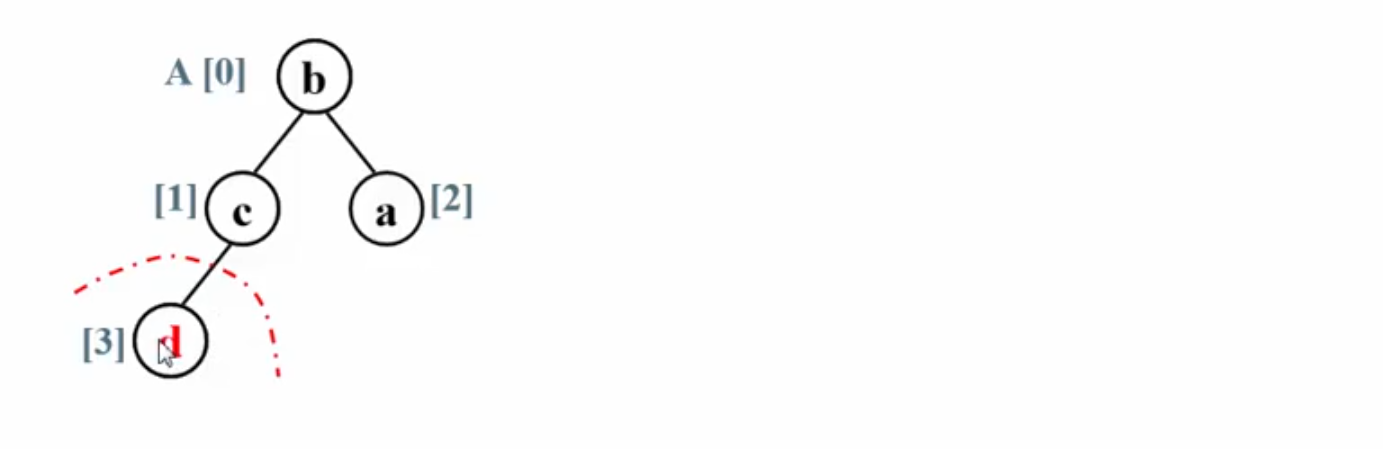
再将剩下的三个节点调整为大顶堆：
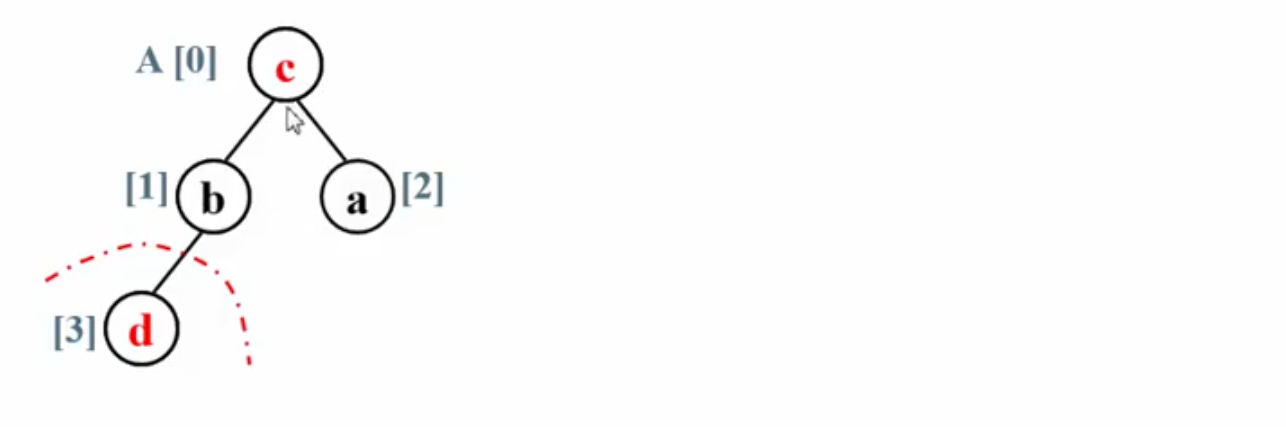
重复之前的步骤，这样不断进行下去，最终序列有序
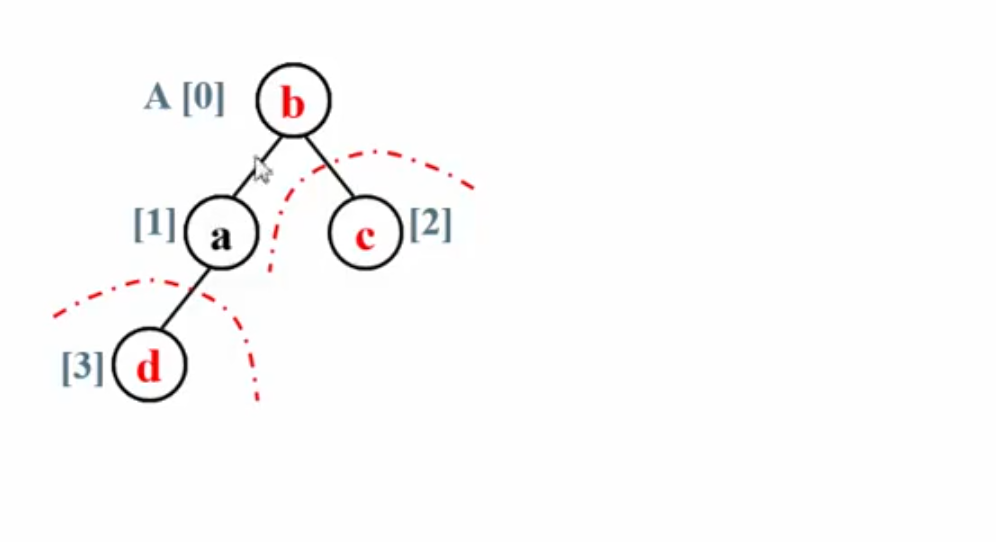
下面的动画很好地演示的堆排序的过程：
static void perc_down(vector<int> &A, int i, int N) {
int parent = i;
int child;
int top = A[i];
for (; parent * 2 + 1 < N; parent = child) {
child = parent * 2 + 1;
if (child < N - 1 && A[child + 1] > A[child]) {
child++;
}
if (top >= A[child]) {
break;
} else {
A[parent] = A[child];
}
}
A[parent] = top;
}
void heap_sort(vector<int> &A) {
int N = A.size();
for (int i = N / 2; i >= 0; --i) {
perc_down(A, i, N);
}
for (int i = N - 1; i > 0; --i) {
swap(A[i], A[0]);
perc_down(A, 0, i);
}
}
最好和最坏的时间复杂度都是 O ( n ∗ l o g n ) O(n*logn) O(n∗logn)
定理：堆排序处理N个不同元素的随机排列的平均比较次数是 2 N ∗ l o g N − O ( N ∗ l o g l o g N ) 2N*logN-O(N*loglogN) 2N∗logN−O(N∗loglogN)
虽然堆排序给出最佳平均时间复杂度，但实际效果不如用Sedgewick增量序列的希尔排序
归并排序-递归算法
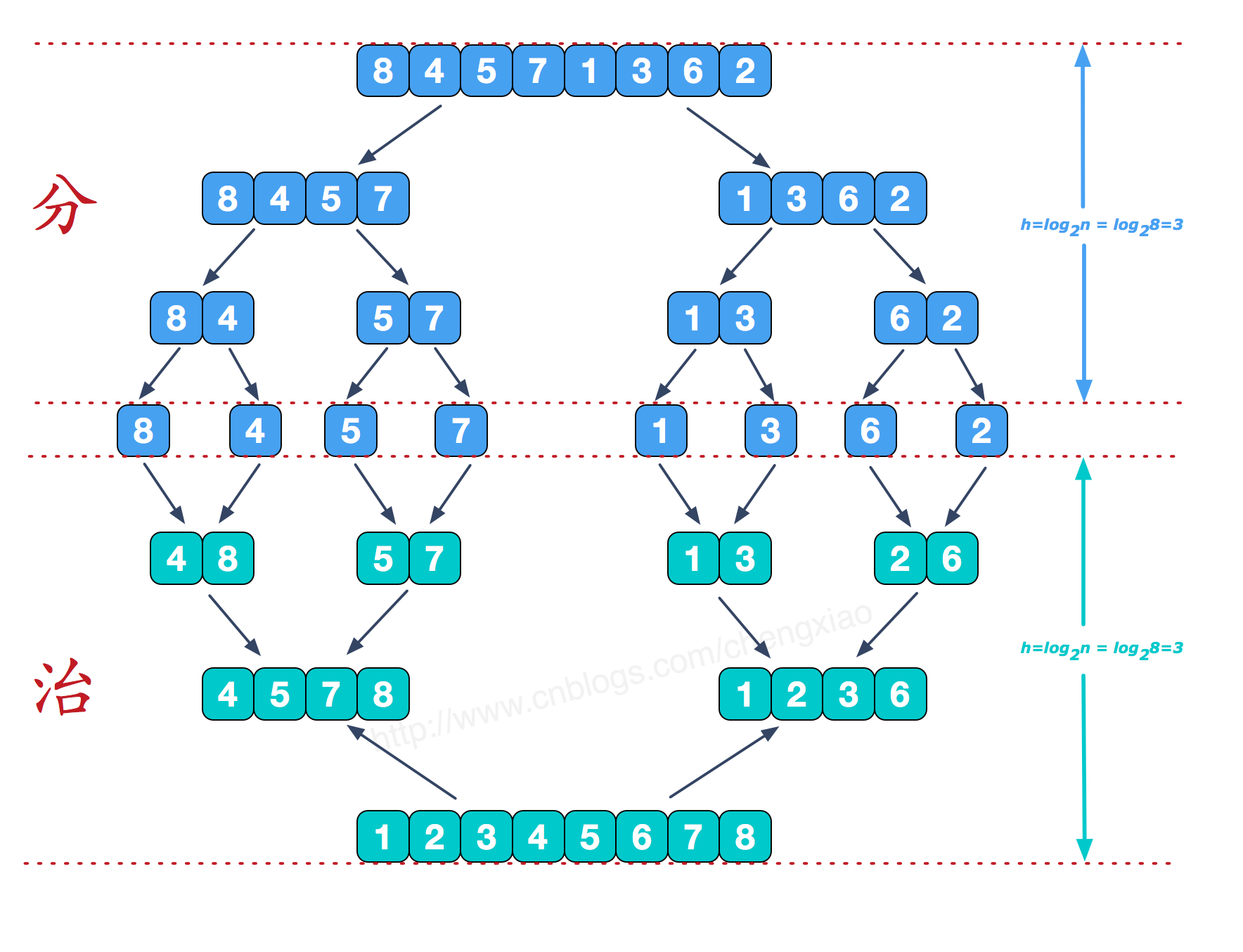
递归版本的归并排序采用分而治之的策略，每次求出待排序列的中点int mid = (low + high) / 2;，然后递归地解决左半边，再递归地解决右半边，最后将从low到mid和从mid+1到high的两个子列进行归并，递归终点是if (low < high)
下面的动画很好地演示了归并排序递归返回的过程：
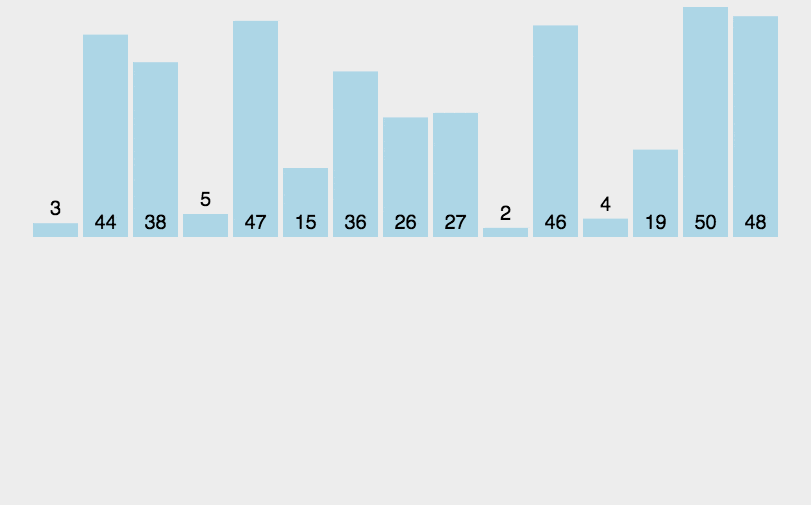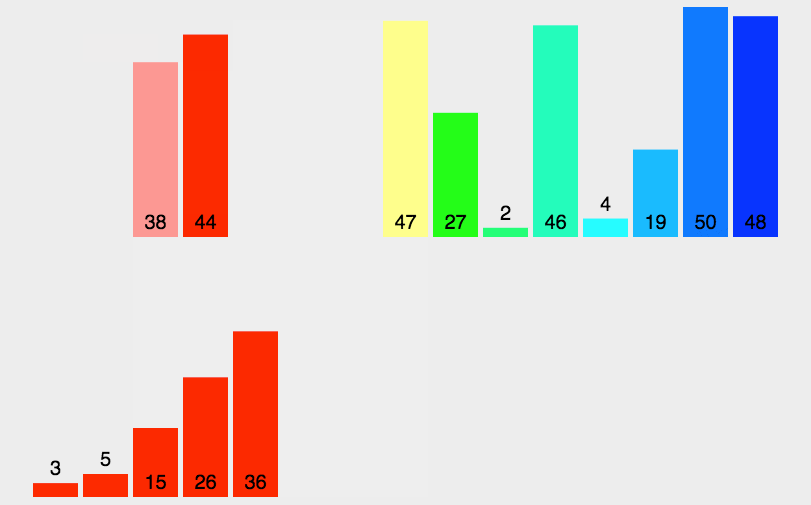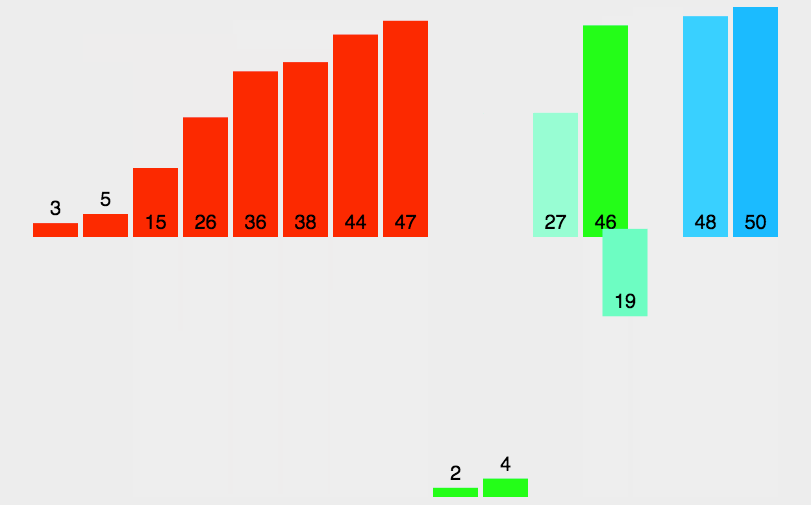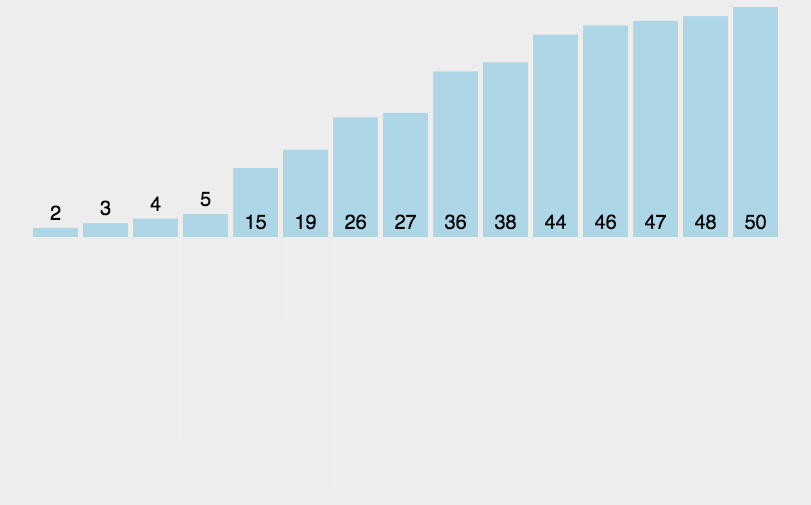
归并的时间复杂度为O(n)
归并的代码实现：
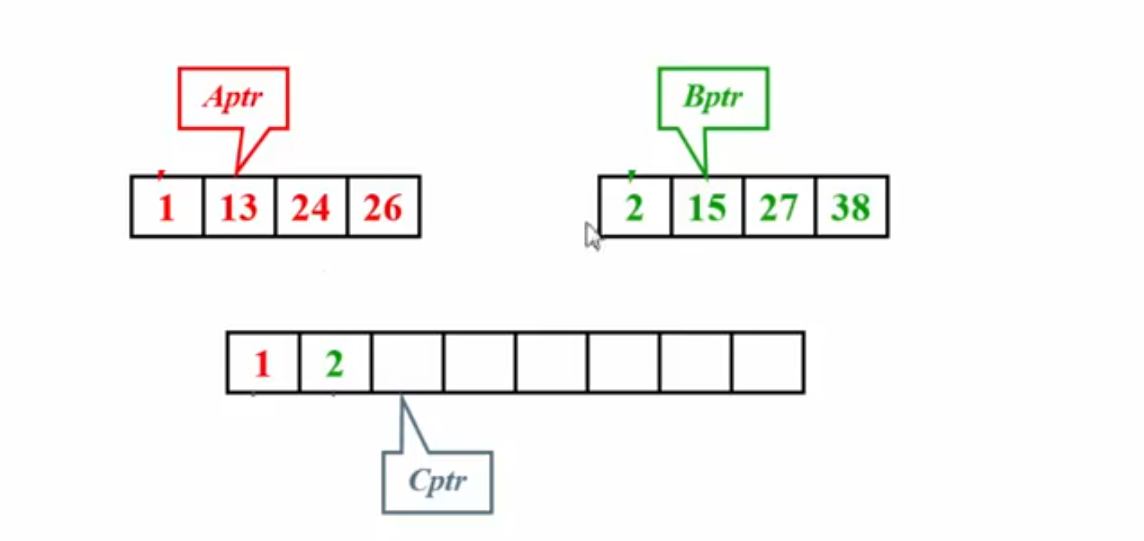
static void merge(vector<int> &A, int low, int mid, int high) {
vector<int>::iterator it = A.begin();
vector<int> L(it + low, it + mid + 1);
vector<int> R(it + mid + 1, it + high + 1);
int i = 0, j = 0, k = low;
for (; i < L.size() && j < R.size();) {
if (L[i] <= R[j]) {
A[k++] = L[i++];
} else {
A[k++] = R[j++];
}
}
while (i < L.size()) A[k++] = L[i++];
while (j < R.size()) A[k++] = R[j++];
}
代码实现：
static void _merge_sort(vector<int> &A, int low, int high) {
if (low < high) {
int mid = (low + high) / 2;
_merge_sort(A, low, mid);
_merge_sort(A, mid + 1, high);
merge(A, low, mid, high);
}
}
时间复杂度： O ( n ∗ l o g n ) O(n*logn) O(n∗logn)，无论好坏
为了统一函数接口：
void merge_sort(vector<int> &A) {
_merge_sort(A, 0, A.size() - 1);
}
归并排序-非递归算法
首先将相邻的两个子序列做归并；
再归并两个相邻的子序列，以此类推，这样以二倍的递归排序，但是需要不断的开辟空间，造成了O(n*logn)的空间复杂度：
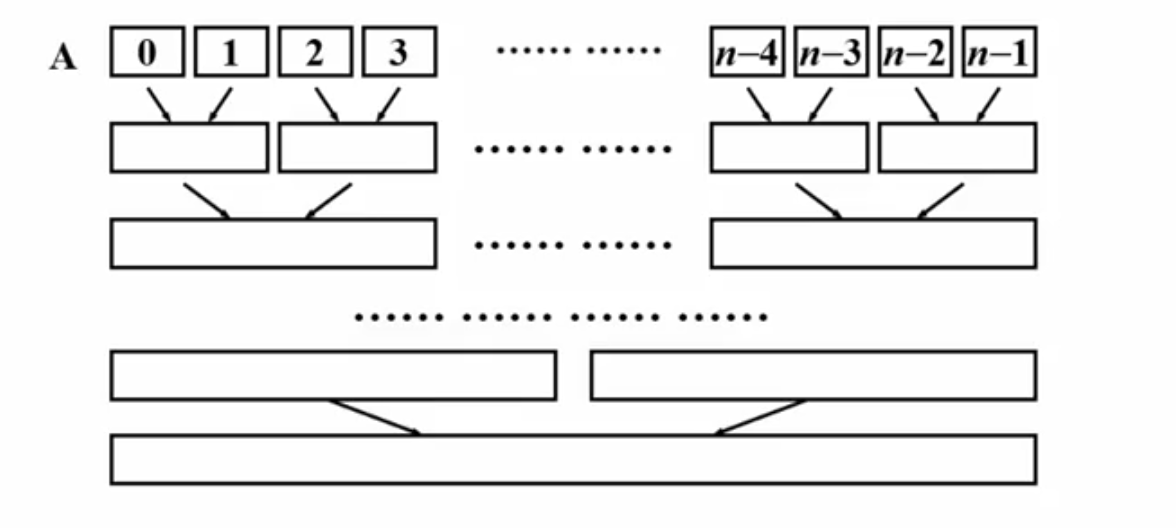
其实不用一直开辟空间，可以只开辟一个辅助数组，在原数组A和辅助数组TmpA中来回归并折腾，这样的空间复杂度为O(n)。
在一趟length间隔的归并排序中，反复调用Mere_simple，将A归并排序到TempA中，最后需要根据剩余元素的数量决定是否还够一趟归并的，代码实现如下：
static void Merge_pass(ElementType A[], ElementType TempA[], int N, int length) {
int i, j;
for (i = 0; i < N - 2 * length; i += 2 * length) {
Merge_simple(A, TempA, i, i + length, i + 2 * length - 1);
}
if (i + length < N) {
Merge_simple(A, TempA, i, i + length, N - 1);
} else {
for (j = i; j < N; ++j)
TempA[j] = A[j];
}
return;
}
其中Merge_simple就是将A中的元素归并排序到TempA中，不像上面的实现方式，这里不需要倒回元素，其代码实现如下：
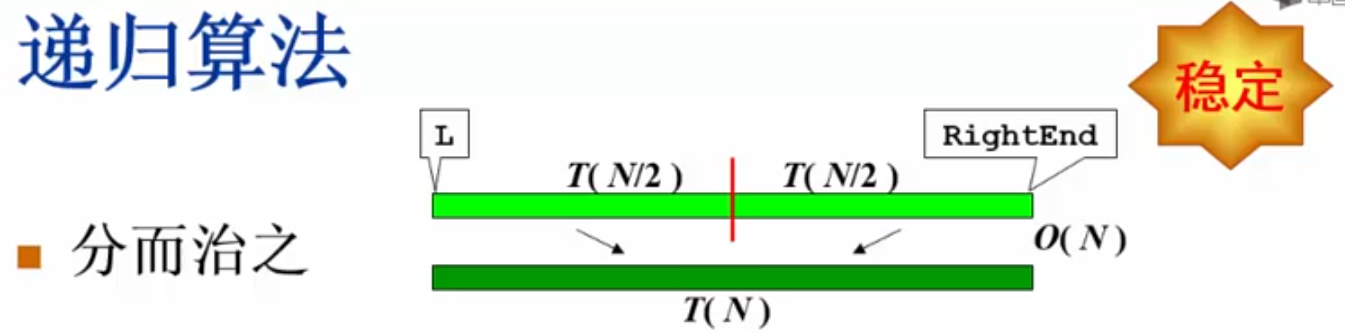
static void Merge_simple(ElementType A[], ElementType TempA[], int L, int R, int RightEnd) {
int LeftEnd = R - 1;
int Tmp = L;
while (L <= LeftEnd && R <= RightEnd) {
if (A[L] <= A[R]) {
TempA[Tmp++] = A[L++];
} else {
TempA[Tmp++] = A[R++];
}
}
while (L <= LeftEnd)
TempA[Tmp++] = A[L++];
while (R <= RightEnd)
TempA[Tmp++] = A[R++];
return;
}
最终的归并排序接口：
void Merge_Sort_iteratively(ElementType A[], int N) {
printf("%s:", __func__);
int length = 1;
ElementType* TempA = (ElementType*)malloc(N * sizeof(ElementType));
if (TempA != NULL) {
while (length < N) {
Merge_pass(A, TempA, N, length);
length *= 2;
Merge_pass(TempA, A, N, length);
length *= 2;
}
free(TempA);
} else {
printf("空间不足n");
}
return;
}
归并排序是稳定的，但是一般不用作内部排序，用做外排序非常有用
快速排序
快速排序比较适合进行随机数据的排序
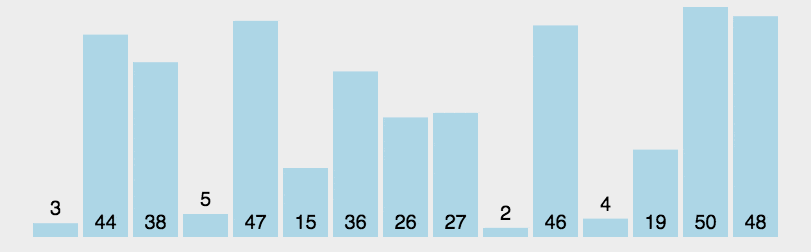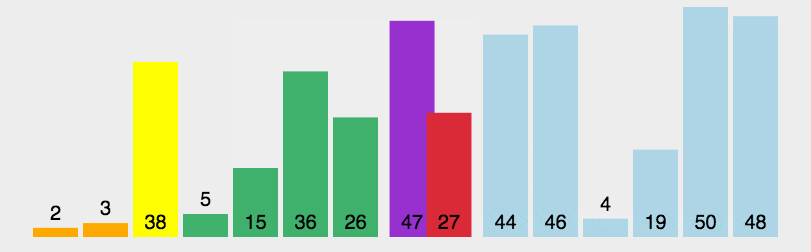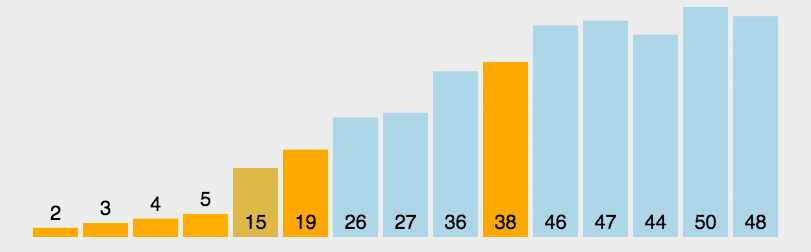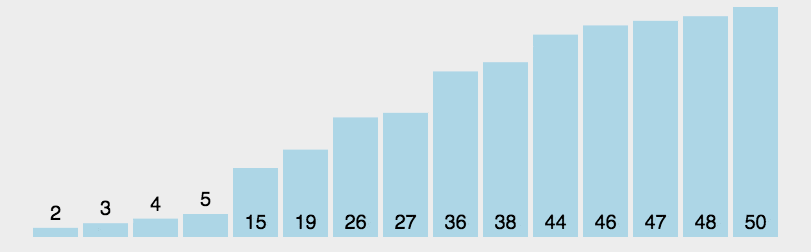
依然采用分而治之的思想：
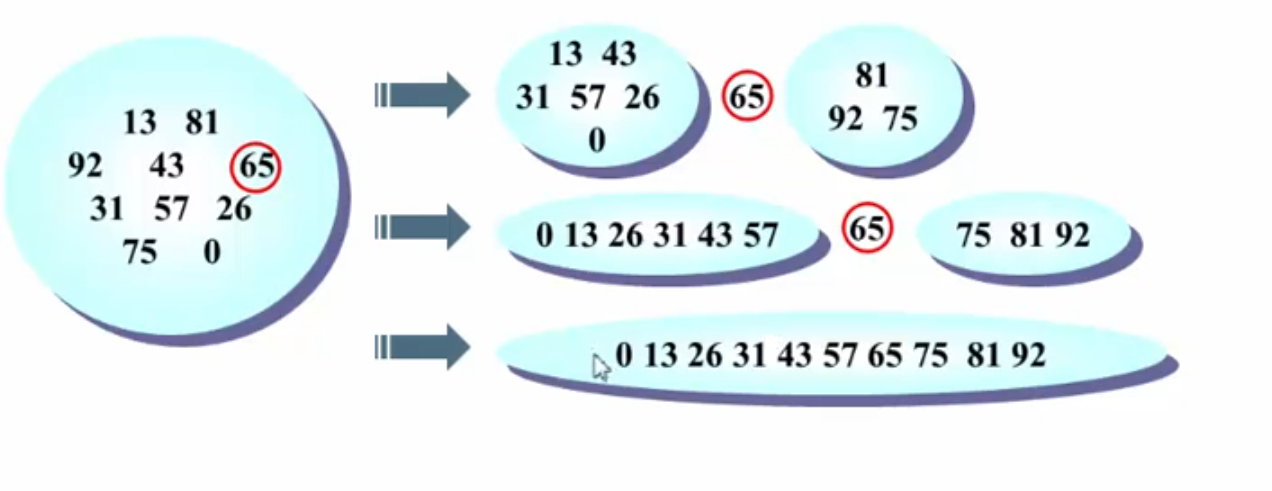
选择65作为主元，将集合分为左右两部分，然后递归的将左边排序，再递归的将右边排序，最后合并结果
算法概述：
-
从数列中挑出一个元素，称为 “基准”（pivot）
-
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作
-
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序
快速排序的基本实现：
static int partition(vector<int> &A, int left, int right) {
int pivot = A[left];
while (left < right) {
while (left < right && A[right] >= pivot) right--;
A[left] = A[right];
while (left < right && A[left] <= pivot) left++;
A[right] = A[left];
}
A[left] = pivot;
return left;
}
/**另一种划分方式**/
static int partition2(vector<int> &A, int low, int high) {
int pivot = A[high];
int i = low - 1;
for (int j = low; j < high; ++j) {
if (A[j] <= pivot) {
swap(A[++i], A[j]);
}
}
swap(A[++i], A[high]);
return i;
}
static void _quick_sort(vector<int> &A, int left, int right) {
if (left < right) {
int p = partition(A, left, right);
_quick_sort(A, left, p - 1);
_quick_sort(A, p + 1, right);
}
}
void quick_sort(vector<int> &A) {
_quick_sort(A, 0, A.size() - 1);
}
值得改进的地方：
- 对于快排函数
static void _quick_sort(vector<int> &A, int left, int right)，当数组规模较小时，为了减小递归深度，我们可以改用简单排序（如冒泡排序或插入排序等）来进行小规模数据的排序。例如我们可以设定一个阈值cutOff=100，当待排数组长度high - low小于阈值cutOff时，就使用简单排序 - 主元的选定很关键，如果我们每次都能选定序列的中位数作为pivot，就能达到最好的时间复杂度。所以我们可以选择待排数组的头、中、尾这三个数的中位数进行近似
选主元的方法：
- 可以随机取（但随机函数耗费时间）
- 取头，中，尾的中位数
- 或者取五个数的中位数，或者取7个数的中位数
代码实现：
static int median3(vector<int> &A, int low, int high) {
int mid = (low + high) / 2;
if (A[low] > A[mid]) swap(A[low], A[mid]);
if (A[low] > A[high]) swap(A[low], A[high]);
if (A[mid] > A[high]) swap(A[mid], A[high]);
return mid;
}
子集划分：
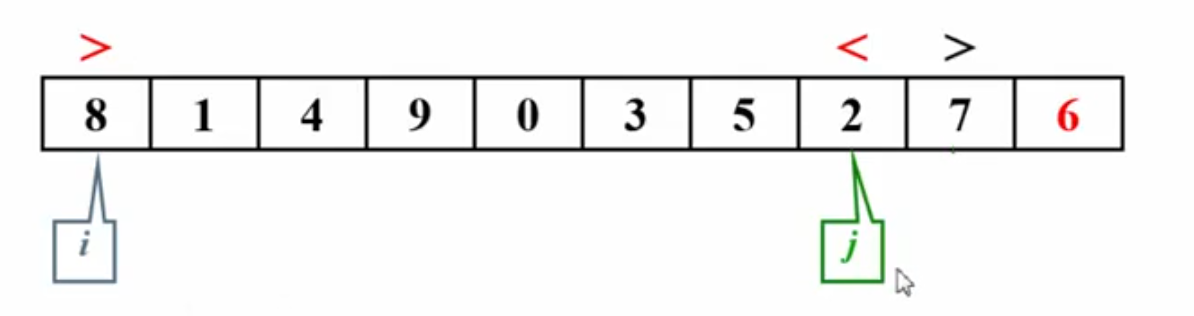
首尾两个指针，i指向8>6，不满足顺序，i停下；j指向7>6，满足顺序，前移指向2<6，不满足顺序，j停下
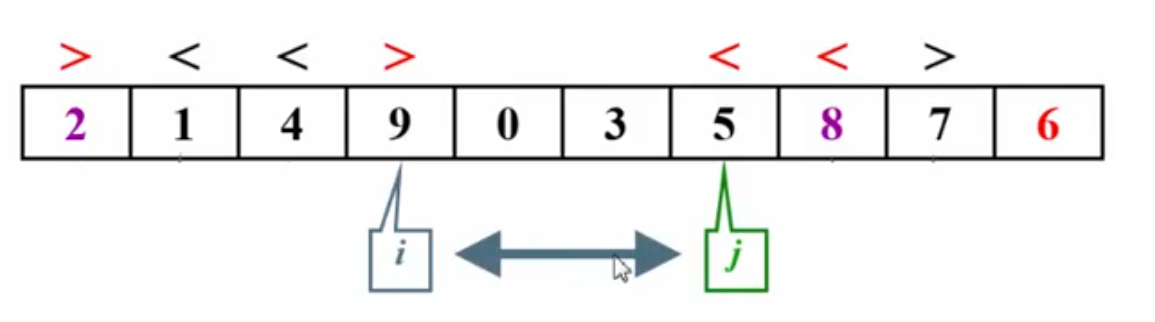
两者都停下后，交换指向的两个元素使之满足顺序，再移动i和j，重复上述步骤：
i超过j时停下，此时i所指向的位置就是6应该存放的位置：
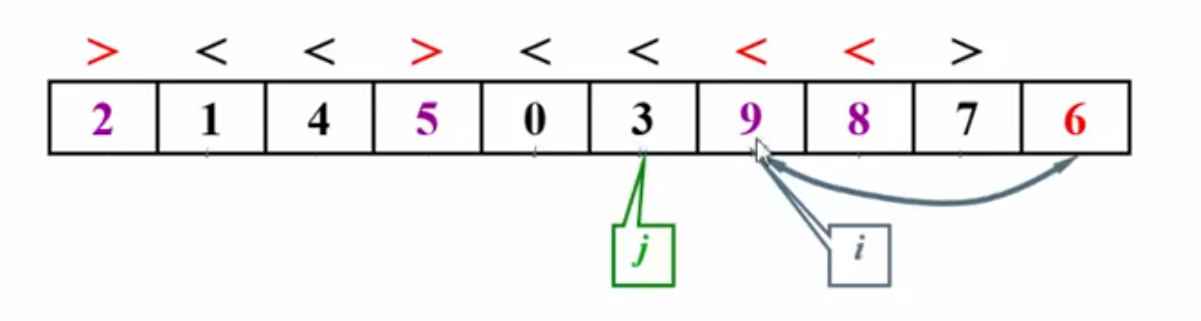
被选定的主元在子集划分完成之后就一次性的放在了正确的位置上，不像插入排序，还要移动位置
如果有元素正好等于pivot，也要停下来交换
小规模数据的处理：
如果数据充分小，使用插入排序：
表排序
当待排序的元素体积很大的时候，上面的排序算法已经不再适用，转而采用表排序
间接排序：只排序指向元素的指针
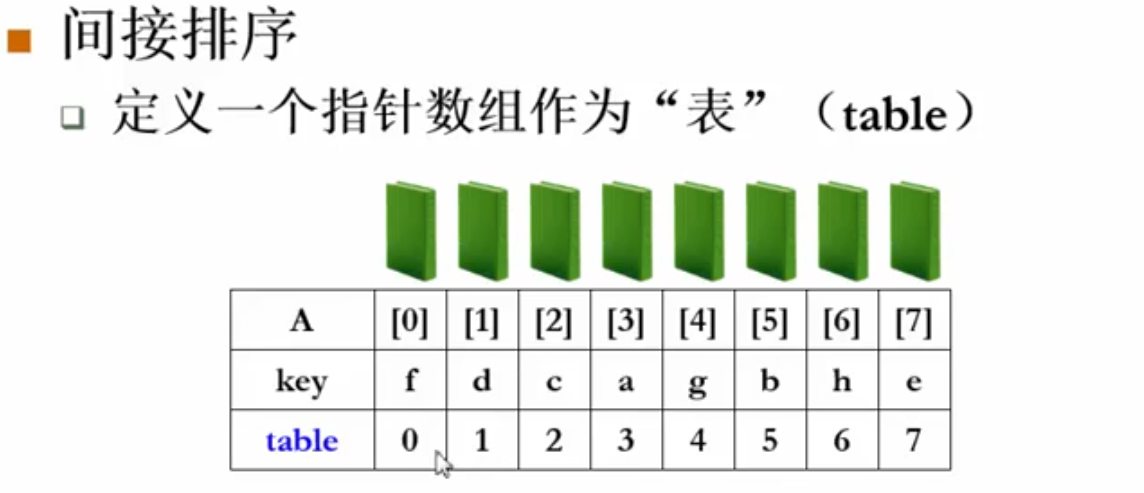
排序结果：
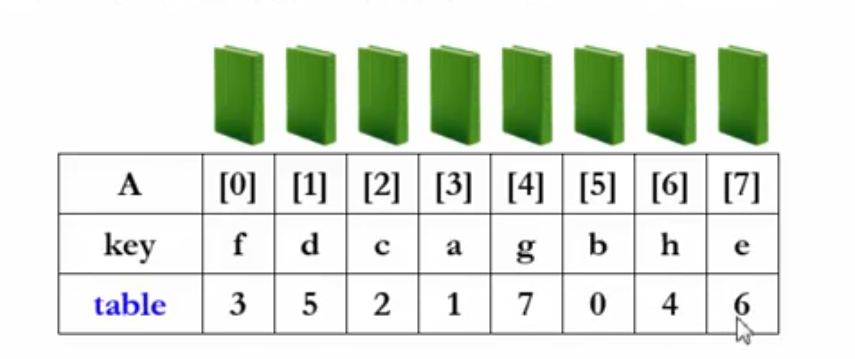
table中存储的是下标，第0个元素正确的下标存在table[0]，第1个元素正确的下标存在table[1]中，依次类推：
如果一定要对这些物体进行排序（物理排序），应用定理：N个数字的排列由若干个独立的环组成
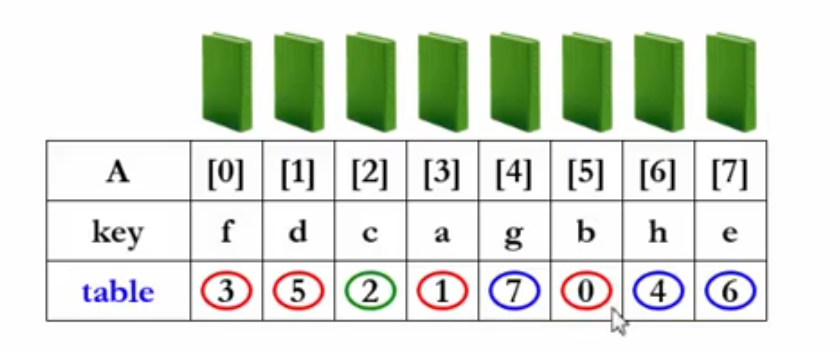
三个环：
- 0-3-1-5-0;
- 2-2;
- 4-7-6-4;
首先将环首元素取出，存放到一个临时变量，然后将环内元素依次前移，最后将取出的环首元素放到最后空出的位置
如何判断一个环的结束：if(table[i]=i)，每当移动好一个元素，就将其table的值改为i的值
时间复杂度：
桶排序（计数排序）
基于比较的排序的时间复杂度下界为n*logn，如果要破除，就要采用不是基于比较的算法
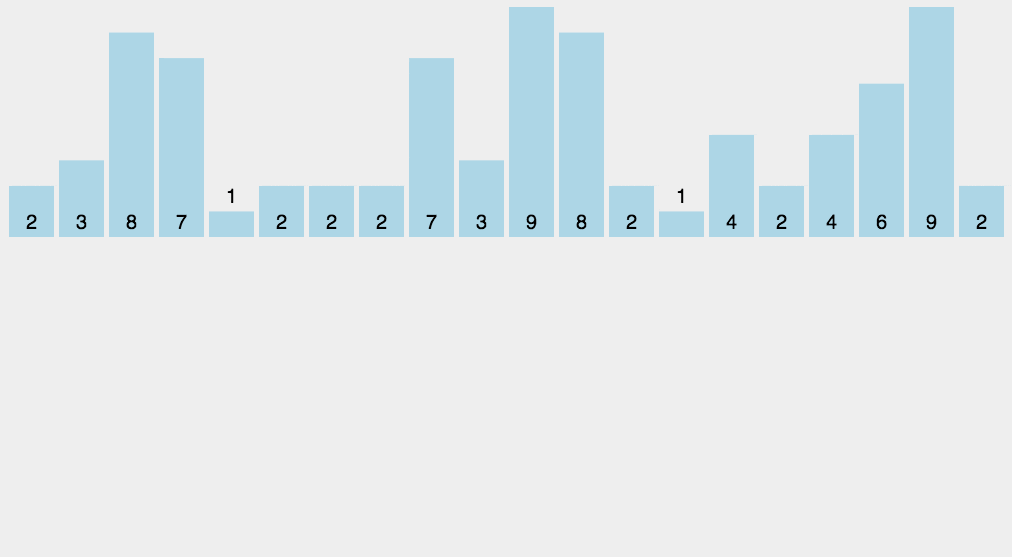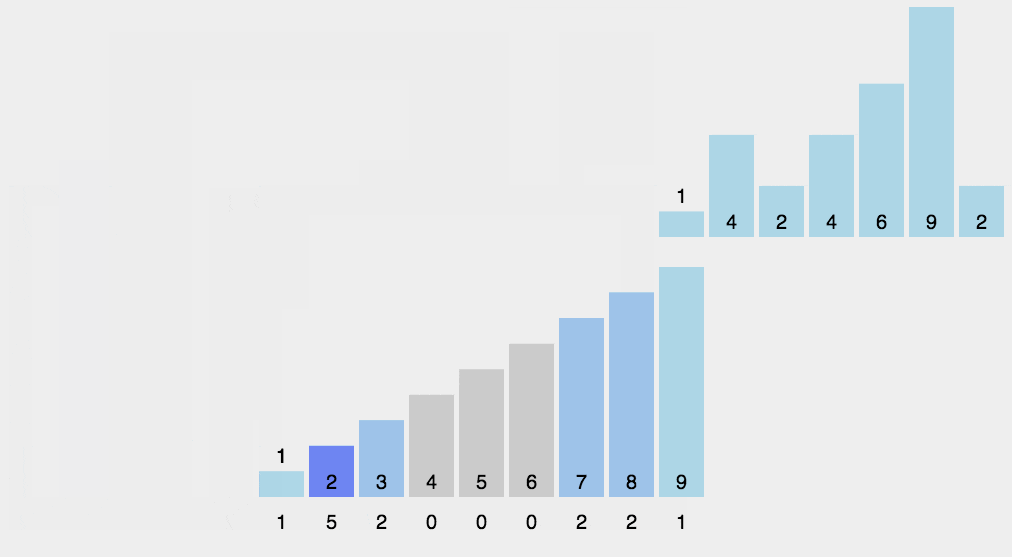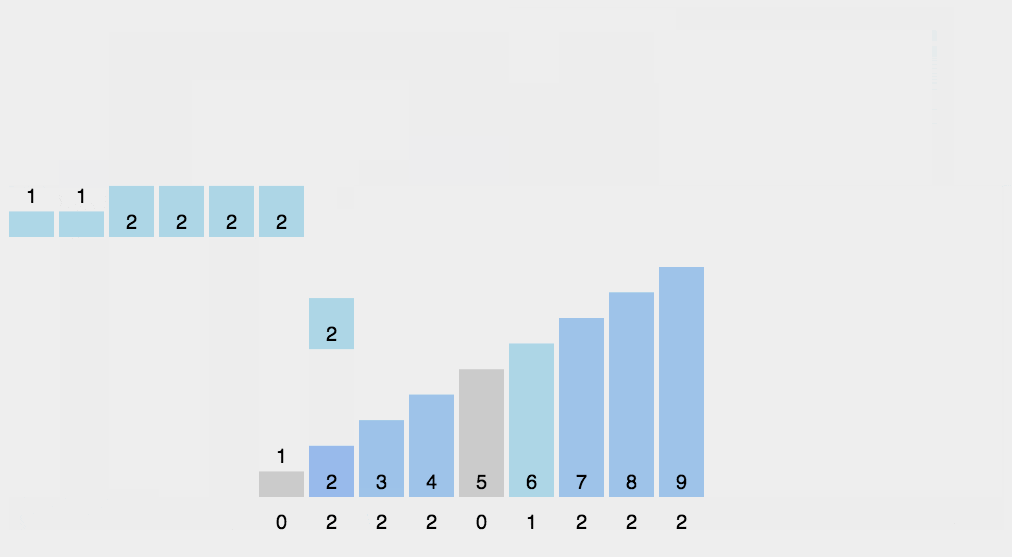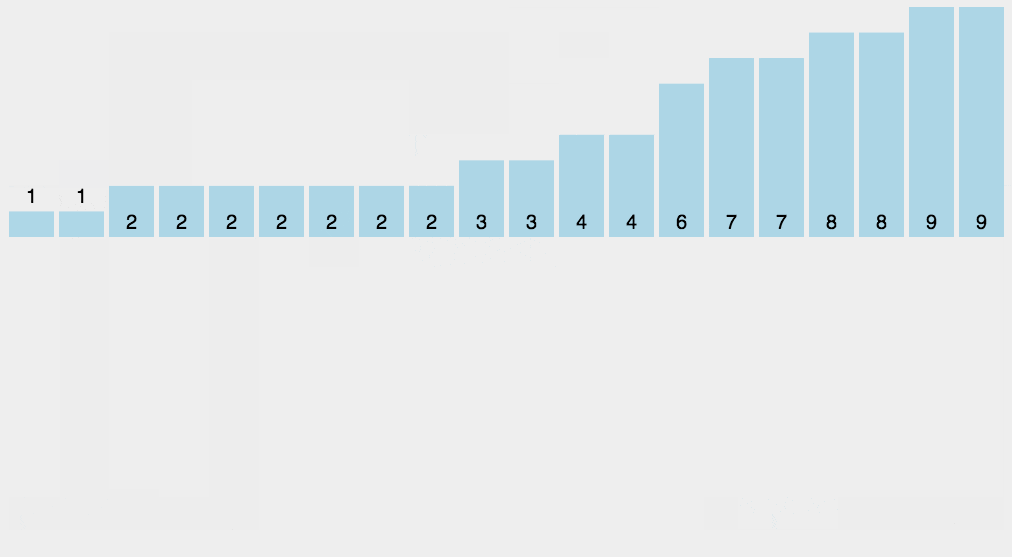
作为一种基于非比较类的排序，计数排序的的时间复杂度为O(n)，但这是以牺牲空间为代价的，其空间复杂度为O(n+max)，与数组中最大元素的值有关
- 首先遍历一遍数组找到其最大值存入
max中 - 接着开辟一个
max大小的辅助空间，也就是桶bucket - 接着遍历待排数组，将其每个元素
A[i]看做bucket的下标，执行bucket[A[i]]++。如果将数组看成一种map映射的话，其下标相当于key，数组元素值相当于value，遍历完成后，bucket中就存储了A中每个元素出现的次数 - 最后从
0到max遍历bucket，利用bucket中保存的数组元素的出现次数的信息形成已排序数组
初始化M个元素的桶，然后将每个学生的成绩插入到桶对应的链表中去：
当然，计数排序只能在数组中元素都大于0的情况下使用
代码实现：
void Counting_Sort(SortElemType A[], int N) {
printf("%s:", __func__);
SortElemType max = A[0];
for (int i = 1; i < N; ++i) {
if (A[i] > max)
max = A[i];
}
SortElemType* bucket = (SortElemType*)malloc(sizeof(SortElemType) * max);
memset(bucket, 0, max);
if (bucket != NULL) {
for (int i = 0; i < N; ++i) {
bucket[A[i]]++;
}
for (int i = 0, j = 0; i <= max; ++i) {
while ((bucket[i]--) > 0)
A[j++] = i;
}
free(bucket);
return;
} else {
printf("空间不足n");
return;
}
}
基数排序
- 遍历序列找出最大的数
max，并确定其位数digit_num - 开辟一个与数组
A大小相同的临时数组temp - 进入外层对每一数位进行处理的循环
for (i = 1; i <= digit_num; ++i, radix *= 10;) - 用一个
count数组统计原数组中某一位（从低位向高位统计）相同的数据出现的次数 - 对
count数组进行递推累加，这样，count中的每个count[i]都保存了从count[0]到count[i]的和 - 最后和计数排序一样，利用
count中保存的数组元素的出现次数的信息形成已排序数组temp - 将
tmep数组拷回到原数组中，进入下一轮每一数位进行处理的循环
代码实现
void Radix_Sort(SortElemType A[], int N) {
printf("%s:", __func__);
SortElemType max = A[0];
for (int i = 1; i < N; ++i) {
if (A[i] > max)
max = A[i];
}
int digit_num = 0;
while (max) {
max /= 10;
digit_num++;
}
SortElemType count[10];
SortElemType* temp = (SortElemType*)malloc(sizeof(SortElemType) * N);
int i, j, k;
int radix = 1;
for (i = 1; i <= digit_num; ++i, radix *= 10) {
memset(count, 0, 10 * sizeof(SortElemType));
for (j = 0; j < N; ++j) {
k = (A[j] / radix) % 10;
count[k]++;
}
for (j = 1; j < 10; ++j) {
count[j] = count[j - 1] + count[j];
}
for (j = N - 1; j >= 0; j--) {
k = (A[j] / radix) % 10;
temp[count[k] - 1] = A[j];
count[k]--;
}
//将temp中的元素倒回A
for (j = 0; j < N; ++j) {
A[j] = temp[j];
}
}
free(temp);
}
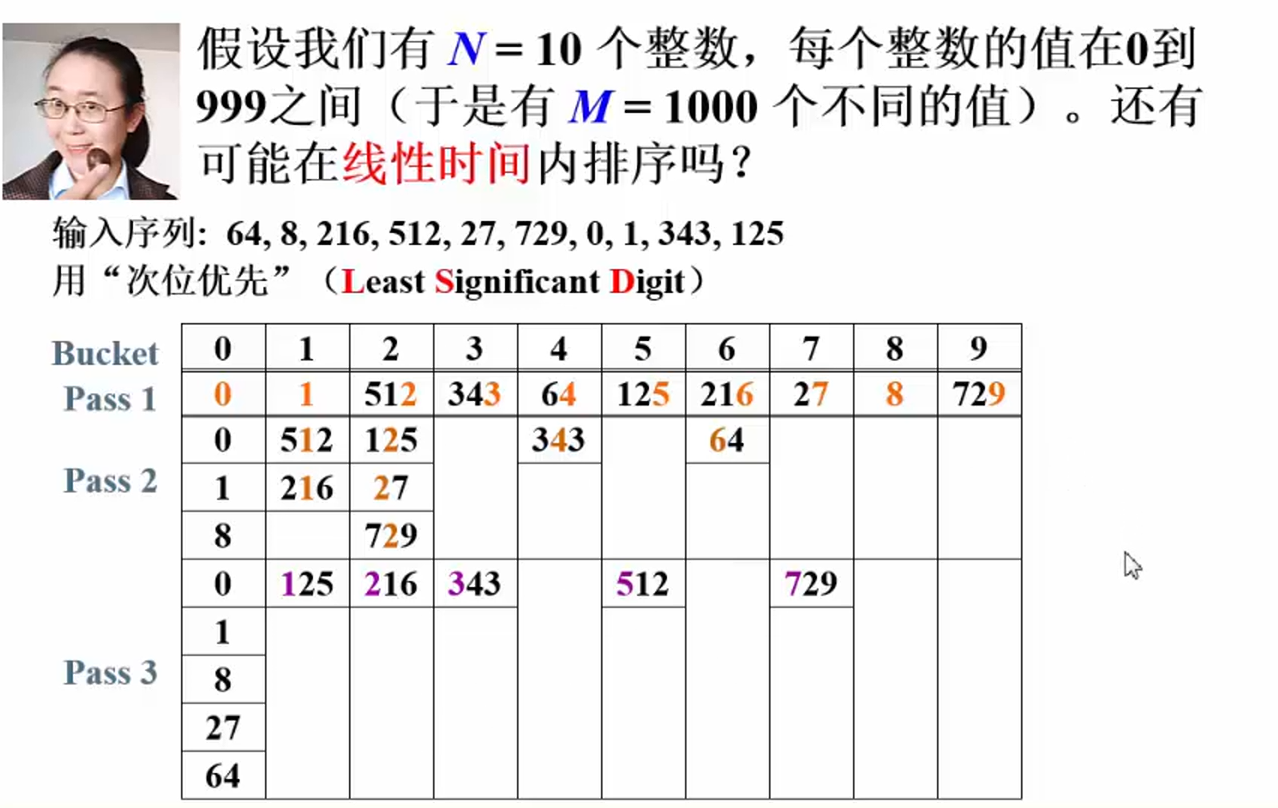
先排个位，再排十位，最后排百位
时间复杂度：O(P*(N+B))；
多关键字的排序
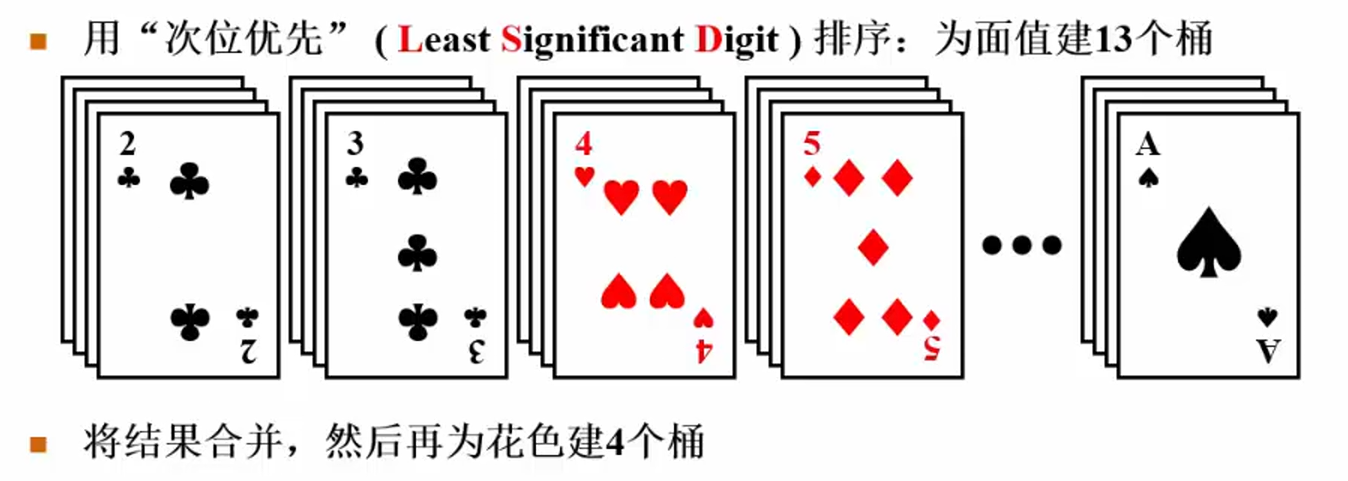
花色为主关键字，面值为次关键字
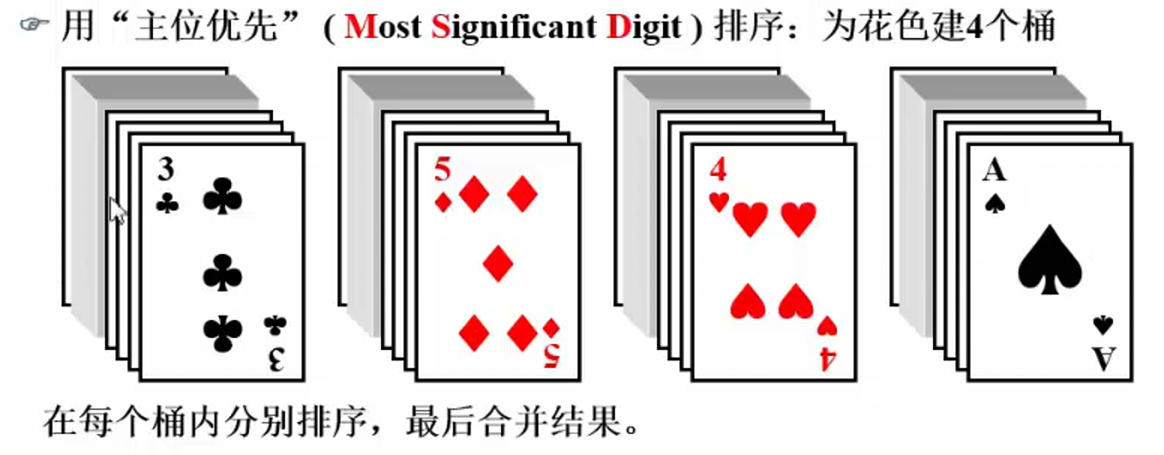
用次位优先效果更好，桶即为顺序，最后按花色合并即可：
排序算法的比较
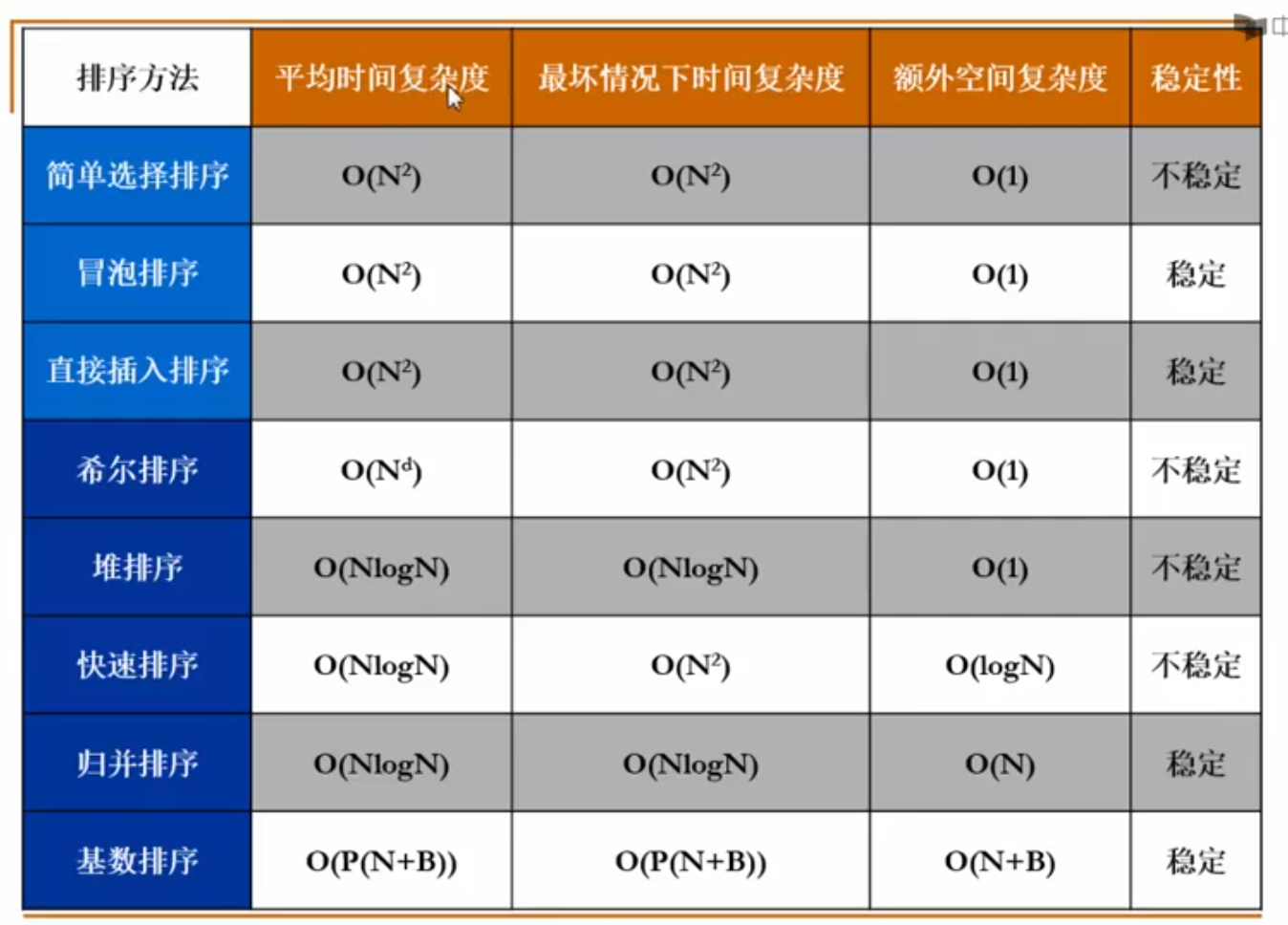
与堆排序相比，快速排序的n前常数比较小，更适合实际应用
InsertOrMerge
插入排序比较容易判断：
而归并排序的关键在于判断归并段的长度：
l=2时判断序列是否4有序，l=4时判断序列是否8有序……
最小的N=4
SortWithSwap(0,i)
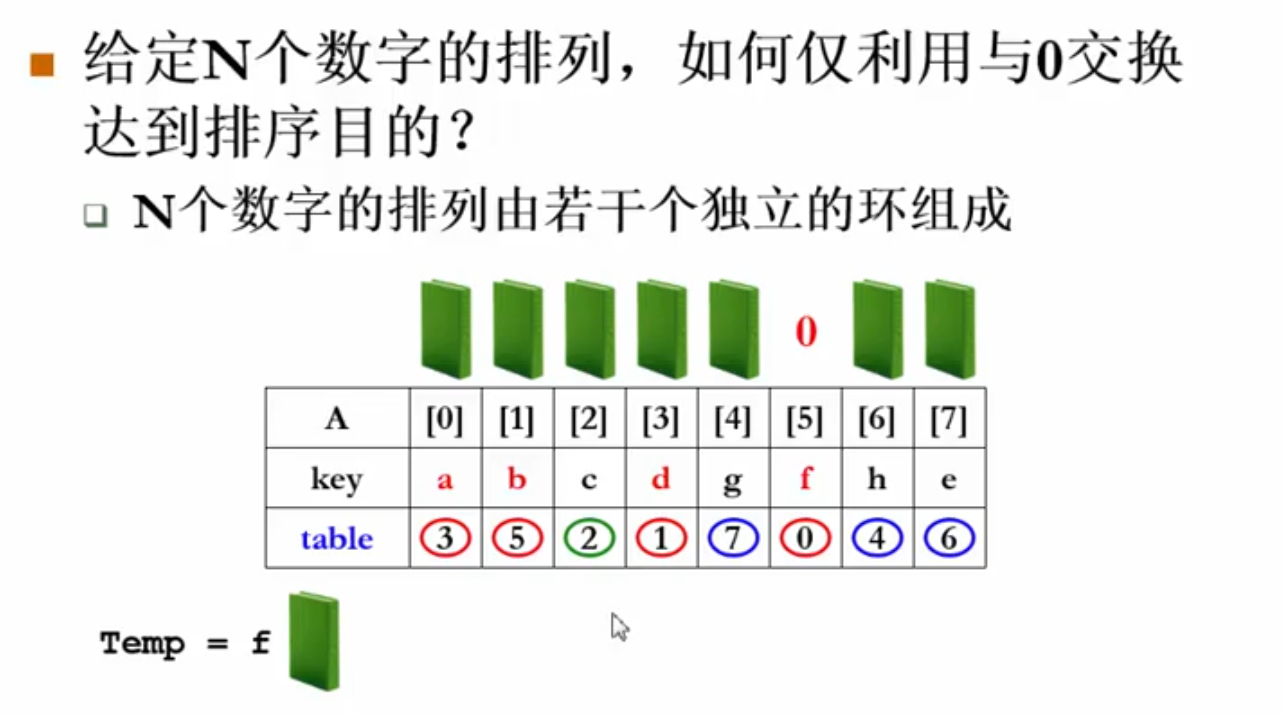环的分类：
六、散列
散列的基本思路
对于像字符串这种不方便直接比较的对象如何进行查找：
散列表
ADT描述：
一个实例：
分离链接法则装填引子定义成每个链表的平均长度
比较合适的α大小是0.5~0.8
一般对于一组整数的哈希函数采用取模运算实现比较简单：
H a s h ( k e y ) = k e y m o d T a b l e S i z e Hash(key)=key mod TableSize Hash(key)=key mod TableSize
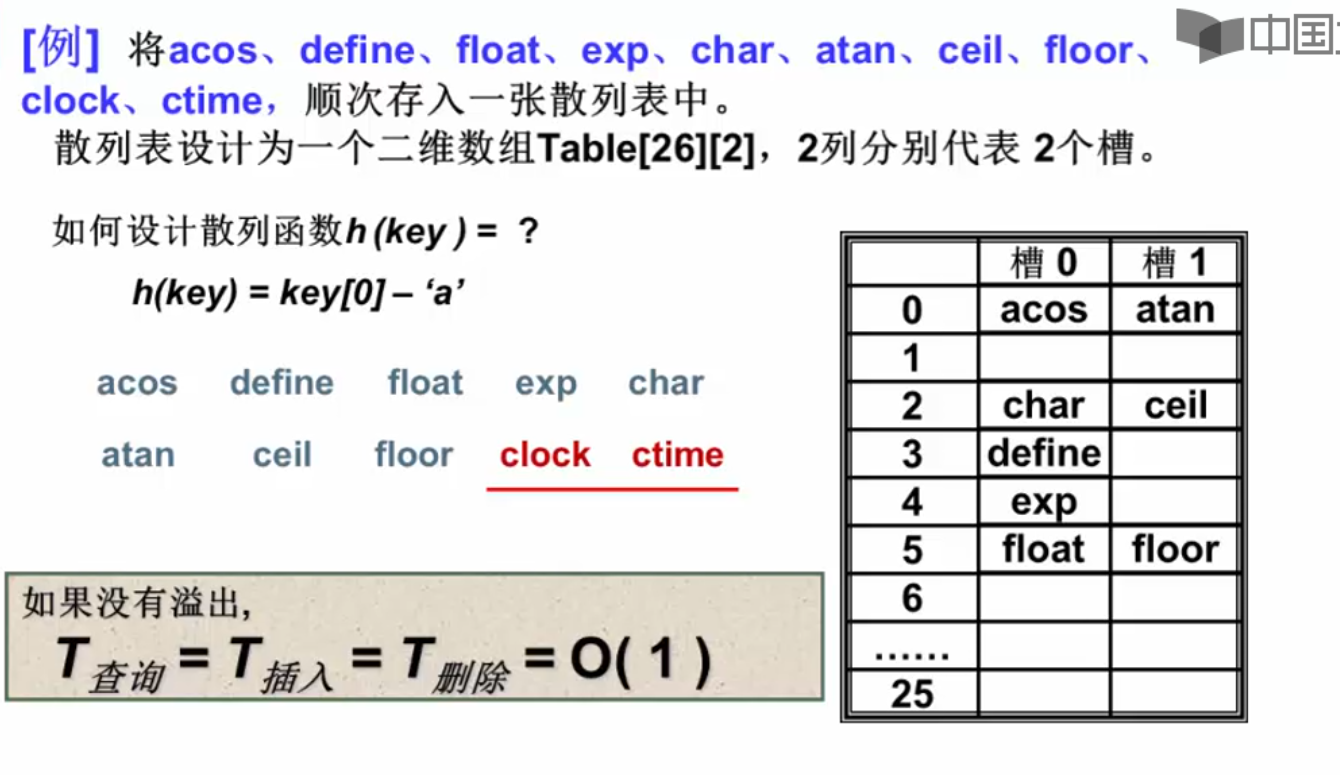对于一组字符串的最简单的哈希函数：
H a s h ( k e y ) = k e y [ 0 ] − ′ a ′ Hash(key)=key[0]- 'a' Hash(key)=key[0]− ′a′
如果没有冲突的话，散列查找只需要O(1)的时间复杂度
通常关键词的值域远大于表空间的地址集，所以说冲突不可能避免，只能减少
数字关键字的散列函数构造
一个好的hash函数应该满足：
- 计算简单，以便提高转换速度
- 关键词对应的地址空间分布均匀，以尽量减少冲突
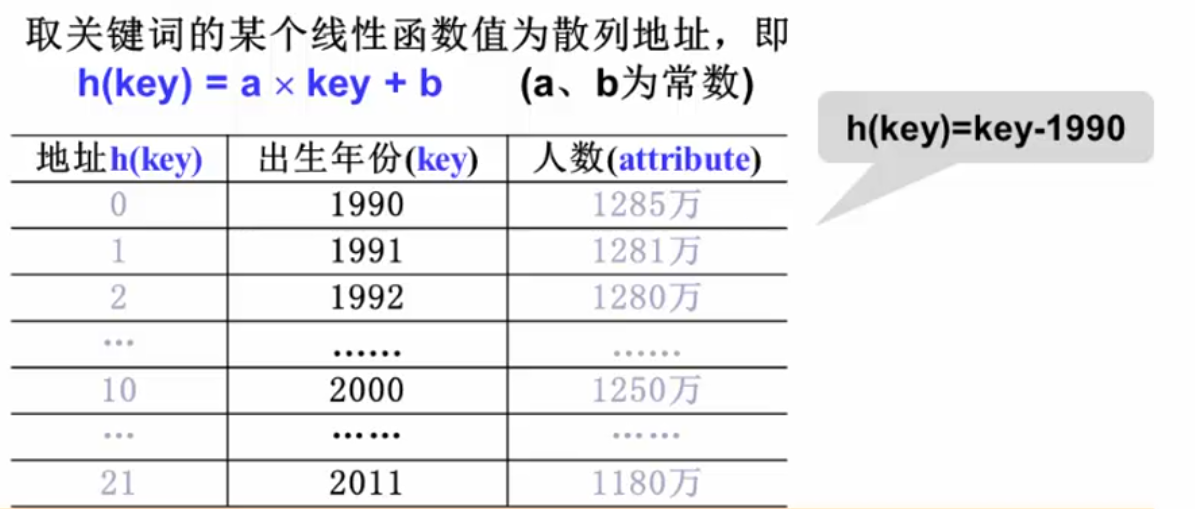
直接定址法：
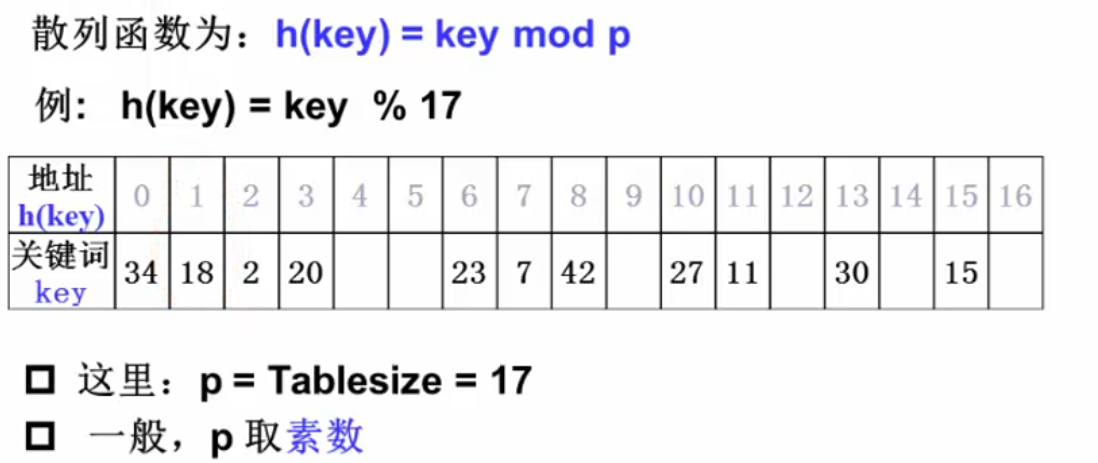
除留余数法：
数字分析法：分析数据对象的关键字在每一位上的表现，取随机性比较强的那些数位
折叠法：把关键字分割成位数相同的几个部分，然后叠加
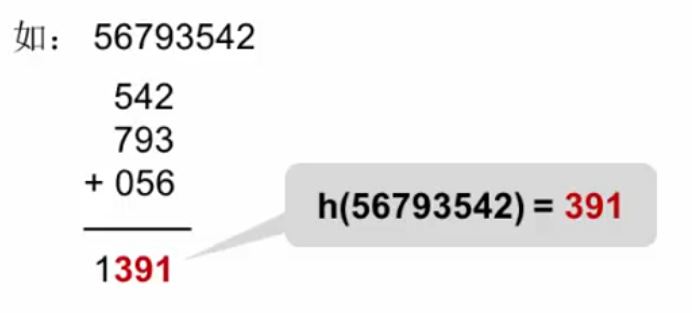
平方取中法：
折叠法和平方取中法都是为了让散列结果尽可能受到关键字每一位的影响
字符串关键字的散列函数构造
移位法散列函数：
h ( " a b c d " ) = a ∗ 3 2 4 + b ∗ 3 2 3 + c ∗ 3 2 2 + d ∗ 32 + e h("abcd") = a * 32^4 + b*32^3 + c * 32^2 + d * 32 + e h("abcd")=a∗324+b∗323+c∗322+d∗32+e
代码实现：
unsigned int hashStrToInt(const char* key, int tableSize) {
unsigned int h = 0;
while (*key != ' ') {
h = (h << 5) + *key++;
}
return h % tableSize;
}
处理冲突-开放定址法
常用处理冲突的思路：
- 换个位置：开放定址法
- 同一位置的冲突对象组织在一起：链地址法
Open Addressing：一旦产生了冲突（该地址已经有其他元素），就按某种规则去寻找另一空地址
开放地址法有三种不同的探测方法：
- 线性探测
- 平方探测
- 双散列
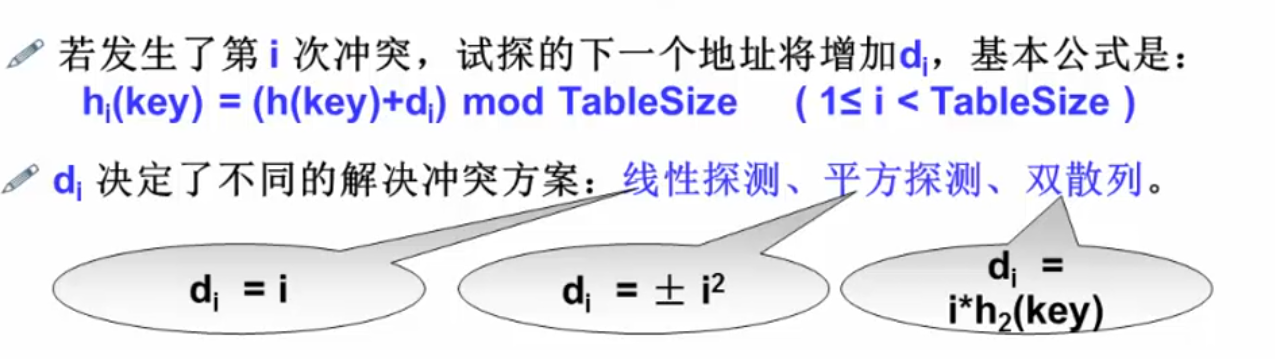
处理冲突-开放定址法-线性探测
增量序列：1,2,3…(TableSize-1)
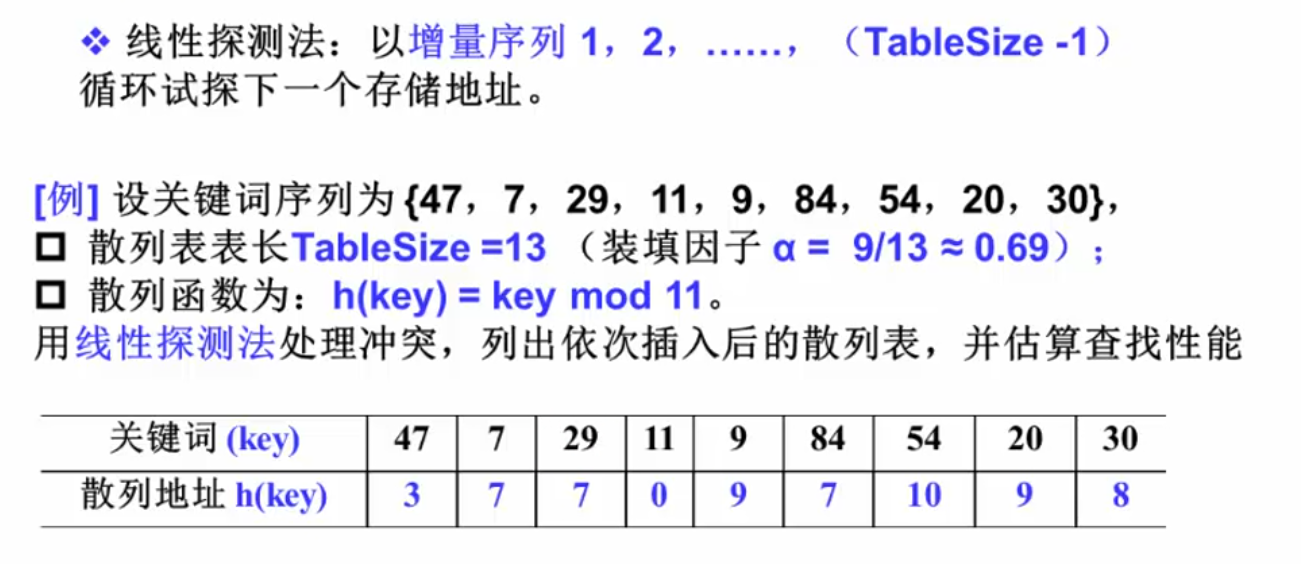
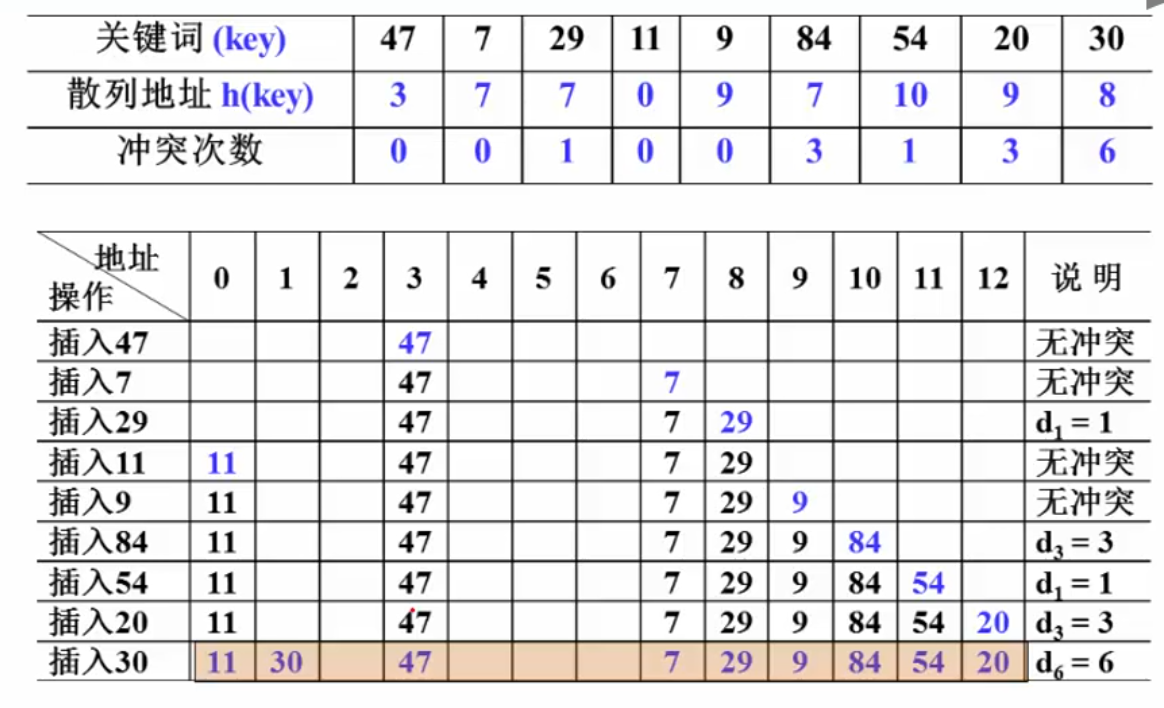最后可以看到产生了聚集现象：在某一个位置产生冲突后，在该位置附近产生冲突的次数会越来越
多，这也是线性探测存在的问题
性能分析：
- 成功平均查找长度ASLs
- 不成功平均查找长度ASLu
字符串的例子，散列结果：
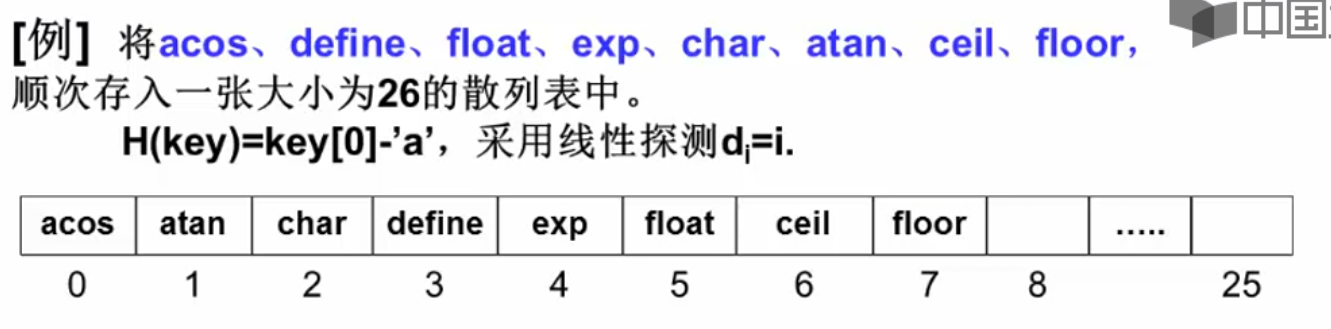性能分析：
处理冲突-开放定址法-平方探测法
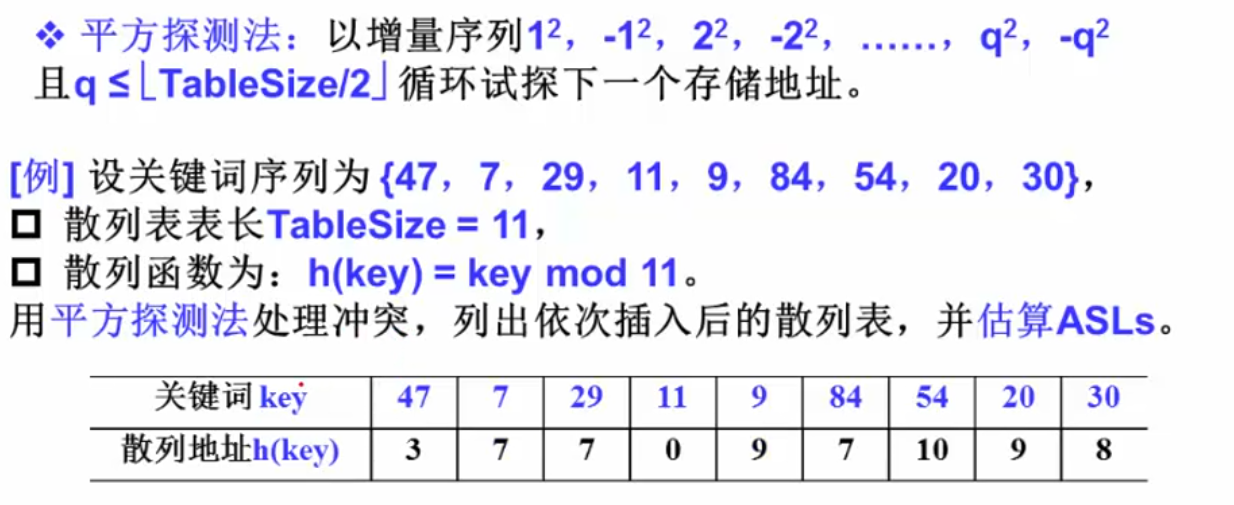散列结果：
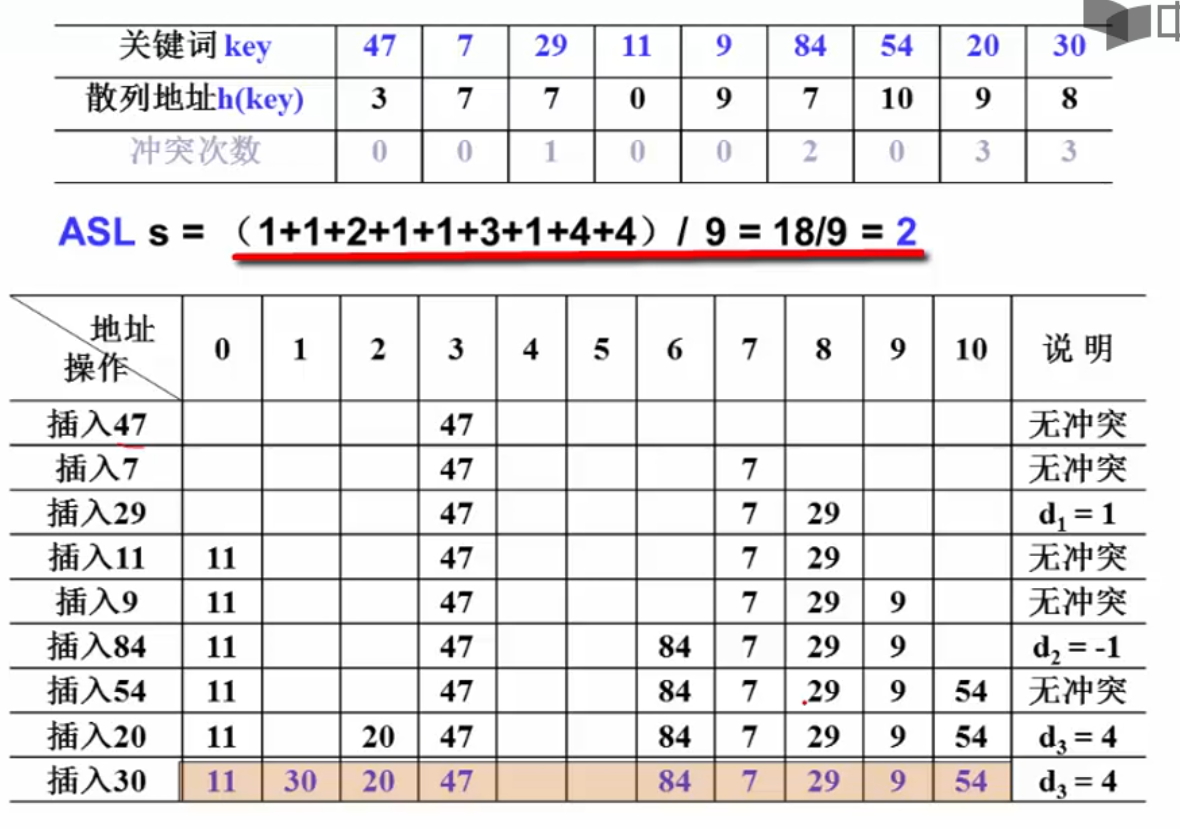在某些情况下，平方探测可能无法遍历整个散列表。
要探查整个散列表空间，要求TableSize=4k+3形式的素数。
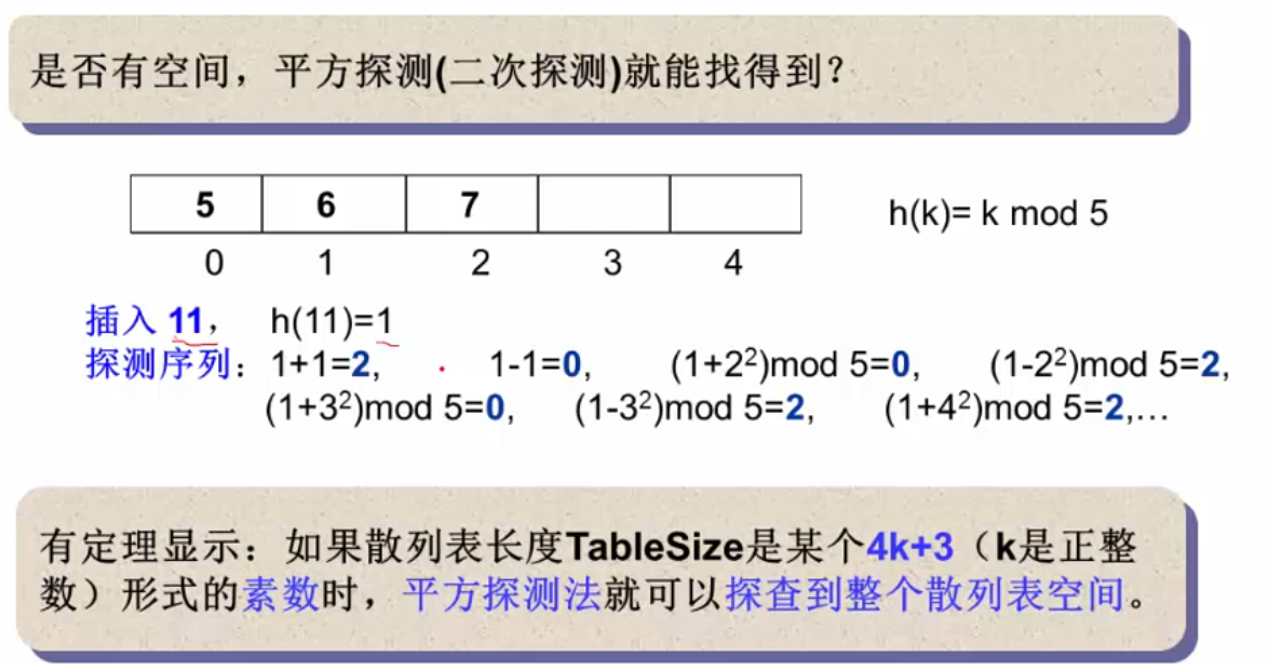平方探测很大程度上缓解了线性探测存在的聚集问题。
平方探测法代码实现：
类型定义：
#define MAXTABLESIE 65536
typedef int ElementType;
typedef int Index;
typedef int Position;
typedef enum {
Legitimate,
Empty,
Deleted
} EntryType;
typedef struct HastEntry {
ElementType Data;
EntryType Info;
} Cell;
struct HashTableNode {
int TableSize;
Cell* Cells;
};
typedef struct HashTableNode* HashTable;
对于整型数据，除留余数法的散列函数：
int Hash_divideKeepRemainder(ElementType key, int tableSize) {
return key % tableSize;
}
构造和销毁散列表：
//寻找大于n且不超过MAXTABLESIZE的最小素数
int NextPrim(int n) {
int p = (n & 1) ? (n + 2) : (n + 1);
int i = 0;
while (p <= MAXTABLESIE) {
for (i = (int)sqrt(p); i > 2; --i) {
if (p % i == 0)
break;
}
if (i == 2)
break;
else
p += 2;
}
return p;
}
HashTable CreateHashTable(int TableSize) {
HashTable h = (HashTable)malloc(sizeof(struct HashTableNode));
if (h == NULL)
return NULL;
h->TableSize = NextPrim(TableSize);
h->Cells = (Cell*)malloc(sizeof(Cell) * h->TableSize);
if (h->Cells == NULL) {
free(h);
return NULL;
}
for (int i = 0; i < h->TableSize; ++i) {
h->Cells[i].Info = Empty;
}
return h;
}
void DestoryHashTable(HashTable h) {
if (h == NULL)
return;
if (h->Cells != NULL)
free(h->Cells);
free(h);
return;
}
平方探测法查找的实现和插入元素的实现：
Position Find_quadraticProbing(HashTable h, ElementType key) {
int collisionCount = 0;
Position newPosition = Hash_divideKeepRemainder(key, h->TableSize);
Position currentPosition = newPosition;
while ((h->Cells[newPosition].Info != Empty) && (h->Cells[newPosition].Data != key)) {
if ((++collisionCount) & 2) {
newPosition = currentPosition + (collisionCount + 1) * (collisionCount + 1) / 4;
if (newPosition >= h->TableSize)
newPosition = newPosition % (h->TableSize);
} else {
newPosition = currentPosition - collisionCount * collisionCount / 4;
while (newPosition < 0)
newPosition += h->TableSize;
}
}
return newPosition;
}
bool InsertHashTable(HashTable h, ElementType key) {
Position p = Find_quadraticProbing(h, key);
if (h->Cells[p].Info == Empty || h->Cells[p].Info == Deleted) {
h->Cells[p].Info = Legitimate;
h->Cells[p].Data = key;
return true;
} else {
return false;
}
}
哈希表中采用懒惰删除，这样我们在探测是就会知道该位置是真的空了终止探测还是应该继续探测下去
双散列法：
再散列：α过大时会严重降低查找效率，解决方法是加倍扩大散列表，这样α/=2，并将原表中的数据重新计算分配到新表中去
分离链接法
将所有关键字为同义词的数据对象通过结点链接存储到同一个单链表中
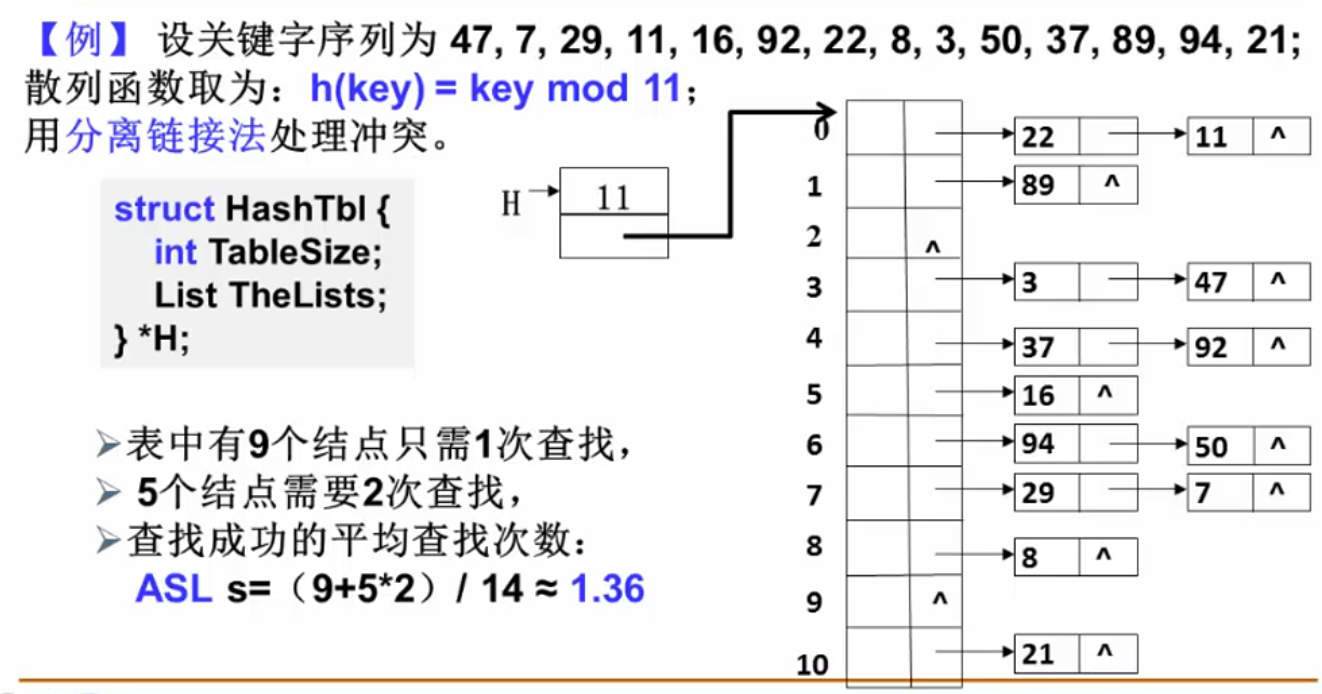分离链接法相关操作代码实现：
#define KEYLENGTH 15
#define MAXTABLESIZE 65536
typedef char ElementType[KEYLENGTH + 1];
typedef int Index;
typedef struct LNode* PtrToLNode;
struct LNode {
ElementType Data;
PtrToLNode Next;
};
typedef PtrToLNode Position;
typedef PtrToLNode List;
typedef struct HashTableNode* HashTable;
struct HashTableNode {
int TableSize;
List Heads;
};
int NextPrime(int n) {
int p = (n & 2) ? (n + 2) : (n + 1);
int i = 0;
while (p <= MAXTABLESIZE) {
for (i = p / 2; i > 2; --i) {
if (p % i == 0)
break;
}
if (i == 2)
break;
else
p += 2;
}
return p;
}
//"adcb"
int Hash_strToInt(const char* str, int tableSize) {
unsigned int h = 0;
while ((*str) != ' ') {
h = (h << 5) + *str++;
}
return h % tableSize;
}
HashTable CreateHashTable(int tableSize) {
HashTable h = (HashTable)malloc(sizeof(struct HashTableNode));
h->TableSize = NextPrime(tableSize);
h->Heads = (List)malloc(sizeof(struct LNode) * (h->TableSize));
for (int i = 0; i < h->TableSize; ++i) {
h->Heads[i].Data[0] = ' ';
h->Heads[i].Next = NULL;
}
return h;
}
void DestoryHashTable(HashTable h) {
Position p, t;
for (int i = 0; i < h->TableSize; ++i) {
p = h->Heads[i].Next;
while (p) {
t = p->Next;
free(p);
p = t;
}
}
free(h->Heads);
free(h);
return;
}
Position Find(HashTable h, ElementType key) {
Index v = Hash_strToInt(key, h->TableSize);
Position p = h->Heads[v].Next;
while (p != NULL && strcmp(p->Data, key)) {
p = p->Next;
}
return p;
}
bool InsertHashTable(HashTable h, ElementType key) {
Position p = Find(h, key);
if (p == NULL) {
List newNode = (List)malloc(sizeof(struct LNode));
strcpy(newNode->Data, key);
Index v = Hash_strToInt(key, h->TableSize);
newNode->Next = h->Heads[v].Next;
h->Heads[v].Next = newNode;
return true;
} else {
return false;
}
}
散列表的性能分析
线性探测的查找性能：
平方探测和双散列探测的查找性能：
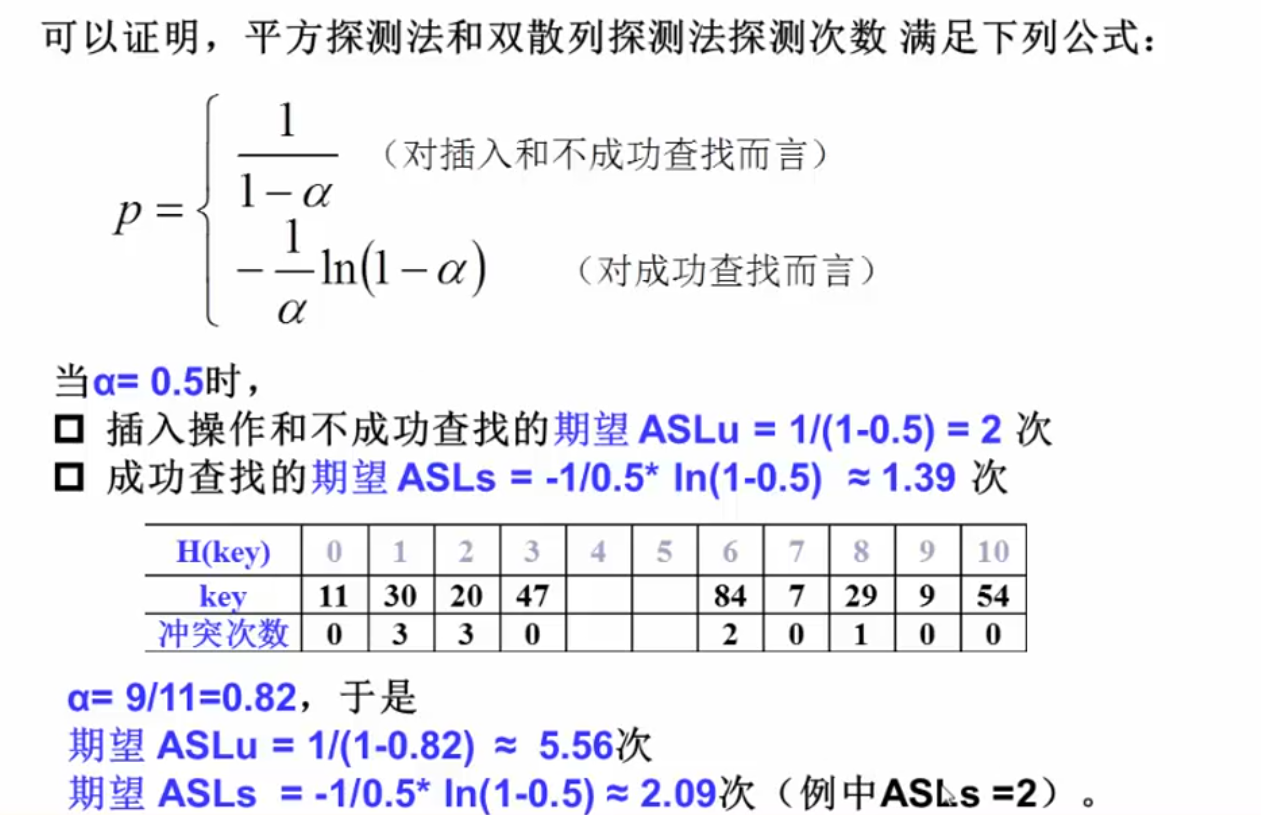分离链接法的查找性能：
α被定义为链表的平均长度，可以>1
散列的优缺点分析：
开放地址法优缺点：
分离链接法优缺点：
文件中单词词频统计
需求分析：
程序框架：
电话聊天狂人
题意理解：
解法一：排序
解法二：直接映射
解法三：散列
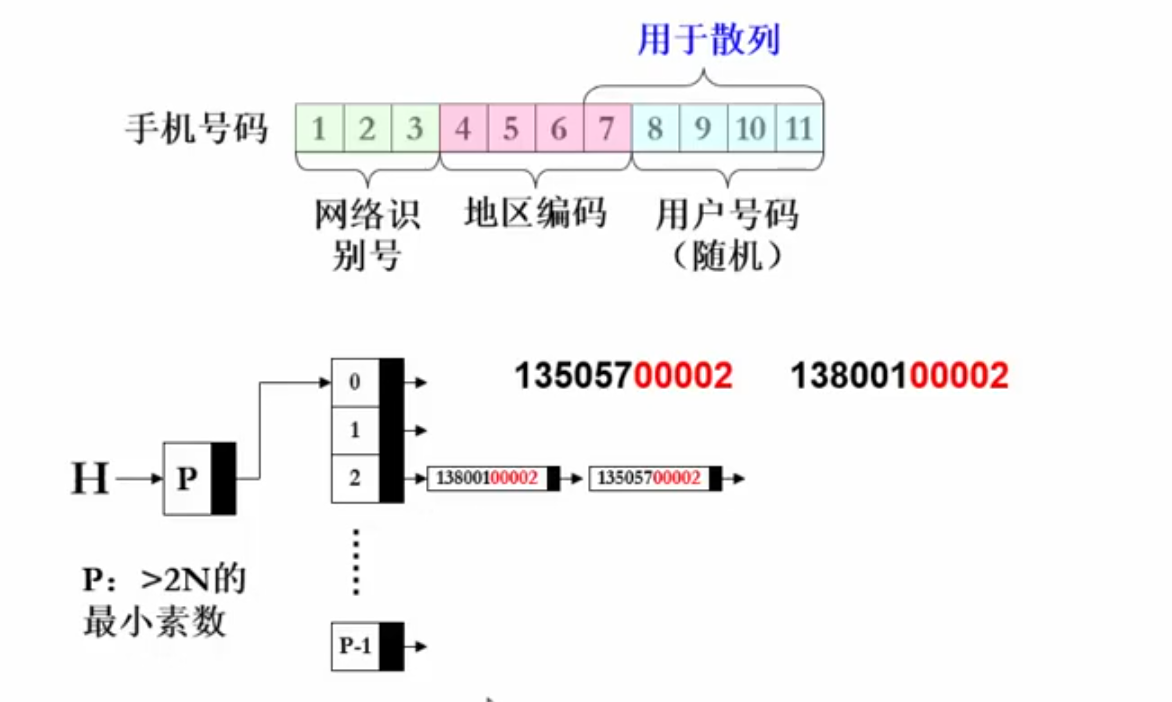
程序框架：
输出狂人：
模块的引用与裁剪：
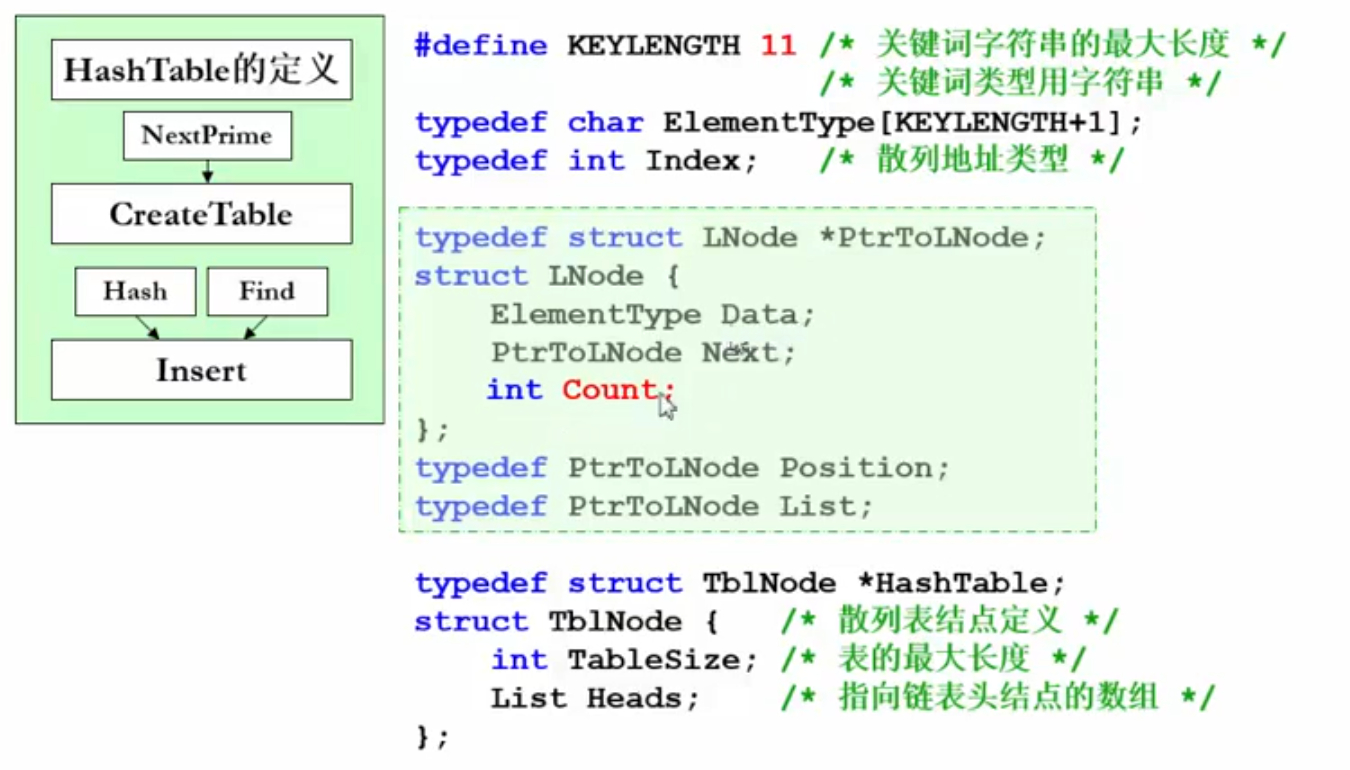
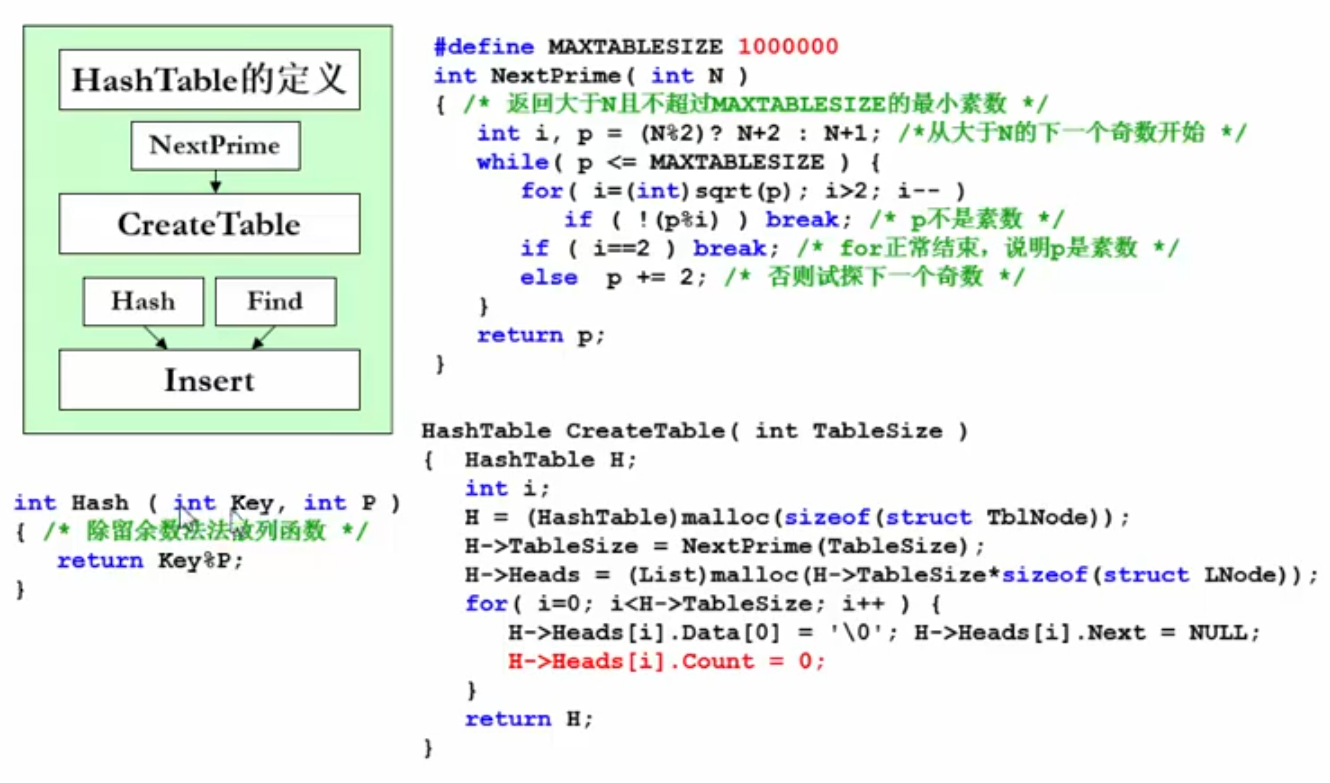
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define KEYLENGTH 11
#define MAXTABLESIZE 100000
#define ENGAGE_NUM 5
typedef char ElementType[KEYLENGTH + 1];
typedef int Index;
typedef struct LNode* PtrToLNode;
struct LNode {
ElementType Data;
PtrToLNode Next;
int Count;
};
typedef PtrToLNode Position;
typedef PtrToLNode List;
typedef struct HashTableNode* HashTable;
struct HashTableNode {
int TableSize;
List Heads;
};
int NextPrime(int n) {
int p = (n & 2) ? (n + 2) : (n + 1);
int i = 0;
while (p <= MAXTABLESIZE) {
for (i = p / 2; i > 2; --i) {
if (p % i == 0)
break;
}
if (i == 2)
break;
else
p += 2;
}
return p;
}
//"13303345089"
int Hash(const char* teleNum, int tableSize) {
//取倒数ENGAGE_NUM=5位手机号做哈希映射
unsigned int h = atoi(teleNum + KEYLENGTH - ENGAGE_NUM);
return h % tableSize;
}
HashTable CreateHashTable(int tableSize) {
HashTable h = (HashTable)malloc(sizeof(struct HashTableNode));
h->TableSize = NextPrime(tableSize);
h->Heads = (List)malloc(sizeof(struct LNode) * (h->TableSize));
for (int i = 0; i < h->TableSize; ++i) {
h->Heads[i].Data[0] = ' ';
h->Heads[i].Next = NULL;
h->Heads[i].Count = 0;
}
return h;
}
void DestoryHashTable(HashTable h) {
Position p, t;
for (int i = 0; i < h->TableSize; ++i) {
p = h->Heads[i].Next;
while (p) {
t = p->Next;
free(p);
p = t;
}
}
free(h->Heads);
free(h);
return;
}
Position Find(HashTable h, ElementType key) {
Index v = Hash(key, h->TableSize);
Position p = h->Heads[v].Next;
while (p != NULL && strcmp(p->Data, key)) {
p = p->Next;
}
return p;
}
bool InsertHashTable(HashTable h, ElementType key) {
Position p = Find(h, key);
if (p == NULL) {
List newNode = (List)malloc(sizeof(struct LNode));
strcpy(newNode->Data, key);
newNode->Count = 1;
Index v = Hash(key, h->TableSize);
newNode->Next = h->Heads[v].Next;
h->Heads[v].Next = newNode;
return true;
} else {
p->Count++;
return false;
}
}
void ScanAndOutput(HashTable h) {
ElementType minPhone;
minPhone[0] = ' ';
int maxCnt = 0;
//狂人计数
int personCnt = 0;
for (int i = 0; i < h->TableSize; ++i) {
for (PtrToLNode p = h->Heads[i].Next; p != NULL; p = p->Next) {
if (p->Count > maxCnt) {
strcpy(minPhone, p->Data);
maxCnt = p->Count;
personCnt = 1;
} else if (p->Count == maxCnt) {
personCnt++;
if (strcmp(p->Data, minPhone) < 0) {
strcpy(minPhone, p->Data);
}
}
}
}
printf("%s %d", minPhone, maxCnt);
if (personCnt > 1)
printf(" %d", personCnt);
printf("n");
}
int main(int argc, char* argv[]) {
int n;
ElementType key;
scanf("%d", &n);
HashTable h = CreateHashTable(2 * n);
for (int i = 0; i < n; ++i) {
scanf("%s", key);
InsertHashTable(h, key);
scanf("%s", key);
InsertHashTable(h, key);
}
ScanAndOutput(h);
DestoryHashTable(h);
return 0;
}
Hashing-HardVersion
示例：
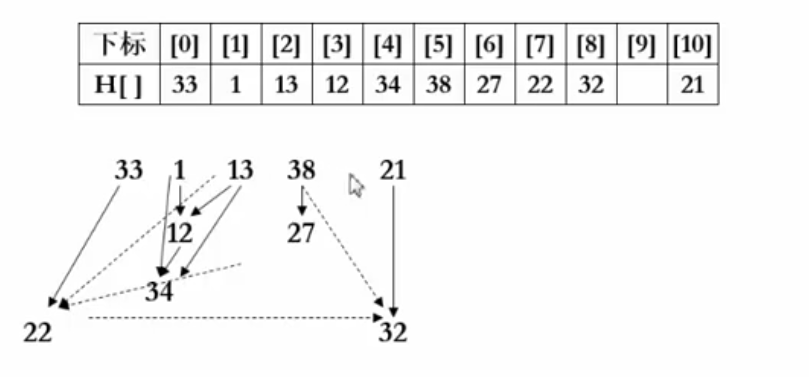
示例结果：
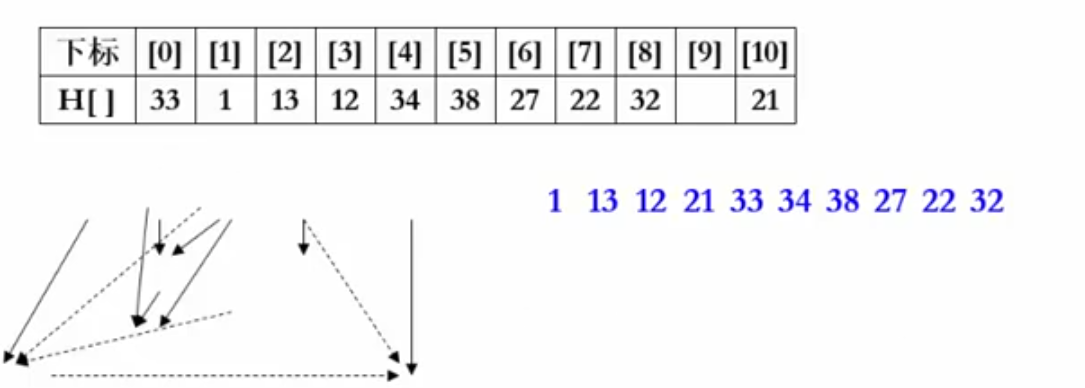
被处理的元素之间有非常明显的先后关系，问题的本质就是拓扑排序
七、KMP算法
KMP算法
什么是串：
模式匹配的目标：
方法一：使用C库函数strstr：
char *strstr(const char *haystack, const char *needle)
代码示例：
#include <stdio.h>
#include <string.h>
typedef char* Position;
char string[] = "This is a simple example";
char pattern[] = "simple";
void strstr_test();
void KMP_test();
int main(int argc, char* argv[]) {
strstr_test();
}
void strstr_test() {
Position p = strstr(string, pattern);
if (p) {
printf("%sn", p);
} else {
printf("Not foundn");
}
}
方法2，使用KMP算法（由Knuth, Morris, Pratt三个人发明）：
T
=
O
(
n
+
m
)
T=O(n+m)
T=O(n+m)
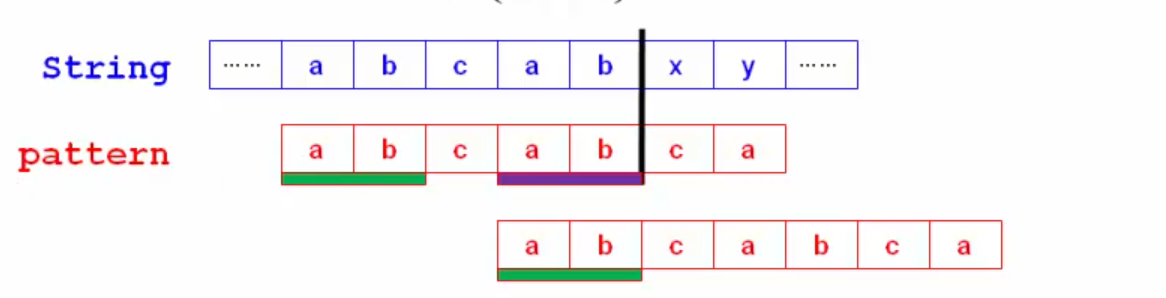
在已经匹配的部分中，找到最长的公共子串，下次移位时直接将前面的子串和后面的子串对齐即可，不必每次移动一位。这样string中的指针不会回溯
定义match函数构造next表：
m a t c h ( j ) = { 满足 p 0 . . . p i = p j − i . . . p j 的最大 i ( < j ) − 1 ，如果这样的 i 不存在 match(j)= begin{cases} 满足p_0...p_i=p_{j-i}...p_j的最大i(<j)\ -1，如果这样的i不存在 end{cases} match(j)={满足p0...pi=pj−i...pj的最大i(<j)−1，如果这样的i不存在
next(match)表：
match(j)只与比较小的 pattern子串有关，保存了子串中一首一尾能够匹配的最长子串的信息
if (str[s] == pattern[p])，说明当前字符匹配，s和p同时向后移动；
else if (p > 0)，当前字符失配，且不是模式串的第0个字符，就是下图的情况，需要将p指针回溯到绿色部分末尾，也就是p-1的match值：p = march[p - 1] + 1;
否则说明第一个字符就不匹配，++s；
代码实现：
int KMP(char const* str, char const* pattern) {
//获取str的长度O(n)
int n = strlen(str);
//获取pattern的长度O(m)
int m = strlen(pattern);
int s = 0, p = 0;
if (m > n)
return -1;
int* match = (int*)malloc(sizeof(int) * m);
//构造next表
buildMatch(pattern, match);
//都没有触达结尾O(n)，s从来没有回退过
while (s < n && p < m) {
if (str[s] == pattern[p]) {
//当前字符匹配
++s;
++p;
} else if (p > 0) {
//当前字符失配，跳转到上一个小子串末尾
p = match[p - 1] + 1;
} else {
//第一个字符就失配
++s;
}
}
free(match);
return (p == m) ? s - m : -1;
}
buildMatch函数的实现
递归地，当计算match[j]时，如果pattern[match[j-1] + 1] == pattern[j]，则可以直接得到match[j]=match[j-1]+1
如果没那么幸运pattern[match[j-1] + 1] != pattern[j]，也不至于回到起点重开，可以根据match[j-1]的match值，向前找到匹配的部分（下面第一块绿色部分），则对于相同的后半段，最后的紫色部分和最开始的绿色部分一定是匹配的，再利用上面的步骤即可
第一个问号是match[match[j-1]+1]，第二个问号当然是j
代码实现：
//kmp.h
void buildMatch(char const* pattern, int* match) {
int prev = 0, j = 0;
int m = strlen(pattern);
match[0] = -1;
for (j = 1; j < m; ++j) {
prev = match[j - 1];
while ((prev >= 0) && (pattern[prev + 1] != match[j])) {
// i不断回退
prev = match[prev];
}
if (pattern[j] == pattern[prev + 1]) {
// pattern[j]==pattern[match[j-1]+1]
match[j] = prev + 1;
} else {
//没有真子串可以匹配
match[j] = -1;
}
}
return;
}
Time Complexity：
i回退的总次数不会超过i增加的总次数。
T = O ( m ) T=O(m) T=O(m)
所以KMP算法的总的时间复杂度为： O ( n + m ) O(n+m) O(n+m)
最后
以上就是多情小甜瓜为你收集整理的浙大版数据结构学习笔记一、引言二、线性结构三、树四、图五、排序六、散列七、KMP算法的全部内容，希望文章能够帮你解决浙大版数据结构学习笔记一、引言二、线性结构三、树四、图五、排序六、散列七、KMP算法所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复