傅里叶谱方法求解基本偏微分方程—二维波动方程

二维波动方程

将一维波动方程中的一维无界弦自由振动方程推广到二维空间上, 就得到了描述无界 $(-\infty <x,y<\infty )$ 弹性薄膜的波动方程:
$$\frac{{\partial }^{2}u}{\partial t^2}=a^2\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right)u\text{\hspace{1em}(1)}$$
取 $a=1$, 初始条件为:
$${u|}_{t=0}={\mathrm{e}}^{-20\left[(x-0.4{)}^2+(y+0.4{)}^2\right]}+{\mathrm{e}}^{-20\left[(x+0.4{)}^2+(y-0.4{)}^2\right]},{\frac{\partial u}{\partial t}|}_{t=0}=0\text{\hspace{1em}(2)}$$
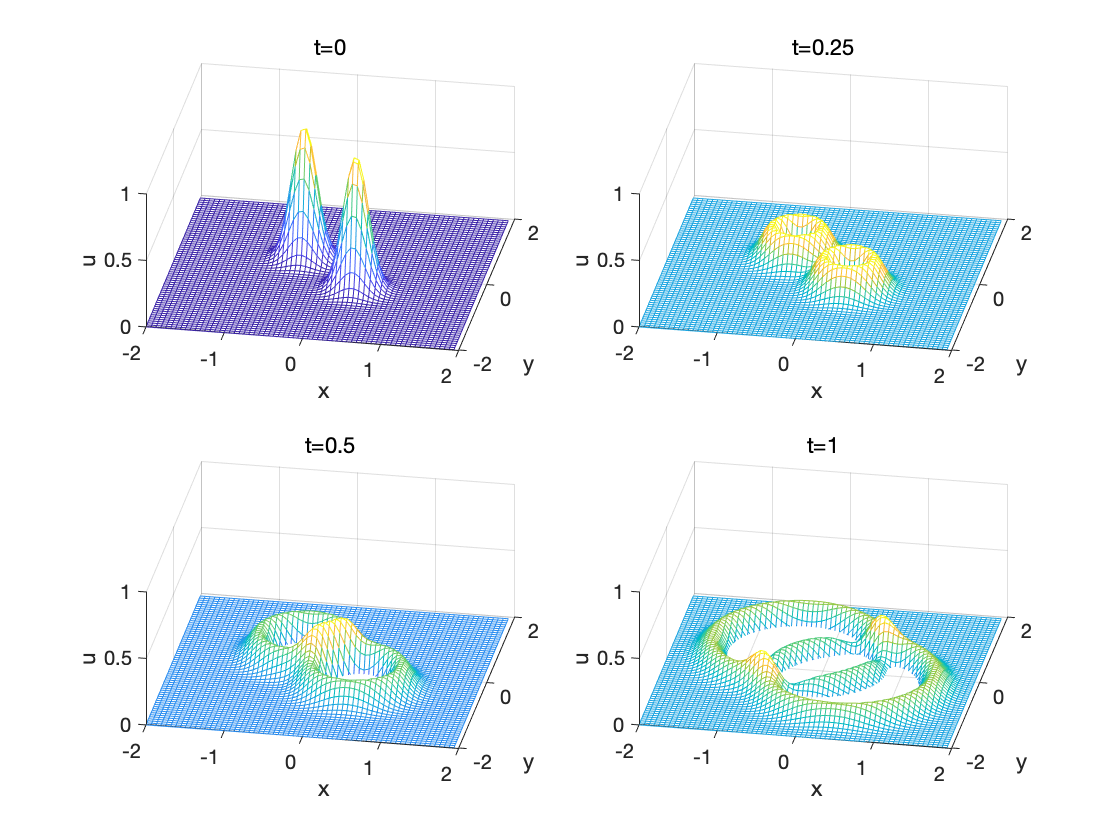
可以这样理解上述初始条件的物理意义: 两手抓住弹性薄膜的两个位置, 分别提起, 使薄膜上形成两个峰, 在 $t=0$ 时刻突然松手。根据生活常识可以预料到, 这两个位置的薄 膜将来回振动, 与此同时, 产生的波向四周传播, 而且波与波会在相遇处叠加。
为便于求解, 引入函数 $v$ 对式 $(1)$ 进行降阶, 得:
$$\{\begin{array}{l}\frac{\partial u}{\partial t}=v\\ \frac{\partial v}{\partial t}=a^2\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right)u\end{array}\text{\hspace{1em}(3)}$$

对上式等号两边做傅里叶变换, 得到常微分方程组:
$$\{\begin{array}{l}\frac{\partial \hat{\tilde{u}}}{\partial t}=\hat{\hat{v}}\\ \frac{\partial \hat{\hat{v}}}{\partial t}=-a^2\left(k_x^2+k_y^2\right)\hat{\hat{u}}\end{array}\text{\hspace{1em}(4)}$$
接下来用 ode45 求解即可, 代码如下:

主程序代码如下:

clear all; close all;

L=4;N=64;
x=L/N*[-N/2:N/2-1];y=x;
kx=(2*pi/L)*[0:N/2-1 -N/2:-1];ky=kx;
[X,Y]=meshgrid(x,y);
[kX,kY]=meshgrid(kx,ky);
K2=kX.^2+kY.^2;
% 初始条件
u=exp(-20*((X-0.4).^2+(Y+0.4).^2))+exp(-20*((X+0.4).^2+(Y-0.4).^2));
ut=fft2(u);vt=zeros(N);uvt=[ut(:); vt(:)];
% 求解
a=1;t=[0 0.25 0.5 1];
[t,uvtsol]=ode45('wave2D',t,uvt,[],N,K2(:),a);
% 画图
for n=1:4
    subplot(2,2,n)
    mesh(x,y,ifft2(reshape(uvtsol(n,1:N^2),N,N))),view(10,45)
    title(['t=' num2str(t(n))]),axis([-L/2 L/2 -L/2 L/2 0 1])
    xlabel x,ylabel y,xlabel x,zlabel u
end

文件 wave1D.m 代码如下:

function duvt=wave2D(t,uvt,dummy,N,K2,a)
ut=uvt(1:N^2);vt=uvt(N^2+[1:N^2]);
duvt=[vt;-a^2*K2.*ut];
end

程序输出结果如图所示, 它反映了弹性薄膜上的波向四周传播的过程。

最后

以上就是高大指甲油为你收集整理的Matlab傅里叶谱方法求解二维波动方程傅里叶谱方法求解基本偏微分方程—二维波动方程的全部内容，希望文章能够帮你解决Matlab傅里叶谱方法求解二维波动方程傅里叶谱方法求解基本偏微分方程—二维波动方程所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。