自抗扰控制器-６线性自抗扰控制器LADRC

二阶线性自抗扰控制器结构图如下图所示：

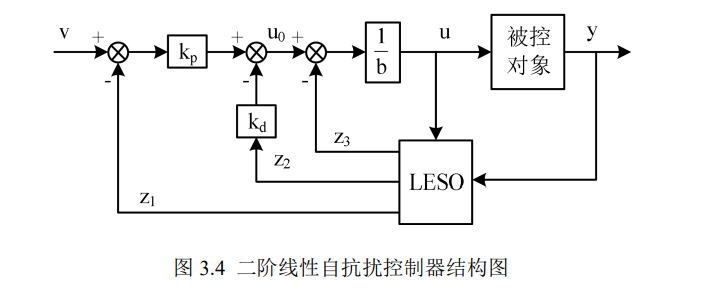
（1）线性扩张状态观测器
LESO 依然属于 LADRC 的中枢核心环节，而且 LESO 和 ESO 的功能基本
一致，都是针对系统“总扰动”进行实时反馈补偿。

设二阶不确定线性系统表达式如下：

上式中， f (x1, x2,wt)表示系统的总扰动，包含内部扰动和外部扰动， w(t)表示系统的外部扰动。

为了使得控制系统获得更好的稳定性能，减小调节时间，假设其理想特征方程为(s+w0 ) ^3=0，从而待整定参数u1、w2 和u3 与w0 可以有如下数学关系：u1=3w0 ,u2=3w0 ^2,u1=w0 ^3 . w0观测器带宽，其值会影响线性扩张状态观测器的观测精度，当选择较高值时，观测的精度也会提高，但是噪声信号也同样会被放大。因此，w0 值的选择应该充分考虑噪声对系统的影响。
（2）PD 线性控制组合
PD 线性控制组合实现的功能与跟踪微分器实现的功能相同，都是把输入信
号产生突变的区域转变为相对平稳的信号，降低了由于信号突变导致的超调，
同时改善了系统的运行性能。由图 3.4 可得 PD 线性控制组合数学表达式

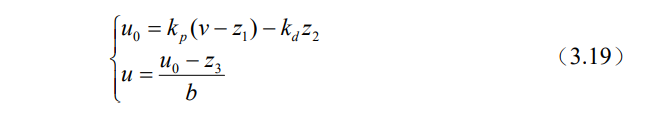
上式中，v 表示被控对象给定值；k p 和kd 分别表示 PD 线性控制组合的比例
系数和微分系数。与上文类似，假设其式（3.19）理想特征方程为(s+wc)^2 =0
从而待定参数 kp和 d k 与wc 可以有如下数学关系：kp=wc^2 kd=2wc 。wc 为控制器带宽，其值会影响控制器响应速度，当选择较高值时，其系统响应速度也越快，但是也增加了系统对于噪声信号的感知性，影响系统稳定。因此，wc 值的选择应该充分权衡系统快速性和稳定性需求。经过对非线性自抗扰控制器与线性自抗扰控制器的基本结构和应用原理分析可知，线性自抗扰控制器相对于非线性自抗扰控制器的结构更加简单，参数也由九个未知参数变成了观测器带宽w0 、控制器带宽wc 和补偿因子b 三个可调参数需要整定，大大减少了未知参数整定的工作量，同时控制器采用线性闭环控制系统，可以利用线性系统相关理论分析其稳定性和鲁棒性等问题，为理论分析带来便利。线性化自抗扰控制器的研究加快了非线性自抗扰控制器工业化的进程，使得其取代 PID 控制器成为可能。

最后

以上就是干净口红为你收集整理的自抗扰控制器-６线性自抗扰控制器LADRC的全部内容，希望文章能够帮你解决自抗扰控制器-６线性自抗扰控制器LADRC所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。