概述
CART
Classification & Regression Tree
1.熵（entropy）
对于一个取有限个值的随机变量X，如果其概率分布为：
P(X=xi)=pi,i=1,2,⋯,n
那么随机变量X的熵可以用以下公式描述：
H(X)=−∑i=1npilogpi
H(c)=p(c0)log2p(c0)+p(c1)log2p(c1)
事件发生的概率为1的时候，熵为0
基尼系数
Gini系数是一种与信息熵类似的做特征选择的方式，可以用来数据的不纯度。在CART(Classification and Regression Tree)算法中利用基尼指数构造二叉决策树。
Gini系数的计算方式如下：
2.条件熵（conditional entropy）
H(y|x)= H(x,y) - H(x)
条件熵=联合熵-熵
条件熵推导
继续p(x,y)可以分开写成
第二到第三行：p(x)*p(y|x)
第三到第四行：p(x)关于y无关，所以可以提到外面
3.互信息
定义：
当xy是离散
当xy是连续
互信息与边缘熵、条件熵、联合熵的关系：
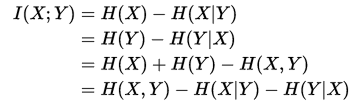
其中H(X)和H(Y) 是边缘熵，H(X|Y)和H(Y|X)是条件熵，而H(X,Y)是X和Y的联合熵。注意到这组关系和并集、差集和交集的关系类似，用Venn图表示：
于是，在互信息定义的基础上使用琴生不等式，我们可以证明 I(X;Y) 是非负的，因此H(X)>=H(X|Y)，这里我们给出 I(X;Y) = H(Y) - H(Y|X) 的详细推导:
4.相对熵
又称互熵、交叉熵、鉴别信息、Kullback熵，Kullback-Leible散度
p对q的相对熵：
最后
以上就是自由大雁为你收集整理的熵和基尼系数的全部内容，希望文章能够帮你解决熵和基尼系数所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复