CCF CSP 拼图 c++ 100分

这个题数据给的很庞大，显然需要快速幂。

想到了状压dp，但是不会写

经过学习别人的代码，自己写了份。

每一行的状态只与前一行有关

然后每行的状态我们可以通过状压，m最大为7，以1代表该格子已经填充了，以0代表还未填充，则每行的状态有2^7种。我们预先可以找到行与行之间的转移矩阵。

通过dfs，寻找转移矩阵。now是当前行的状态，从0遍历到2^m - 1,next是下一行的状态，index是当前行,即now的第index个方格，从0开始，到m-1。当index=m时，说明当前行已经填充满，此时的next的值，代表填充完now可以转移到的状态。

以下是四种转移情况（case1-4对应代码的相应部分）

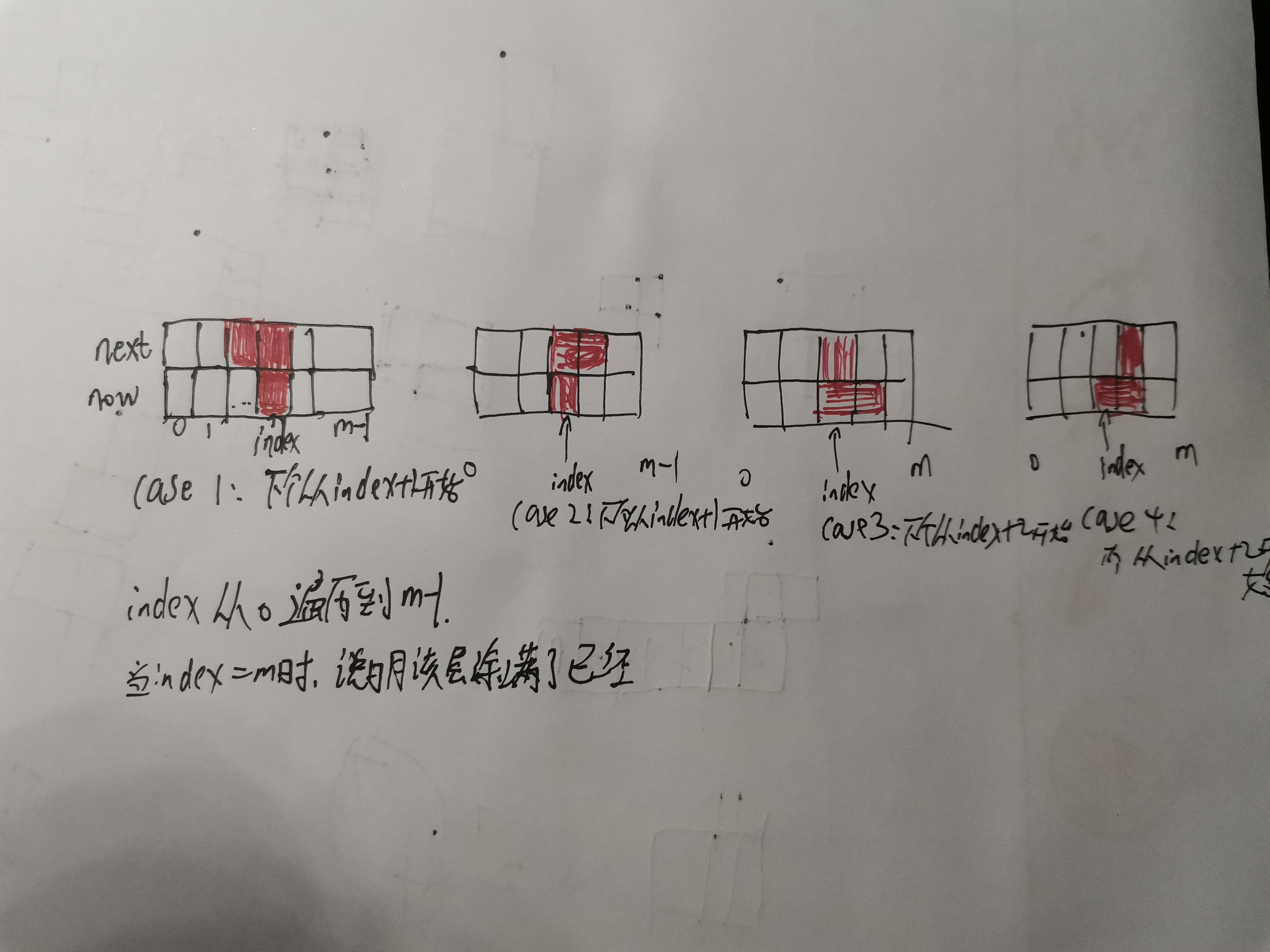
其中涉及到一些状压的位运算，比如!(next>>index&1),代表下一行的第index个放块尚未填充;next+(1<<index)，代表给next的第index个方块填充上。

完整代码如下

#include<iostream>

#include<vector>

#include<string>

#include<map>

#include<set>

#include<queue>

#include<algorithm>

#include<cstdio>

#include<cstring>

using namespace std;

typedef long long ll;

typedef pair<ll,ll> pa;

const int N=(1<<7)+5,mod=1e9+7;

int w[N][N];//转移矩阵

ll n,m;

void dfs(int now,int next,int index)

{   //now是当前行的状态,next是下一行的状态，index是第几列

    if(index==m){//index从0开始，到m了说明now已经排满了

        w[now][next]++;

        return ;

    }

    if(now>>index&1)dfs(now,next,index+1);//第index个位置已经放上了，不需要再安排了

    else{

        if(index&&!(next>>index&1)&&!(next>>index-1&1))//index代表不是0,即不是最左边 case1

            dfs(now,next+(1<<index)+(1<<index-1),index+1);

        if(index<m-1&&!(next>>index&1)&&!(next>>index+1&1))//case2

            dfs(now,next+(1<<index)+(1<<index+1),index+1);

        if(index<m-1&&!(now>>index+1&1)){

            if(!(next>>index&1))dfs(now,next+(1<<index),index+2);//case3

            if(!(next>>index+1&1))dfs(now,next+(1<<index+1),index+2);//case4

        }

    }

}

void multi(int a[][N],int b[][N],int c[][N])//矩阵乘法,a*b=c

{

    static int tmp[N][N];

    memset(tmp,0,sizeof(tmp));

    for(int i=0;i<1<<m;i++)

        for(int j=0;j<1<<m;j++)

            for(int k=0;k<1<<m;k++)

                tmp[i][j]=(tmp[i][j]+(ll)a[i][k]*b[k][j])%mod;

    memcpy(c,tmp,sizeof(tmp));

}

void qpow(ll x)//快速幂,x是指数

{   

    int ans[N][N];

    memset(ans,0,sizeof(ans));

    for(int i=0;i<N;i++)ans[i][i]=1;

    while(x){

        if(x&1)multi(ans,w,ans);

        multi(w,w,w);

        x>>=1;

    }

    //ans是转移矩阵的乘法

    //初态是只有[(1<<m)-1]是1

    cout<<ans[(1<<m)-1][(1<<m)-1]<<endl;

}

int main()

{

    cin>>n>>m;

    //求出转移矩阵

    for(int now=0;now<1<<m;now++)

        dfs(now,0,0);

    qpow(n);    

}

最后

以上就是纯情雪糕为你收集整理的CCF CSP 拼图 c++ 100分的全部内容，希望文章能够帮你解决CCF CSP 拼图 c++ 100分所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。