错题本——数据结构（图）

图

图中每个圆圈是一个补给站，存储着一定数量的汽油（在圈中标识），每个圈之间的路上标识了这段路需要消耗的汽油量，一辆小车从A点出发，在图上随意行走，到达某个补给站后，可以获得这个补给站的所有汽油，则其到B点后最多剩余的汽油量是____。（10）

解析：这道题考察的就是最小生成树的问题，首先我们可以先找到该图的最小生成树。

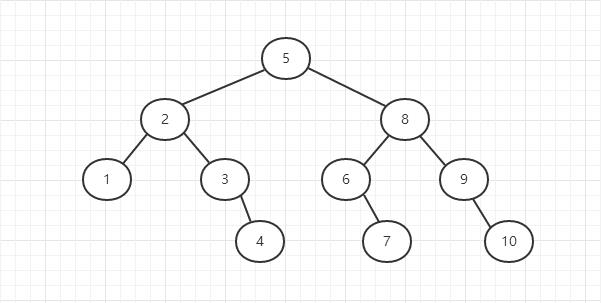
下列二叉树中，可能成为折半查找判定树（不含外部结点）的是( )。
A

B

C

D

解析：
折半查找判定树的生成：
向上取整：
第一层(第一次折半): (1-10)->5.5->6
第二层(第二次折半): 6左孩子(1-5)->3　6右孩子(7-10)->(8+9)/2=8.5->9
第三层(第三次折半): 3左孩子(1-2)->(1+2)/2=1.5->2　 3右孩子(4-5)->(4+5)/2=4.5->5　9左孩子(7-8)->(7+8)/2=7.5->8　9右孩子(10)->10
第四层(第四次折半): 2左孩子(1)->1　5左孩子(4)->4　8左孩子(7)->7

向下取整：

对于一个具有n个顶点的无向图，若采用邻接表表示，则表头向量的大小为_____。
n

解析：邻接表表头向量的大小即为顶点数

当各边上的权值(均相等)时,BFS算法可用来解决单源最短路径问题

解析：若所有边权值相等时，BFS算法返回的解一定是距离根节点经过边最少的路径，因此也是最短路径。

设 d=(d1,d1,…dn)，其中 di为非负整数，i=1,2,…n 。若存在n个顶点的(简单)无向图,使得顶点vi的度为 di，则称 d是可图解的。下面给出的各序列中哪个是可图解的？
A (0，1，1，2，,3，3)；
B (1，1，2，2，3);
C (0，1，3，3，3)；
D (1，3，4，4，5)。

解析：
可图解就是可图化
1：非负整数d=(d1,d1,…dn)是可图化的当且仅当 ∑di （i:1…n）为偶数
所以，先排除B,D
2：若n阶无向简单图，则∆（G）<=n-1 （∆（G）：无向图的最大度）
因为A,C都满足这两个条件，然后，就只能通过画图判断，很容易就知道，C选项是不可能的（画不出来）。

已知无向图G含有16条边，其中度为4的顶点个数为3，度为3的顶点个数为4，其他顶点的度均小于3。图G所含的顶点个数至少是 （11）。

解析：
无向图度的总和等于边数的两倍，设度小于3 的顶点数为$x$，度为$y$，于是可以得方程$12+12+xy=32$，即$xy=8$，当$y=2$时，$x$取得最小值。

有ABCDEF 六个城市，每一个城市都和其他所有城市直接相连，问从A——B有多少种连接方式，路径不允许在两个城市之间往返
答：65

解析:
A-B:1
A-?-B:4
A-?-?-B:4*3
A-?-?-?-B:4*3*2
A-?-?-?-?-B:4*3*2*1

一个含有n个顶点的连通且无环的简单无向图，在其临接矩阵存储结构中共有多少个零元素？
答：$n^2-n+2$

解析：
n个顶点的连通图至少有n-1条边

图的BFS生成树的树高比DFS生成树的树高()
答案：小或等于

无向图的邻接矩阵可用一维数组存储。（）
答案：正确

解析：任意二维数组都是可以用一维数组存储的，只是使用起来不太方便

假设以邻接表作为图的存储结构，则按深度优先遍历该图所得到生成树是唯一的。
答案：错误

解析：可以认为按照邻接表DFS遍历的结果是唯一的，但是生成的邻接表不一定是唯一的，因此回溯的时候并不能得到唯一的遍历结果

邻接多重表是无向图和有向图的链式存储结构。（ ）
答案：错误

解析：无向图特有：连接多重表；有向图特有：十字链表

具有7个顶点的有向图至少应有多少条边才可能成为一个强连通图?
答案：7

解析：
强连通图必须从任何一点出发都可以回到原处，故由 n 个顶点的强连通图最多有 n(n-1) 条边，最少有 n 条边。

给定一个如下所示的图，图中的边代表了两个节点间的距离。如果使用迪杰斯特拉算法对节点 1 和节点 8 求最短路径，则当完成计算时，算得节点 1 到节点 8 的最短路径是？同时当完成节点 1 到节点 8 的最短路径计算时，节点 1 到哪些节点（除了 1 和 8 ）的最短路径也已经计算完毕？（　）

答案：最短路径：４；已经算得最短路的节点：２，３，５，４

解析：
初始状态：路径长度0：（1）
路径长度1：（1,5）
路径长度2：（1,3）
路径长度3：（1,3,4），（1,2）
路径长度4：（1,5,8）

p个顶点p条边的连通图中至少有多少个生成树？
A. 2
B. 3
C. 4
D. p
答案：B

解析：

某软件系统结构图如图所示，该结构图的深度为（）。

答案：3

解析：
D和BCE是同一层，CE都是指向兄弟节点

如果有向图的拓扑排序序列是唯一的,则图中必定只有一个顶点的入度为0,一个顶点的出度为0
答案：正确

解析：
如果有向图的拓扑排序序列是唯一的时候，说明各个顶点已经排在一个线性有序的序列中，每个顶点都有唯一的前驱后继关系。这就说明有首有尾，第一个顶点入度为0，最后一个顶点出度为0. 另外，这只是个必要条件，只有一个顶点的入度为0,一个顶点的出度为0不一定能得出唯一的拓扑排序

在下图的多边形ABCDE中从哪一点出发，可以遍历图上的每条边一次，而且仅遍历一次。

答案：B点

解析：
这是寻找欧拉回路问题
无向图中，G有欧拉通路的充分必要条件为：G连通，G中只有两个奇度顶点(它们分别是欧拉通路的两个端点)

连通分量是无向图中极小连通子图
答案：错误

解析：
无向图G的极大连通子图称为G的连通分量

面关于求关键路径的说法不正确的是（）。
A 求关键路径是以拓扑排序为基础的
B 一个事件的最早开始时间同以该事件为尾的弧的活动最早开始时间相同
C 一个事件的最迟开始时间为以该事件为尾的弧的活动最迟开始时间与该活动的持续时间的差
D 关键活动一定位于关键路径上
答案：C

解析：
做这题要注意几点概念：
1）顶点表示事件，弧表示活动
2）如果顶点A->B有弧，如果让弧表示为L，则A为L的弧尾，B为L的弧头，即有箭头的那一端叫头。
一个事件的最早开始时间同以该事件为尾的弧的活动最早开始时间相同
一个事件的最迟开始时间为以该事件为头的弧的活动最迟开始时间与该活动的持续时间的差

对于以下说法，错误的是________。
A Dijkstra算法用于求解图中两点间最短路径，其时间复杂度O(n^2)
B Floyd-Warshall算法用于求解图中所有点对之间最短路径，其时间复杂度为O(n^3)
C 找出n个数字的中位数至少需要O(nlogn)的时间
D 基于比较的排序问题的时间复杂度下界是O(nlogn)
答案：C

解析：
利用顺序统计思路找出n个数字的中位数可以在$O(n)$时间内完成

补充
Dijkstra求解图最短路径的复杂度与所选的数据结构有关，如果用数组，则为$O(n^2)$，若选用二叉堆，则为$O(elogn)$，若选用Fibonacci堆，则为$O(e+nlogn)$

给定6个小区之间的交通图。若小区i与小区j之间有路可通，则将顶点i与顶点j之间用边连接，边上的权值表示这条道路的长度。现在打算在这n个小区中选定一个小区建一所医院。这家医院应建在小区（），才能使距离医院最远的小区到医院的路程最短？
注：图为无向图。

答案：B

解析：

n个顶点的无向图的邻接表最多有()个边表结点
A n^2
B n(n-1)
C n(n+1)
D n(n-1)/2
答案：B

解析：
有n个顶点的无向图最多有n*(n-1)/2条边，此时为完全无向图，而在邻接表中每条边存储两次，所以有n*（n-1)个结点

以下哪个数据结构不是多型数据类型()
A 栈
B 广义表
C 有向图
D 字符串
答案：D

解析：
多型数据类型是指包含的数据元素的类型并不确定

一个直线将一个平面分成 2 部分，两条直线分成 4 部分，如果直线不平行，多条直线不共一点，问 100 条直线将平面分成几部分？
答案：5051

解析：
1条直线,将平面分成2个区域
2条直线,将平面分成2+2个区域
3条直线,将平面分成2+2+3个区域
4条直线,将平面分成2+2+3+4个区域
5条直线,将平面分成2+2+3+4+5个区域
故n条直线,将平面分成2+2+3+4+5+…+n个区域，即n(n+1)/2+1

设G是一个具有6个顶点,11条边的图，其每个顶点的度为3或4，则图G是什么图？
A G是平面图；
B G不连通；
C G为偶图(也称二部图)；
D G不是哈密顿图。
答案：A

解析：
偶图（二部图/二分图）：顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集，两个子集内的顶点不相邻。判断方法：用染色法，把图中的点染成黑色和白色。首先取一个点染成白色，然后将其相邻的点染成黑色，如果发现有相邻且同色的点，那么就退出，可知这个图并非二分图。

哈密尔顿图就是不重复过顶点但可一次过完所有顶点的图，判断方法：图中任意两点度的和大于或等于顶点总数，那这个图一定是哈密顿图

图示是一个网络流从s到t的某时刻快照。此时t处一共接收到10+13+16=39单位流量。每条横线上的数字表示当前流量和管道的容量。那么，该网络最大的流量是多少？
答案：41

解析：



关于最大流的问题，详细参见《算法导论》

一个非连通图(无自回路和多重边)有66条边,那么它至少有()个顶点
A 11
B 12
C 13
D 14
答案：C

解析：
对无向图来说，完全图边和顶点满足 $e=n(n-1)/2$
故，对A来说，只需要55条边就构成完全图，对B来说，刚好构成完全图

即使有向无环图的拓扑序列唯一,也不能唯一确定该图()
答案：错

解析：

在图G的最小生成树G1中，可能会有某条边的权值超过未选边的权值.
答案：正确

用邻接表存储图所用的空间大小()
答案：与图的顶点数和边数都有关系

解析：
无向图 $O(V+2E)$
有向图 $O(V+E)$

在工程网络计划中，工作 M 的最早开始时间为第 16 天，其持续时间为 5 天。该工作有三项紧后工作，他们的最早开始时间分别为第 25 天、第 27 天和第 30 天，最迟开始时间分别为第 28 天、第 29 天和第 30 天。则工作 M 的总时差为（）天。
答案：7

解析：
工作M的最迟开始时间为第23天（23+5=28，第28天要开始另外的工作了，所以最晚必须第23天开始），最早开始时间为第16天，所以总时差有7天

最早完成工作M的时间是第21天，下次项目开始的最早是第25天，所以自由时差是25-21=4天。
（自由时差，简称FF（Free Float），指一项工作在不影响其紧后工作最早开始时间的条件下，本工作可以利用的机动时间。 ）

总时差就是拖拖拖，可以拖多少天才做工作M，自由时差就是早早完成，然后在下次工作委派之前可以休息多少天。

关键路径算法可参考： 关键路径核心算法

要保证连通具有10个顶点的无向图，至少需要（）条边。
答案：37

解析：
题目的意思是说不管怎么胡连，这个图都是连通的，故 $\frac{(n-1)(n-2)}{2}+1$

若一个有向图具有有序的拓扑排序序列,那么它的邻接矩阵必定为()
正确答案: C
对称矩阵
稀疏矩阵
三角矩阵
一般矩阵

解析：
注意题目题目问的是有序的

位示图法可用于 。
正确答案: C
文件目录的查找
分页式存储管理中主存空闲块的分配和回收
磁盘空闲盘块的分配和回收
页式虚拟存储管理中的页面置换

解析：
位示图是利用二进制的一位来表示磁盘中的一个盘块的使用情况。当其值为“0”时，表示对应的盘块空闲；为“1”时，表示已经分配

用相邻矩阵A表示图，判定任意两个顶点Vi和Vj之间是否有长度为m的路径相连，则只要检查（ ）的第i行第j列的元素是否为零即可。
正确答案: B 你的答案: D (错误)
A
A^m
Am-1
mA

解析：
m不是权，

图G是n个顶点的无向完全图,则下列说法正确的有:()
正确答案: B C D
G的邻接多重表需要n(n-1)个边结点和n个顶点结点
G的连通分量个数最少
G为连通图
G所有顶点的度的总和为n(n-1)

解析：
A 需要$\frac{n(n-1)}{2}$个边界点

补充
一个有n个节点的图，最少有1个连通分量，最多有n个连通分量
解析：最少是1个，这种情况下，它本身就是一个连通图；最多是n个，这种情况下，它由n个分散的点组成的一个图

连通分量：在无向图中，如果从顶点vi到顶点vj有路径，则称vi和vj连通。如果图中任意两个顶点之间都连通，则称该图为连通图，否则，将其中的较大连通子图称为连通分量。

强连通分量：在有向图中，如果对于每一对顶点vi和vj，从vi到vj和从vj到vi都有路径，则称该图为强连通图；否则，将其中的极大连通子图称为强连通分量。

一个无向图 G=(V,E) 是连通的，那么边的数目大于等于顶点的数目减一：|E|>=|V|-1，而反之不成立。

如果 G=(V,E) 是有向图，那么它是强连通图的必要条件是边的数目大于等于顶点的数目：|E|>=|V|，而反之不成立。

没有回路的无向图是连通的当且仅当它是树，即等价于：|E|=|V|-1。

最后

以上就是玩命发卡为你收集整理的错题本——数据结构（图）的全部内容，希望文章能够帮你解决错题本——数据结构（图）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。