一、图像噪声概要

1. 图像噪声的产生主要源于两个方面：

• 图像获取过程中

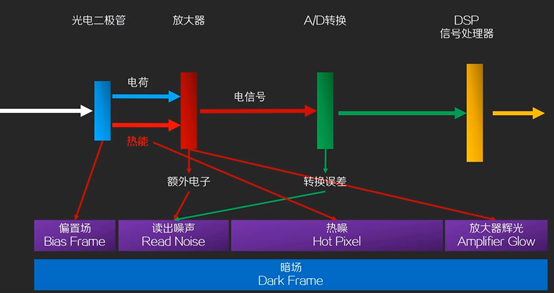
常见的图像传感器CCD和CMOS在采集图像过程中，由于受到工作环境或者电子电路结构的影响，会引入各种噪声，如热噪声、光子噪声、暗电流噪声等。

• 信号传输过程中

由于传输介质和记录设备等的不完善，或者受到外部环境的干扰，数字图像在其传输记录过程中往往会受到多种噪声的污染。

2. 噪声的分类

• 加性噪声模型
  产生机制是粉尘的遮挡或者采集元器件的损坏以及传输过程中数据的丢失等等
• 乘性噪声模型
  在自然图像中由于一些光照等因素的影响，导致原始信号中的像素值成倍数的改变，在这个模型中，噪声信号被乘以原始信号，信号在它在，信号不在他也就不在。

3. 常见噪声种类

图像常见噪声基本上有以下四种：高斯噪声，泊松噪声，乘性噪声，椒盐噪声

3.1 高斯噪声

高斯噪声是指它的概率密度函数服从高斯分布（即正态分布）的一类噪声。如果一个噪声，它的幅度分布服从高斯分布，而它的功率谱密度又是均匀分布的，则称它为高斯白噪声。高斯白噪声的二阶矩不相关，一阶矩为常数，是指先后信号在时间上的相关性。

产生原因：
1）图像传感器在拍摄时市场不够明亮、亮度不够均匀；
2）电路各元器件自身噪声和相互影响；
3）图像传感器长期工作，温度过高。

使用python代码模拟高斯噪声：

def gasuss_noise(image, mean=0, var=0.001):
    '''
        添加高斯噪声
        mean : 均值
        var : 方差
    '''
    image = np.array(image/255, dtype=float) # image/255是将矩阵归一化到[0.1]
    noise = np.random.normal(mean, var ** 0.5, image.shape)
    out = image + noise
    if out.min() < 0:
        low_clip = -1.
    else:
        low_clip = 0.
    out = np.clip(out, low_clip, 1.0) # 将数组out中的所有数限定到范围[low_clip，1]中
    out = np.uint8(out*255)
    return out

3.2 椒盐噪声

椒盐噪声，椒盐噪声又称脉冲噪声，它随机改变一些像素值，是由图像传感器，传输信道，解码处理等产生的黑白相间的亮暗点噪声。

代码模拟椒盐噪声：

def sp_noise(image,prob):
    '''
    添加椒盐噪声
    prob:噪声比例
    '''
    output = np.zeros(image.shape,np.uint8)
    thres = 1 - prob
    for i in range(image.shape[0]):
        for j in range(image.shape[1]):
            rdn = random.random()
            if rdn < prob:
                output[i][j] = 0
            elif rdn > thres:
                output[i][j] = 255
            else:
                output[i][j] = image[i][j]
    return output

3.3 泊松噪声

泊松噪声，就是符合泊松分布的噪声模型，泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。

def poisson_noise(image,lam):
    '''
         添加泊松噪声
     '''
    image = np.array(image / 255, dtype=float)  # image/255是将矩阵归一化到[0.1]
    noise = np.random.poisson(lam, image.shape)
    out = image + noise
    if out.min() < 0:
        low_clip = -1.
    else:
        low_clip = 0.
    out = np.clip(out, low_clip, 1.0) # 将数组out中的所有数限定到范围[low_clip，1]中
    out = np.uint8(out*255)
    return out

3.4 乘性噪声

乘性噪声一般由信道不理想引起，它们与信号的关系是相乘，信号在它在，信号不在他也就不在。

4. 图像评价标准

去噪处理后图像的评价指标用$PSNR$（峰值信噪比）来客观评价：
$$PSNR=10\cdot {log}_{10}\left(\frac{MA{X}_I^2}{MSE}\right)$$
其中$MSE$为均方误差：
$$MSE=\sum _{i=0}^{n-1}\sum _{j=0}^{m-1}{\left[I\left(i,j\right)-K\left(i,j\right)\right]}^2$$

二、传统去噪算法

1. 传统去噪算法主要分类

• 空间域去噪算法
  该类算法主要是在空间中进行去噪，将图像看做二维或者三维矩阵，噪声就是矩阵中元素数值比较突兀的部分，利用矩阵的相关运算对这些突兀的部分进行处理，从而达到去噪的目的。
• 频域去噪算法
  这类算法主要是将图像通过某些变换（傅里叶变换、小波变换等）转换到频域上，噪声就是频域中峰值比较高的点，在频域中将这些峰值高的地方做均匀化处理，最后把频域通过逆变换转换到空间域上，从而完成去噪的工作。

2. 常见去噪算法

2.1 均值滤波

均值滤波中，滤波器中每个像素的权重是相同的，即滤波器是线性的。均值滤波用像素邻域的平均灰度来代替像素值，适用于脉冲噪声。从频率域观点来看均值滤波是一种低通滤波器，高频信号将会去掉，因此可以帮助消除图像尖锐噪声，实现图像平滑，模糊等功能。

imag = cv2.blur(src,ksize=(w,h))
# src为输入图像
# ksize为滤波器大小

2.2 高斯滤波

高斯滤波矩阵的权值，随着与中心像素点的距离增加，而呈现高斯衰减的变换特性。这样的好处在于，离算子中心很远的像素点的作用很小，从而能在一定程度上保持图像的边缘特征。

imag = cv2.GaussianBlur(src,ksize=(5,5),sigmaX=1.5)
# src是输入图像
# ksize是滤波器大小
# sigmaX X方向上的高斯核标准差
# sigmaY Y方向上的高斯核标准差

2.3 中值滤波

中值滤波器是一种非线性滤波器，首先确定一个滤波窗口及位置，然后将窗口内的像素值按灰度大小进行排序，最后取其中位数代替原窗口中心的像素值。对椒盐噪声表现较好，但是对流量、速度等快速变化的参数不宜。

imag = cv2.medianBlur(src,ksize=5)
# src是输入图像
# ksize是滤波窗口大小

3、传统的去噪算法

3.1 NLM算法

非局部均值滤波(Non-Local Means,NLM)是Buades等人于2005年在论文“A non-local algorithm for image denoising”中提出。

基本原理：假设同一副图像上，有着很多相似的纹理；因此在有噪声的区域，可以通过将相似的纹理区域来替换噪声区域从而达到去噪目的。

1、该算法需要遍历整个原图像：首先取出一个原图像pixel，以该pixel坐标为中心，圈出一大、一小两个矩形。大的矩形表示纹理替换搜索区域$R$，小的矩形表示待处理pixel的纹理区域$L$。
2、将$R$矩形区域，分成若干个和$L$矩形区域一样的大小的矩形$L_i$。计算出每块$L_i$和$L$之间的权重$W$。
3、将$L$的像素值都设置为0，然后根据$L$与每块$L_i$的权重$W$，叠加当前$L$的像素值为：$W\times L_i$。
4、将$L$和每块$L_i$之间的权重$W$，同样累加起来到$W_{all}$。
5、所有$L_i$遍历完了之后，$L=\frac{L}{W_{all}}$，就得到了经过去噪处理之后的$L$区域像素。

代码实现：

# 自定义实现
def NLmeansfilter(image, L, h_=10, templateWindowSize=5, searchWindowSize=11):
    global I_1
    image = image.astype(np.float64)
    f = int(templateWindowSize / 2)
    t = int(searchWindowSize / 2)
    height, width = image.shape[:2]  # 利用ndarray的索引得到长宽
    padLength = t + f
    I2 = np.pad(image, padLength, 'symmetric')  #symmetric——表示对称填充，每侧填充均为padLength
    kernel = make_kernel(f)
    h = (h_ ** 2)
    I_ = I2[padLength - f:padLength + f + height, padLength - f:padLength + f + width]

    average = np.zeros(image.shape)
    sweight = np.zeros(image.shape)
    w_max = np.zeros(image.shape)
    for i in range(-t, t + 1):
        for j in range(-t, t + 1):
            if i == 0 and j == 0:
                continue
            I2_ = I2[padLength + i - f:padLength + i + f + height, padLength + j - f:padLength + j + f + width]
            w = np.exp(-cv2.filter2D((I2_ - I_) ** 2, -1, kernel) / h)[f:f + height, f:f + width]
            sweight += w
            w_max = np.maximum(w_max, w)
            average += (w * I2_[f:f + height, f:f + width])
            I_1 = (average + w_max * image) / (sweight + w_max)
    return np.clip(np.round(I_1), 0, 255).astype(L.dtype)

# 利用opencv自带的NLM去噪
R2 = cv2.fastNlMeansDenoising(image,dst=None,templateWindowSize=5, searchWindowSize=11)

3.2 BM3D算法

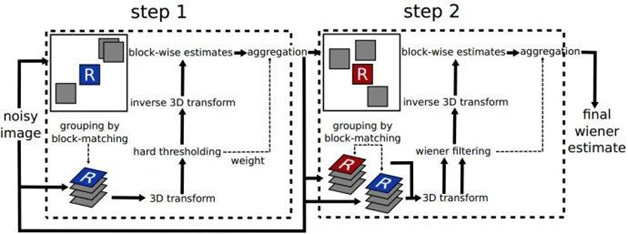
BM3D算法先吸取了空间域去噪算法中的计算相似块的方法，然后又融合了小波变换域去噪的方法。其主要步骤分为基础估计和最终估计，在这两大步中，分别又有三小步：相似块分组，协同滤波和聚合。
在基础估计中，第一步相似块分组的主要任务是在噪声图像中选择一些像素块作为参考，然后在这些像素块周围适当区域进行搜索，找到与选择的像素块最相似的块，并把这些相似的块叠加成一个三维矩阵。第二步协同滤波的任务是将分组的若干三维矩阵块通过小波变换转换到频域上，将小于设定阈值的系数置0，即频域滤波，然后再通过逆小波变换得到处理后的像素块。最后一步聚合，是将分组处理后的像素块通过一定加权融合到其原来的位置上，这时像素块的值是对噪声图像的估计。
最终估计的流程与基础估计大致相同，也是第一步相似块分组，不过这时的相似块分组会考虑到基础估计中相似块分和聚合后的结果，第二步协同滤波时使用了用维纳滤波（Wiener Filtering）代替了硬阈值处理，第三步将三维像素块加权融合，得到对噪声图像的最终估计，也就完成了图像去噪任务。

最后

以上就是可耐猎豹为你收集整理的图像的去噪一、图像噪声概要二、传统去噪算法的全部内容，希望文章能够帮你解决图像的去噪一、图像噪声概要二、传统去噪算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。