【算法导论】插入排序与归并排序学习目标：学习内容：学习总结

103 阅读 0 评论 68 点赞

我是靠谱客的博主慈祥大白，最近开发中收集的这篇文章主要介绍【算法导论】插入排序与归并排序学习目标：学习内容：学习总结，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

学习目标：

学习插入排序和归并排序

学习内容：

插入排序
归并排序
二者对比

1.插入排序

输入：n个数的一个序列<a1,a2,...,an>

输出：输入序列的一个排列<a1',a2',...,an'>,满足a1'<=a2'<=...<=an'

输入是以n个元素的数组的形式出现的

其伪代码如下所示：

for j=2 to A.length
    key=A[i]//在A[1..j-1]序列中插入A[j],其中key为关键词是希望排序的数
    i=j-1
    while i>0 and A[j]>key
          A[i+1]=A[i]
          i=i-1
    A[i+1]=key

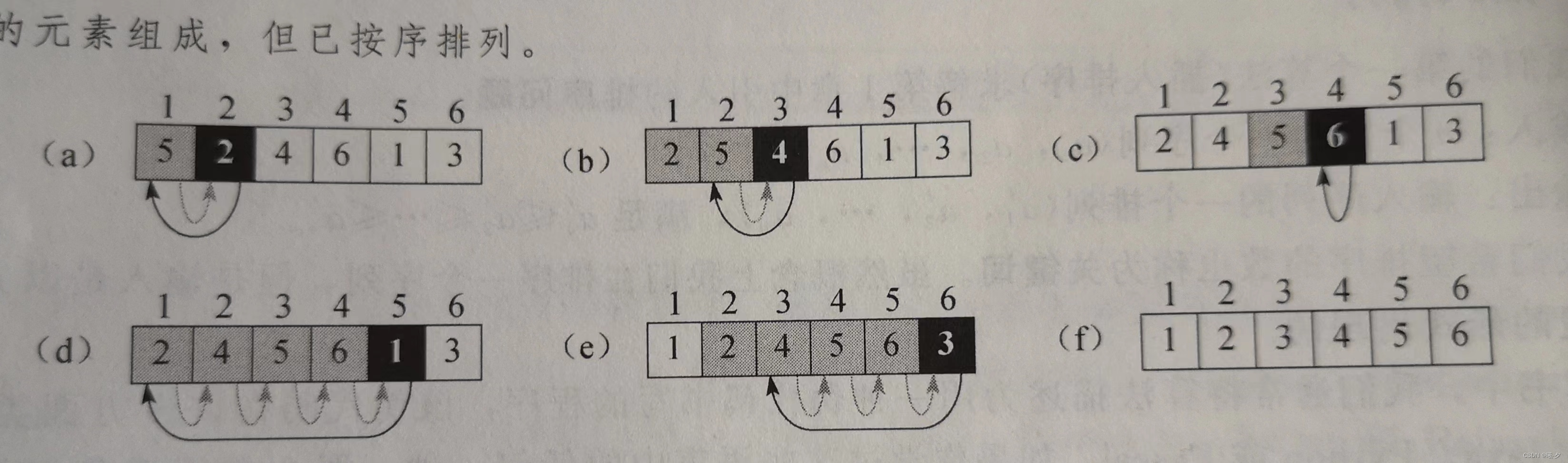
下图表明了该算法如何工作

我们把需要排列的数组的性质形式地表示为循环不变式，即在每次迭代开始时，子数组由原来数组中的元素组成，但都已按序排列

2.归并排序

归并排序遵循分治，将原问题分解为几个子问题，再求解子问题，最后合并子问题的解

例如：有一个数组A=[4,3,7,9,2,5,10,6]

首先把数组A分成两个子数组a1=[4,3,7,9],a2=[2,5,10,6],将其按顺序排列好新的子数组a1'=[3,4,7,9],a2'=[2,5,6,10]，然后分别用首位进行对比较小的一个放入新的数组A’中，然后再用两个新子数组的首位对比，以此类推，就得到了A‘=[2,3,4,5,6,7,9,10]

其伪代码如下所示：

n1=q-p+1
n2=r-q
let L[1..n1+1] and R[1..n2+1] be new arrays
for i=1 to n1
    L[i]=A[p+i-1]
for j=1 to n2
    R[j]=A[q+j]
L[n1+1]=∞
R[n2+1]=∞
i=1
j=1
for k=p to r 
    if L[i]<=R[j]
    A[k]=L[i]
    i=i+1
else A[k]=R[j]
    j=j+1

3.对比

在大概了解了插入排序和归并排序以后，那么两者的区别在哪呢？

是运行时间。算法的运行时间依赖诸多因素，输入本身就是一个因素，这里还要说的一个就是输入规模

对于插入排序来说，运行时间是每条语句运行时间之和，所以该算法分为两种情况：第一种是最佳情况，此时，输入的数组已经排好序列，时间与数组中元素的个数n成线性函数T(n)=an+b,则T(n)=Θ(n)；第二种是最坏的情况，此时，输入的数组是反向排序，时间与数组中元素的个数n成二次函数T(n)=an^2+bn+c，则T(n)=Θ(n^2)，这种情况也是运行时间的一个上界

注：Θ为渐近符号，需忽略函数的低阶项和重要项的系数

对于归并排序来说，也有两种情况，第一种是n为一时，此时的运行时间为常数，即为Θ(1)；第二种是n大于一时，这里假设将原问题分解为2个规模为n/2的子问题，那么求解一个子问题所需的时间为T(n/2)，两个子问题也就是2T(n/2)，合并和分解问题的时间需要Θ(n)+Θ(1)，所以它的总的运行时间也就是T(n)=2T(n/2)+Θ(n)（因为Θ(n)+Θ(1)得到的是线性函数，所以结果为Θ(n)）

将T(n)=2T(n/2)+Θ(n)更改为T(n)=2T(n/2)+cn，通过递归树我们可以得到T(n)=cnlgn+cn，即T(n)=Θ(nlgn)(这里的递归树后续在详细说明)

因此，当规模足够大时，Θ(nlgn)比Θ(n^2)要快，归并排序优于插入排序；当规模很小时，插入排序会更好。（这里的界限大概在30）