内卷之源:
https://leetcode.cn/problems/path-sum-iii/
题目描述:
* 给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
* 路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
* 说明:
二叉树的节点个数的范围是 [0,1000]
-10^9 <= Node.val <= 10^9
-1000 <= targetSum <= 1000
测试用例:
| Input | Output |
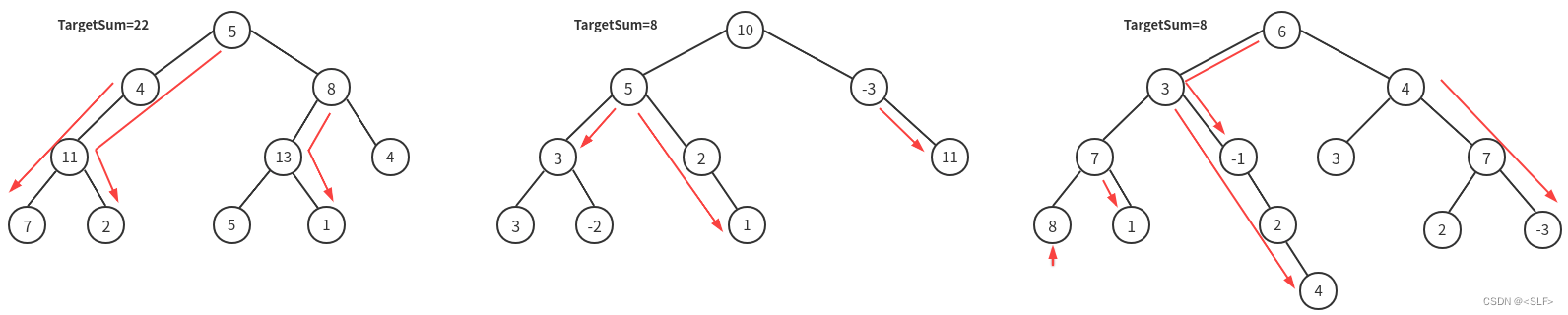
| root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 | 3 |
| root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 | 3 |
| root = [6,3,4,7,-1,3,7,8,1,null,2,null,null,2,-3,null,null,null,null,nul,null,null,4], targetSum = 8 | 5 |
| root = [8], targetSum = 8 | 1 |
| root = [null], targetSum = 12 | 0 |
本题三个输入示例对应的二叉树如下:
思路分析:
法一:穷举所有的可能。
使用 深度优先搜索 + 前序遍历方法 以任意节点node为起始节点,检测向下延深满足要求的路径有多少种。实际是一个递归做加法的过程,由于节点的元素可以为负数,所以当前面节点之和满足要求时,仍可以继续累加后面节点,直到叶子节点。
逐节点递归遍历,将加入当前节点后是否满足要求的判断结果作为递归函数的返回值,然后将这些返回值求和即可得到总的路径数。
该方法有两层递归:一是刚提到的递归做加法过程,二是选取路径起始节点。
法二:前缀和——根节点到当前节点的路径上所有节点的和。
使用 深度优先搜索 + 前序遍历方法 保存各节点的前缀和。若当前节点P_curr的前缀和 减去 targetSum 的差值,等于当前节点所在路径前面某一节点P_i的前缀和,则从P_(i+1)到P_curr的节点值之和必然等于 targetSum。
本地自测Demo根据输入序列构造二叉树:
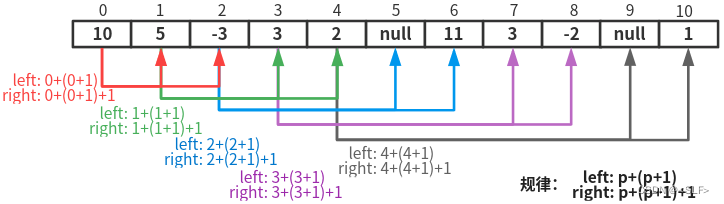
由于输入序列不是前中后序任意一种,而是按从上往下、同层从左至右的顺序(即Z字形),且空节点用null表示。该格式序列很容易手画二叉树,但如何用程序实现却不容易。回想 从前序与中序遍历序列构造二叉树 按从上往下、同层从左至右逐层打印二叉树(空节点用null表示)的思路,其输出序列格式与本例的输入序列格式一致,似乎可以借鉴其处理逻辑。实际确实可行,只是还需考虑各节点在输入序列中的索引位置,因为各节点对应的左右子树在序列中的位置是可以计算得到的(类似堆排序算法堆积树左子节点及其父节点的处理),如下图所示
编程实现(C++):
/*
************************************************************
* @author SLF
* @version V1.0.0
* @date 7-July-2021
************************************************************
*/
#include <iostream>
#include <vector>
#include <queue>
#include <utility> //pair
#include <unordered_map>
#include <memory>
// #include <cmath> //pow()
#define METHOD_PREFIX (0)
#define METHOD_EXHAUSTIVITY (1)
#define DUMMY_NULL 0x7FFFFFFF
using namespace::std;
typedef struct TreeNode {
TreeNode():val(0),left(nullptr),right(nullptr) {}
TreeNode(const int v):val(v),left(nullptr),right(nullptr) {}
TreeNode(const int v, shared_ptr<TreeNode> l, shared_ptr<TreeNode> r):val(v),left(l),right(r) {}
int val;
shared_ptr<TreeNode> left;
shared_ptr<TreeNode> right;
}TreeNode;
class Solution {
private:
/**
* 前缀和方法
* 时间复杂度:O(N),只需按节点数量递归遍历一次即可
* 空间复杂度:O(N),容器 preSum 只存储了最多节点数量个不同累加和值
**/
int prefixSumMethod(const shared_ptr<TreeNode> root, long long recursiveSum, const int targetSum)
{//深度优先搜索dfs
if(!root)
{//空节点
return 0;
}
int path = 0;
//逐节点累加
recursiveSum += root->val;
//在存入unordered_map容器前判断 当前累加和 减去 targetSum 的 差 是否存在unordered_map中
if(preSum.count(recursiveSum - targetSum))
{//存在unordered_map中(unordered_map的key是按递归深度递增的节点累加和值),即去掉 该条路径上根节点到前面某节点的累加和恰为该差值的那些节点,剩余的节点即可组成符合要求的路径(要注意以二叉树根节点为起始且符合要求的路径,不需要去掉节点,且该路径此处差值恰为0,所以pathSum()函数中才会单独赋值处理)
path = preSum[recursiveSum - targetSum]; //1(当前路径中) 或 0(先前其它路径加入unordered_map)
}
//继续累加子树中的节点(不是基于节点值可为负数的考虑,而是上面的判断是可将该路径前端节点去掉)
preSum[recursiveSum]++;
//前序遍历
path += prefixSumMethod(root->left, recursiveSum, targetSum);
path += prefixSumMethod(root->right, recursiveSum, targetSum);
//每条路径的累加和已使用,故减掉一次(减的过程肯定是从最长路径逐渐到最短路径),否则会影响其它路径
preSum[recursiveSum]--;
return path;
}
/**
* 穷举法
* 时间复杂度:O(N^2),选取路径起始节点遍历一次,检索路径遍历一次
* 空间复杂度:O(N),虽然不像前缀和那样使用容器,但递归需要栈空间
**/
int exhaustiveMethod(const shared_ptr<TreeNode> &root, const int targetSum)
{//深度优先搜索dfs
if(!root)
{//空节点
return 0;
}
int path = 0;
//使用当前节点作为路径起始节点
path = exhaustivePath(root, 0, targetSum);
//前序遍历,选取路径起始节点
path += exhaustiveMethod(root->left, targetSum);
path += exhaustiveMethod(root->right, targetSum);
return path;
}
int exhaustivePath(const shared_ptr<TreeNode> &root, long long recursiveSum, const int targetSum)
{//深度优先搜索dfs
if(!root)
{//空节点
return 0;
}
int path = 0;
recursiveSum += root->val;
if(targetSum == recursiveSum)
{//节点值可为负数,因此可以继续递归
path++;
}
//前序遍历
path += exhaustivePath(root->left, recursiveSum, targetSum);
path += exhaustivePath(root->right, recursiveSum, targetSum);
return path;
}
public:
/**
* 计算路径和外部调用接口
**/
int pathSum(shared_ptr<TreeNode> &root, const int targetSum, const int method)
{
if(METHOD_EXHAUSTIVITY == method)
{
return exhaustiveMethod(root, targetSum);
}
else if(METHOD_PREFIX == method)
{
preSum[0] = 1; //符合要求的以二叉树根节点为起始的路径
return prefixSumMethod(root, 0, targetSum);
}
return 0;
}
/**
* 根据输入序列构造二叉树
**/
void buildTree(shared_ptr<TreeNode> &root, const vector<int> &input)
{//使用BFS宽度/广度优先搜索算法,从上到下、同层从左至右构造每个节点
const unsigned short n = input.size();
if((!n)
|| (DUMMY_NULL == input[0])) //注意顺序
{
return;
}
queue<pair<unsigned short, shared_ptr<TreeNode>>> q; //key存放节点在原始输入序列中的索引位置
pair<unsigned short, shared_ptr<TreeNode>> tmp;
root = make_shared<TreeNode>(input[0]);
q.push(make_pair(0,root));
for(unsigned short i = 0; n > i; ++i) //每个节点均是根节点
{
const unsigned short size = q.size();
for(unsigned short j = 0; size > j; ++j)
{
tmp = q.front();
unsigned short pos = tmp.first + (tmp.first + 1); //left child node
if(n <= pos)
{//该父节点的左孩子节点超出输入序列范围,该父节点是叶子节点
i = n;
break;
}
if(DUMMY_NULL != input[pos])
{
tmp.second->left = make_shared<TreeNode>(input[pos]);
q.push(make_pair(pos, tmp.second->left));
}
pos = tmp.first + (tmp.first + 1) + 1; //right child node
if(n <= pos)
{//该父节点的右孩子节点超出输入序列范围(由于左孩子节点存在,所以该父节点不是叶子节点)
i = n;
break;
}
if(DUMMY_NULL != input[pos])
{
tmp.second->right = make_shared<TreeNode>(input[pos]);
q.push(make_pair(pos, tmp.second->right));
}
q.pop(); //这里虽弹出,但指针并不会释放,充分理解智能指针引用计数原理:每次 make_shared 和 push 计数器均加1,pop一次仅减1,所以最终各非空节点计数器数值均为1
}
}
return;
}
/**
* 从上到下打印二叉树的每个节点,同一层按从左至右的顺序,同一层不存在的节点输出null
* 设计思路是将二叉树同一层最多数量pow(2, level-1)的节点都插入到队列中,包括不存在的节点位置。
* 如果仅插入已存在的节点,下一次遍历时很难确定节点在二叉树同层的哪个位置,尤其是多层结构,需要向前追溯。
**/
void levelOrderPrint_Comm(shared_ptr<TreeNode> const &root)
{
unordered_map<short, short> unmap; //按先后顺序缓存各节点元素
queue<shared_ptr<TreeNode>> q; //缓存同一层节点指针(包括空节点)
shared_ptr<TreeNode> tmp;
short n = 0;
short lev = 0, inx = 0;
bool flag = false; //判断队列中缓存的同一层节点指针是否全是无效的空节点
if(nullptr == root)
{
cout << "null" << endl;
return;
}
q.push(root);
while(!flag)
{
flag = true;
++lev;
n = q.size();
for(short i = 0; n > i; ++i)
{
tmp = q.front();
if(nullptr == tmp)
{
// flag = true; //不能放此处,同层左边有,右边无
unmap[inx++] = __SHRT_MAX__;
q.pop();
// 下一层
q.push(nullptr);
q.push(nullptr);
continue;
}
else
{
flag = false;
unmap[inx++] = tmp->val;
}
q.pop(); //push 和 pop 各一次,作用于同一节点上的引用计数相互抵消
if(nullptr != tmp->left)
{
q.push(tmp->left);
}
else
{
q.push(nullptr);
}
if(nullptr != tmp->right)
{
q.push(tmp->right);
}
else
{
q.push(nullptr);
}
}
}
// 上面while循环多计一层,最后queue中存放的全是nullptr
--lev;
n = 0;
for(short exp = 0; lev > exp; ++exp)
{// 计算二叉树节点总数(可以由外部输入)
// 第一层(根节点),元素个数最多 pow(2,0) 个
// 第二层,元素个数最多 pow(2,1) 个
// 第三层,元素个数最多 pow(2,2) 个
// ……
// 第N层,元素个数最多 pow(2,(N-1)) 个
// n += pow(2,exp); //转 移位运算 或 等比数列求和公式 可提升效率
n += 1<<exp;
}
cout << unmap[0];
for(short i = 1; n > i; ++i)
{
if(__SHRT_MAX__ == unmap[i])
{
cout << ",null";
}
else
{
cout << ',' << unmap[i];
}
}
cout << endl;
return;
}
private:
unordered_map<long long, int> preSum; //将各递归和作为key,该和值出现的次数作为value
};
int main(void)
{
const unordered_multimap<int,vector<int>> input = { {8,{10,5,-3,3,2,DUMMY_NULL,11,3,-2,DUMMY_NULL,1}},
{22,{5,4,8,11,DUMMY_NULL,13,4,7,2,DUMMY_NULL,DUMMY_NULL,5,1}},
{8,{6,3,4,7,-1,3,7,8,1,DUMMY_NULL,2,DUMMY_NULL,DUMMY_NULL,2,-3,DUMMY_NULL,DUMMY_NULL,DUMMY_NULL,DUMMY_NULL,DUMMY_NULL,DUMMY_NULL,DUMMY_NULL,4}},
{8,{8}},
{8,{12}},
{8,{}} };
Solution sl;
shared_ptr<TreeNode> root = nullptr;
for(const auto i : input)
{
cout << i.first << ", num=" << i.second.size() << endl;
sl.buildTree(root, i.second);
sl.levelOrderPrint_Comm(root);
cout << "prePathSum=" << sl.pathSum(root, i.first, METHOD_PREFIX) << ", exhaustPathSum=" << sl.pathSum(root, i.first, METHOD_EXHAUSTIVITY) << endl;
cout << endl;
root = nullptr;
}
return 0;
}
郑重提示:①解题思路非最优,覆盖条件可能不全,仅供练习参考。
②若有更佳思路或疑问,可在评论区留言相互讨论,不亦乐乎。
③本文不允许转载,若认可本文,可点赞收藏关注。
最后
以上就是爱听歌大船最近收集整理的关于数据结构和算法:二叉树路径总和的全部内容,更多相关数据结构和算法内容请搜索靠谱客的其他文章。








发表评论 取消回复