先看实例,沾沾自喜得意洋洋的时候。
自己在测试过程中遇到个坑,这点需要注意。
在处理游戏战斗过程中解决服务器端与客户端同步问题的帖子
【小伟哥游戏之路】游戏中战斗回放与离线回放的实现机制总结
写完后,自己有所担心是否有遗漏的地方。哪里肯定会出问题,不能迷惑大家和以后的自己。
先看实例 Java实现过程
package yangww;
import java.util.Random;
public class RandomTest {
public static void main(String[] args) {
// java.util.Random 随机化的种子(seed) 的使用
long seed = 123456;
System.out.println("测试随机种子数据");
Random random = new Random(seed);
for (int i = 0; i < 10; i++) {
System.out.print(random.nextInt(100) + " ");
}
System.out.println("nn重新根据seed进行随机");
Random randomNew = new Random(seed);
for (int i = 0; i < 10; i++) {
System.out.print(randomNew.nextInt(100) + " ");
}
}
}输出结果
测试随机种子数据
23 47 67 85 38 83 97 96 4 7
重新根据seed进行随机
23 47 67 85 38 83 97 96 4 7 再看python2.7环境实现过程
import random
random.seed(123456)
for i in range(1, 10):
print(random.randint(1, 100))
输出结果
81 80 3 18 1 67 8 27 12
搞毛线,如果这样,服务器与客户端怎么进行同步,随机数序列完全不同。
不同开发语言产生的随机数序列又不相同,因此当结果出现差异时,很难分辨出是由于程序算法方面的原因造成的,还是由于随机数序列的不同造成的。
查资料后发现 python 中的numpy源码random模块实现方式和java的 不同。
经查阅numpy文档,可知numpy生成随机数采用的是MersenneTwister算法,这是随机数生成的经典方法,来自于1998年ACM Transactions on Modeling and Computer Simulation中的一篇论文,在维基上有详细介绍(https://en.wikipedia.org/wiki/Mersenne_Twister),论文也可在此处下载。其基本思路是,根据给定的随机数种子,先通过一系列运算,生成624个整数key;再以这624个key为基础,生成一系列满足均匀分布的、在0到2^32-1之间的伪随机整数。其他程序可以对这些伪随机整数进行再加工,生成符合其他概率分布形态的随机数。
经阅读numpy源码,其生成随机数的核心程序为numpy/random/mtrand目录下的randomkit.c,其中几个主要的函数如下:
1、rk_seed(unsigned long seed, rk_state *state):基于Mersenne Twister算法,初始化624个整数key,放在state结构体中。
2、rk_random(rk_state *state):基于Mersenne Twister算法,生成一个32位的、服从均匀分布的随机数。
3、rk_double(rk_state *state):生成一个0到1之间的、服从均匀分布的随机数。基本原理是:首先调用rk_random()函数生成两个32个随机数a、b,然后将a右移5位、保留27位,将b右移6位、保留26位,再将a、b按位串接在一起,形成一个53位的整数,再除以2^53。源代码如下:
long a = rk_random(state)>> 5, b = rk_random(state) >> 6;
return (a * 67108864.0 +b) / 9007199254740992.0;4、rk_gauss(rk_state*state):生成一个服从正态分布N(0, 1)的随机数。这一部分numpy利用了Box–Muller变换公式,它是一种将均匀分布转换成正态分布的经典方法,在维基上有详细介绍(https://en.wikipedia.org/wiki/Box%E2%80%93Muller_transform)。Box-Muller变换有基本公式和极坐标公式两种形态,numpy采用的是极坐标公式,即:假设u, v是两个服从均匀分布的、0到1之间的随机数,则以下z0、z1服从正态分布N(0, 1):
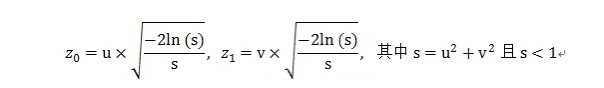
源代码如下:
do {
x1 = 2.0*rk_double(state) - 1.0;
x2 = 2.0*rk_double(state) - 1.0;
r2 = x1*x1 + x2*x2;
} while (r2 >= 1.0 || r2 == 0.0);
f = sqrt(-2.0*log(r2)/r2);
state->gauss = f*x1;
return f*x2;
三、Java apache math3源代码分析
经搜索,java社区的apache math3已经提供了一个Mersenne Twister算法的开源实现,于是下载源代码分析了一下。Apache math3的Mersenne Twister算法实现类为org.apache.commons.math3.random.MersenneTwister,其中主要方法有:
1、setSeed(intseed):初始化624个整数key;
2、next(intbits),生成不超过32位的伪随机整数。
经阅读源码,发现上述算法的具体实现虽然与numpy的C语言版本略有差异,但结果应该是一致的。经测试验证,果然如此,在给定相同seed情况下,两者生成的32位随机整数序列是相同的。
因此,numpy和math3随机数序列的差异,主要是由于对Mersenne Twister算法结果的后续加工处理方法不同。Apache math3生成其他形态随机数的方法在MersenneTwister的父类BitsStreamGenerator中定义,其中主要方法有:
1、nextDouble():生成一个0到1之间的、服从均匀分布的随机数。基本原理是:首先调用MersenneTwister的next()函数生成两个26位的随机整数a、b,再将a、b按位串接在一起,形成一个52位的整数,再除以2^52。源代码如下:
final long high = ((long) next(26))<< 26;
final int low =next(26);
return (high | low) * 0x1.0p-52d;由此可见,math3和numpy的差异在于,math3使用的是52位随机数,而numpy使用的是53位随机数。
2、nextGaussian():生成一个服从正态分布N(0,1)的随机数。这一部分math3也是利用了Box–Muller变换公式,但是与numpy不同的是,它没有采用Box–Muller极坐标公式,而是使用Box–Muller基本公式,即:假设x, y是两个服从均匀分布的、0到1之间的随机数,则以下z0、z1服从正态分布N(0, 1):

源代码如下:
final double x = nextDouble();
final double y = nextDouble();
final double alpha = 2 *FastMath.PI * x;
final double r = FastMath.sqrt(-2 * FastMath.log(y));
random = r * FastMath.cos(alpha);
nextGaussian = r * FastMath.sin(alpha);
四、解决方案
基于以上分析,我们可以在自己的Java代码中继承MersenneTwister类,覆盖其中的nextDouble、nextGaussian等方法,将其改为与numpy一致的算法即可。源代码如下:
public class NumpyRandom extends MersenneTwister {
private boolean has_gauss = false;
private double gauss = 0;
public double nextDouble() {
int a = next(32) >>> 5;
int b = next(32) >>> 6;
return (a * 67108864.0 + b) / 9007199254740992.0;
}
public double nextGaussian() {
if (has_gauss) {
double tmp = gauss;
gauss = 0;
has_gauss = false;
return tmp;
} else {
double x1, x2, s;
do {
x1 = 2.0 * nextDouble() - 1.0;
x2 = 2.0 * nextDouble() - 1.0;
s = x1 * x1 + x2 * x2;
} while (s >= 1.0 || s == 0.0);
double f = Math.sqrt(-2.0 * Math.log(s) / s);
gauss = f * x1;
has_gauss = true;
return f * x2;
}
}
public static void main(String[] args) {
NumpyRandom rand = new NumpyRandom();
rand.setSeed(1000);
for (int i = 0; i < 10; i++)
System.out.println(" " + rand.nextGaussian());
}
}经测试,上述程序产生的正态分布随机数与python numpy的结果完全相同。
最后
以上就是暴躁雪碧最近收集整理的关于【小伟哥游戏之路】Java与Python实现seed()随机数序列同步问题的解决方案的全部内容,更多相关【小伟哥游戏之路】Java与Python实现seed()随机数序列同步问题内容请搜索靠谱客的其他文章。








发表评论 取消回复