旋转图像48-力扣（二维数组+py3）

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1：

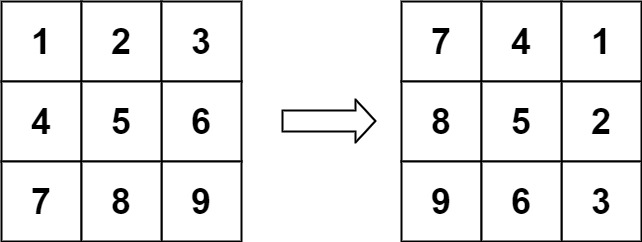
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

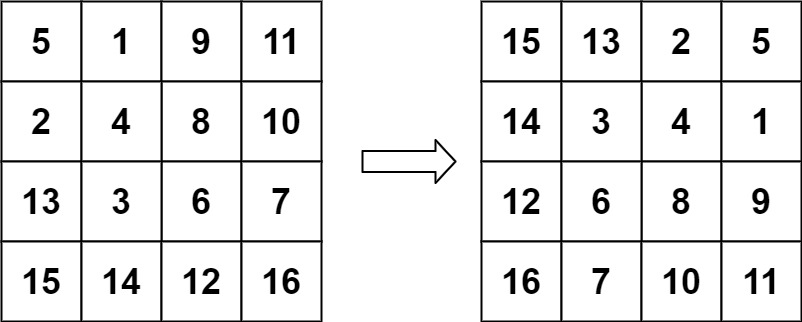
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

示例 3：

输入：matrix = [[1]]
输出：[[1]]
示例 4：

输入：matrix = [[1,2],[3,4]]
输出：[[3,1],[4,2]]

提示：

matrix.length == n
matrix[i].length == n
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/rotate-image
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

对于矩阵中第 i 行的第 j 个元素，在旋转后，它出现在倒数第 i 列的第 j 个位置。我们将其翻译成代码。由于矩阵中的行列从 0开始计数，因此对于矩阵中的元素 $\text{matrix}[\text{row}][\text{col}]$，在旋转后，它的新位置为 ${\text{matrix}}_{\text{new}}[\text{col}][n-\text{row}-1]$。（对于矩阵转置会有$[row][col]$变$[col][row]$，对于这里的旋转矩阵相对于矩阵转置而言，可以看作先转置，然后右移，所以列变行即 col 变 row 这个规律不改变，行变列即row变col这个规律需要改变，即向右平移两列总结为n - row - 1）其中n为矩阵的行数.

然后我们使用一个与 $\text{matrix}$大小相同的辅助数组 ${matrix}_{\text{new}}$ ，临时存储旋转后的结果。我们遍历 $\text{matrix}$ 中的每一个元素，根据上述规则将该元素存放到 ${matrix}_{\text{new}}$ 中对应的位置。在遍历完成之后再将${matrix}_{\text{new}}$ 中的结果复制到原数组中即可.

但是对于原地修改而言，会存在什么问题呢，如果我们直接将 matrix[row][col] 放到原矩阵中的目标位置 matrix[col][n−row−1]，matrix[col][n−row−1]会被覆盖掉，因此我们可以考虑用一个临时变量 temp 暂存matrix[col][n−row−1]的值。而matrix[col][n−row−1]旋转后会到到什么位置呢，因为由公式：matrix[row][col] 到 matrixnew [col][n−row−1]（我们最开始得出的规律）

将row=col，col=n-row-1可得：
matrix[col][n-row-1] 到 matrixnew[n-row-1][n-col-1]，
matrix[n-row-1][n-col-1]旋转会到什么位置，我们再重复上述步骤可以得到
matrix[n-row-1][n-col-1]到matrixnew[n-col-1][row],
matrix[n-col-1][row]会到什么位置呢，重复上述计算步骤，代入可得
matrix[n-col-1][row]到marixnew[row][col]回到了起点。一圈相当于已经旋转结束

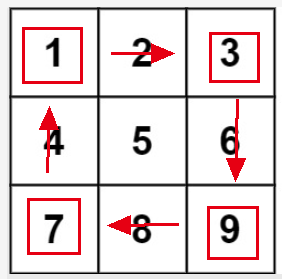
因此一个旋转循环有：

matrix[row][clo] 到 matrix[col][n−row−1]
matrix[col][n-row-1] 到 matrixnew[n-row-1][n-col-1]，
matrix[n-row-1][n-col-1]到matrixnew[n-col-1][row],
matrix[n-col-1][row]到marixnew[row][col]，

用代码可以表示为（例如：保存一圈中最后一个要旋转的变量记录到临时变量，然后旋转，最后一次旋转时，注意：该位置的元素已被覆盖，因此此时利用临时变量赋给第一个旋转的元素即可。）
temp = matrix[n-col-1][row]
matrix[col][n−row−1] = matrix[row][clo]
matrix[n-row-1][n-col-1] = matrix[col][n-row-1]
matrix[n-col-1][row] = matrix[n-row-1][n-col-1]
matrix[row][clo] = temp

这里还有一个问题没有解决：我们应该枚举哪些位置 (row,col) 进行上述的原地交换操作？由于每一次原地交换四个位置，因此
当 n 为偶数时，我们需要枚举 $n^2/4=(n/2)\times (n/2)$ 个位置，可以将该图形分为四块，以 $4\times 4$ 的矩阵为例

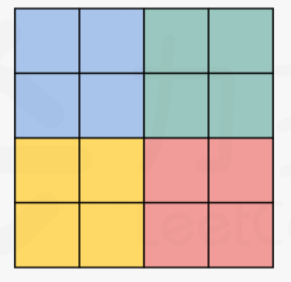
保证了不重复、不遗漏；
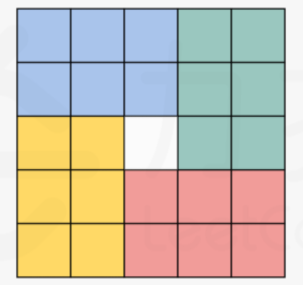
当 n 为奇数时，由于中心的位置经过旋转后位置不变，我们需要枚举$(n^2-1)/4=((n-1)/2)\times ((n+1)/2)$个位置，需要换一种划分的方式，以 $5\times 5$的矩阵为例：

python实现的源码：

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        for i in range(n // 2):
            for j in range((n + 1) // 2):
                matrix[i][j], matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1] 
                    = matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1], matrix[i][j]

做这种题如果沉不住气，肯定很难做出来，一定得有耐心。

参考：
链接：https://leetcode-cn.com/problems/rotate-image

最后

以上就是慈祥蜡烛为你收集整理的旋转图像48-力扣（二维数组+py3）的全部内容，希望文章能够帮你解决旋转图像48-力扣（二维数组+py3）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。