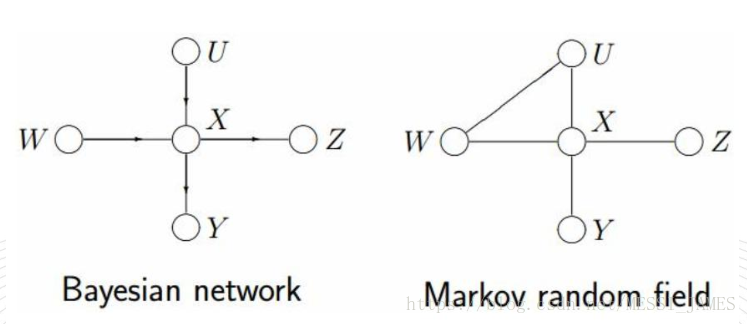
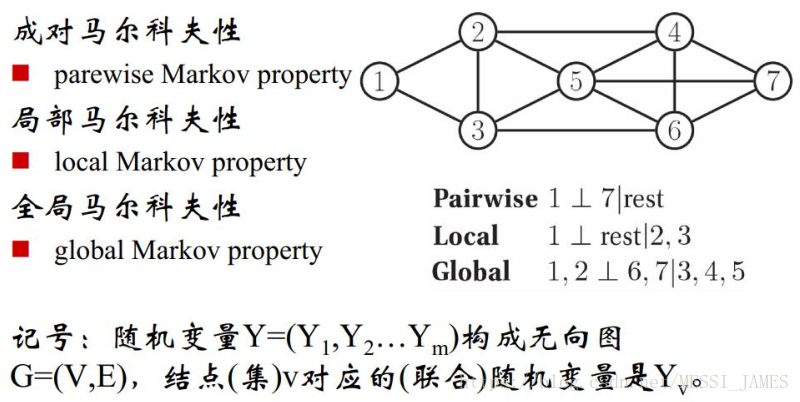
1.X8的马尔科夫毯
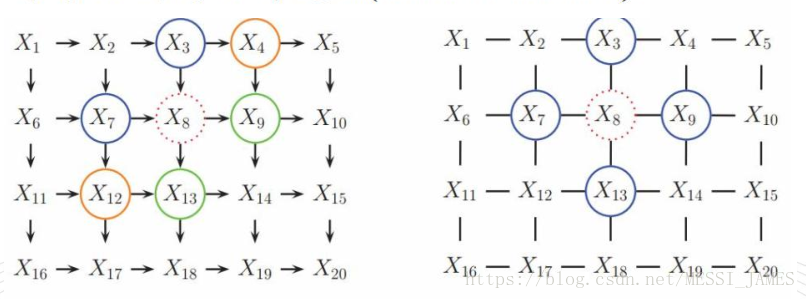
!
(1)有向图转换成无向图(UGM)
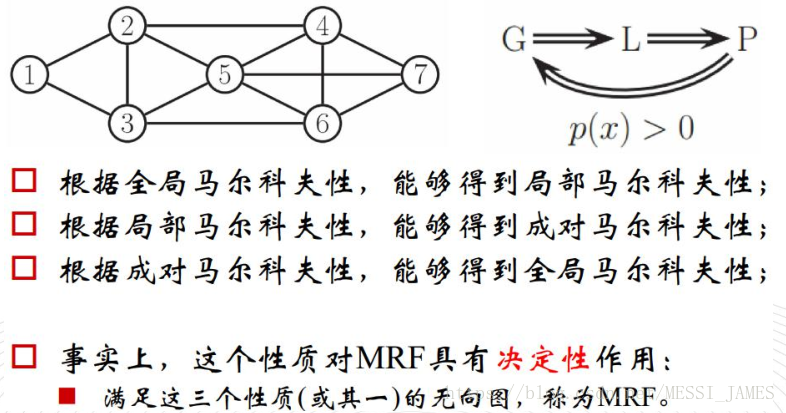
(2)马尔科夫
三个性质等价
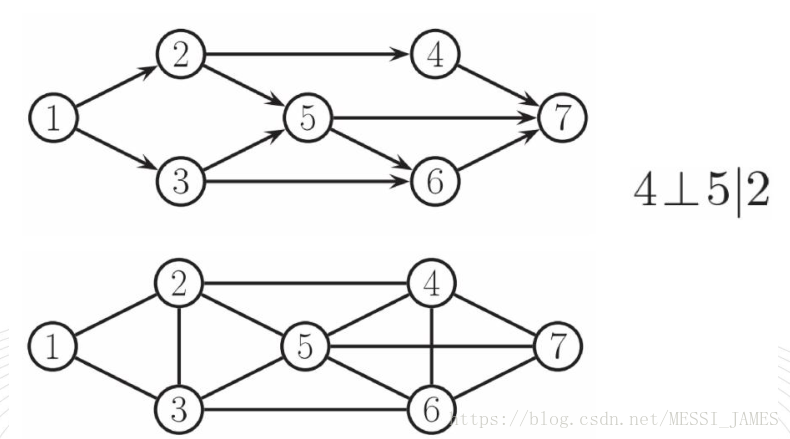
(3)团和最大团
深度学习中的激活函数导引
参考https://zhuanlan.zhihu.com/p/22142013
1激活函数的定义与作用
(1)定义
在人工神经网络中,神经元节点的激活函数定义了对神经元输出的映射。
简单来说,神经元的输出(例如,全连接网络中就是输入向量与权重向量的内积再加上偏置项)经过激活函数处理后再作为输出。
(2)作用
神经网络中激活函数的主要作用是
提供网络的非线性建模能力,激活函数一般是非线性函数。
假设一个示例神经网络中仅包含线性卷积和全连接运算,那么该网络仅能够表达线性映射,即便增加网络的深度也依旧还是线性映射,难以有效建模实际环境中非线性分布的数据。加入(非线性)激活函数之后,深度神经网络才具备了分层的非线性映射学习能力。因此,激活函数是深度神经网络中不可或缺的部分。
2.几种激活函数
从定义来看,几乎所有的连续可导函数都可以用作激活函数。但目前常见的多是分段线性和具有指数形状的非线性函数。(1)Sigmoid
sigmoid 在定义域内处处可导,且两侧导数逐渐趋近于0
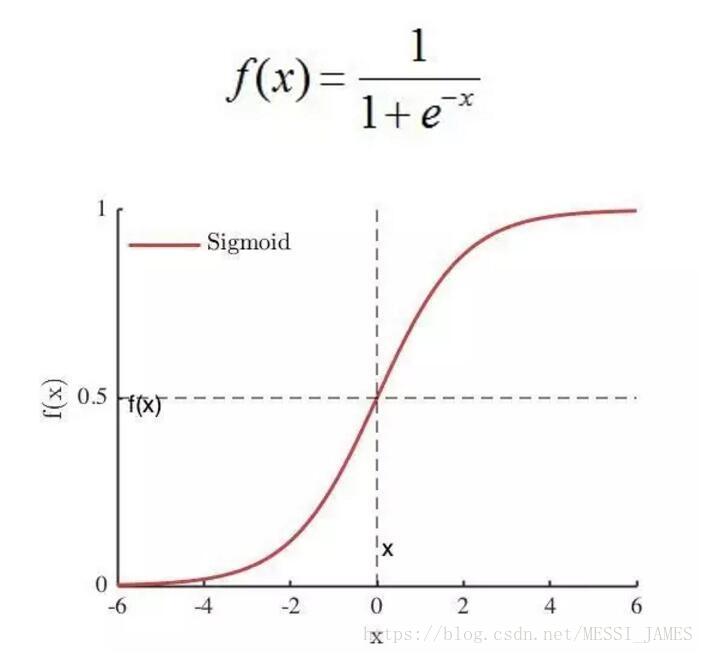
软饱和激活函数
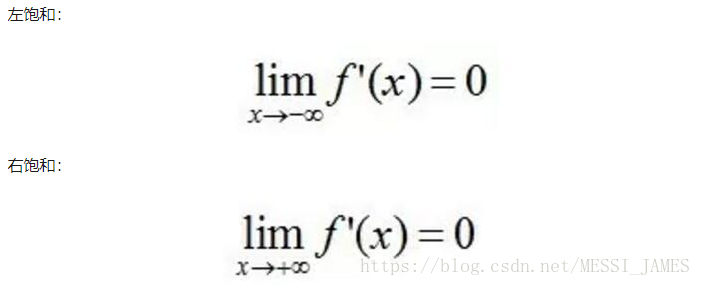
硬饱和激活函数
f’(x)=0,当 |x| > c,其中 c 为常数。
…
Sigmoid 的软饱和性,使得深度神经网络在二三十年里一直难以有效的训练,是阻碍神经网络发展的重要原因。具体来说,由于在后向传递过程中,sigmoid向下传导的梯度包含了一个f’(x) 因子(sigmoid关于输入的导数),因此一旦输入落入饱和区,f’(x) 就会变得接近于0,导致了向底层传递的梯度也变得非常小。此时,网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说, sigmoid 网络在 5 层之内就会产生梯度消失现象[2]。梯度消失问题至今仍然存在,但被新的优化方法有效缓解了,例如DBN中的分层预训练,Batch Normalization的逐层归一化,Xavier和MSRA权重初始化等代表性技术。
需要尤其注意参数的初始值来尽量避免饱和的情况。如果你的初始值很大的话,大部分神经元可能都会处在saturation的状态而把gradient kill掉,这会导致网络变的很难学习。
Sigmoid 的饱和性虽然会导致梯度消失,但也有其有利的一面。例如它在物理意义上最为接近生物神经元。 (0, 1) 的输出还可以被表示作概率,或用于输入的归一化,代表性的如Sigmoid交叉熵损失函数。
(2)tanh
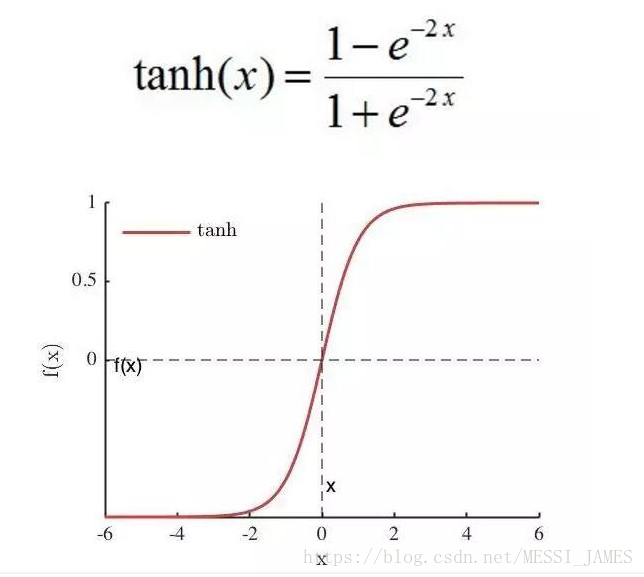
tanh(x)=2sigmoid(2x)-1,也具有软饱和性。
tanh 网络的收敛速度要比sigmoid快。因为tanh 的输出均值比 sigmoid 更接近 0,SGD会更接近 natural gradient[4](一种二次优化技术),从而降低所需的迭代次数。
(3)ReLU
深度网络的直接监督式训练的最终突破,最主要的原因是采用了新型激活函数ReLU[5, 6]。与传统的sigmoid激活函数相比,
ReLU能够有效缓解梯度消失问题,从而直接以监督的方式训练深度神经网络,无需依赖无监督的逐层预训练,这也是2012年深度卷积神经网络在ILSVRC竞赛中取得里程碑式突破的重要原因之一。
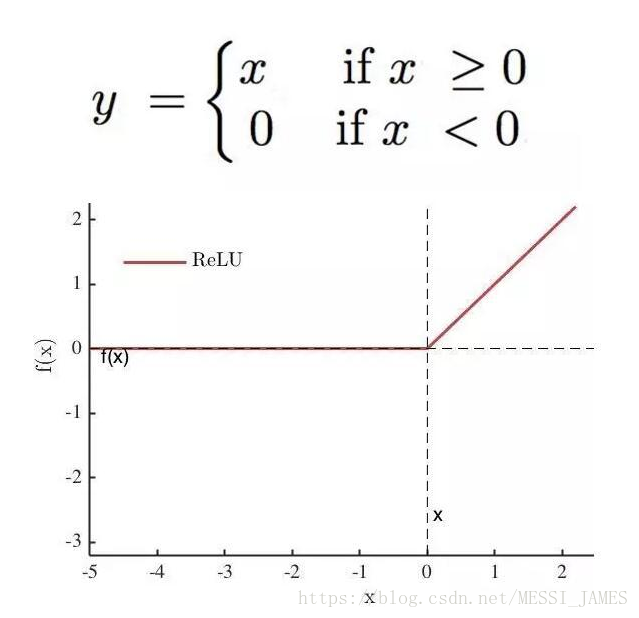
一个非常大的梯度流过一个 ReLU 神经元,更新过参数之后,这个神经元再也不会对任何数据有激活现象了。
(4)Leaky ReLU
Leaky Relu是用来解决ReLU中dead神经元问题的。
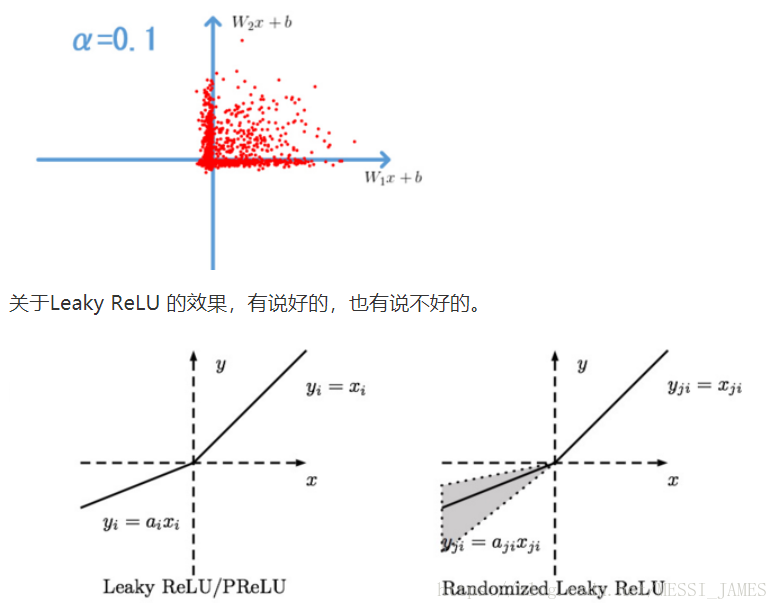
Parametric ReLU: 对于 Leaky ReLU 中的,通常都是通过先验知识人工赋值的。 然而可以观察到,损失函数对的导数我们是可以求得的,可不可以将它作为一个参数进行训练呢? Kaiming He的论文《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》指出,不仅可以训练,而且效果更好。
原文说使用了Parametric ReLU后,最终效果比不用提高了1.03%.
Randomized ReLU: Randomized Leaky ReLU 是 leaky ReLU 的random 版本 ( 是random的)。在训练过程中,是从一个高斯分布 中 随机出来的,然后在测试过程中进行修正。
(5)Momentum

γ是空气阻力
最后
以上就是乐观唇膏最近收集整理的关于马尔科夫、条件随机场、激活函数1.X8的马尔科夫毯深度学习中的激活函数导引的全部内容,更多相关马尔科夫、条件随机场、激活函数1.X8内容请搜索靠谱客的其他文章。










发表评论 取消回复