UTF8gbsn
傅里叶级数和傅里叶变换都是十分重要的数学工具.但是学习起来也有一定的难度.写本文的目的是想以一种更为直观的角度来理解这种变换.我们采用的观点是来自于线性代数的.所以我们有必要从线性代数开始.
基本定义
在线性代数中,有一个非常重要的概念叫做正交.比如
(
1
,
0
,
0
)
(1,0,0)
(1,0,0)与
(
0
,
1
,
0
)
(0,1,0)
(0,1,0)就是互相正交的向量.而正交向量的点积为0.也就是说
(
1
,
0
,
0
)
⋅
(
0
,
1
,
0
)
=
0
(1,0,0)cdot (0,1,0)=0
(1,0,0)⋅(0,1,0)=0.
我们可以看到正交的概念十分简单明了.但是实际上正交的概念更为普遍,不只是线性代数中才有的概念.更为抽象的定义是如果你定义某种操作函数K,如果
K
(
a
,
b
)
=
0
K(a,b)=0
K(a,b)=0,我们就可以称为a,b正交.所以我们可以在三角函数中定义正交的概念.
三角函数中的正交
这里我们先列出来正交的三角函数有 1 , c o s ( x ) , s i n ( x ) , c o s ( 2 x ) , s i n ( 2 x ) , ⋯ , c o s ( n x ) , s i n ( n x ) , ⋯ 1, cos(x), sin(x), cos(2x), sin(2x),cdots, cos(nx), sin(nx), cdots 1,cos(x),sin(x),cos(2x),sin(2x),⋯,cos(nx),sin(nx),⋯.这些函数在 [ − π , π ] [-pi, pi] [−π,π]上正交.也就是说,
∫
−
π
π
c
o
s
(
n
x
)
d
x
=
0
int_{-pi}^{pi}{cos(nx)dx}=0
∫−ππcos(nx)dx=0
∫
−
π
π
s
i
n
(
n
x
)
d
x
=
0
int_{-pi}^{pi}{sin(nx)dx}=0
∫−ππsin(nx)dx=0
∫
−
π
π
s
i
n
(
k
x
)
c
o
s
(
n
x
)
d
x
=
0
int_{-pi}^{pi}{sin(kx)cos(nx)dx}=0
∫−ππsin(kx)cos(nx)dx=0
∫
−
π
π
s
i
n
(
k
x
)
s
i
n
(
n
x
)
d
x
=
0
,
(
k
≠
n
)
int_{-pi}^{pi}{sin(kx)sin(nx)dx}=0,(kneq n)
∫−ππsin(kx)sin(nx)dx=0,(k=n)
∫
−
π
π
c
o
s
(
k
x
)
c
o
s
(
n
x
)
d
x
=
0
,
(
k
≠
n
)
int_{-pi}^{pi}{cos(kx)cos(nx)dx}=0,(kneq n)
∫−ππcos(kx)cos(nx)dx=0,(k=n)
我们来看看类比,对于向量
a
=
(
a
1
a
2
⋯
a
n
)
,
b
=
(
b
1
b
2
⋯
b
n
)
mathbf{a}=left( begin{array}{cccc} a_1 & a_2 & cdots & a_n end{array} right),mathbf{b}=left( begin{array}{cccc} b_1 & b_2 & cdots & b_n end{array} right)
a=(a1a2⋯an),b=(b1b2⋯bn)我们定义的K操作为
K
(
a
,
b
)
=
a
1
b
1
+
a
2
b
2
+
⋯
+
a
n
b
n
K(a,b)=a_1b_1+a_2b_2+cdots+a_nb_n
K(a,b)=a1b1+a2b2+⋯+anbn.那么对于三角函数而言,K操作定义为
K
(
c
o
s
(
k
x
)
,
s
i
n
(
n
x
)
)
=
∫
−
π
π
c
o
s
(
k
x
)
s
i
n
(
n
x
)
d
x
K(cos(kx),sin(nx))=int_{-pi}^{pi}{cos(kx)sin(nx)dx}
K(cos(kx),sin(nx))=∫−ππcos(kx)sin(nx)dx
所以我们可以对于三角函数建立正交关系.我们来类比一下.
向量空间 vs 三角函数的正交空间
-
基向量
-
向量空间中(假如这个空间的维度为n),我们把这个空间称为A
我们可以定义基向量为 e 1 = ( 1 , 0 , ⋯ , 0 ) e_1=(1,0,cdots,0) e1=(1,0,⋯,0)
e 2 = ( 0 , 1 , ⋯ , 0 ) e_2=(0,1,cdots,0) e2=(0,1,⋯,0) ⋮ vdots ⋮ e n = ( 0 , 0 , ⋯ , 1 ) e_n=(0,0,cdots,1) en=(0,0,⋯,1) -
对于三角函数的空间里面我们可以定义的一组基为,我们也把这个空间称为B
n 1 = 1 n_1=1 n1=1 n 2 = c o s ( x ) n_2=cos(x) n2=cos(x) n 3 = c o s ( 2 x ) n_3=cos(2x) n3=cos(2x) ⋮ vdots ⋮
n n = c o s ( ( n − 1 ) x ) n_n=cos((n-1)x) nn=cos((n−1)x) 由这些基组成的空间,它是一个n维的三角函数空间
-
-
空间中任意一个向量
-
n维向量空间A v = k 1 e 1 + k 2 e 2 + ⋯ + k n e n v=k_1e_1+k_2e_2+cdots+k_ne_n v=k1e1+k2e2+⋯+knen
-
刚才提到的三角函数空间B f = k 0 1 + k 1 c 1 + ⋯ + k n − 1 c n − 1 f=k_01+k_1c_1+cdots+k_{n-1}c_{n-1} f=k01+k1c1+⋯+kn−1cn−1
f = k 0 + k 1 c o s ( x ) + k 2 c o s ( 2 x ) + ⋯ + k n − 1 c o s ( ( n − 1 ) x ) f=k_0+k_1cos(x)+k_2cos(2x)+cdots+k_{n-1}cos((n-1)x) f=k0+k1cos(x)+k2cos(2x)+⋯+kn−1cos((n−1)x)
-
如何求系数
-
向量空间中如何求坐标.也就是基向量的系数.比如
v = k 1 e 1 + k 2 e 2 + ⋯ + k n e n v=k_1e_1+k_2e_2+cdots+k_ne_n v=k1e1+k2e2+⋯+knen
这个向量的系数(坐标)是多少呢?通过上式你可以很容易观察得到坐标为 ( k 1 , k 2 , ⋯ , k n ) left( k_1, k_2, cdots, k_n right) (k1,k2,⋯,kn).但是实际生活中,你并不知道上面的形式,你知道 v v v而不知道 v v v怎么由 ( e 1 , e 2 , ⋯ , e n ) left( e_1, e_2, cdots, e_n right) (e1,e2,⋯,en)构成的.我们的问题变成,已知 v v v,和 ( e 1 , e 2 , ⋯ , e n ) left( e_1, e_2, cdots, e_n right) (e1,e2,⋯,en),求 v v v在 ( e 1 , e 2 , ⋯ , e n ) left( e_1, e_2, cdots, e_n right) (e1,e2,⋯,en)这组基下面的坐标.在线性代数中,这个问题其实很简单.我们只需要用 e i e_i ei去点积 v v v即可.
k i = v ⋅ e i k_i=vcdot e_i ki=v⋅ei
这样就可以求出在 ( e 1 , e 2 , ⋯ , e n ) left( e_1, e_2, cdots, e_n right) (e1,e2,⋯,en)下, v v v的坐标.因为 e i ⋅ e j = 0 , ( i ≠ j ) e_icdot e_j=0,(ineq j) ei⋅ej=0,(i=j)
-
三角函数空间
类似的我们如果已知函数 f ( x ) f(x) f(x)由如下的三角函数组成
1 , c o s ( x ) , s i n ( x ) , c o s ( 2 x ) , s i n ( 2 x ) , ⋯ , c o s ( n x ) , s i n ( n x ) 1, cos(x),sin(x),cos(2x),sin(2x),cdots,cos(nx),sin(nx) 1,cos(x),sin(x),cos(2x),sin(2x),⋯,cos(nx),sin(nx)但是你不知道 f ( x ) f(x) f(x)对应这些三角函数的具体系数.你该如何做?类似于向量空间的方法,使用三角函数中定义的点积来求出对应系数 k i k_i ki
比如我们要来求出 c o s ( i x ) cos(ix) cos(ix)的系数,我们可以使用
∫ − π π f ( x ) c o s ( i x ) d x = k i ( c o s ) ∫ − π π c o s ( i x ) c o s ( i x ) d x int_{-pi}^{pi}f(x)cos(ix)dx=k_i^{(cos)}int_{-pi}^{pi}{cos(ix)cos(ix)dx} ∫−ππf(x)cos(ix)dx=ki(cos)∫−ππcos(ix)cos(ix)dx这是应为正交的关系,所以只剩下一项了.又因为我们知道
∫ − π π c o s 2 ( i x ) d x = ∫ − π π c o s ( 2 i x ) + 1 2 d x = ∫ − π π c o s ( 2 i x ) 2 d x + 1 2 ∫ − π π d x = π int_{-pi}^{pi}{cos^2(ix)dx}=int_{-pi}^{pi}{frac{cos(2ix)+1}{2}dx}=int_{-pi}^{pi}{frac{cos(2ix)}{2}dx}+frac{1}{2} int_{-pi}^{pi}{dx}=pi ∫−ππcos2(ix)dx=∫−ππ2cos(2ix)+1dx=∫−ππ2cos(2ix)dx+21∫−ππdx=π
由此可见 k i c o s = ∫ − π π f ( x ) c o s ( i x ) d x / π k_i^{cos}=int_{-pi}^{pi}{f(x)cos(ix)dx}/pi kicos=∫−ππf(x)cos(ix)dx/π
傅里叶级数
有了前面的知识,我们自然而然的就可以导出傅里叶级数了.我们先来看看傅里叶级数的定义.
如果 f ( x ) f(x) f(x)是周期 2 π 2pi 2π的函数.那么以下展开形式被称作傅里叶级数
f ( x ) = a 0 2 + ∑ k = 1 ∞ ( a k c o s ( k x ) + b k s i n ( k x ) ) f(x)=frac{a_0}{2}+sum_{k=1}^{infty}(a_kcos(kx)+b_ksin(kx)) f(x)=2a0+k=1∑∞(akcos(kx)+bksin(kx))
其中,
a
0
=
1
π
∫
−
π
π
f
(
x
)
d
x
a_0=frac{1}{pi}int_{-pi}^{pi}{f(x)dx}
a0=π1∫−ππf(x)dx
b
k
=
1
π
∫
−
π
π
f
(
x
)
s
i
n
(
k
x
)
d
x
b_k=frac{1}{pi}int_{-pi}^{pi}{f(x)sin(kx)dx}
bk=π1∫−ππf(x)sin(kx)dx
a
k
=
1
π
∫
−
π
π
f
(
x
)
c
o
s
(
k
x
)
d
x
a_k=frac{1}{pi}int_{-pi}^{pi}{f(x)cos(kx)dx}
ak=π1∫−ππf(x)cos(kx)dx
有了傅里叶级数的定义,我们来看看收敛定理.
设 f ( x ) f(x) f(x)是周期为 2 π 2pi 2π的周期函数,如果它满足:
-
在一个周期内连续或只有有限个第一类间断点.
-
在一个周期内至多只有有限个极值点
则 f ( x ) f(x) f(x)的傅里叶级数收敛,且
-
当x是 f ( x ) f(x) f(x)的连续点时,级数收敛于 f ( x ) f(x) f(x).
-
当x是 f ( x ) f(x) f(x)的间断点时,级数收敛于 1 2 [ f ( x − ) + f ( x + ) ] frac{1}{2}[f(x^{-})+f(x^{+})] 21[f(x−)+f(x+)]
举例
傅里叶级数使用的互相正交的三角函数个数为无线个.也就是说这个三角函数空间为无线维的.但是我们可以在有限维度来观察福利叶级数的行为.我先来看看一个简单的例子比如函数,一个简单的连续函数.这个函数是周期为 2 π 2pi 2π的函数,这个函数的在 [ − π , π ] [-pi, pi] [−π,π]上面的定义为
{ x + π , ( − π < x ⩽ 0 ) − x + π , ( 0 < x ⩽ π ) left{ begin{aligned} x+pi, (-pi<xleqslant 0)\ -x+pi, (0<xleqslant pi) end{aligned} right. {x+π,(−π<x⩽0)−x+π,(0<x⩽π)
整个函数的图像如下图
我们这里不使用无线维的三角函数集合.而是使用有限维度的三角函数集合.会发生什么?比如我们使用
1 , c o s ( x ) , s i n ( x ) 1, cos(x),sin(x) 1,cos(x),sin(x)
按照我们刚开始的方法,也就是正交三角函数的系数求解方法.我们可以展开出这样的的形式
4
cos
(
x
)
π
+
π
2
frac{4 cos (x)}{pi }+frac{pi }{2}
π4cos(x)+2π
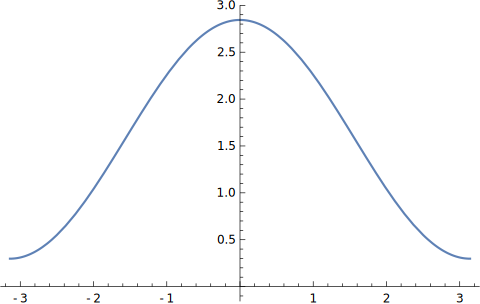
这个函数在
[
−
π
,
π
]
[-pi,pi]
[−π,π]的图象为.这个图象看起来和我们原来的函数图象比较起来,一点儿也不像.但是通过我们以前的分析,可以知道我们的原函数实际上,是含有
4
cos
(
x
)
π
frac{4 cos (x)}{pi }
π4cos(x)和
π
2
frac{pi }{2}
2π,成分的.但是因为我们并没有把更为高频的成分加入进来.
这个图形只能说大体上和我们原函数相像而已.接下来我们试着加入更高频的成分.
newpage
我们现在加入更高频的成分.
1 , c o s ( x ) , s i n ( x ) , c o s ( 2 x ) , s i n ( 2 x ) , c o s ( 3 x ) , s i n ( 3 x ) 1, cos(x), sin(x), cos(2x), sin(2x), cos(3x),sin(3x) 1,cos(x),sin(x),cos(2x),sin(2x),cos(3x),sin(3x)
我们求得的函数为
4 cos ( x ) π + 4 cos ( 3 x ) 9 π + π 2 frac{4 cos (x)}{pi }+frac{4 cos (3 x)}{9 pi }+frac{pi }{2} π4cos(x)+9π4cos(3x)+2π
图象为
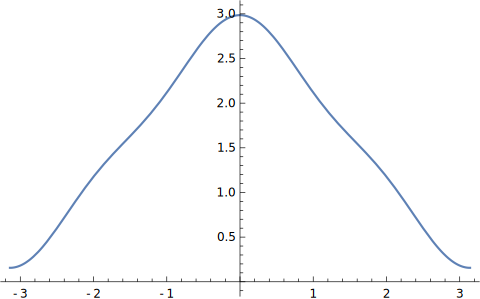
人眼可以看出,这个函数与原函数越来越像了.接下来我们加入更为高频的成分.比如
1
,
s
i
n
(
x
)
,
c
o
s
(
x
)
,
⋯
,
s
i
n
(
9
x
)
,
c
o
s
(
9
x
)
1,sin(x),cos(x),cdots, sin(9x),cos(9x)
1,sin(x),cos(x),⋯,sin(9x),cos(9x)
我们求得的函数为
4
cos
(
x
)
π
+
4
cos
(
3
x
)
9
π
+
4
cos
(
5
x
)
25
π
+
4
cos
(
7
x
)
49
π
+
4
cos
(
9
x
)
81
π
+
π
2
frac{4 cos (x)}{pi }+frac{4 cos (3 x)}{9 pi }+frac{4 cos (5 x)}{25 pi }+frac{4 cos (7 x)}{49 pi }+frac{4 cos (9 x)}{81 pi }+frac{pi }{2}
π4cos(x)+9π4cos(3x)+25π4cos(5x)+49π4cos(7x)+81π4cos(9x)+2π
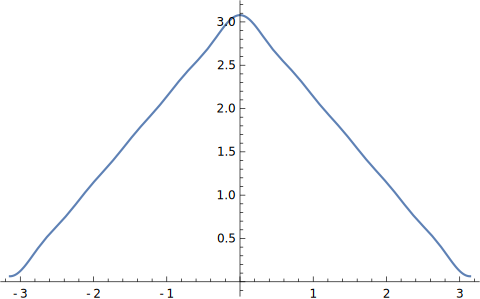
图象为
newpage
这个函数又更为接近原函数了.可见当我们添加更为高频的成分之后,函数越来越贴近原函数了.最后我们加入非常高的高平成分进去.
1 , s i n ( x ) , c o s ( x ) , ⋯ , s i n ( 99 x ) , c o s ( 99 x ) 1, sin(x), cos(x), cdots, sin(99x), cos(99x) 1,sin(x),cos(x),⋯,sin(99x),cos(99x)
求得的函数我就不列出来了,因为很长很复杂了.但是我们可以把它的图像输出出来.
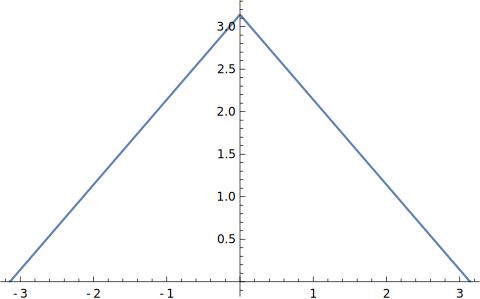
这下你凭借肉眼是看不出来这个函数和原函数的区别的.当我们将频率成分扩展到无限的时候.我们就能够得到一个傅里叶级数展开式组成的函数,它在数学上严格等于原函数.
一般周期傅里叶级数
如果一个函数的周期不是 2 π 2pi 2π怎么办?假如一个函数的周期为 2 l 2l 2l.那么这下该怎么办呢?其实也很容易的.我们可以将 2 l 2l 2l周期的函数变为 2 π 2pi 2π周期.如何做?换元法而已.我们来看看.如何使用换元法将一个周期为 2 l 2l 2l的函数换成一个周期为 2 π 2pi 2π的函数.
f ( x + 2 l ) = f ( x ) f(x+2l)=f(x) f(x+2l)=f(x)
只需要进行变换一下自变量就行了.
x
=
l
π
z
x=frac{l}{pi}z
x=πlz这样就可以了.然后我们可以换回来,就回到了原来的形式.这样我们可以得到如下的傅里叶系数展开式形式
a
0
2
+
∑
k
=
1
(
a
k
c
o
s
(
k
π
l
x
)
+
b
k
s
i
n
(
k
π
l
x
)
)
frac{a_0}{2}+sum_{k=1}(a_kcos(frac{kpi}{l}x)+b_ksin(frac{kpi}{l}x))
2a0+k=1∑(akcos(lkπx)+bksin(lkπx))
其中,
a
0
=
1
l
∫
−
l
l
f
(
x
)
d
x
a_0=frac{1}{l}int_{-l}^{l}{f(x)dx}
a0=l1∫−llf(x)dx
a
k
=
1
l
∫
−
l
l
f
(
x
)
c
o
s
(
k
π
l
x
)
d
x
a_k=frac{1}{l}int_{-l}^{l}{f(x)cos(frac{kpi}{l}x)dx}
ak=l1∫−llf(x)cos(lkπx)dx
b
k
=
1
l
∫
−
l
l
f
(
x
)
s
i
n
(
k
π
l
x
)
d
x
b_k=frac{1}{l}int_{-l}^{l}{f(x)sin(frac{kpi}{l}x)dx}
bk=l1∫−llf(x)sin(lkπx)dx
复数形式
傅里叶级数的复数形式和上面写出的三角函数形式没有本质区别.他们只是同样的数学概念的不同形式而已.可以互相转换.值得注意的是,我们讨论的 x x x自变量的取值范围属于 C Bbb{C} C不仅限于 R Bbb{R} R
下面我们就根据一般形式进行复数形式的推到,我们要用到的根据是欧拉公式
e i x = c o s ( x ) + s i n ( x ) i e^{ix}=cos(x)+sin(x)i eix=cos(x)+sin(x)i
那么我们可以根据欧拉公式进行转换
c
o
s
(
k
π
l
x
)
=
(
e
k
π
x
l
i
+
e
−
k
π
x
l
i
)
/
2
cos(frac{kpi}{l}x)=(e^{frac{kpi x}{l}i}+e^{-frac{kpi x}{l}i})/2
cos(lkπx)=(elkπxi+e−lkπxi)/2
s
i
n
(
k
π
l
x
)
=
−
(
e
k
π
x
l
i
−
e
−
k
π
x
l
i
)
i
/
2
sin(frac{kpi}{l}x)=-(e^{frac{kpi x}{l}i}-e^{-frac{kpi x}{l}i})i/2
sin(lkπx)=−(elkπxi−e−lkπxi)i/2
将上面的公式带入原来的级数里面我们整理可得.
a 0 2 + ∑ k = 1 ∞ [ a k − i b k 2 e k π x l i + a k + i b k 2 e − k π x l i ] frac{a_0}{2}+sum_{k=1}^{infty}left[ frac{a_k-ib_k}{2}e^{frac{kpi x}{l}i} + frac{a_k+ib_k}{2}e^{-frac{kpi x}{l}i}right] 2a0+k=1∑∞[2ak−ibkelkπxi+2ak+ibke−lkπxi]
你可以假设
c
0
=
a
0
2
,
c
n
=
a
k
−
i
b
k
2
,
c
−
n
=
a
k
+
i
b
k
2
c_0=frac{a_0}{2},c_{n}=frac{a_k-ib_k}{2},c_{-n}=frac{a_k+ib_k}{2}
c0=2a0,cn=2ak−ibk,c−n=2ak+ibk,并化简可得
c
n
=
1
2
l
∫
−
l
l
f
(
x
)
e
−
k
π
x
l
d
x
c_n=frac{1}{2l}int_{-l}^{l}{f(x)e^{-frac{kpi x}{l}}dx}
cn=2l1∫−llf(x)e−lkπxdx
c
−
n
=
1
2
l
∫
−
l
l
f
(
x
)
e
k
π
x
l
d
x
c_{-n}=frac{1}{2l}int_{-l}^{l}{f(x)e^{frac{kpi x}{l}}dx}
c−n=2l1∫−llf(x)elkπxdx
由此可见系数的形式可以统一为
c
n
=
1
2
l
∫
−
l
l
f
(
x
)
e
−
i
k
π
x
l
d
x
,
(
k
=
0
,
±
1
,
±
2
,
⋯
)
c_n=frac{1}{2l}int_{-l}^{l}{f(x)e^{-i frac{kpi x}{l}}dx},(k=0, pm 1, pm 2, cdots)
cn=2l1∫−llf(x)e−ilkπxdx,(k=0,±1,±2,⋯)
如此以来,傅里叶级数就可以变为更为简单的形式
∑ − ∞ ∞ c n e k π x l i sum_{-infty}^{infty}c_ne^{frac{kpi x}{l}i} −∞∑∞cnelkπxi
补充
-
刚才的例子里面并不含sin函数成分.是因为巧合.如果我们的函数更为一般些.图象更为复杂的话.里面一般都会含有sin函数成分.当然这是和函数 f ( x ) f(x) f(x)的奇偶性有关的.
-
傅里叶级数的展开式所含有的频率成分是固定的,而且是离散的.他们分别是.
-
对于有个函数,比如只有一个区域有定义,切满足傅里叶级数的收敛性质的函数.可以做延拓.也就是重复那个区段,就可以把它变成周期函数.然后进行傅里叶级数的变换.
1 2 π , 1 π , 3 2 π , 2 π , 5 2 π , ⋯ , n 2 π , ⋯ frac{1}{2pi},frac{1}{pi},frac{3}{2pi},frac{2}{pi},frac{5}{2pi}, cdots, frac{n}{2pi},cdots 2π1,π1,2π3,π2,2π5,⋯,2πn,⋯
傅里叶变换
有了傅里叶级数的基础最好趁热打铁,学习傅里叶变换.傅里叶级数有什么缺点呢?还是有的,比如对于定义在全数域上而没有周期的函数怎么办?接下来我们看看如何从傅里叶级数慢慢的导出傅里叶变换.
c
n
=
1
2
l
∫
−
l
l
f
(
x
)
e
−
i
n
π
x
l
d
x
,
(
n
=
0
,
±
1
,
±
2
,
⋯
)
c_n=frac{1}{2l}int_{-l}^{l}{f(x)e^{-i frac{npi x}{l}}dx},(n=0, pm 1, pm 2, cdots)
cn=2l1∫−llf(x)e−ilnπxdx,(n=0,±1,±2,⋯)
∑
−
∞
∞
c
n
e
k
π
x
l
i
sum_{-infty}^{infty}c_ne^{frac{kpi x}{l}i}
−∞∑∞cnelkπxi
对于一般周期的傅里叶级数,变换后的频率成分主要是
π l , 2 π l , ⋯ , k π l , ⋯ frac{pi}{l},frac{2pi}{l},cdots, frac{kpi}{l}, cdots lπ,l2π,⋯,lkπ,⋯
对于不同的周期 l l l,频率成分不一样.那么我们来举例看看.根据不同的 l l l来看看不同的傅里叶级数所含有的频率成分.
-
l = 1 l=1 l=1
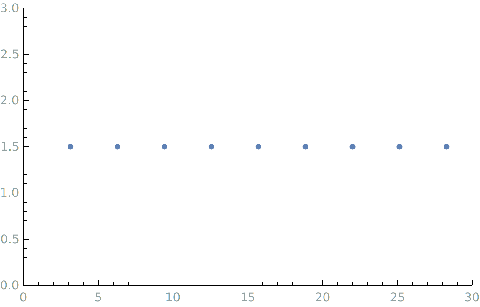
newpage
-
l = 2 l=2 l=2
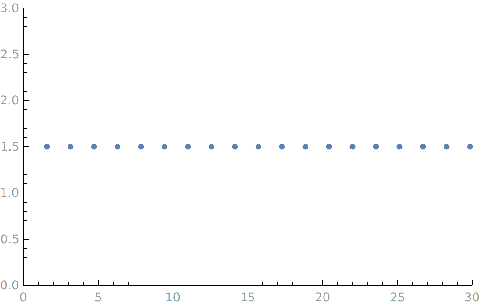
- l = 5 l=5 l=5
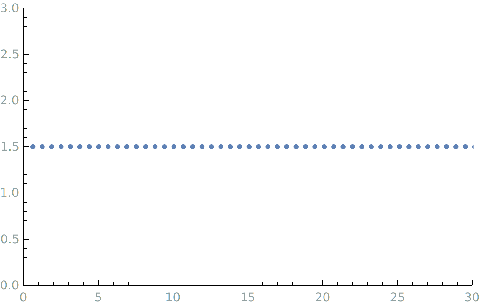
-
l = 20 l=20 l=20
由此可见,当周期趋近于无穷大的时候.傅里叶级数将会包含所有的频率成分.变成一个连续的频率成分.我们看看如何将傅里叶级数变成连续的.
其实也不难,就是取极限.
f
(
x
)
=
lim
l
→
∞
∑
−
∞
∞
[
c
n
e
k
π
x
l
i
]
f(x)=lim_{lrightarrow infty} sum_{-infty}^{infty} left[ c_ne^{frac{kpi x}{l}i} right]
f(x)=l→∞lim−∞∑∞[cnelkπxi] 把
c
n
c_n
cn也带入进去可得.
f
(
x
)
=
lim
l
=
∞
∑
k
=
−
∞
∞
[
(
1
2
l
∫
−
l
l
f
(
t
)
e
−
i
k
π
t
l
d
t
)
e
k
π
x
l
i
]
f(x)=lim_{l=infty}sum_{k=-infty}^{infty} left[ (frac{1}{2l}int_{-l}^{l}{f(t)e^{-i frac{kpi t}{l}}dt}) e^{frac{kpi x}{l}i} right]
f(x)=l=∞limk=−∞∑∞[(2l1∫−llf(t)e−ilkπtdt)elkπxi] 进行化简
f ( x ) = lim l → ∞ ∑ k = − ∞ ∞ [ 1 2 l ∫ − l l f ( t ) e ( x − t ) π k l d t ] f(x)=lim_{lrightarrow infty} sum_{k=-infty}^{infty} left[ frac{1}{2l}int_{-l}^{l}{f(t)e^{frac{(x-t)pi k}{l}}dt} right] f(x)=l→∞limk=−∞∑∞[2l1∫−llf(t)el(x−t)πkdt]
我们现在来看看引入一个变量 λ k = k π l lambda_k=frac{kpi}{l} λk=lkπ.这个正是频率成分. Δ λ = λ n + 1 − λ n = π l Deltalambda=lambda_{n+1}-lambda_n=frac{pi}{l} Δλ=λn+1−λn=lπ.我们带入上面的式子.
f ( x ) = lim l → ∞ ∑ k = − ∞ ∞ [ 1 2 π ∫ − l l f ( t ) e λ k i ( x − t ) d t ] Δ λ f(x)=lim _{l rightarrow infty} sum_{k=-infty}^{infty}left[frac{1}{2 pi} int_{-l}^{l} f(t) e^{lambda_{k} i(x-t)} d tright] Delta lambda f(x)=l→∞limk=−∞∑∞[2π1∫−llf(t)eλki(x−t)dt]Δλ
当
l
→
∞
l rightarrow infty
l→∞.我们可以得
f
(
x
)
=
1
2
π
∫
−
∞
∞
∫
−
∞
∞
f
(
t
)
e
i
λ
(
x
−
t
)
d
t
d
λ
f(x)=frac{1}{2 pi} int_{-infty}^{infty} int_{-infty}^{infty} f(t) e^{i lambda(x-t)} d t d lambda
f(x)=2π1∫−∞∞∫−∞∞f(t)eiλ(x−t)dtdλ
整理一下,我们可以得到下面的式子
f
(
x
)
=
1
2
π
∫
−
∞
∞
(
1
2
π
∫
−
∞
∞
f
(
t
)
e
−
i
λ
t
d
t
)
e
i
λ
x
d
λ
f(x)=frac{1}{sqrt{2 pi}} int_{-infty}^{infty}left(frac{1}{sqrt{2 pi}} int_{-infty}^{infty} f(t) e^{-i lambda t} d tright) e^{i lambda x} d lambda
f(x)=2π1∫−∞∞(2π1∫−∞∞f(t)e−iλtdt)eiλxdλ
我们把里面的一个部分
f
^
(
λ
)
=
1
2
π
∫
−
∞
∞
f
(
t
)
e
−
i
λ
t
d
t
hat{f}(lambda)=frac{1}{sqrt{2pi}} int_{-infty}^{infty}{f(t)e^{-ilambda t}dt}
f^(λ)=2π1∫−∞∞f(t)e−iλtdt
叫做傅里叶变换
我们来比较一下在傅里叶级数中的 c n c_n cn和傅里叶变换中的 f ^ ( λ ) hat{f}(lambda) f^(λ)
-
c n = 1 2 l ∫ − l l f ( x ) e − i n π x l d x , ( n = 0 , ± 1 , ± 2 , ⋯ ) c_n=frac{1}{2l}int_{-l}^{l}{f(x)e^{-i frac{npi x}{l}}dx},(n=0, pm 1, pm 2, cdots) cn=2l1∫−llf(x)e−ilnπxdx,(n=0,±1,±2,⋯)
-
f ^ ( λ ) = 1 2 π ∫ − ∞ ∞ f ( t ) e − i λ t d t hat{f}(lambda)=frac{1}{sqrt{2pi}} int_{-infty}^{infty}{f(t)e^{-ilambda t}dt} f^(λ)=2π1∫−∞∞f(t)e−iλtdt
可见傅里叶级数中的系数在周期无穷大的情况下就会,变成傅里叶变换的形式.傅里叶变换的这个函数值代表的是什么意思?
f ^ ( λ ) = 1 2 π ∫ − ∞ ∞ f ( t ) e − i λ t d t hat{f}(lambda)=frac{1}{sqrt{2pi}} int_{-infty}^{infty}{f(t)e^{-ilambda t}dt} f^(λ)=2π1∫−∞∞f(t)e−iλtdt
这个函数是一个以
λ
lambda
λ为自变量的一个函数.这个自变量就是代表的物理意义是频率.而函数求得值是什么呢?它是一个复数.复数怎么来解释?这个需要将复数形式还原为实数的形式.当我们的原函数
f
(
x
)
f(x)
f(x)是一个定义在实数域上的信号的时候.我们怎么来解释
f
^
(
λ
)
=
1
2
π
∫
−
∞
∞
f
(
t
)
e
−
i
λ
t
d
t
hat{f}(lambda)=frac{1}{sqrt{2pi}} int_{-infty}^{infty}{f(t)e^{-ilambda t}dt}
f^(λ)=2π1∫−∞∞f(t)e−iλtdt
我们来看看如何重新根据
f
^
(
λ
)
hat{f}(lambda)
f^(λ)计算振幅和频率成分.
f
^
(
λ
)
=
1
2
π
∫
−
∞
∞
f
(
t
)
e
−
i
λ
t
d
t
↦
e
i
λ
x
hat{f}(lambda)=frac{1}{sqrt{2pi}} int_{-infty}^{infty}{f(t)e^{-ilambda t}dt} mapsto e^{ilambda x}
f^(λ)=2π1∫−∞∞f(t)e−iλtdt↦eiλx
f
^
(
−
λ
)
=
1
2
π
∫
−
∞
∞
f
(
t
)
e
i
λ
t
d
t
↦
e
−
i
λ
x
hat{f}(-lambda)=frac{1}{sqrt{2pi}} int_{-infty}^{infty}{f(t)e^{ilambda t}dt} mapsto e^{-ilambda x}
f^(−λ)=2π1∫−∞∞f(t)eiλtdt↦e−iλx
将后面的项展开可得
f
^
(
λ
)
c
o
s
(
λ
x
)
+
i
f
^
(
λ
)
s
i
n
(
λ
x
)
hat{f}(lambda)cos(lambda x)+ihat{f}(lambda) sin(lambda x)
f^(λ)cos(λx)+if^(λ)sin(λx)
f
^
(
−
λ
)
c
o
s
(
λ
x
)
−
i
f
^
(
−
λ
)
s
i
n
(
λ
x
)
hat{f}(-lambda)cos(lambda x)-ihat{f}(-lambda) sin(lambda x)
f^(−λ)cos(λx)−if^(−λ)sin(λx)
合并同类项可得
(
f
^
(
λ
)
+
f
^
(
−
λ
)
)
c
o
s
(
λ
x
)
+
i
(
f
^
(
λ
)
−
f
^
(
−
λ
)
)
s
i
n
(
λ
x
)
(hat{f}(lambda)+hat{f}(-lambda))cos(lambda x)+i(hat{f}(lambda)-hat{f}(-lambda))sin(lambda x)
(f^(λ)+f^(−λ))cos(λx)+i(f^(λ)−f^(−λ))sin(λx)
又因为
f
^
(
λ
)
+
f
^
(
−
λ
)
=
1
2
π
∫
−
∞
∞
f
(
t
)
c
o
s
(
λ
t
)
d
t
hat{f}(lambda)+hat{f}(-lambda)=frac{1}{sqrt{2pi}}int_{-infty}^{infty}{f(t)cos(lambda t)dt}
f^(λ)+f^(−λ)=2π1∫−∞∞f(t)cos(λt)dt
f
^
(
λ
)
−
f
^
(
−
λ
)
=
−
i
1
2
π
∫
−
∞
∞
f
(
t
)
s
i
n
(
λ
t
)
d
t
hat{f}(lambda)-hat{f}(-lambda)=-ifrac{1}{sqrt{2pi}}int_{-infty}^{infty}{f(t)sin(lambda t)dt}
f^(λ)−f^(−λ)=−i2π1∫−∞∞f(t)sin(λt)dt
所以,我们可以最终得到一个不含虚数的展开式的两相.
1
2
π
∫
−
∞
∞
f
(
t
)
c
o
s
(
λ
t
)
d
t
c
o
s
(
λ
x
)
+
1
2
π
∫
−
∞
∞
f
(
t
)
s
i
n
(
λ
t
)
d
t
s
i
n
(
λ
x
)
frac{1}{sqrt{2pi}}int_{-infty}^{infty}{f(t)cos(lambda t)dt}cos(lambda x)+frac{1}{sqrt{2pi}}int_{-infty}^{infty}{f(t)sin(lambda t)dt} sin(lambda x)
2π1∫−∞∞f(t)cos(λt)dtcos(λx)+2π1∫−∞∞f(t)sin(λt)dtsin(λx)
这就可以复原出两个频率相同的正余弦信号.
傅里叶变换举例
-
f ( x ) = s i n ( x ) f(x)=sin(x) f(x)=sin(x)
-
傅里叶变换的结果
f ^ ( λ ) = − i π 2 δ ( λ − 1 ) + i π 2 δ ( λ + 1 ) hat{f}(lambda)=-i sqrt{frac{pi }{2}} delta (lambda -1)+i sqrt{frac{pi }{2}} delta (lambda +1) f^(λ)=−i2πδ(λ−1)+i2πδ(λ+1) -
完整的 f ( x ) f(x) f(x)形式为
f ( x ) = 1 2 π ∫ − ∞ ∞ [ − i π 2 δ ( λ − 1 ) + i π 2 δ ( λ + 1 ) ] e i λ x d λ f(x)=frac{1}{sqrt{2pi}}int_{-infty}^{infty}{left[-i sqrt{frac{pi }{2}} delta (lambda -1)+i sqrt{frac{pi }{2}} delta (lambda +1)right]e^{ilambda x}dlambda} f(x)=2π1∫−∞∞[−i2πδ(λ−1)+i2πδ(λ+1)]eiλxdλ
我们化一下简得 f ( x ) = 1 2 π [ − i π 2 e i ⋅ 1 ⋅ x + i π 2 e i ⋅ − 1 ⋅ x ] f(x)=frac{1}{sqrt{2pi}} left[ -i sqrt{frac{pi}{2}}e^{i cdot 1 cdot x}+i sqrt{frac{pi}{2}} e^{icdot -1 cdot x} right] f(x)=2π1[−i2πei⋅1⋅x+i2πei⋅−1⋅x] 再次化简可得 f ( x ) = s i n ( x ) f(x)=sin(x) f(x)=sin(x)
注意所谓的 δ ( x ) delta(x) δ(x)是个什么函数.它的定义其实很简单.他的性质如下 δ ( x ) = 0 , x ≠ 0 delta(x)=0, xneq 0 δ(x)=0,x=0时 δ ( x ) = ∞ , x = 0 delta(x)=infty, x=0 δ(x)=∞,x=0.另外 ∫ − ∞ ∞ δ ( x ) f ( x ) d x = f ( 0 ) int_{-infty}^{infty}{delta(x)f(x)dx}=f(0) ∫−∞∞δ(x)f(x)dx=f(0).
-
-
f ( x ) = x f(x)=x f(x)=x
-
傅里叶变换得
f ^ ( λ ) = i 2 π δ ′ ( λ ) hat{f}(lambda)=i sqrt{2 pi } delta '(lambda ) f^(λ)=i2πδ′(λ) -
那么傅里叶逆变换的完整性时为
f ( x ) = 1 2 π ∫ − ∞ ∞ f ^ ( x ) e i λ x d λ f(x)=frac{1}{sqrt{2pi}}int_{-infty}^{infty}{hat{f}(x)e^{ilambda x}dlambda} f(x)=2π1∫−∞∞f^(x)eiλxdλ积分过程如下
-
∫ − ∞ ∞ i δ ′ ( λ ) e i λ x d λ int_{-infty}^{infty} i delta^{prime}(lambda) e^{i lambda x} d lambda ∫−∞∞iδ′(λ)eiλxdλ
-
i [ ∫ − ∞ ∞ δ ( λ ) e i λ x d λ − i x ∫ − ∞ ∞ δ ( λ ) e i λ x d λ ] i left[ int_{-infty}^{infty}{delta(lambda)e^{ilambda x}dlambda}-ix int_{-infty}^{infty}{delta(lambda)e^{ilambda x}dlambda} right] i[∫−∞∞δ(λ)eiλxdλ−ix∫−∞∞δ(λ)eiλxdλ]
-
i ( e 0 − i x e 0 ) = x i(e^{0}-ixe^{0})=x i(e0−ixe0)=x
-
-
最终结果是 f ( x ) = x f(x)=x f(x)=x
-
最后
以上就是欣喜发箍最近收集整理的关于线性代数观点来看傅里叶级数和傅里叶变换基本定义傅里叶级数傅里叶变换的全部内容,更多相关线性代数观点来看傅里叶级数和傅里叶变换基本定义傅里叶级数傅里叶变换内容请搜索靠谱客的其他文章。








发表评论 取消回复