文章目录
- 1. 进制的定义
- 2. 进制的规范
- 3. 进制的进位运算
- 3.1 十进制
- 3.2 二进制
- 3.3 八进制
- 3.4 十六进制
- 3.5 进制表
- 4. 进制的相互转换
- 4.1 二进制与十进制的相互转化
- 4.2 二进制与十六进制的相互转换
- 4.3 十进制与十六进制的相互转换
- 5. 人类为什么最习惯用十进制
- 6. 计算机为什么用的是二进制
- 小结
1. 进制的定义
首先我们需要先了解什么是进制?进制是学习计算机语言最基本的知识,所以一定要掌握。其实它很简单,我们日常生活中有很多进制的例子,例如:
- 一分钟六十秒,逢六十进一,就是六十进制;
- 一天二十四小时,逢二十四进一,就是二十四进制;
- 一星期七天,逢七进一,就是七进制;
- 一年十二个月,逢十二进一,就是十二进制;
- 小学数学是逢十进一,就是十进制;
- 而计算机中的数据只有 0 和 1,逢二进一,就是二进制。
所以进制就是逢几进一,r 进制就是逢 r 进一。计算机只能识别二进制,人类最习惯使用的是十进制,而为了实际需要,又建立了八进制和十六进制。八进制就是逢八进一,十六进制就是逢十六进一。
2. 进制的规范
C语言中规定了八进制数前面要加0(注意是数字零而不是字母 o),十六进制数前面要加0x或0X,而十进制前面什么都不加。这是为什么呢?
比如 5,到底是十进制、八进制还是十六进制?什么都不加就默认是十进制。如果希望 5 是八进制,那么前面就加上 0;如果希望 5 是十六进制,那么前面就加上0x或0X。
3. 进制的进位运算
3.1 十进制
十进制为逢十进一,它只有 0、1、2、3、4、5、6、7、8、9 这十个基数。逢十进一的意思就是:9 再加 1 就变为 10,即向十位进了一位,原来个位回归 0。
3.2 二进制
二进制为逢二进一,它只有 0 和 1 两个基数。逢二进一的意思就是:
- 1 再加 1 就变成 10,即向前进了一位,原来的 1 变成 0;
- 再加 1 就是 11;
- 再加 1 又逢二,再往前进一位,进一位后第二个 1 又逢二再进位,就是 100 了;
- 再加 1 变成 101,再加 1 变成 110,再加 1 变成 111,再加 1 变成 1000……
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 二进制 | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 |
无论是十进制、二进制、八进制还是十六进制,都只是计数的一种方式,只不过它们用的是不同的进制,所以表现形式不一样,但本质上都是同一个数字。理解了上面内容,后面很多知识就很容易理解了。
3.3 八进制
八进制就是逢八进一,它只有 0、1、2、3、4、5、6、7 这八个基数。
由上可以总结出,r 进制有 r 个基数,而且基数里面最大的是 r–1,因为基数都是从 0 开始的。比如五进制中,基数最大的是 4,基数分别为 0、1、2、3、4。
3.4 十六进制
十六进制肯定有十六个基数。它的基数除了十进制的 0~9 之外,还有字母 A~F,总共加起来是十六个。注意,字母不区分大小写。十六进制是逢十六进一,F 是十五,加 1 就变成十六了,逢十六就进一,即0x10。
3.5 进制表
下面是常用进制对照表,大家可以看一下。
| 十进制 | 二进制 | 八进制 | 十六进制 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
4. 进制的相互转换
从上面的介绍我们知道了进制只是数字的不同表现形式,它们本质上表示的是同一个数。那么既然是同一个数,进制之间可不可以相互转换呢?答案是肯定的。下面我们就对二进制、十进制、十六进制进行相互转换,让大家更清晰的了解进制。
4.1 二进制与十进制的相互转化
-
十进制转二进制的转换原理:除以2,反向取余数,直到商为0终止。
例如:9(十进制)→1001(二进制),转换过程如下图:

-
二进制转十进制的转换原理: 就是用进制的定义:二进制的每一个乘以2的n次方,n从0开始,每次递增1。然后得出来的每个数相加。
例如:1110(二进制)→ 14(十进制) ,转换过程:
1 ∗ 2 3 + 1 ∗ 2 2 + 1 ∗ 2 1 + 0 ∗ 2 0 = 14 1*2^3+1*2^2+1*2^1+0*2^0=14 1∗23+1∗22+1∗21+0∗20=14
推荐记住2的指数9以内的数:1、2、4、8、16、32、64、128、256、1024。 -
负数:这时候需引入补码的概念,一个byte第八位(最前位)是确定符号的位,0为正,1为负,但考虑到+0与-0值相等,为了使逻辑成立没有偏差,所以提出了补码表示法。
补码的计算公式:
正数:源码、反码和补码都相同。
负数:补码 = 反码(符号位保持不变) + 1
注意: 负数在计算补码的时候,在源码取反的过程中要保留符号位不变,其他位取反,例如:10001010取反11110101(第一个1不变),补码就为11110110。
注意:
看一个二进制是否是正数还是负数,需要先说明其是存储在计算机中,然后要搞清楚其在计算机中是以有符号进行存储还是无符号进行存储。
-
如果是无符号存储,则其为一个正数。
-
若是有符号存储,则为补码存储。
(补码存储)需要看其最高位,最高位为0,为正数; 反之,为负数。
如果仅仅是给了一堆二进制:比如10101010,你如果不说是在哪存的?那么它是没有正负概念的。
-
-
小数
- 十进制的小数转换为二进制,主要是小数部分乘以2,取整数部分依次从左往右放在小数点后,直至小数点后为0。例如十进制的0.125,要转换为二进制的小数,结果就是0.001。

-
二进制的小数转换为十进制主要是乘以2的负次方,从小数点后开始,依次乘以2的负一次方,2的负二次方,2的负三次方等。例如二进制数0.001转换为十进制,结果就是0.125。
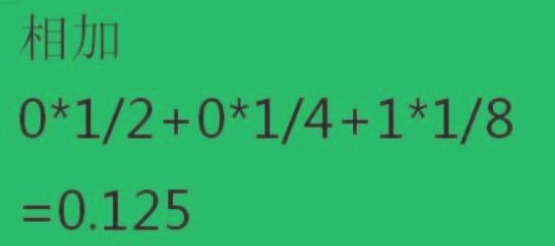
4.2 二进制与十六进制的相互转换
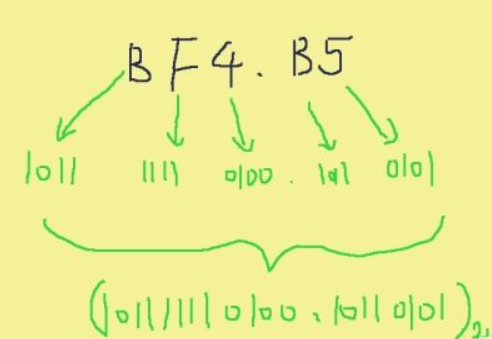
二进制转换成十六进制的方法是,取四合一法,即从二进制的小数点为分界点,向左(或向右)每四位取成一位。需要注意的是,在向左(或向右)取四位时,取到最高位(最低位)如果无法凑足四位,就可以在小数点的最左边(或最右边)补0,进行换算。
**注意:**16进制的表示法,用字母H后缀表示,比如BH就表示16进制数11;也可以用0X前缀表示,比如0X23就是16进制的23
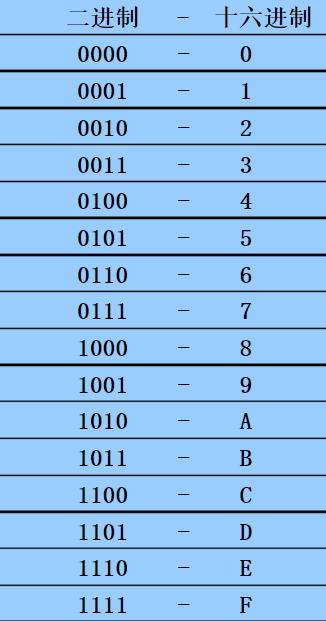
这个转换比较简单,只需要记好二进制数的每四位对应一个16进制数,就能轻易的转换。而他们的对应关系在上面的进制表里也写的很清楚,为了方便理解,我再把对应关系放在下面:
举个例子:
4.3 十进制与十六进制的相互转换
进行转换之前,先要知道十六进制与十进制的区别和表示方法:

-
十进制转十六进制(方式一)
可以采取十进制转二进制那种方式,也就是整除取余法,例如:

-
十进制转十六进制(方式二)
十进制数转化为十六进制数可以先转二进制再转十六进制,例如:

-
十六进制转十进制
这和二进制转十进制相似,例如:
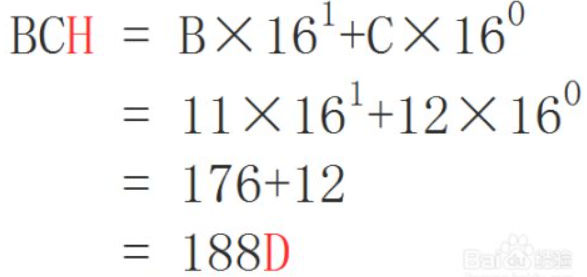
5. 人类为什么最习惯用十进制
人类为什么最习惯用逢十进一的十进制?对于世界上大部分的国家,即便之前因为交通不发达,他们彼此之间并不知道在世界的某一个角落还有另一个民族的存在,但是他们使用的都是十进制!这是为什么?
原因很简单,就是因为我们都有十个手指!进制的起源是用于记数的,人类刚开始都是用手指计数的。即使是现在的小朋友算数也还是喜欢用手指,所以人类最习惯用十进制。
6. 计算机为什么用的是二进制
那么为什么计算机使用的是二进制呢?
因为二进制从硬件上比较容易实现。任何事物最少也有两种不同的状态,所以区分成两种状态比较容易。但是要将一个硬件硬生生地区分成十种不同的状态,这个就太难、太复杂了。
小结
进制是学习计算机必须要掌握的内容,也是一个重点。
- 掌握进制的概念,区分八进制数、十进制数和十六进制数的表示方法。注意八进制数是以
0开头,十六进制数是以0x或0X开头,以及了解其原因。 - 掌握进制只是数字的不同表现形式,它们本质上表示的是同一个数。
- 了解为什么人类习惯使用十进制而计算机使用的却是二进制。
- 掌握进制间的相互转化
最后
以上就是含蓄画板最近收集整理的关于编程基础 进制的定义,二进制、十进制、十六进制的相互转换的全部内容,更多相关编程基础内容请搜索靠谱客的其他文章。






![C语言输入两个十进制的数用二进制算法相加,[PHP] 算法-两个n位的二进制整数相加问题PHP实现...](https://www.shuijiaxian.com/files_image/reation/bcimg10.png)

发表评论 取消回复