由于在看论文的时候设涉及批量归一化的知识,所以决定提前学这一节。
那么进行归一化有什么好处呢?
原因在于神经网络学习过程本质就是为了学习数据分布,一旦训练数据与测试数据的分布不同,那么网络的泛化能力也大大降低;另外一方面,一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度。
批量归一化(batch normalization)的提出是为了解决对深层神经网络,即使输入数据已做标准化,训练中模型参数的更新依然很容易造成靠近输出层输出的剧烈变化的问题。
BN算法(Batch Normalization)其强大之处如下:
- 可以选择比较大的初始学习率,让训练速度飙涨,因为它具有快速训练收敛的特性;
- 改善正则化策略:作为正则化的一种形式,轻微减少了对dropout的需求
再也不用去理会过拟合中drop out、L2正则项参数的选择问题,因为BN具有提高网络泛化能力的特性; - 再也不需要使用使用局部响应归一化层了(局部响应归一化是Alexnet网络用到的方法),因为BN本身就是一个归一化网络层;
- 可以把训练数据彻底打乱。
(一)批量归一化层
对全连接层进行批量归一化操作:
我们将批量归一化层置于全连接层中的仿射变换和激活函数之间。
也就是说,对于全连接层的输入u,先进行 x=W*u+b 的操作,然后对x进行批量归一化操作BN(x),对于输出再进行激活得到 φ(BN(x))。
批量归一化操作的过程如下:
对于有m个输入的小批量数据,仿射变换得到一组输出新的小批量B={x(1),…,x(m)},这就是批量归一化层的输入,然后 y(i)=BN(x(i))的操作过程如下:
对这组x求得均值,方差,归一化操作后,利用可以学习的参数γ和x进行逐元素相乘并与β相加。这样我们就得到了x(i)经过批量归一化层的输出y(i)。
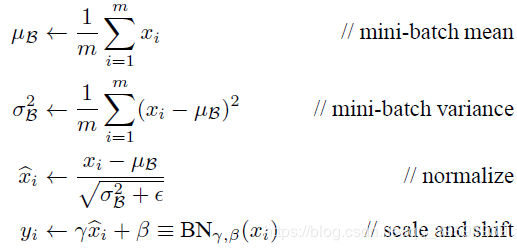
解释一下ε,γ和β的意义:
ϵ>0是一个很小的常数,保证分母大于0。拉伸(scale)参数 γ 和偏移(shift)参数 β。这两个参数和x(i)形状相同,皆为d维向量。
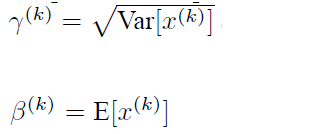
引入了这个可学习重构参数γ、β,让我们的网络可以学习恢复出原始网络所要学习的特征分布。最后Batch Normalization网络层的前向传导过程公式就是:

 所以说这样处理以后,就是不仅进行了归一化操作还恢复了x的特征分布。
所以说这样处理以后,就是不仅进行了归一化操作还恢复了x的特征分布。
需要注意的特殊情况:
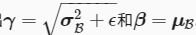
此时批量归一化无益,理论上,学出的模型可以不使用批量归一化。
对卷积层做批量归一化操作:
对卷积层来说,批量归一化发生在卷积计算之后、应用激活函数之前。
如果卷积计算输出多个通道,我们需要对这些通道的输出分别做批量归一化,且每个通道都拥有独立的拉伸和偏移参数,并均为标量。
卷积神经网络经过卷积后得到的是一系列的特征图,如果min-batch sizes为m,那么网络某一层输入数据可以表示为四维矩阵(m,f,w,h),m为min-batch sizes,f为特征图个数,w、h分别为特征图的宽高。在CNN中我们可以把每个特征图看成是一个特征处理(一个神经元),因此在使用Batch Normalization,mini-batch size 的大小就是:mwh,于是对于每个特征图都只有一对可学习参数:γ、β。说白了吧,这就是相当于求取所有样本所对应的一个特征图的所有神经元的平均值、方差,然后对这个特征图神经元做归一化。
预测和训练时的批量归一化:
对于预测时,一般把批量取大一点,从而得到较为准确的均值和方差。
训练时,为了使得任意输入都有相同的输出,我们通过移动平均估算整个训练数据集的样本均值和方差,而不选择小批量的均值方差,并在预测时使用它们得到确定的输出。
(二)从零开始实现
有一些预备知识先解释一下:
①关于python中assert的用法:
assert用来声明某个条件是真的,格式为
assert expression
当assert语句失败时,会引发AssertionError。
比如当我们确信列表中有至少一个元素,我们可以用assert语句来检验,当没有时就会引发错误。
②关于mean函数的用法:
mxnet.ndarray.mean(data=None, axis=_Null, keepdims=_Null, exclude=_Null, out=None, name=None, **kwargs)
# Computes the mean of array elements over given axes.
主要是要举几个例子直观的说明一下axis和keepdims的用法:
首先看最简单的二维数组
axis:执行缩减的一个或多个轴
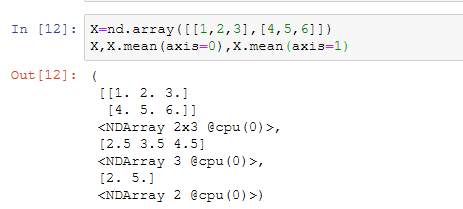
keepdims:如果设置为true,缩小的轴将作为尺寸为1的尺寸留在结果中。
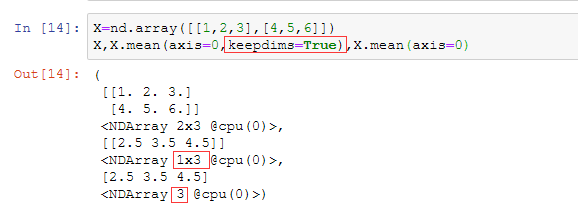
接着看三维的数组:
没有keepdims时,只看axis

axis=1,keepdims对比
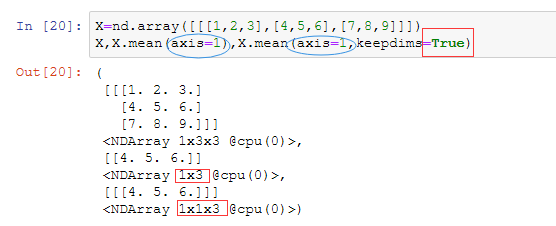
axis=2,keepdims对比
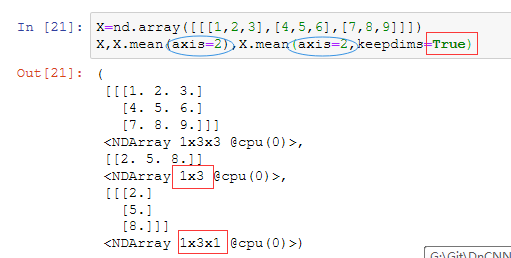
axis不止一个时,可以看到等效为多次求mean:
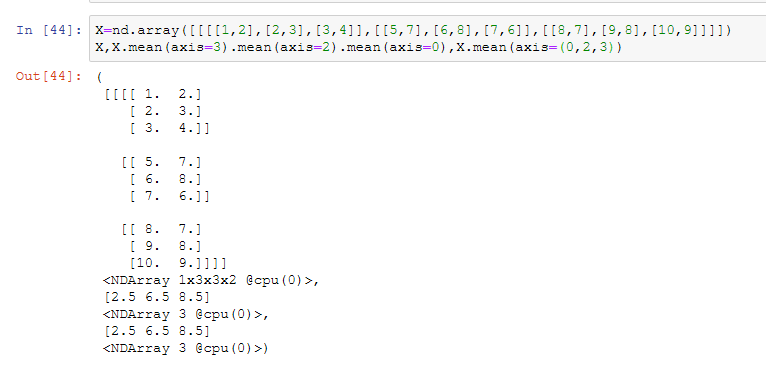
分步过程如下图:
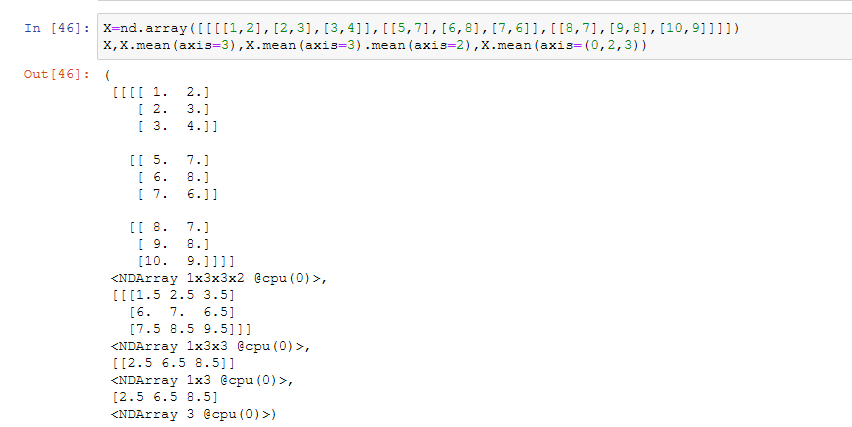
个人感觉直观的看到axis和mean的用法比讲解更有效。
③momentum的用法:
假设A为起始点,首先计算A点的梯度∇a ,然后下降到B点,
θnew=θ−α∇a,θ 为参数α 为学习率。
到了B点需要加上A点的梯度,这里梯度需要有一个衰减值γ,推荐取0.9。这样的做法可以让早期的梯度对当前梯度的影响越来越小,如果没有衰减值,模型往往会震荡难以收敛,甚至发散。所以B点的参数更新公式是这样的:
vt=γvt−1+α∇b,θnew=θ−vt (γ为衰减率,α为学习率)
其中vt−1表示之前所有步骤所累积的动量和。
动量方法主要是为了解决Hessian矩阵病态条件问题的,直观上讲就是,要是当前时刻的梯度与历史时刻梯度方向相似,这种趋势在当前时刻则会加强;要是不同,则当前时刻的梯度方向减弱。
有了这些预备知识后,再去对代码进行分析。
定义batch_norm()函数:
import d2lzh as d2l
from mxnet import autograd, gluon, init, nd
from mxnet.gluon import nn
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 通过autograd来判断当前模式是训练模式还是预测模式
if not autograd.is_training():
# 如果是在预测模式下,直接使用传入的移动平均所得的均值和方差
X_hat = (X - moving_mean) / nd.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4) # X的维度一定是2和4中的一个
if len(X.shape) == 2: # 如果是简单的二维情况
# 使用全连接层的情况,计算特征维上的均值和方差
mean = X.mean(axis=0)
# 由于axis为0,根据上面的图解,我们可以推出这是对批量归一化层的输入x的同一位置数求均值,
# 分母为批量大小,与之前的公式一致
var = ((X - mean) ** 2).mean(axis=0) #求方差
else:
# 使用二维卷积层的情况,计算通道维上(axis=1)的均值和方差。这里我们需要保持
# X的形状以便后面可以做广播运算
mean = X.mean(axis=(0, 2, 3), keepdims=True)
#通过令axis=(0,2,3),可以理解为mean=X.mean(axis=3).mean(axis=2).mean(axis=0)
#但是保持了维度是1*通道*1*1
#第1,,3,4维度求平均后得到的是某通道单个图片的均值,与我们的公式相符
var = ((X - mean) ** 2).mean(axis=(0, 2, 3), keepdims=True) # 同样求得方差
X_hat = (X - mean) / nd.sqrt(var + eps) # 训练模式下用当前的均值和方差做标准化
# 更新移动平均的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta # 拉伸参数gamma和偏移参数beta
return Y, moving_mean, moving_var
自定义一个BatchNorm层:
class BatchNorm(nn.Block):
def __init__(self, num_features, num_dims, **kwargs):
super(BatchNorm, self).__init__(**kwargs)
if num_dims == 2:
shape = (1, num_features) # 如果是一个二维的数组,num_features就是输出个数
else:
shape = (1, num_features, 1, 1) # 如果是一个四维的数组,num_features就是输出通道数(图像的特征图数目)
self.gamma = self.params.get('gamma', shape=shape, init=init.One())
# 参与求梯度和迭代的拉伸和偏移参数,分别初始化成1和0
self.beta = self.params.get('beta', shape=shape, init=init.Zero())
self.moving_mean = nd.zeros(shape)
# 不参与求梯度和迭代的变量,全在内存上初始化成0
self.moving_var = nd.zeros(shape)
def forward(self, X):
if self.moving_mean.context != X.context: # 如果X不在内存上,将moving_mean和moving_var复制到X所在显存上
self.moving_mean = self.moving_mean.copyto(X.context)
self.moving_var = self.moving_var.copyto(X.context)
Y, self.moving_mean, self.moving_var = batch_norm(
X, self.gamma.data(), self.beta.data(), self.moving_mean,
self.moving_var, eps=1e-5, momentum=0.9)
# 保存更新过的moving_mean和moving_var
return Y
(三)使用批量归一化层的LeNet
net = nn.Sequential()
net.add(nn.Conv2D(6, kernel_size=5), # 卷积层
BatchNorm(6, num_dims=4), #批量归一化层
nn.Activation('sigmoid'), # 激活函数
nn.MaxPool2D(pool_size=2, strides=2), # 最大池化层
nn.Conv2D(16, kernel_size=5),
BatchNorm(16, num_dims=4),
nn.Activation('sigmoid'),
nn.MaxPool2D(pool_size=2, strides=2),
nn.Dense(120), # 全连接层
BatchNorm(120, num_dims=2), # 批量归一化层
nn.Activation('sigmoid'), # 激活函数
nn.Dense(84),
BatchNorm(84, num_dims=2),
nn.Activation('sigmoid'),
nn.Dense(10))
训练修改后的模型:
lr, num_epochs, batch_size, ctx = 1.0, 5, 256, d2l.try_gpu()
#学习率lr设为1,学习周期为5,小批量大小为256,ctx判断用cpu还是Gpu
net.initialize(ctx=ctx, init=init.Xavier())
#对于权值采用Xavier初始化
trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': lr})
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size) # 下载数据集
d2l.train_ch5(net, train_iter, test_iter, batch_size, trainer, ctx,
num_epochs)
与我们刚刚自己定义的BatchNorm类相比,Gluon中nn模块定义的BatchNorm类使用起来更加简单。它不需要指定自己定义的BatchNorm类中所需的num_features和num_dims参数值。
最后
以上就是鳗鱼金鱼最近收集整理的关于《动手学深度学习》第十七天---批量归一化的全部内容,更多相关《动手学深度学习》第十七天---批量归一化内容请搜索靠谱客的其他文章。








发表评论 取消回复