2019 百度之星初赛三 补题

B.hdu6714 最短路2(最短路/dijkstra+floyd理解)

题目

在Floyd中，记dis[i][j]中最后一次松弛i到j的最短路的点的编号为x，且令d[i][j]=x

求，n<=1e3，m<=2e3

思路来源

https://blog.csdn.net/a1097304791/article/details/100067541

题解

对每个点暴力dijkstra，把复杂度从降到

注意当i到j之间的最短路，只有一条边的时候，d[i][j]为0

所以，d[i][j]中间，应该不考虑等于i或等于j的节点

多条最短路的时候，记录更新节点号最小的那条

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
typedef long long ll;
const int mod=998244353;
const int N=1e3+10; 
const int M=2e3+10;
int t,n,m,u,v,w;
int head[N],ans[N],cnt;
bool vis[N];
ll dis[N],res; 
struct edge{int to,nex;ll w;}e[M*2];
struct node
{
  ll w;
  int v;
  node(ll a,int c):w(a),v(c){
  } 
};
bool operator>(node a,node b)
{
	return a.w>b.w;
}
priority_queue<node,vector<node>,greater<node> >q;
void init()
{
	cnt=0;
	memset(head,0,sizeof head);
}
void add(int u,int v,ll w)
{
	e[++cnt].to=v;
	e[cnt].w=w;
	e[cnt].nex=head[u];
	head[u]=cnt;
}
void dijkstra(int s)
{
	memset(vis,0,sizeof vis);
	memset(ans,0,sizeof ans);
	for(int i=1;i<=n;++i)
	dis[i]=1e18;
	q.push(node(0,s));//说明从哪条边转移到这点的 
	dis[s]=0;
	while(!q.empty())
	{
		node tmp=q.top();
		q.pop();
		int v=tmp.v;
		if(vis[v])continue;
		vis[v]=1;
		for(int i=head[v];i;i=e[i].nex)
		{
			int to=e[i].to;
			ll w=e[i].w;
			if(dis[to]>dis[v]+w)
			{
				dis[to]=dis[v]+w;
				if(v!=s)ans[to]=max(ans[v],v);
				q.push(node(dis[to],to));
			}
			else if(dis[to]==dis[v]+w)
			{
				if(v!=s)ans[to]=min(ans[to],max(ans[v],v)); 
			}
		}
	}
} 
int main()
{ 
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d%d",&n,&m);
		init();
		res=0;
		while(m--)
		{
			scanf("%d%d%d",&u,&v,&w);
			add(u,v,w);add(v,u,w);
		}
		for(int i=1;i<=n;++i)
		{
			dijkstra(i);
			for(int j=1;j<=n;++j)
			res+=ans[j];
		}
		printf("%lldn",res%mod);
	}
	return 0;
}

C.hdu6715 算术(莫比乌斯反演)

题目

思路来源

https://www.cnblogs.com/cmyg/p/11405524.html

题解

寒假做过gcd的，暑假换成lcm就不会了……

现在觉得，推mobius的式子好有意思！

会了几个公式，很多时候，lcm要根据mu(k)不等于0，提一个mu(k)平方=1出来

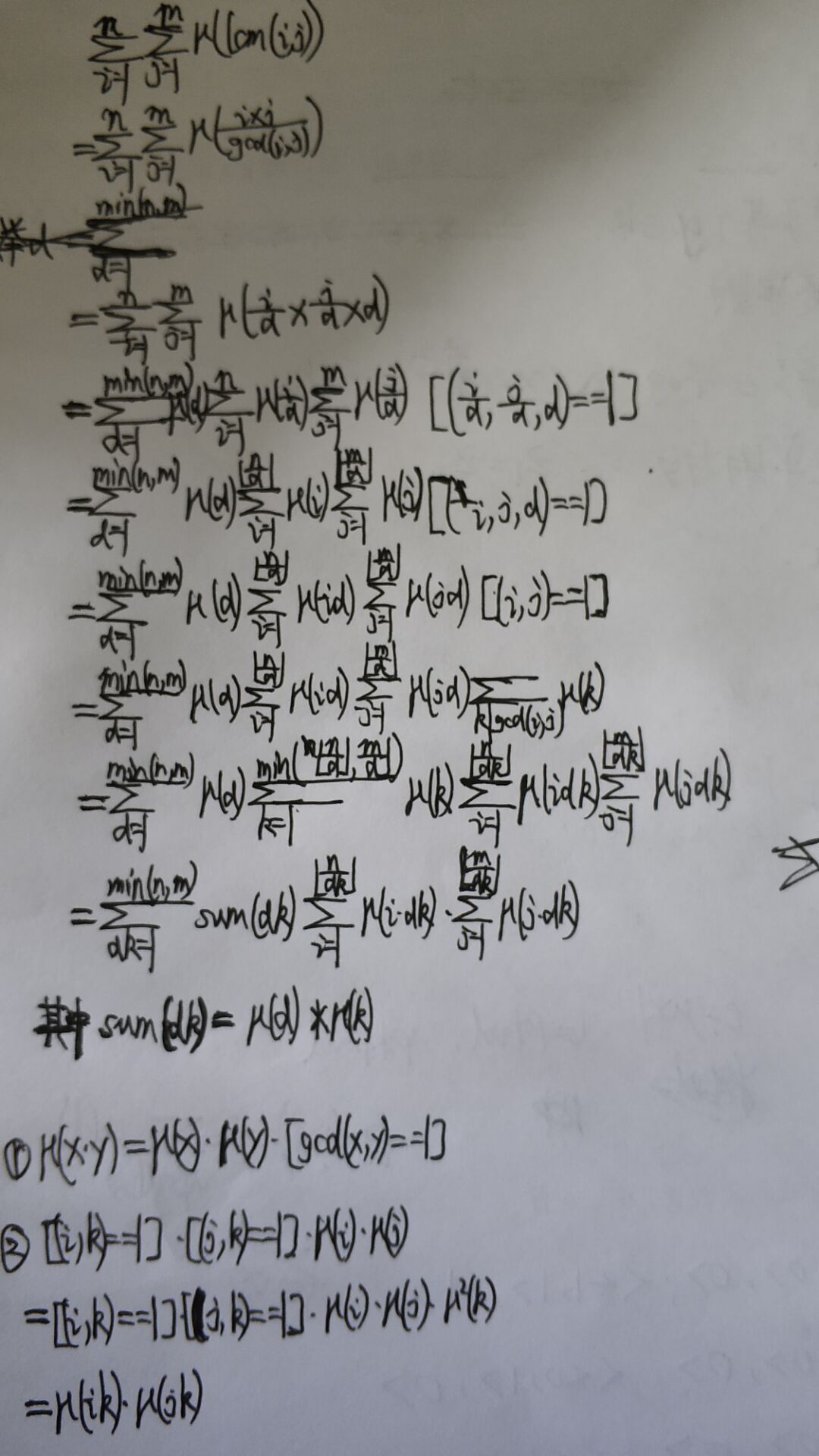
复杂度O(nlogn)

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
bool ok[maxn];
int prime[maxn],mu[maxn],cnt;
int T,n,m,mn;
ll sum[maxn],ans,ans1,ans2,ans3;
void sieve()
{
	mu[1]=1;
	for(ll i=2;i<maxn;++i)
	{
		if(!ok[i])
		{
			prime[cnt++]=i;
			mu[i]=-1;
		}
		for(int j=0;j<cnt;++j)
		{
			if(i*prime[j]>=maxn)break;
			ok[i*prime[j]]=1;
			if(i%prime[j]==0)
			{
				mu[i*prime[j]]=0;//如果开的是全局,就不用管 
				break; 
			}
			else mu[i*prime[j]]=-mu[i];
		}
	}
	for(int i=1;i<maxn;++i)//d
	{
		for(int j=i;j<maxn;j+=i)//d*k
		sum[j]+=mu[i]*mu[j/i];
	}	
}
int main()
{
	sieve();
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&n,&m);
		mn=min(n,m);
		ans=0;
		for(int i=1;i<=mn;++i)
		{
			ans1=sum[i];
			ans2=0;
			for(int j=i;j<=n;j+=i)
			ans2+=mu[j];
			ans3=0;
			for(int j=i;j<=m;j+=i)
			ans3+=mu[j];
			ans+=ans1*ans2*ans3;
		}
		printf("%lldn",ans);
	} 
	return 0;
}

最后

以上就是无奈钢笔为你收集整理的2019 百度之星初赛三 补题的全部内容，希望文章能够帮你解决2019 百度之星初赛三 补题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。