我是靠谱客的博主 甜蜜八宝粥，最近开发中收集的这篇文章主要介绍SDU程序设计思维Week14 矩阵快速幂优化DPSDU程序设计思维Week14 矩阵快速幂优化DP，觉得挺不错的，现在分享给大家，希望可以做个参考。
概述
SDU程序设计思维Week14 矩阵快速幂优化DP
A - Q老师与石头剪刀布
Description
每一个大人曾经都是一个小孩，Q老师 也一样。
为了回忆童年，Q老师 和 Monika 玩起了石头剪刀布的游戏，游戏一共 n 轮。无所不知的 Q老师 知道每一轮 Monika 的出招，然而作为限制， Q老师 在这 n 轮游戏中必须恰好出 a 次石头，b 次布和 c 次剪刀。
如果 Q老师 赢了 Monika n/2(上取整) 次，那么 Q老师就赢得了这场游戏，否则 Q老师 就输啦！
Q老师非常想赢，他想知道能否可以赢得这场游戏，如果可以的话，Q老师希望你能告诉他一种可以赢的出招顺序，任意一种都可以。
第一行一个整数 t(1 ≤ t ≤ 100)表示测试数据组数。然后接下来的 t 组数据，每一组都有三个整数：
第一行一个整数 n(1 ≤ n ≤ 100)
第二行包含三个整数 a, b, c(0 ≤ a, b, c ≤ n)。保证 a+b+c=n
第三行包含一个长度为 n 的字符串 s，字符串 s 由且仅由 'R', 'P', 'S' 这三个字母组成。第 i 个字母 s[i] 表示 Monika 在第 i 轮的出招。字母 'R' 表示石头，字母 'P' 表示布，字母 'S' 表示剪刀
对于每组数据：
如果 Q老师 不能赢，则在第一行输出 "NO"(不含引号)
否则在第一行输出 "YES"(不含引号)，在第二行输出 Q老师 的出招序列 t。要求 t 的长度为 n 且仅由 'R', 'P', 'S' 这三个字母构成。t 中需要正好包含 a 个 'R'，b 个 'P' 和 c 个 'S'
"YES"/"NO"是大小写不敏感的，但是 'R', 'P', 'S' 是大小写敏感的。
Sample
Input:
2
3
1 1 1
RPS
3
3 0 0
RPS
Output:
YES
PSR
NO
Idea
题意：石头剪刀布，求Q老师赢的次数，能不能超过1/2
记录每局Q老师的出招，根据石头剪刀布的胜负关系，首先尽可能得让Q赢，将有限次的石头剪刀布分配到Q可以赢的局，剩下的石头剪刀布随机分配。最后判断赢的次数是否超过1/2
Summary
这题和上周的石头剪刀布类似，根据胜负关系先尽可能让Q赢，由于只需要求出赢的次数，所以剩余的几次石头剪刀布随机分配即可
Codes
#include <iostream>
#include <cmath>
#include <string>
using namespace std;
int T, n, a, b, c;
string s;
char ans[120];
int main()
{
cin >> T;
while (T--)
{
cin >> n;
cin >> a >> b >> c;
cin >> s;
for (int i = 1; i <= n; i++)
ans[i] = '1';
int num = 0;
for (int i = 1; i <= n; i++) {
if (s[i - 1] == 'R'&&b > 0)b--, num++, ans[i]= 'P';
else if (s[i - 1] == 'P'&&c > 0)c--, num++, ans[i]= 'S';
else if (s[i - 1] == 'S'&&a > 0)a--, num++, ans[i]= 'R';
}
for (int i = 1; i <= n; i++) {
if (ans[i] == '1') {
if (a > 0)ans[i] = 'R', a--;
else if (b > 0)ans[i] = 'P', b--;
else if (c > 0)ans[i] = 'S', c--;
}
}
if (num >= ceil((float)n / 2.0)) {
printf("YESn");
for (int i = 1; i <= n; i++)
printf("%c", ans[i]);
printf("n");
}
else printf("NOn");
}
}
B - Q老师与十字叉
Description
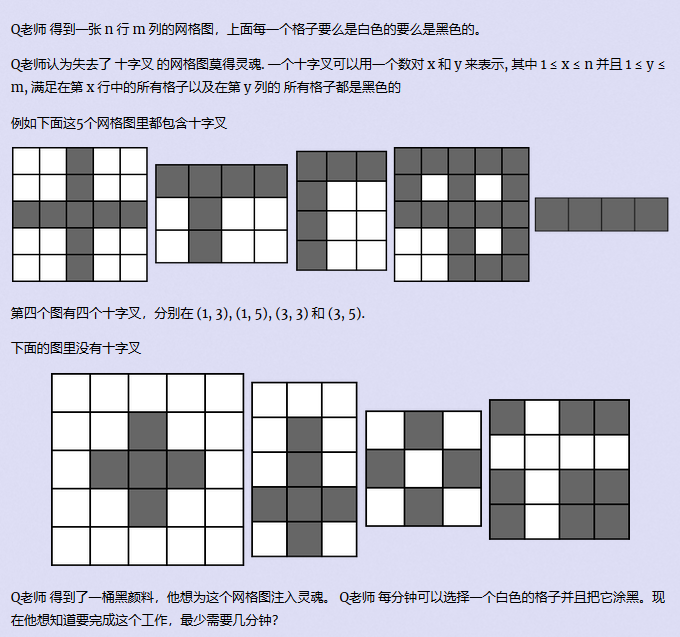
Sample
Input:
9
5 5
..*..
..*..
*****
..*..
..*..
3 4
****
.*..
.*..
4 3
***
*..
*..
*..
5 5
*****
*.*.*
*****
..*.*
..***
1 4
****
5 5
.....
..*..
.***.
..*..
.....
5 3
...
.*.
.*.
***
.*.
3 3
.*.
*.*
.*.
4 4
*.**
....
*.**
*.**
Output:
0
0
0
0
0
4
1
1
2
Idea
题意：求最少涂黑几个白色格子可以使网格图有十字叉
- 记录行列格子的颜色，并记录各行各列黑格子的数量
- 遍历每个格子，计算当前格子所在行所在列共有几个白格子
如果为0，即已有十字叉，无需涂格子
当前格子属于行列交叉处，如果该格子为白色，则只需涂一次该格子，所以总数要减一
答案取最小值
Summary
这题注意数据范围，行列都是<50000，二维数组不能开这么大，所以要利用vector
Codes
#include <iostream>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
int T, n, m;
vector<char> s[50020];
int hang[50020], lie[50020];
int main()
{
cin >> T;
while (T--)
{
cin >> n >> m;
for (int i = 0; i < n; i++)
{
hang[i] = 0;
s[i].clear();
}
for (int j = 0; j < m; j++)
lie[j] = 0;
int ans = INT_MAX;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
{
char c;
cin >> c;
s[i].push_back(c);
if (s[i][j] == '*') {
hang[i]++;
lie[j]++;
}
}
int num ;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++) {
num = n + m - (hang[i] + lie[j]);
if (num == 0) { ans = 0; break; }
if (s[i][j] == '.')num--;
ans = min(ans, num);
}
cout << ans << endl;
}
}
C - Q老师的考验
Description
Q老师 对数列有一种非同一般的热爱，尤其是优美的斐波那契数列。
这一天，Q老师 为了增强大家对于斐波那契数列的理解，决定在斐波那契的基础上创建一个新的数列 f(x) 来考一考大家。数列 f(x) 定义如下：
当 x < 10 时，f(x) = x；
当 x ≥ 10 时，f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10)，ai 只能为 0 或 1。
Q老师 将给定 a0～a9，以及两个正整数 k m，询问 f(k) % m 的数值大小。
聪明的你能通过 Q老师 的考验吗？
输出文件包含多组测试用例，每组测试用例格式如下：
第一行给定两个正整数 k m。（k < 2e9, m < 1e5）
第二行给定十个整数，分别表示 a0～a9。
对于每一组测试用例输出一行，表示 f(k) % m 的数值大小。
Sample
Input:
10 9999
1 1 1 1 1 1 1 1 1 1
20 500
1 0 1 0 1 0 1 0 1 0
Output:
45
104
Idea
- Matrix结构体，重载乘法运算符
- 构造10x10转移矩阵，矩阵的幂次是k-9
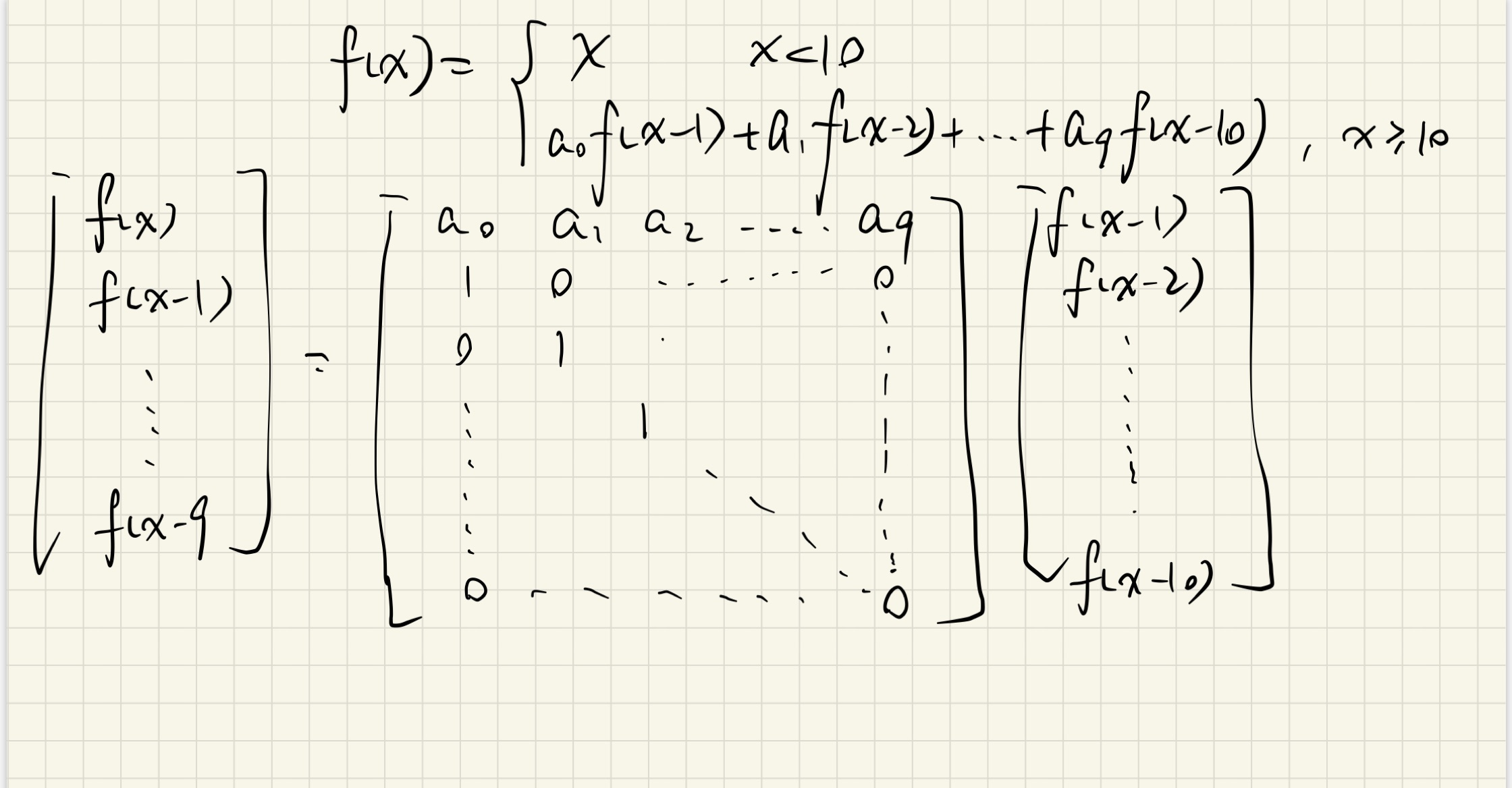
- 矩阵快速幂求解求模后的答案
Summary
这题是利用矩阵快速幂求解线性递推，关键在于构造10x10的转移矩阵。
Codes
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
long long k, m;
int a[12];
const int N = 10;
struct Matrix {
long long a[N][N];
Matrix operator*(const Matrix& t)const {
Matrix ret;
for(int i=0;i<N;++i)
for (int j = 0; j < N; ++j) {
for (int k = 0; k < N; ++k) {
ret.a[i][j] += a[i][k] * t.a[k][j] % m;
ret.a[i][j] %= m;
}
}
return ret;
}
Matrix() { memset(a, 0, sizeof(a)); }
Matrix(const Matrix& t) { memcpy(a, t.a, sizeof(a)); }
};
void solve(Matrix a,int x)
{
Matrix ret;
for (int i = 0; i < 10; i++)
ret.a[i][i] = 1;
while (x) {
if (x & 1)ret = ret * a;
a = a * a;
x >>= 1;
}
long long ans = 0;
for (int i = 0; i < 10; ++i)
ans += ret.a[0][i] * (9 - i) % m;
cout << ans % m << endl;
}
int main()
{
while (scanf("%lld%lld",&k,&m)!=EOF)
{
Matrix x;
memset(x.a, 0, sizeof(x.a));
if (k < 10) {
cout << k % m << endl;
continue;
}
for (int i = 0; i < 10; i++)
cin >> a[i];
for (int i = 0; i < 10; ++i)
x.a[0][i] = a[i];
for (int i = 1; i < 10; ++i)
x.a[i][i - 1] = 1;
solve(x, k - 9);
}
}
D - Q老师染砖
Description
衣食无忧的 Q老师 有一天突发奇想，想要去感受一下劳动人民的艰苦生活。
具体工作是这样的，有 N 块砖排成一排染色，每一块砖需要涂上红、蓝、绿、黄这 4 种颜色中的其中 1 种。且当这 N 块砖中红色和绿色的块数均为偶数时，染色效果最佳。
为了使工作效率更高，Q老师 想要知道一共有多少种方案可以使染色效果最佳，你能帮帮他吗？
第一行为 T，代表数据组数。(1 ≤ T ≤ 100)
接下来 T 行每行包括一个数字 N，代表有 N 块砖。(1 ≤ N ≤ 1e9)
输出满足条件的方案数，答案模 10007。
Sample
Input:
2
1
2
Output:
2
6
Idea
- DP状态
A[i]表示i个格子，红绿均为偶数的染色方案数
B[i]表示i个格子，红绿均为奇数的染色方案数
C[i]表示i个格子，红绿有一个为偶数的染色方案数 - 状态转移，转移矩阵是3x3，幂次是n
- 利用与C题类似的结构解题，最终答案%10007
Summary
这题与C题方法相似，本质上还是线性递推，关键在于确定转移矩阵
Codes
#include <iostream>
using namespace std;
int T,n;
const int N = 3;
struct Matrix {
long long a[N][N];
Matrix operator*(const Matrix& t)const {
Matrix ret;
for (int i = 0; i < N; ++i)
for (int j = 0; j < N; ++j) {
for (int k = 0; k < N; ++k) {
ret.a[i][j] += a[i][k] * t.a[k][j] % 10007;
ret.a[i][j] %= 10007;
}
}
return ret;
}
Matrix() { memset(a, 0, sizeof(a)); }
Matrix(const Matrix& t) { memcpy(a, t.a, sizeof(a)); }
};
void solve(Matrix x, int n) {
Matrix ans;
for (int i = 0; i < N; i++)
ans.a[i][i] = 1;
while (n) {
if (n & 1)ans = ans * x;
x = x * x;
n >>= 1;
}
long long res = 0;
res = ans.a[0][0] % 10007;
printf("%lldn", res);
}
int main()
{
cin >> T;
while (T--) {
cin >> n;
Matrix x;
x.a[0][0] = x.a[1][1] = x.a[2][0] = x.a[2][1] = x.a[2][2] = 2;
x.a[0][2] = x.a[1][2] = 1;
solve(x, n);
}
}
E - Q老师度假
Description
忙碌了一个学期的 Q老师 决定奖励自己 N 天假期。
假期中不同的穿衣方式会有不同的快乐值。
已知 Q老师 一共有 M 件衬衫，且如果昨天穿的是衬衫 A，今天穿的是衬衫 B，则 Q老师 今天可以获得 f[A][B] 快乐值。
在 N 天假期结束后，Q老师 最多可以获得多少快乐值？
输入文件包含多组测试样例，每组测试样例格式描述如下：
第一行给出两个整数 N M，分别代表假期长度与 Q老师 的衬衫总数。（2 ≤ N ≤ 100000, 1 ≤ M ≤ 100）
接下来 M 行，每行给出 M 个整数，其中第 i 行的第 j 个整数，表示 f[i][j]。（1 ≤ f[i][j] ≤ 1000000）
测试样例组数不会超过 10。
每组测试样例输出一行，表示 Q老师 可以获得的最大快乐值。
Sample
Input:
3 2
0 1
1 0
4 3
1 2 3
1 2 3
1 2 3
Output:
2
9
Idea
- 获取快乐值f[i][j],表示昨天穿了i，今天穿了j
- 定义状态dp[i][j]表示第i天穿的衣服为j所获得的快乐值总和
状态转移方程：dp[i][j]=max(dp[i-1][k]+f[k][j])
利用矩阵快速幂优化：
转移矩阵如上，是MxM矩阵，幂次是n-1 - 利用与之前题目相似的结构求得最终答案矩阵，取矩阵中最大元素值
Summary
这题利用矩阵快速幂优化DP将时间复杂度降至O(M*M)，转移矩阵是快乐值矩阵的转置。
总结：矩阵快速幂可优化min、max、加减乘除的递推式
Codes
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
long long n, m;
long long N ;
long long f[120][120];
struct Matrix {
long long a[120][120];
Matrix operator*(const Matrix& t)const {
Matrix ret;
for (int i = 0; i < N; ++i)
for (int j = 0; j < N; ++j) {
for (int k = 0; k < N; ++k) {
ret.a[i][j] = max(ret.a[i][j], a[i][k] + t.a[k][j]);
}
}
return ret;
}
Matrix() { memset(a, 0, sizeof(a)); }
Matrix(const Matrix& t) { memcpy(a, t.a, sizeof(a)); }
};
void solve(Matrix x, int n) {
Matrix ans;
while (n) {
if (n & 1)ans = ans * x;
x = x * x;
n >>= 1;
}
long long res = 0;
for (int i = 0; i < m; i++)
for (int j = 0; j < m; j++)
res = max(res, ans.a[i][j]);
printf("%lldn", res);
}
int main()
{
while(scanf("%d%d",&n,&m)!=EOF){
N = m;
for (int i = 0; i < m; i++)
for (int j = 0; j < m; j++)
cin >> f[i][j];
Matrix x;
for (int i = 0; i < m; i++)
for (int j = 0; j < m; j++)
x.a[i][j] = f[j][i];
solve(x, n-1);
}
}
最后
以上就是甜蜜八宝粥为你收集整理的SDU程序设计思维Week14 矩阵快速幂优化DPSDU程序设计思维Week14 矩阵快速幂优化DP的全部内容，希望文章能够帮你解决SDU程序设计思维Week14 矩阵快速幂优化DPSDU程序设计思维Week14 矩阵快速幂优化DP所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复