我是靠谱客的博主 高贵大白，这篇文章主要介绍数据结构与算法——高级数据结构：字典树/Trie树+线段树+树状数组1. 字典树/Trie Tree2. 线段树/Segment Tree3. 树状数组，现在分享给大家，希望可以做个参考。
文章目录
- 1. 字典树/Trie Tree
- 1.1 场景
- 1.2 思路
- 1.3 代码
- 2. 线段树/Segment Tree
- 2.1 场景
- 2.2 思路
- 2.3 代码
- 3. 树状数组
1. 字典树/Trie Tree
1.1 场景
- 在海量字符串中做查询操作（但不局限于字符串问题）
- 节约空间：10万个只包含小写字母的字符串，采用字典树可以减少内存消耗
- 节约时间：检索效率高
- 扩展：
- 对数字的二进制01串构造字典树可以快速按位查询数字是否存在
- 利用KMP的利用失配信息思想快速继续匹配，可以实现AC自动机算法
- 对构造好的字典树进行BFS预处理并增加直达叶子节点的指针时，可以解决输入最小操作数的问题
1.2 思路
-
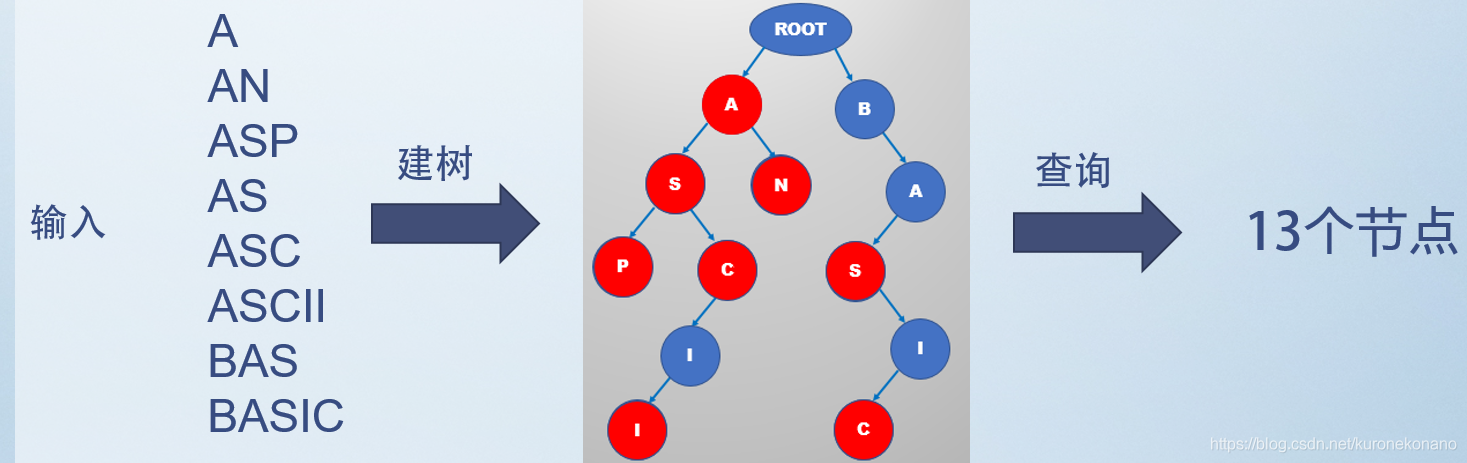
根节点不包含字符，每条边代表一个字符
-
从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串
-
每个节点的所有子节点包含的字符都不相同
参考链接：https://blog.csdn.net/kuronekonano/article/details/100063157
1.3 代码
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80class TrieNode { char val; // 当前节点存储的字符 TrieNode[] next = new TrieNode[26]; // 节点下的孩子数组，通常为26个字母 boolean isEnd = false; // 标记是否为待存储的最后一个字符，下面没有子节点 public TrieNode() { } public TrieNode(char val) { this.val = val; } } class Trie { TrieNode root; public Trie() { root = new TrieNode(); root.val = ' '; } // 1.插入一个单词到Trie树中 public void insert(String word) { TrieNode cur_node = root; char[] chars = word.toCharArray(); int len = chars.length; for (int i = 0; i < len; i ++) { char c = chars[i]; if (cur_node.next[c - 'a'] == null) { cur_node.next[c - 'a'] = new TrieNode(c); } cur_node = cur_node.next[c - 'a']; } cur_node.isEnd = true; } // 2.判断某个单词是否在Trie树之中 public boolean get(String word) { TrieNode cur_node = root; char[] chars = word.toCharArray(); int len = chars.length; for (int i = 0; i < len; i ++) { char c = chars[i]; // 在单词还未走完的时候发现已经不匹配了 if (cur_node.next[c - 'a'] == null) { return false; } cur_node = cur_node.next[c - 'a']; } // 如果后面还有，说明未储存word return cur_node.isEnd; } // 3.判断当前的单词是否为Trie树某个单词的前缀 public boolean isPrefix(String word) { TrieNode cur_node = root; char[] chars = word.toCharArray(); int len = chars.length; for (int i = 0; i < len; i ++) { char c = chars[i]; // 在单词还未走完的时候发现已经不匹配了 if (cur_node.next[c - 'a'] == null) { return false; } cur_node = cur_node.next[c - 'a']; } return true; } } public class Test { public static void main(String[] args) { Trie trie = new Trie(); trie.insert("abcdefg"); trie.insert("abomn"); trie.insert("acg"); trie.insert("dkz"); System.out.println(trie.get("abcdefg")); // true System.out.println(trie.isPrefix("abc")); // true } }
2. 线段树/Segment Tree
2.1 场景
复制代码
1
2给定一个数组，随机截取一段，计算区间和；随机修改数组中的元素。假设数组很大，截取或者修改的操作很频繁
2.2 思路
复制代码
1
2
31.通过遍历对区间内数字进行累加：O(N)，修改：O(1) 2.使用前缀和，先计算出前缀和，利用前缀和计算区间和：O(1)，修改：O(N)
如何平衡计算区间和、修改的时间复杂度？使用线段树！
构造线段树：根节点包含整个区间，然后依此对区间二分，构造新节点
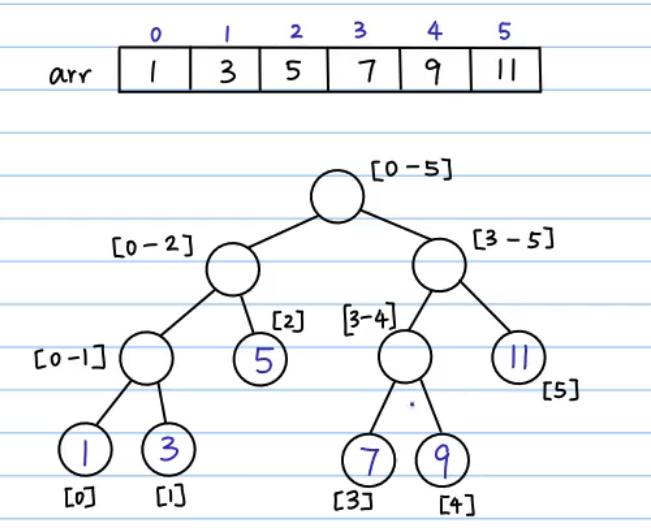
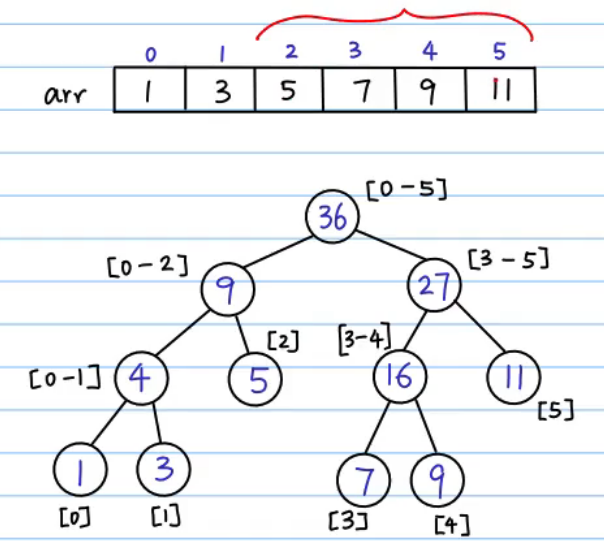
依据填入的叶子节点数据构造完整的线段树：
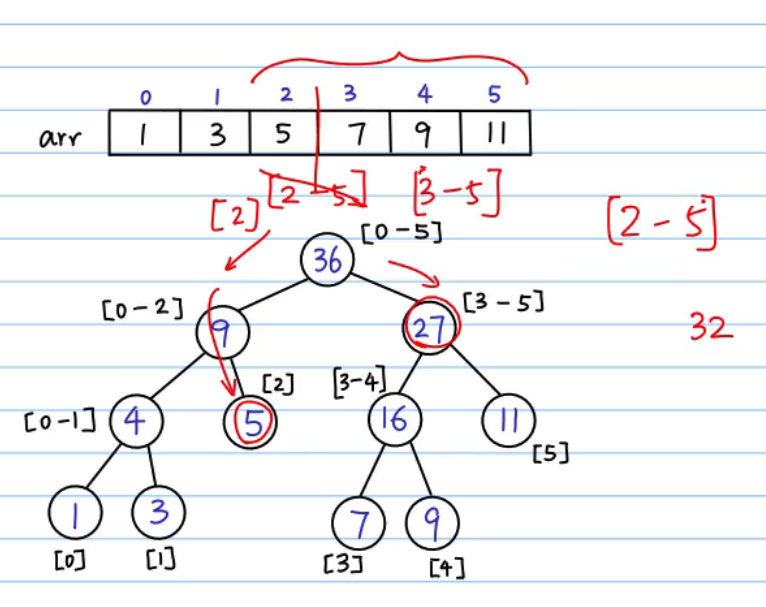
计算[2,5]区间和：在根节点处分割区间为[2],[3,5]，从左子树找到区间[2]的元素，右子树根节点即[3,5]，最后得出区间和：32=5+27
修改索引为4的元素为6：
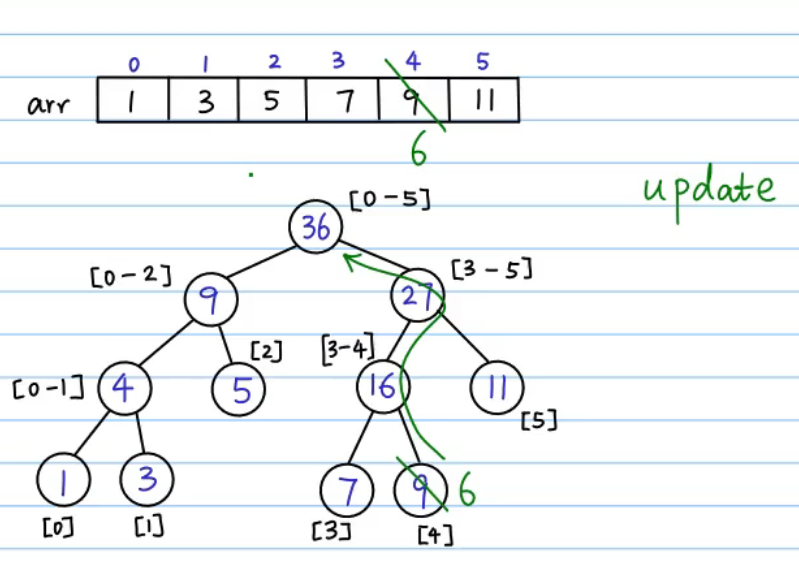
将线段树转换成满二叉树，对中间的叶子节点建立虚节点：
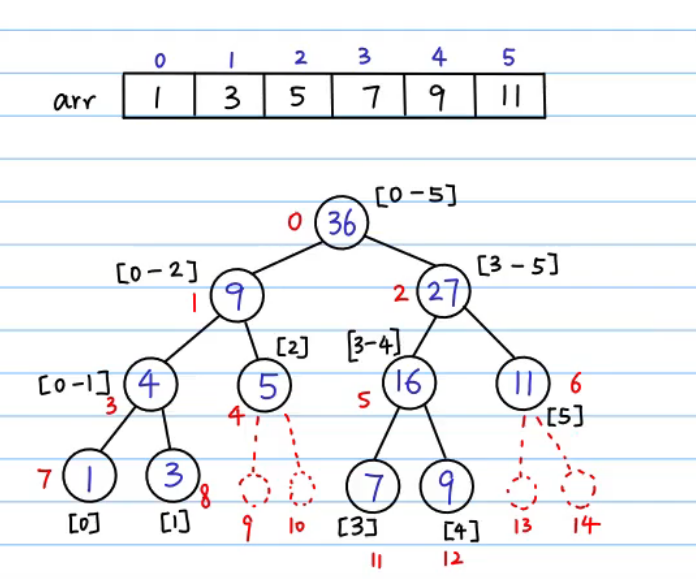
将线段树转成数组：（注意满二叉树节点编号的性值）
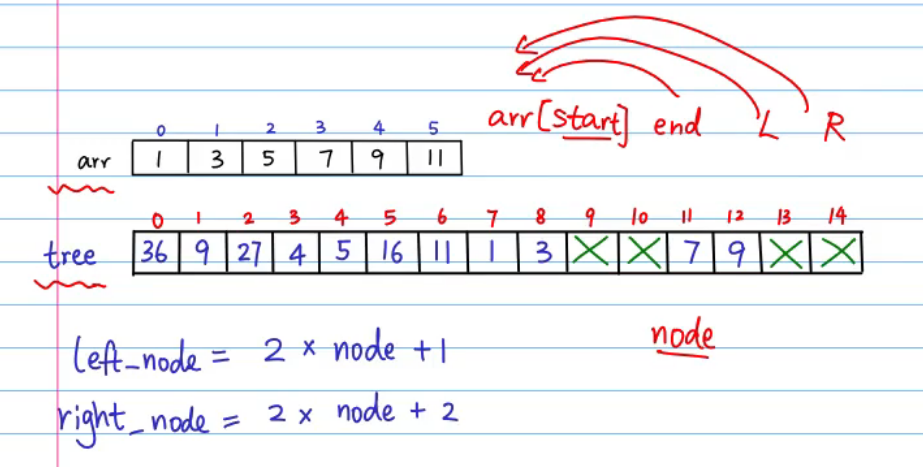
2.3 代码
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103import java.util.Arrays; public class SegmentTree { private static final int MAX_LEN=20; public static void main(String[] args) { int[] arr=new int[] {1,3,5,7,9,11}; int[] tree=new int[MAX_LEN]; build_tree(arr,tree,0,0,arr.length-1);//node=0,start=0,end=5 //[36, 9, 27, 4, 5, 16, 11, 1, 3, 0, 0, 7, 9, 0, 0, 0, 0, 0, 0, 0] System.out.println(Arrays.toString(tree)); //[33, 9, 24, 4, 5, 13, 11, 1, 3, 0, 0, 7, 6, 0, 0, 0, 0, 0, 0, 0] update_tree(arr, tree, 0, 0, arr.length-1, 4, 6); System.out.println(Arrays.toString(tree)); //29 int res=query_tree(arr, tree, 0, 0, arr.length-1, 2, 5); System.out.println(res); } /** * 1.对初始数组arr[]的start-end的区间构造tree[] * @param node tree[]根节点 * @param start arr[]左边界 * @param end arr[]右边界 */ public static void build_tree(int[] arr,int[] tree,int node,int start,int end) { //设置递归出口 if(start==end) { tree[node]=arr[start]; return; } int mid=(start+end)/2;//mid=(0+5)/2=2 int left_node=node*2+1;//left=1 int right_node=node*2+2;//right=2 build_tree(arr,tree,left_node,start,mid); build_tree(arr,tree,right_node,mid+1,end); tree[node]=tree[left_node]+tree[right_node]; } /** * 2.修改初始数组arr[]的idx位置的元素为val */ public static void update_tree(int[] arr,int[] tree,int node,int start,int end,int idx,int val) { //设置递归出口 if(start==end) { arr[idx]=val; tree[node]=val; return; } int mid=(start+end)/2; int left_node=node*2+1; int right_node=node*2+2; //改左子树 if(idx>=start && idx<=mid) { update_tree(arr, tree, left_node, start, mid, idx, val); } //改右子树 else { update_tree(arr, tree, right_node, mid+1, end, idx, val); } tree[node]=tree[left_node]+tree[right_node]; } /** * 3.计算初始数组arr[]的[L,R]的区间和 */ public static int query_tree(int[] arr,int[] tree,int node,int start,int end,int L,int R) { //设置递归出口 if(R<start || end<L) { return 0; } if(start==end) { return tree[node]; } if(L<=start && end<=R) { return tree[node]; } int mid=(start+end)/2; int left_node=node*2+1; int right_node=node*2+2; int sum_left=query_tree(arr, tree, left_node, start, mid, L, R); int sum_right=query_tree(arr, tree, right_node, mid+1, end, L, R); return sum_left+sum_right; } }
完整教程：
bilibili - 正月点灯笼 - 【数据结构】线段树（Segment Tree）
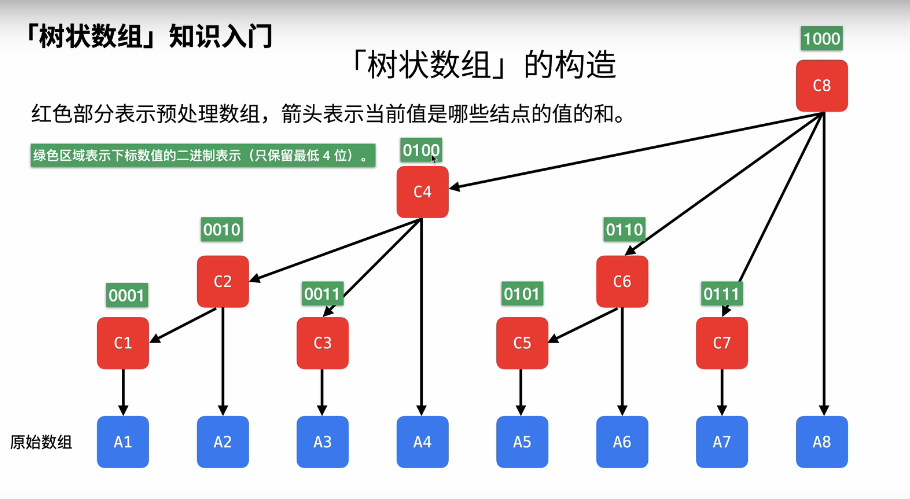
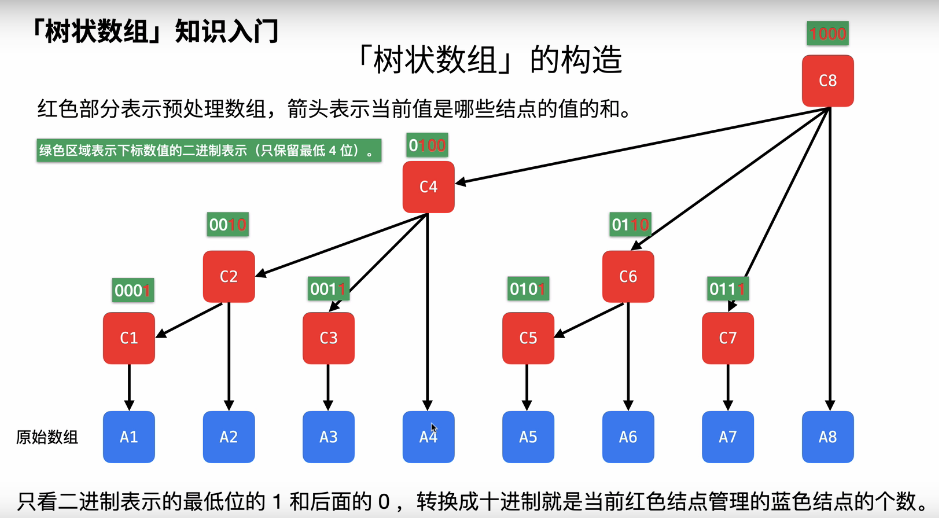
3. 树状数组
高效计算数组的前缀和、区间和以及解决单点更新问题
不能解决数组有增加或修改的情况
它可以以O(logn) 的时间得到任意前缀和，并同时支持在O(logn) 时间内支持动态单点值的修改
空间复杂度O(n)
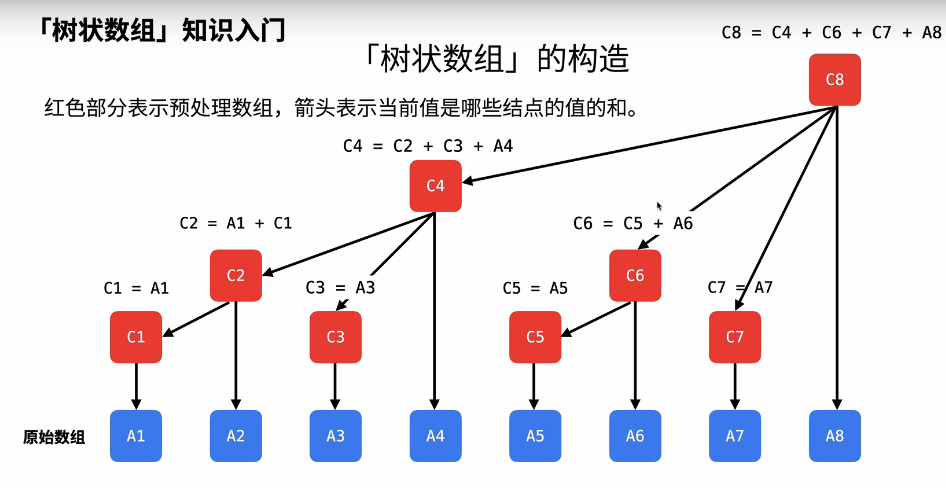
例题：
LeetCode 315. 计算右侧小于当前元素的个数
给定一个整数数组 nums，按要求返回一个新数组 counts。数组 counts 有该性质： counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
复制代码
1
2
3
4
5
6
7
8输入：nums = [5,2,6,1] 输出：[2,1,1,0] 解释： 5 的右侧有 2 个更小的元素 (2 和 1) 2 的右侧仅有 1 个更小的元素 (1) 6 的右侧有 1 个更小的元素 (1) 1 的右侧有 0 个更小的元素
完整教程：
bilibili - liweiwei1419 -「树状数组」知识入门（「力扣」第 315 题）
最后
以上就是高贵大白最近收集整理的关于数据结构与算法——高级数据结构：字典树/Trie树+线段树+树状数组1. 字典树/Trie Tree2. 线段树/Segment Tree3. 树状数组的全部内容，更多相关数据结构与算法——高级数据结构：字典树/Trie树+线段树+树状数组1.内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复