目录

1. 栈相关（stack）

例1. 最小栈

例2. 用栈实现队列

2. 单调栈

例3. 直方图最大矩形面积 （单调递增栈）

例4. 最大树 (MaxTree)（单调递减栈）

例5. 接雨水 （单调递减栈）

3. 哈希表(or 散列表) （hash table）

例6. 实现一个字符串转数字的常用hash函数 （magic number 33）

例7. 重哈希（Rehashing）

例8. LRU Cache (Least Recently Used 最近最少使用缓冲器）

例9. 乱序字符串分组（anagrams）

例10. 无序整数数组中 最长连续子序列

4. 堆 （heap）

例11. 寻找数据流的中位数

例12. 堆化操作 siftdown

例13. 找从小到大的第n个丑数

1. 栈相关（stack）

例1. 最小栈

描述：实现一个栈, 支持以下操作:push(val) 将 val 压入栈;pop() 将栈顶元素弹出, 并返回这个弹出的元素;min() 返回栈中元素的最小值;要求 O(1) 开销;保证栈中没有数字时不会调用 min(). （来源 ：lintcode 12 · 带最小值操作的栈 = leetcode 剑指 Offer 30. 包含min函数的栈 = leetcode 155. 最小栈）
样例
输入：push(1)  min()  push(2)  min()  push(3)  min()
输出：                  1                     1                      1

代码1_常规方法

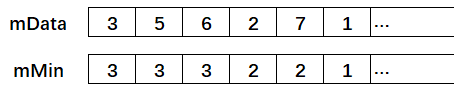
因为每层都有返回当前情况下的最小值，所以每次存储一个值，就需要更新（或者确认）当前最小栈的最小值。所以考虑使用两个普通栈（std::stack）来实现。一个stack<int> mData 存储数据，一个stack<int> mMin 存储当前状态下的最小值。在push入栈时，比较当前值和当前最小值那个更小，若当前值更小，则将当前值加入mMin 栈，否则，将当前最小值再次加入 mMin 栈 （可改进点）。以便在pop时，mData每弹出一个元素, mMin就弹出一个元素。代码实现如下。

class MinStack {
public:
    stack<int> mData;
    stack<int> mMin; 
    
    MinStack(){ }

    void push(int number) {
        mData.push(number);
        if (mMin.empty()) {
            mMin.push(number);
        } else {
            mMin.push(std::min(number, mMin.top()));
        }
    }

    int pop() {
        if (!mData.empty()) {
            int res = mData.top();
            mData.pop();
            mMin.pop();
            return res;
        } else {
            return INT_MIN;
        }
    }

    int min() {
        return mMin.top();
    }
};

代码1_空间优化（重点记忆）

可以看到上述 mMin栈 中 有很多重复的元素，若第一个值是1，后面全是比1大的n个数，则mMin中岂不是要存n个1，存一个1，省点空间不可以吗？答案是可以的。此时的方法变成了，在push时，只有在当前值 <= 当前最小值时，才将 当前值 插入 mMin栈中，否则不必插入。特别注意，此时在pop()元素时，只有mData栈中的栈顶元素 等于 mMin的栈顶元素时，才弹出 mMin的栈顶元素（即最小值），否则mMin栈也不必弹出。

class MinStack {
public:
    stack<int> mData;
    stack<int> mMin; 
    
    MinStack(){ }

    void push(int number) {
        mData.push(number);
        if (mMin.empty()) {
            mMin.push(number);
        } else if (number <= mMin.top()) { //只有当 当前值 小于mMin栈顶元素 (最小值)时，才加入 mMin栈中
            mMin.push(number);
        }
    }

    int pop() {
        if (!mData.empty()) {
            if (mData.top() == mMin.top()) { // 只有当两个栈顶元素相等时，mMin栈才弹出栈顶元素。
                mMin.pop();
            }
            int res = mData.top();
            mData.pop();
            return res;
        } else {
            return INT_MIN;
        }
    }

    int min() {
        return mMin.top();
    }
};

例2. 用栈实现队列

描述：正如标题所述，你只能使用两个栈来实现队列的一些操作。队列应支持 push(element)，pop() 和 top()，其中pop是弹出队列中的第一个(最前面的)元素。pop和top方法都应该返回第一个元素的值。假设调用pop()函数的时候，队列非空。（来源：lintcode 40 · 用栈实现队列 ≈ leetcode 225. 用队列实现栈 ≈ leetcode 剑指 Offer 09. 用两个栈实现队列）
样例
输入：队列操作 = push(1)    pop()    push(2)    push(3)   top()     pop()
输出：                                      1                                        2           2
解释：pop和top方法都应该返回第一个元素的值。

代码

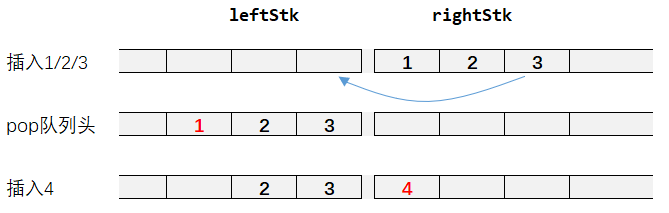
栈先进后出，队列先进先出。为了直观表示，我们定义2两栈， leftStk (用来取出元素) 和 rightStk（用来存放元素）, 所以，在pop时，需要把rightStk种的元素全部倒到 leftStk中，只要leftStk中还有元素，就从leftStk中取出，而rightStk主要用来存放元素。图示如下。

class MyQueue {
public:
    stack<int> leftStk;
    stack<int> rightStk;
    
    MyQueue() { }

    void push(int element) {
        rightStk.push(element);
    }

    int pop() {
        if (leftStk.empty()) {
            rightStk2RightStk(rightStk, leftStk);
        }
        int res = leftStk.top();
        leftStk.pop();
        return res;
    }

    int top() {
        if (leftStk.empty()) {
            rightStk2RightStk(rightStk, leftStk);
        }
        return leftStk.top();
    }

    void rightStk2RightStk (stack<int> & rightStk, stack<int> & leftStk) {
        while (!rightStk.empty()) {
            leftStk.push(rightStk.top()); //注意：这句话写的很简洁。
            rightStk.pop();
        }
    }
};

时间复杂度分析：虽然题中为了pop一个元素时，会进行 从 rightStk 到 leftStk 的n次（元素个数）遍历，但是这次整体遍历需要积攒n次，所以pop()的整体（平均）时间复杂度仍然还是O(1)。（分析时间复杂度，更多的是考虑每个元素进入数据结构 和 出数据结构 的次数。）

2. 单调栈

主要性质：（参考链接https://www.cnblogs.com/grandyang/p/8887985.html）

• 单调递增栈可以找到左起第一个比当前数字小的元素。例子：[2,1,5,6,2,3] ==》[2,1,5,6,2,3]
• 单调递减栈可以找到左起第一个比当前数字大的元素。例子：[2,5,6,0,3,1] ==》[2,5,6,0,3,1]

例3. 直方图最大矩形面积 （单调递增栈）

描述：给定非负整数数组 heights ，数组中的数字用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。（来源：leetcode 剑指 Offer II 039. 直方图最大矩形面积 = lintcode 122 · 直方图最大矩形覆盖 困难）

示例 : 输入：heights = [2,1,5,6,2,3]   输出：10

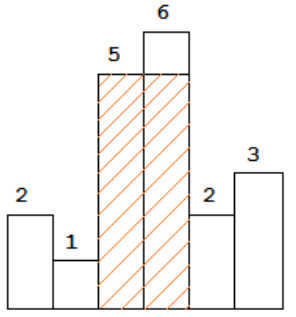
解释：最大的矩形为图中红色区域，面积为 10

代码

一种直观的想法是，对于当前位置 i, 找到左侧第一个比当前值小的位置的索引 leftIndex，再找到右侧比当前值小的索引 rightIndex, 然后当前位置对应的 矩形面积 = height[i] * (rightIndex - leftIndex - 1) 即可。然后在所有位置上取最大者。对于找 比当前位置小的 位置 ，使用单调栈（单调递增栈，单调递减栈）很方便解决该问题。同样使用找两侧的索引，来求面积的方法。

本文采用单调递增栈（从栈低到栈顶，数值依次变大）。则遍历到当前索引位置 i 时的 高度 cur = heights[i] 判断是否要插入栈：若 cur  比栈顶元素要 大，直接插入栈；若 cur  比栈顶元素要 小，则 依次弹出栈中 比 cur 大的元素。为了计算柱子的个数，代码采用在栈中插入索引的方式。在准备弹出时（下面代码while循环第一行），栈顶元素对应的柱子 （高度 = heights[stk.top()] ）即为当前所求对象，因为 当前遍历的柱子高度 cur <= 当前栈顶元素对应的高度，所以插入栈，这意味这 cur 对应的柱子 是 当前所求对象 的右边界，左边界为当前所求对象在单调递增栈中的前一个元素（因为是单调递增栈，所以 前一个元素 一定小于 当前所求对象 ）（即 stk.pop() 之后的 stk.top() ），所以 计算宽度 w = stk.empty() ? ( i - stk.top() - 1 ) : i;  当栈为空时，w = 当前索引 i 。

注意：这里为了计算每个位置对应的面积，需要最终将单调栈中的元素全部弹出，索引遍历范围是 [i, n] 。

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        if (n == 0) {
            return 0;
        }
        
        stack<int> stk;         // 采用单调递增栈 如 [1 5 6...
        int res = 0;
        for (int i = 0; i <= n; i++) {
            int cur = (i != n) ? heights[i] : -1; //为了将单调递增栈中的元素都pop出去，所以i最大需要到n, 同时 插入-1
            while (!stk.empty() && cur <= heights[stk.top()]) {  // 注意是 <= 小于等于就要弹出了。
                int h = heights[stk.top()];
                stk.pop();
                int w = !stk.empty() ? (i - stk.top() - 1) : i; // 这句话 重点理解：单调递减栈为空时，说明从尾到头都可算到最大矩形中。 // 当前 h 对应的高度下，左边界是h对应的索引的上一个(这里是 pop之后的 stk.top())， 右边界是 i, 两者之间的柱子的个数（可计算的最大间距值） 是 i - stk.top() - 1 
                res = max (res, h * w); 
            }
            stk.push(i);
        }

        return res;
    }
};

时间复杂度：O(n) 。把 O(n^2) 优化成 O(n) 的数据结构不多，单调栈就是其中一个。

另外 O(nlogn) 时间复杂度 的两种常见情况：

• 1. 排序，nlogn,  n * 二分法(logn)
• 2. 借助logn的数据结构：如 heap 如 priority_queue

例4. 最大树 (MaxTree)（单调递减栈）

描述：给出一个没有重复数字的整数数组，在此数组上建立最大树，其定义如下：根是数组中最大的数; 左子树和右子树元素分别是被父节点元素切分开的子数组中的最大值; 利用给定的数组构造最大树。（来源：lintcode 126 · 最大树 困难= leetcode 654. 最大二叉树 中等）
样例: 输入：A = [2, 5, 6, 0, 3, 1]   输出：{6,5,3,2,#,0,1}
解释：此数组构造的最大树是：

        6
       /
      5   3
     /     /
   2    0   1

代码

根据最大树的定义，最大值作为根节点，然后以最大值为分界线，左侧的作为左子树，右侧的作为右子树。在左子树上，最大的最为左子树的根节点..., 依次类推。考虑我们需要找到左侧第一个比当前值大的元素作为当前值的根节点，所以，这里 使用 vector 模拟一个 单调递减栈（如 2,5,6,0,3,1），当栈不为空时，若当前值 > 栈顶元素，则栈顶元素应该是当前元素的left 节点，若当前元素 < 栈顶元素，则当前元素应该是栈顶元素的right 节点。最终栈中剩余的元素是递减的，所以，栈底元素即为根节点（当然使用 stack<TreeNode*> stk 结构也是也可以的，只是最后要出栈到最后一个元素）。

注意：pop_back() 完后，要 判断“栈”是否为空 if (!stk.empty())  

/**
 * Definition of TreeNode:
 * class TreeNode {
 * public:
 *     int val;
 *     TreeNode *left, *right;
 *     TreeNode(int val) {
 *         this->val = val;
 *         this->left = this->right = NULL;
 *     }
 * }
 */
class Solution {
public:
    TreeNode * maxTree(vector<int> &A) {
        int n = A.size();
        if (n == 0) {
            return nullptr;
        }

        vector<TreeNode *> stk; //这里使用数组模拟单调递减栈[7, 5, 2 ...] //则最终的栈低元素(数组中的最大值)即为root节点
        
        for (int i = 0; i < n; i++) {
            TreeNode * curNode = new TreeNode(A[i]);
            while (!stk.empty() && A[i] > stk[stk.size()-1]->val) { //若当前值比 栈顶元素大，则栈顶元素为当前节点的左子节点(因为根据最大树的要求，在每一个子数组中，最大值左侧的数在左子树)
                curNode->left = stk[stk.size()-1];  // 谁大谁是“爸爸”
                stk.pop_back();
            }

            if (!stk.empty()) { //上面的处理完后，当遇到当前值小于此时的栈顶元素，则 当前值对应的节点，为栈顶元素节点的右子节点。
                stk[stk.size()-1]->right = curNode;  // 谁大谁是“爸爸”
            }

            stk.push_back(curNode);
        }

        return stk[0]; //注意：返回的是栈低节点(最大树，所以栈顶节点一定是最大的) //不是栈顶哦！！
    }
};

例5. 接雨水 （单调递减栈）

描述：给出 n 个非负整数，代表一张X轴上每个区域宽度为 1 的海拔图, 计算这个海拔图最多能接住多少（面积）雨水。（来源：lintcode 363 · 接雨水 中等 = leetcode 42. 接雨水 困难)42. 接雨水

样例1：
输入: [0,1,0]  输出: 0
样例2：
输入: [0,1,0,2,1,0,1,3,2,1,2,1]  输出: 6
挑战： O(n) 时间, O(1) 空间； O(n) 时间, O(n) 空间也可以接受

代码

该题后多种解法，这里以单调栈为例进行分析。考虑到计算当前位置上能接多少雨水，取决于左右两侧的最大值。所以选择使用单调递减栈 （因为可以方便找到比当前值大的元素，栈中元素从栈底到栈顶依次递减）。为了方便计算两个柱子之间的间距，同例4一样，我们在栈中保存高度数组对应的索引；同时，采用横向分层计算的方式比较方便。

我们依次将元素入栈，当遇到当前元素 i （记作 cur  = heights[i] ）比 栈顶元素对应的值 大时，就开始计算。 这里有三个关注的元素： 待判定是否插入栈的当前元素 cur （对应的索引设为 i）；栈顶元素 （对应的高度记为 bottom，此时必定是最低的一个）；栈顶元素的前一个元素（ 在进行一次 stk.pop()之后，索引成了 stk.top()）则 计算积水面积的 高度 h = min(heights[stk.top()], heights[i]) - bottom; （即当前计算对象，左右两侧的最小高度 减去 当前高度）。 宽度 w = i - stk.top() - 1; (即当前元素 对应的索引 i 减去 当前栈中（未弹出时）的倒数第二个索引 再减去 1)

注意：pop() 完后，要 判断栈是否为空 if (!stk.empty())  

class Solution {
public:
    int trapRainWater(vector<int> &heights) {
        // write your code here
        int n = heights.size();
        if (n <= 1) {
            return 0;
        }

        stack<int> stk; //为计算积水面积，左侧值比右侧大(构成"V"字型折现)才方便计算，所以采用单调递减栈[2,1,0...]
        int sum = 0;
        for (int i = 0; i < n; i++) {
            int cur = heights[i];    // 当前待判断是否入栈的元素 记作 cur
            while (!stk.empty() && cur >= heights[stk.top()]) {
                int bottom = heights[stk.top()]; //以当前栈顶元素作为计算对象,当前栈顶元素必定为此时的最低点
                stk.pop();                       // 在弹出后，若有计算记得判断栈是否为空！
                if (!stk.empty()) {
                    int h = min(heights[stk.top()], cur) - bottom;   //横向分层计算
                    int w = i - stk.top() - 1;
                    sum += h * w;
                }
            } 
            stk.push(i);
        }

        return sum;
    }
};

3. 哈希表(or 散列表) （hash table）

关于hash常问的问题有：（参考 C++_Hash容器总结）

• hash这种数据结构，你了解多少？内部怎么实现的？时间复杂度是什么样的？hash为什么是O(1) 插入删除查找的？什么情况下不能当成是O(1)的？
  • 我们知道，数据结构的物理存储结构只有两种：顺序存储结构和链式存储结构（像栈，队列，树，图等是从逻辑结构去抽象的，映射到内存中，也这两种物理组织形式），而在数组中根据下标查找某个元素，一次定位就可以达到，哈希表利用了这种特性，哈希表的主干就是数组。
• 你能不能自己实现一个hash map？hash function 怎么写的？
• hash常遇到的问题是什么？怎么解决 hash collision（哈希冲突）的？

例6. 实现一个字符串转数字的常用hash函数 （magic number 33）

​描述：在数据结构中，哈希函数是用来将一个字符串（或任何其他类型）转化为小于哈希表大小且大于等于零的整数。一个好的哈希函数可以尽可能少地产生冲突。一种广泛使用的哈希函数算法是使用数值 33，假设任何字符串都是基于 33 的一个大整数，比如：

 其中HASH_SIZE表示哈希表的大小(可以假设一个哈希表就是一个索引 00 ~ HASH_SIZE - 1的数组)。给出一个字符串作为 key 和一个哈希表的大小，返回这个字符串的哈希值。

对于这个问题你不需要自己设计hash算法，你只需要实现上述描述的hash算法即可。对于这个问题，您没有必要设计自己的哈希算法或考虑任何冲突问题，您只需要按照描述实现算法.（来源： lintcode 128 · 哈希函数 简单）

样例
输入:  key = "abcd", size = 1000   输出: 978    
样例解释：(97 * 33^3 + 98*33^2 + 99*33 + 100*1)%1000 = 978

代码

利用性质 ： 对一个数多次取余等于一次取余。 a%b%b = a%b。 注意：这里 33乘在sum上，然后下一次循环再乘在sum上，避免多次求33的n次方。

class Solution {
public:
    int hashCode(string &key, int HASH_SIZE) {
        int sum = 0;

        for (int i = 0; i < key.size(); i++) {
            sum = sum * 33 + (int)key[i];   // 注意：这里对 sum 乘以 33，避免了重复计算33的倍数
            sum %= HASH_SIZE;               // 利用性质 a%b%b = a%b
        }

        return sum;
    }
};

例7. 重哈希（Rehashing）

class Solution {
public:
    vector<ListNode*> rehashing(vector<ListNode*> hashTable) {
        int n = hashTable.size();
        if (n == 0) {
            return hashTable;
        }
        
        int N = 2 * n;
        vector<ListNode*> result(N, nullptr); //注意：直接初始化为 nullptr!(后面用来判断该位置是否有元素)
        for (int i = 0; i < n; i++) {      // 进入到处理原始hash中单个节点的逻辑
            ListNode * head = hashTable[i];  // 原始hash中的节点的头
            while (head != nullptr) {
                ListNode * nextNode = head->next;   //将 head 作为当前处理对象，先把下一个节点拿到手
                head->next = nullptr;
                
                int index = (head->val % N + N) % N;    //计算在新的hash中的位置
                if (result[index] == nullptr) {     // 特别注意：插入新的hash前，新的位置无元素直接插入
                    result[index] = head;
                } else {                            // 特别注意：新的位置有元素，插入到对应位置的"链表结尾"！
                    ListNode * cur = result[index];
                    while (cur->next != nullptr) { // 找到最后一个节点，然后挂上去
                        cur = cur->next;
                    }
                    cur->next = head;
                }
                
                head = nextNode;            //指向原始hash中该位置对应链表的下一个元素
            }
        }

        return result;
    }
};

代码

本文采用双向链表（list）和 hash表（unordered_map）来实现。

根据题目要求，当容量到达最大时，长时间不用的就要删除，而且最近访问的要优先保留，所以考虑使用双向链表来管理各个key值，即 list<int> mKeys;（通过将新元素插入到链表结尾，将最新访问的移动到链表的结尾，这样就可以在超过容量时，删除链表头，即删除长时间不用的元素）。对于重复插入相同的key，自然是先移动到链表尾部，再更新其值即可。这时，我们还需要一个容量来保存value值。考虑到要在该容器中以O(1)时间复杂度找到重复的key值，所以考虑使用 hash表，在C++中对应的数据结构是unordered_map，为了方便查找到hash中key在list中对应的位置，我们在 该哈希表中存入三个元素：key， value，以及key在list中对应的位置即list<int>::iterator，所以 定义 unordered_map<int, pair<int, list<int>::iterator> mData;

相关接口：list::push_back(x) / pop_front() / front() / erase(iter)

unordered_map::find(key) / erase(key)

class LRUCache {
private:
    list<int> mKeys; //使用双向链表存储所有的key值， // 以管理key的新旧
    unordered_map<int, pair<int,list<int>::iterator>> mData; // 使用hash表存储key值,value值,以及当前key在list中的位置
    int mCapacity;
private:
    void insert(int key, int value) {
        mKeys.push_back(key); //注意：list是双向链表，list::insert方法需要指定插入的位置。
        mData[key] = make_pair(value, --mKeys.end()); //注意pair是  value + key在list中的位置
    }

public:
    LRUCache(int capacity) {
        mCapacity = capacity;
    }
    
    int get(int key) {
        auto it = mData.find(key);
        if (it == mData.end()) {// 不存在，返回-1
            return -1;
        } else {                // 存在，该key移动到list的尾部，并更新hash中的key在list中的位置，并返回value值
            mKeys.erase(it->second.second);    // 根据迭代器，更新list中的key的位置
            mKeys.push_back(key);              // 放到list尾部 《======
            mData[key].second = --mKeys.end(); //更新hash中对应的list中的位置 //或 it->second.second = --mKeys.end();
            return mData[key].first;
        }
    }
    
    void put(int key, int value) {
        if (get(key) != -1) {   //若存在，则移动到list结尾，并更新它的值 《======
            mData[key].first = value;
        } else {                //若不存在，则插入新的值
            insert(key, value);
            if (mKeys.size() > mCapacity) { //若元素数量超过了容量，则删除最老的(队列头)key
                int oldKey = mKeys.front();  //注意：是 front() ！
                mKeys.pop_front();
                mData.erase(oldKey);
            }
        }
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

例9. 乱序字符串分组（anagrams）

描述：给出一个字符串数组S，找到其中所有的乱序字符串(Anagram)。如果一个字符串是乱序字符串，那么他存在一个字母集合相同，但顺序不同的字符串也在S中。所有的字符串都只包含小写字母。（来源：lintcode 171 · 乱序字符串 ≈ leetcode 49. 字母异位词分组 = leetcode 面试题 10.02. 变位词组）

样例1:
输入:["lint", "intl", "inlt", "code"]   输出:["lint", "inlt", "intl"]
样例 2:
输入:["ab", "ba", "cd", "dc", "e"]   输出: ["ab", "ba", "cd", "dc"]

代码

从题中可以看出：目的是找到含有相同字母的字符串，若含有相同字母的字符串个数大于1，就输出。看到“相同”两个字，首先就应该想到使用hash表（因为hash表在查找一个元素的时间复杂度最低位O(1)），又因为是anagram（变位词、相同字母异序词），所以要先将字符串中的字母进行排序，然后就可以比较是否相等，进而知道是否是同一个anagram。

注意string的排序，可以使用数组索引的方式（参考  string getSortedString(string &str) 采用一个 array[26] 数组的形式进行统计计数 array[char - 'a']++ ），也可以直接使用 std::sort(str.begin(), str.end()) 直接对字符串中的字母进行排序。

采用hash表时，以排好序的字符串作为key，以排序前的字符串组成的vector作为value,这样就可以很方便的找到anagrams, 然后，当 某个key对应的anagrams的个数大于1，就输出即可。

class Solution {
public:
    vector<string> anagrams(vector<string> &strs) {

        unordered_map<string,vector<string>> hash; //注意: 这里的定义很巧妙
        for(auto& str : strs){
            string key = str;
            sort(key.begin(), key.end());        //注意：对字符串中的字母进行排序
            hash[key].push_back(str);
        }

        vector<string> results;
        for(auto& result : hash){     // result 是 std::pair<const tring,vector<string>>
            if (result.second.size() <= 1) {
                continue;
            }
            for (int i = 0; i < result.second.size(); i++) {
                results.push_back(result.second[i]);
            }
        }

        return results;
    }
};

例10. 无序整数数组中 最长连续子序列

描述：给定一个未排序的整数数组num，找出最长连续序列的长度。要求你的算法复杂度为O(n)；len(num) <= 10000len(num)<=10000 （来源：lintcode 124 · 最长连续序列 = leetcode 128. 最长连续序列）
样例：
输入：num = [100, 4, 200, 1, 3, 2]   输出：4
解释：这个最长的连续序列是 [1, 2, 3, 4]. 返回所求长度 4

代码

本身是无序数组，要求算法复杂度是O(n)， 所以不能通过排序的方式解决。所以首先应该想到使用hash表。本题的特殊之处在于连续序列，意味着 每个答案中的元素相差1，所以可以考虑通过当前值num[i] 减1（pre），加1（next）的方式，看当前值的前后元素存不存在，若存在就删除对应的元素，然后继续分别加1，减1； 最终对于当前值num[i]来说，连续子序列的长度即为 next - pre - 1. 最后在所有长度中取最大即可。

class Solution {
public:
    int longestConsecutive(vector<int> &num) {
        int n = num.size();
        if (n == 0) { //该判断可以省略
            return 0;
        }

        int res = 0;
        unordered_set<int> hash(num.begin(), num.end()); //注意：这里的初始化很简洁！

        for (int i = 0; i < n; i++){
            if (hash.find(num[i]) != hash.end()) {
                hash.erase(num[i]);
                int pre  = num[i] - 1;
                int next = num[i] + 1;
                
                while (hash.find(pre) != hash.end()) {
                    hash.erase(pre);        // 注意：勿少
                    pre--;
                }
                while (hash.find(next) != hash.end()) {
                    hash.erase(next);       // 注意：勿少
                    next++;
                }

                res = max(res, next - pre - 1);
            }
        }

        return res;
    }
};

4. 堆 （heap）

例11. 寻找数据流的中位数

描述：中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。（来源：leetcode 295. 数据流的中位数 = leetcode  剑指 Offer 41. 数据流中的中位数 困难≈ lintcode 81 · 寻找数据流的中位数 困难）
例如，[2,3,4] 的中位数是 3；[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构：void addNum(int num) - 从数据流中添加一个整数到数据结构中。 double findMedian() - 返回目前所有元素的中位数。
示例：addNum(1)  addNum(2)  findMedian() -> 1.5  addNum(3)   findMedian() -> 2

代码

数据流中的中位数，意味着只有插入操作，每次插入中位数都有可能更新，即数据的存储结构应该是有序的。本文采用两个堆（对应的数据结构是 priority_queue, 当然也可以使用vector + std::push_heap/std::pop_heap模拟，参考 剑指offer面试题41）来实现，一个大顶堆（形象地认为在左侧），一个小顶堆（形象地认为在右侧），那么，[ mMax逐一pop的元素的集合(每次弹出都是最大的，从往左延伸着写)， mMin逐一pop的集合(每次弹出都是最小的，往右延伸着写)] 可以组成一个从左到右的递增序列。（当然堆内是一颗完全二叉树，依次pop可以pop出有序序列，参考 C++_数据结构_堆用法详解）

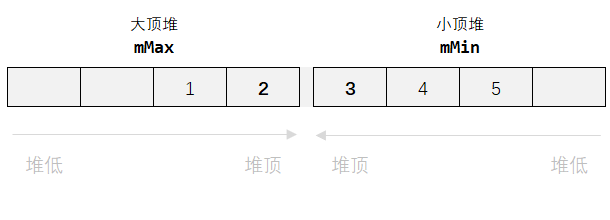
有了上述直观的理解后，则中位数就只跟 mMax.top() 和 mMin.top() 有关了。

为了找到中位数，我们需要将数据均匀分布在这两个堆中，本文采用先插入小顶堆的方式（即，目前元素总个数是偶数是插入小顶堆mMin, 奇数时插入大顶堆mMax）同时，考虑在插入小顶堆时，若当前元素 比 小顶堆的最小元素（mMin.top()）还小，就应该插入到大顶堆，并且把大顶堆的最大元素（mMax.top()）拿出来作为补偿给小顶堆。在插入大顶堆时，若当前元素比mMax.top() 还大，就插入小顶堆，并把小顶堆的最小值给到大顶堆。这样一来，中值在总元素是奇数个时，就是 mMin.top(), 在总元素是偶数个数，就是 (mMax.top() + mMin.top()) / 2.0; 注意这里是 除以 2.0，因为按要求结果可能是浮点数。 题目 lintcode 81 · 寻找数据流的中位数 中的要求的中位数与该题大同小异，求的是总共n个元素中的 索引为 (n-1)/2 的元素（对应的中位数：共奇数个还是mMin.top()， 偶数个则是 mMax.top()）。

class MedianFinder {
private:
    priority_queue<int> mMax;       //默认是大顶堆，仿函数是less<int> top是最大的
    priority_queue<int, vector<int>, greater<int>> mMin;  //小顶堆  注意greater<int>后面没有()  // top是最小的

public:
    MedianFinder() {     //初始化先清空下
        while(mMax.size() > 0) {
            mMax.pop();
        }
        while(mMin.size() > 0) {
            mMin.pop();
        }
    }
    
    void addNum(int num) {
        int n = mMax.size() + mMin.size();
        if ( n % 2 == 0) { //原来总共偶数个元素，插入mMin堆
            if ( mMax.size() > 0 && num < mMax.top()) {//若当前元素比小顶堆的最小元素还小，
                mMax.push(num);     // 就应该插入到大顶堆，
                num = mMax.top();   // 并且把大顶堆的最大元素（mMax.top()）拿出来作为补偿给小顶堆。
                mMax.pop();
            }
            mMin.push(num);
        } else {            //原来总共奇数个元素，插入mMax堆
            if (mMin.size() > 0 && num > mMin.top()) {
                mMin.push(num);
                num = mMin.top();
                mMin.pop();
            }
            mMax.push(num);
        }
    }
    
    double findMedian() {
        int n = mMax.size() + mMin.size();
        if (n % 2 == 1) {
            return mMin.top();
        } else {
            return (mMax.top() + mMin.top()) / 2.0; // 有的地方中值定义成索引为(n-1)/2的元素，则return mMax.top();
        }
    }
};

相关题目：未排序数组中的中位数 ，两个排序数组的中位数

例12. 堆化操作 siftdown

描述：给出一个整数数组，把它变成一个最小堆数组（小顶堆），这称为堆化操作。对于堆数组A，A[0]是堆的根，并对于每个A[i]，A [i * 2 + 1]是A[i]的左儿子并且A[i * 2 + 2]是A[i]的右儿子。

什么是堆？ 什么是堆化？ 如果有很多种堆化的结果？
堆是一种数据结构，它通常有三种方法：push， pop 和 top。其中，“push”添加新的元素进入堆，“pop”删除堆中最小/最大元素，“top”返回堆中最小/最大元素。把一个无序整数数组变成一个堆数组。如果是最小堆，每个元素A[i]，我们将得到 A[i * 2 + 1] >= A[i] 和 A[i * 2 + 2] >= A[i] 返回其中任何一个。

样例：输入 : [3,2,1,4,5]   输出 : [1,2,3,4,5]    解释 : 返回任何一个合法的堆数组
挑战 ：O(n)的时间复杂度完成堆化

代码

该题考察的是模拟  std::make_heap() 操作。本文使用 siftdown  的方法：从索引为 N/2 的元素 向 索引为 0 的元素 依次遍历； 在一个while循环中（相当于树结构上从叶节点到根节点向上递归），对于每个元素（索引为i ）找它的 左子节点（2i +1） 和 右子节点 （2i + 2），在这三者中找到最小的（索引为 smallest ），然后交换当前元素 i 和 smallest 对应的元素， 然后把当前元素（在新的位置 i = smallest） 作为新的根节点，执行上述同样的操作，直到没有叶节点。特别注意，代码中找根/左子节点/右子节点时，比较的对象是 A[smallest]。

class Solution {
public:
    void heapify(vector<int> &A) { //一句话的话就是：std::make_heap(A.begin(), A.end(), greater<int>());
        int n = A.size();
        if (n <= 1) {
            return;
        }

        for (int i = n / 2; i >= 0; i--) { //从最低层最右侧的根节点开始向上遍历 siftdown 操作
            siftdown(A, i);
        }
    }

    void siftdown(vector<int> &A, int i) {
        while (i < A.size()) {
            int smallest = i;       //特别注意：下面比较的是 A[smallest] 而不是 A[i], 因为一次if后， smallest 可能发生变化
            if (2 * i + 1 < A.size() && A[2 * i + 1] < A[smallest]) { //若当前节点的左子节点存在且更小，就将该索引当成最小
                smallest = 2 * i + 1;
            }
            if (2 * i + 2 < A.size() && A[2 * i + 2] < A[smallest]) { //若当前节点的右子节点存在且更小，就将该索引当成最小
                smallest = 2 * i + 2;
            }
            if (smallest == i) { //比较后，发现当前节点作为根节点仍是最小，就不必操作，直接返回
                break;
            }

            std::swap(A[i], A[smallest]);
            
            i = smallest;   //精华代码：将最小的位置现在的值（还是交换前的A[i]）当做根，循环的看左右子节点是否有更小需要交换。
        }
    }
};

例13. 找从小到大的第n个丑数

描述：给你一个整数 n ，请你找出并返回第 n 个 丑数 。丑数 就是只包含质因数 2、3 和/或 5 的正整数。（来源：leetcode 264. 丑数 II = leetcode 剑指 Offer 49. 丑数）
示例 1：
输入：n = 10  输出：12
解释：[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。

示例 2：
输入：n = 1  输出：1
解释：1 通常被视为丑数。

代码

本题有多种方法（比如动态规划），本文采用小顶堆的方式。初始时堆为空。首先将最小的丑数 1加入堆。每次取出堆顶元素 x，则 x 是堆中最小的丑数，由于 2x, 3x, 5x 也是丑数，因此将 2x, 3x, 5x 加入堆。上述做法会导致堆中出现重复元素的情况。为了避免重复元素，可以使用哈希集合去重，避免相同元素多次加入堆。在排除重复元素的情况下，第 n 次从最小堆中取出的元素即为第 n 个丑数。

利用的性质：优先队列（此处用 最小堆）的排序性质（每次弹出的都是最小的值），循环pop n次即得到第n个丑数； hash的无重复性质  和  find一个元素O(1)时间复杂度的性质。

class Solution {
public:
    int nthUglyNumber(int n) {
        if (n <= 0) {
            return -1;
        }

        priority_queue<long, vector<long>, greater<long>> que; //定义最小堆，存储丑数
        unordered_set<long> hash;    //使用 hash来保证 堆中元素不重复，这样，在每次循环中，一次从优先队列中取出一个元素，取的第n次就是第n个丑数
        vector<int> factor = {2, 3, 5};
        
        int res;
        que.push(1L);
        hash.insert(1L);
        
        for (int i = 0; i < n; i++) {
            long cur = que.top();
            que.pop();
            res = (int)cur;
            for (int j = 0; j < factor.size(); j++) {
                long tmp = cur * factor[j]; // 注意：这里是 索引j 别写错了
                if (hash.find(tmp) == hash.end()) { // hash中未曾出现过，就插入hash，同时插入小顶堆
                    hash.insert(tmp);
                    que.push(tmp);
                }
            }
        }

        return res;
    }
};

时间复杂度分析：O(nlogn) 因为找第n个丑数，所以for循环n次，每次循环中，要进行一次堆（priority_queue）的插入操作（O(logn)）(当然hash的find和insert操作时间复杂度是O(1)), 所以综合起来是 O(nlogn)；空间复杂度是O(n)。

堆的操作 时间复杂度：插入 O(logn), 比如采用siftup的方法； 删除 O(logn) , 比如采用siftdown的方法；取最大最小 O(1) 时间复杂度。

最后

以上就是成就缘分为你收集整理的算法笔记_面试题_21.数据结构相关_模板及示例十几道1. 栈相关（stack）2. 单调栈3. 哈希表(or 散列表) （hash table）4. 堆 （heap）的全部内容，希望文章能够帮你解决算法笔记_面试题_21.数据结构相关_模板及示例十几道1. 栈相关（stack）2. 单调栈3. 哈希表(or 散列表) （hash table）4. 堆 （heap）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。