【笔记】概述胶囊网络

• 1. CNN现存问题
  • 池化操作提供了局部不变性，错误解决了需要解决的等变性问题，从而丢失了位置等信息。
  • 平移等变性：对于一个函数，如果对其输入施加的变换也会同样反映在输出上，那么这个函数就对该变换具有等变性。
  • 平移不变性：对一个函数，若对其输入施加的某种操作丝毫不会影响到输出，那么这个函数就对该变换具有不变性。
• 2. 胶囊网络的改进
  • 使用胶囊作为网络的基本单元
  • 特征向量表示可视实体，对方位等信息进行编码
  • 动态路由算法代替池化操作
    
• 3. 特征向量表示可视实体
  • 特征向量长度表示实体存在概率；各维特征表示实体姿态
  • 实体的存在概率具有局部不变性。当胶囊覆盖的有限视域内的实体变换姿态时，它是不变的。
  • 实体的实例化参数（尺度、方向等）具有等变性。由于实例化参数表示实体的姿态坐标，因此随着实体的姿态变化，实例化参数会相应改变。
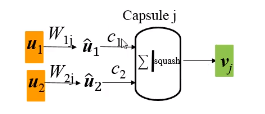
• 4. 胶囊
  • 胶囊输出的实例化参数提供了一种由部分到整体的简单识别方法，由单个有限视觉域逐层向上预测，最终形成对目标图像的解析树，达到识别目的。
  • 在连接到下一层时，可以做一个简单选择——实体是否能够由多个激活的具有正确的空间关系的胶囊表示，并且激活更高级别的胶囊。

• 设胶囊的输入为$u_i$，使用预测矩阵$W_{ij}$与$u_i$,对高层特征向量进行预测，得到预测的特征向量$u_{j|i}$，$u_{j|i}=W_{ij}{u}_i$
• 当前层胶囊对所有预测向量求加权平均，便得到向量$s_j$，$s_j={\sum }_i{c}_{ij}{u}_{j|i}$。其中，$c_{ij}$称作耦合系数。
• 为了使特征向量的长度能够表示实体存在的概率，需要使用非线性压缩函数将向量长度限制在0-1之间。$v_j=\frac{{\Vert s_j\Vert }^2}{1+{\Vert s_j\Vert }^2}\frac{s_j}{\Vert s_j\Vert }$

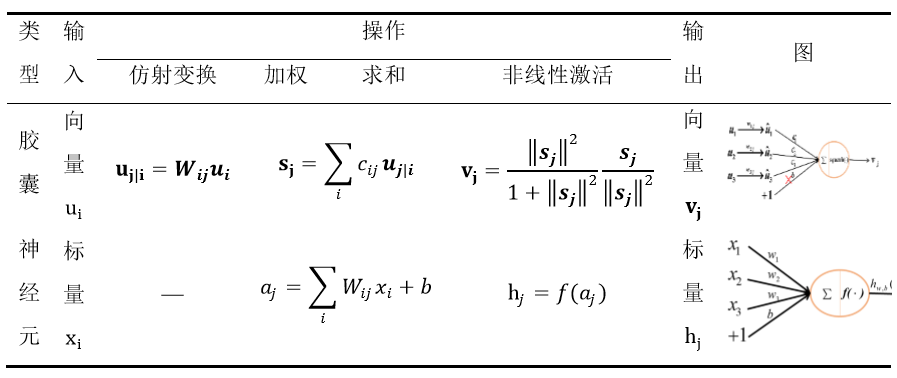
• 5. 胶囊与神经元对比
  
• 6. 胶囊间的动态路由
  • 胶囊间的动态路由机制可以确保每一层胶囊输出的特征向量被正确地发送到下一层中对应的胶囊。
  • 耦合系数$c_{ij}$是使用Softmax函数来计算的，并且前一层的胶囊i与下一层中的所有胶囊之间的耦合系数总和为1。$c_{ij}=\frac{exp(b_{ij})}{{\sum }_{k}exp(b_{ik})}$
    • 其中，$b_{ij}$为胶囊i应该耦合到胶囊j的对数先验概率，它取决于两个胶囊的类型和位置，与当前的输入图像无关，其初始值为0，然后通过预测向量$u_{j|i}$和实际输出向量$v_j$的一致性来修正。
    • 一个简单的表明一致性关系的函数就是标量积，在计算新的耦合系数之前，要把$a_{ij}=v_j{u}_{j|i}$加到初始的$b_{ij}$上。
  • 特别注意的是其整个路由过程不仅仅是存在于胶囊网络的训练过程中，也存在于验证和测试过程中，而且需要迭代多次。
    
• 7. CapsNet
  • 7.1 网络基本结构
    • 实现从主胶囊（8D）到数字胶囊（16D）的转换，即低级特征向量向高级特征向量的转换
    • 由于使用特征向量长度来表示对应类别存在概率，所以在最后一层进行分类时需要将输出的特征向量取L2范数
  • 7.2 边际损失函数
    • 为实现同时对多个对象的识别，每类目标对象对应的胶囊应分别使用边际损失函数得到类损失函数$L_k$，则总边际损失是所有类损失之和。
      $L_k=T_{k}max(0,m^{+}-\Vert v_k\Vert {)}^2+\lambda (1-T_k)max(0,\Vert v_k\Vert -m^{-}{)}^2$
      • $T_k$表示k类目标是否存在。当k类目标对象存在时为1，不存在时为0。
      • $m^{+}$是上界，一般取0.9。
      • $m^{-}$是下界，一般取0.1。
      • $\lambda$为不存在的对象类别的损失的下调权重，避免最开始从不存在分类对应的胶囊输出的特征向量中学习，一般取0.5.
  • 7.3 重构正则化
    • 鲁棒性强的模型一定具有很强的重构能力。为了使胶囊对输入图像进行编码并输出对应实例化参数，该网络引入了一个重构损失作为正则项。重构损失是逻辑单元的输出和像素强度之间的差的平方和。

最后

以上就是慈祥画板为你收集整理的【笔记】概述胶囊网络的全部内容，希望文章能够帮你解决【笔记】概述胶囊网络所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。