【机器视觉】(北邮版）卷积，图像降噪，边缘提取，纹理表示

梯度是链式法则，连乘–》容易造成梯度消失
Dropout:随机失活~

卷积与图像去噪

对一个像素点做卷积–》推广到所有像素点
卷积核：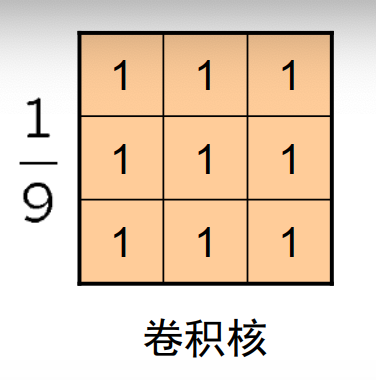
注意：卷积核需要先翻转才能做滤波，不然不叫做卷积，叫滤波

卷积性质：
1、叠加性
2、平移不变性

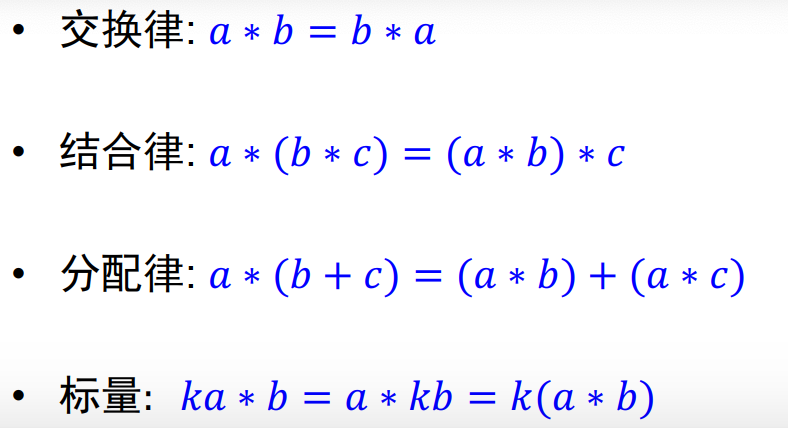
边界填充：
不填充会导致图像边界小一圈
0填充：Zero-padding
其他填充方法：拉伸，镜像
卷积操作后的图像要小于输入时图像，通过边界填充，我们可以实现卷积前后图像的尺寸不变；

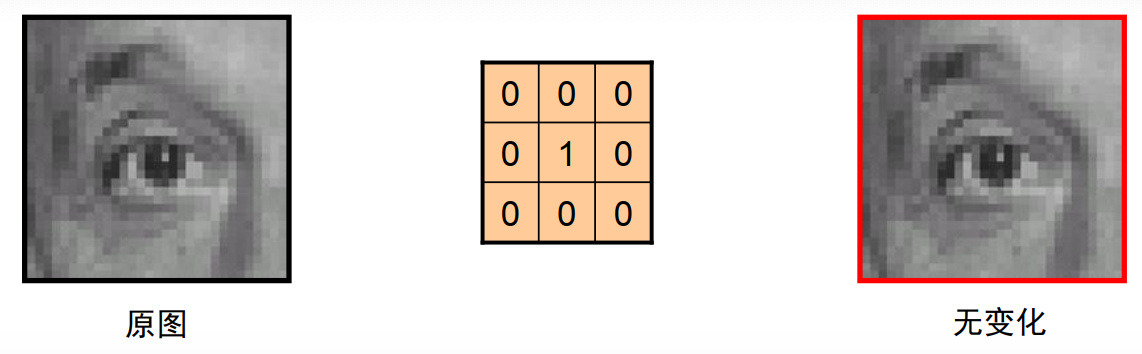
卷积示例：
单位脉冲：无变化


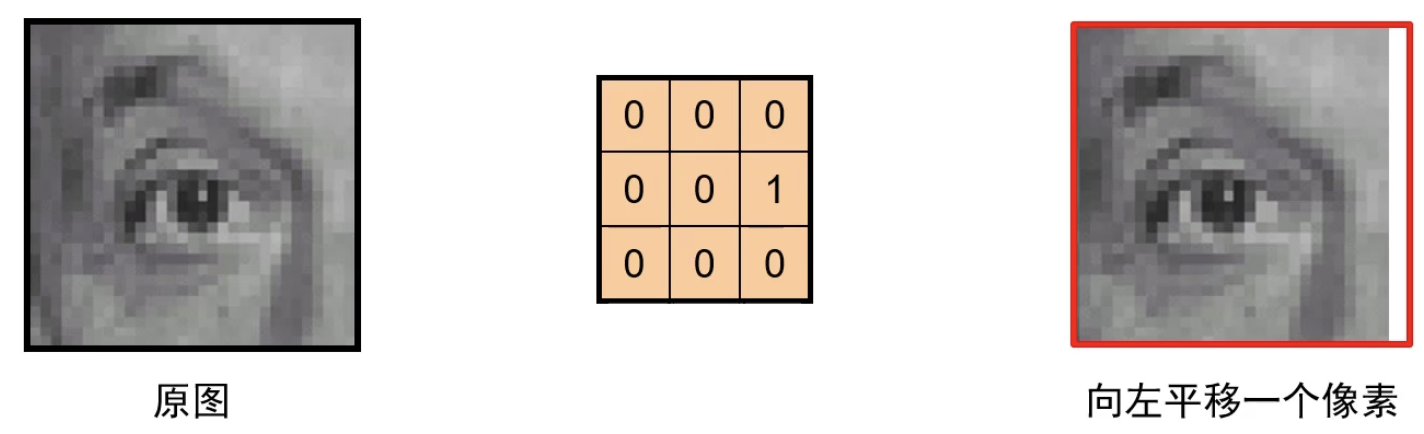
平滑：

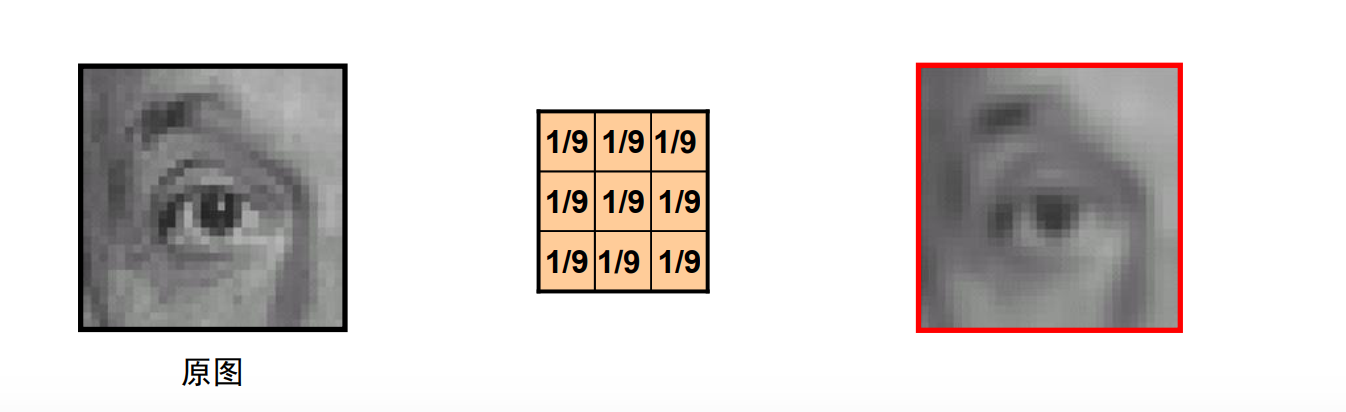
锐化：

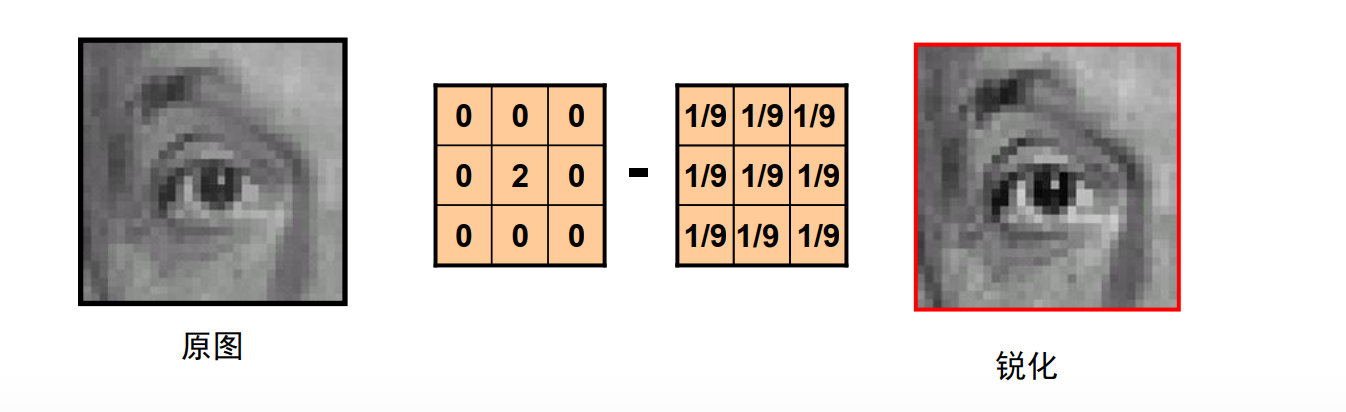
原图-平滑=细节
原图+细节=锐化

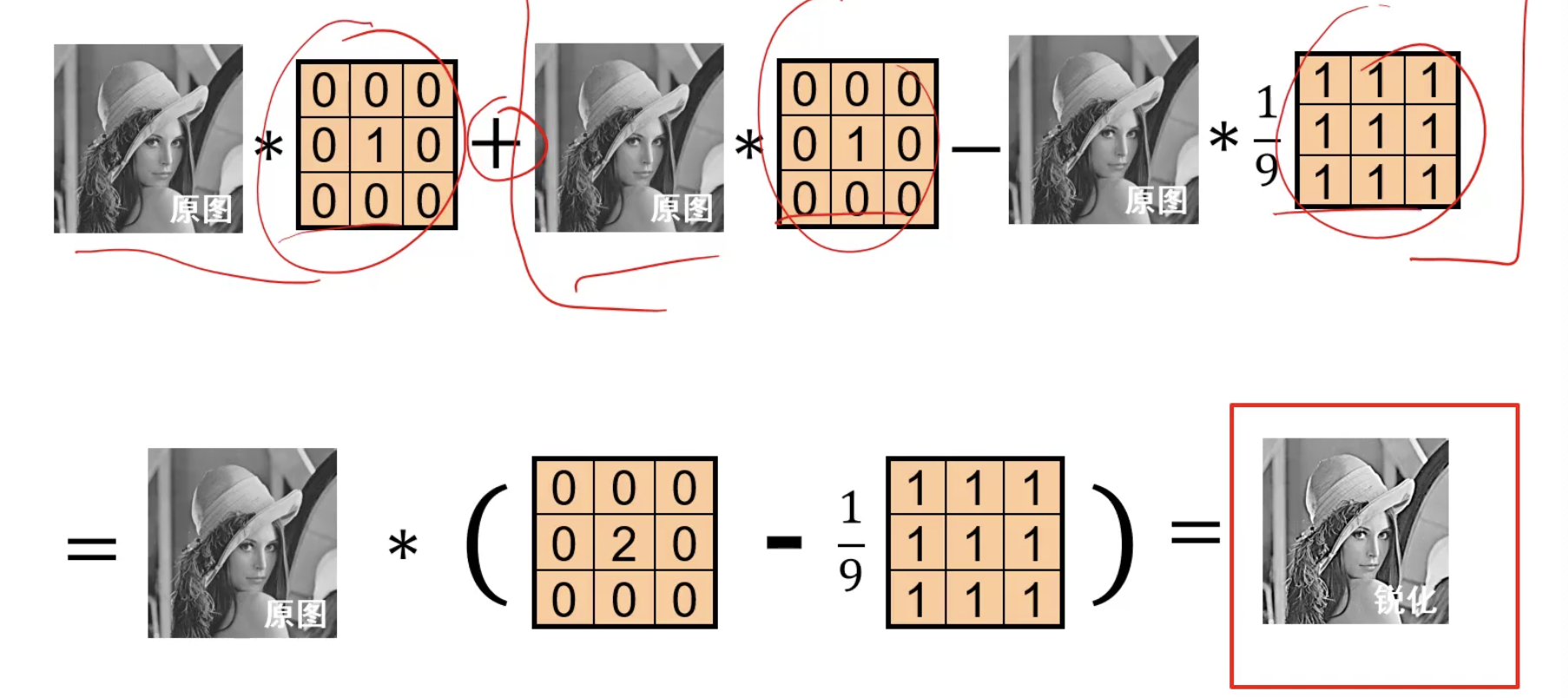
高斯卷积核：

振铃：卷积后的图像产生了一些水平和竖直的条状！！！
解决办法：


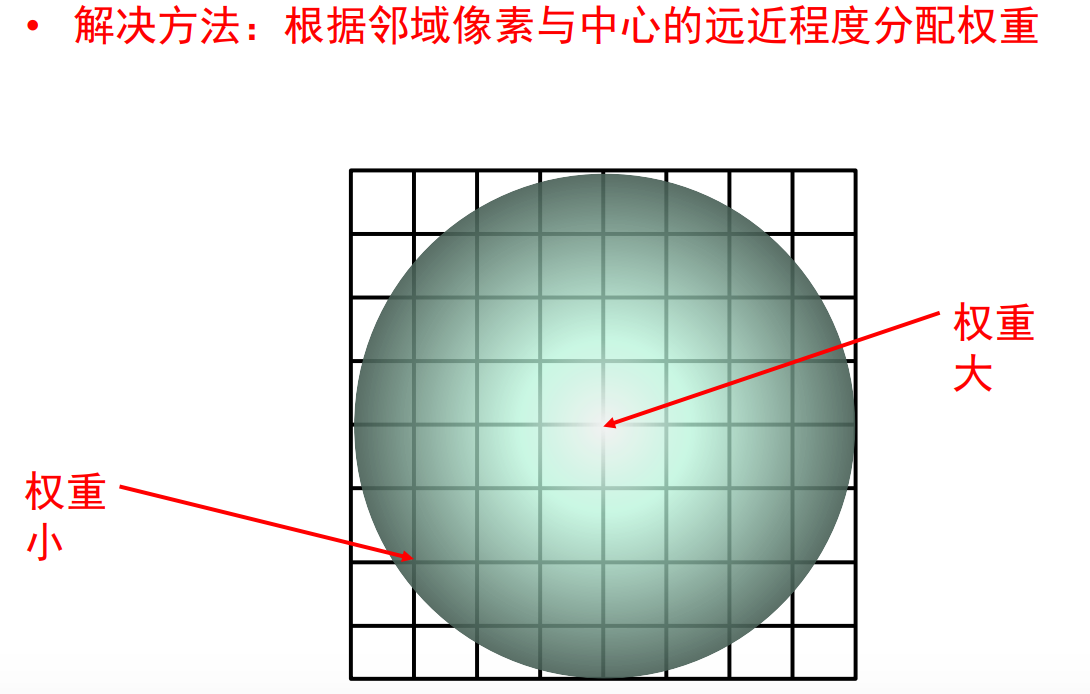
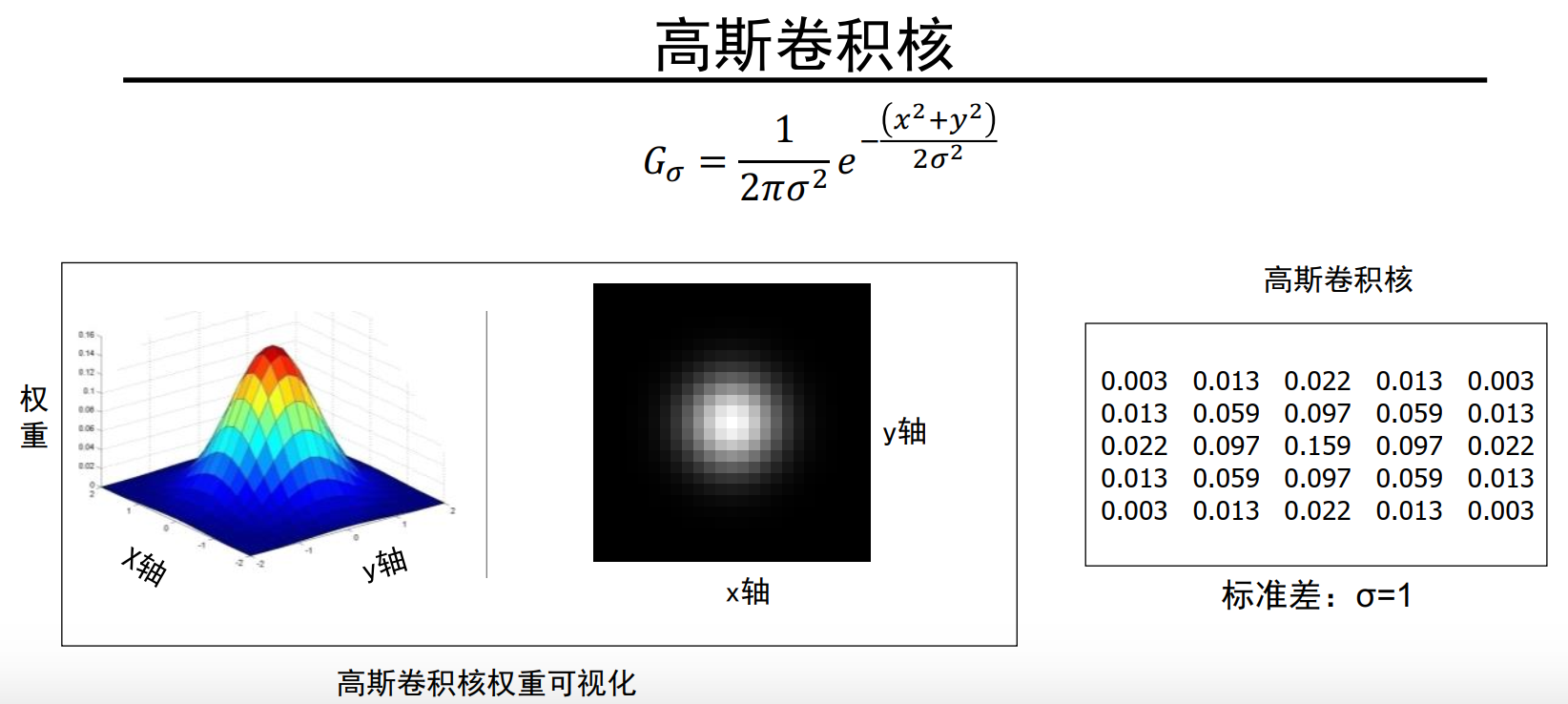
生成步骤：

1. 确定卷积核的尺寸,比如 5 × 5
2. 设置高斯函数的标准差，比如σ=1
   
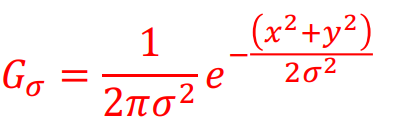
3. 计算卷积核各个位置权重值
4. 对权重值进行归一化（所有权值加和为1）

关键参数：
1、卷积核的尺寸
2、高斯函数的标准差

方差越大，平滑效果越明显~（方差越大中间那个点的权重越低！）
模板尺寸越大，平滑效果越强~

高斯卷积核：去除图像中的”高频“成分（可以看做是低通滤波器）

两个高斯卷积核卷积后得到的还是高斯卷积核：使用标准差为 σ 的高斯核进行两次卷积与使用标准差 σ 2 的高斯核进行一次卷积相同。

可分离：可以分解为两个一维高斯的乘积~

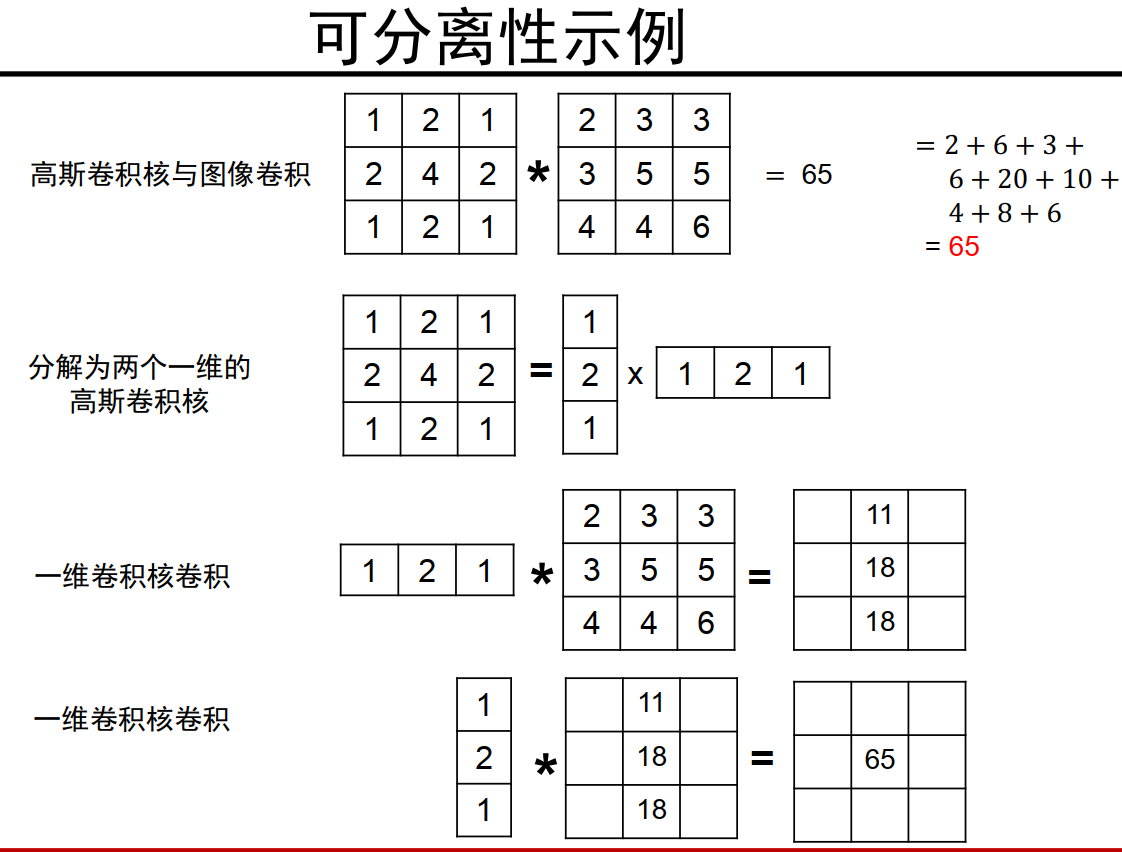
小模板多次卷积运算量要更低

新的卷积核，高斯卷积核，它能够有效地抑制噪声、实现图像平滑

图像噪声与中值滤波器

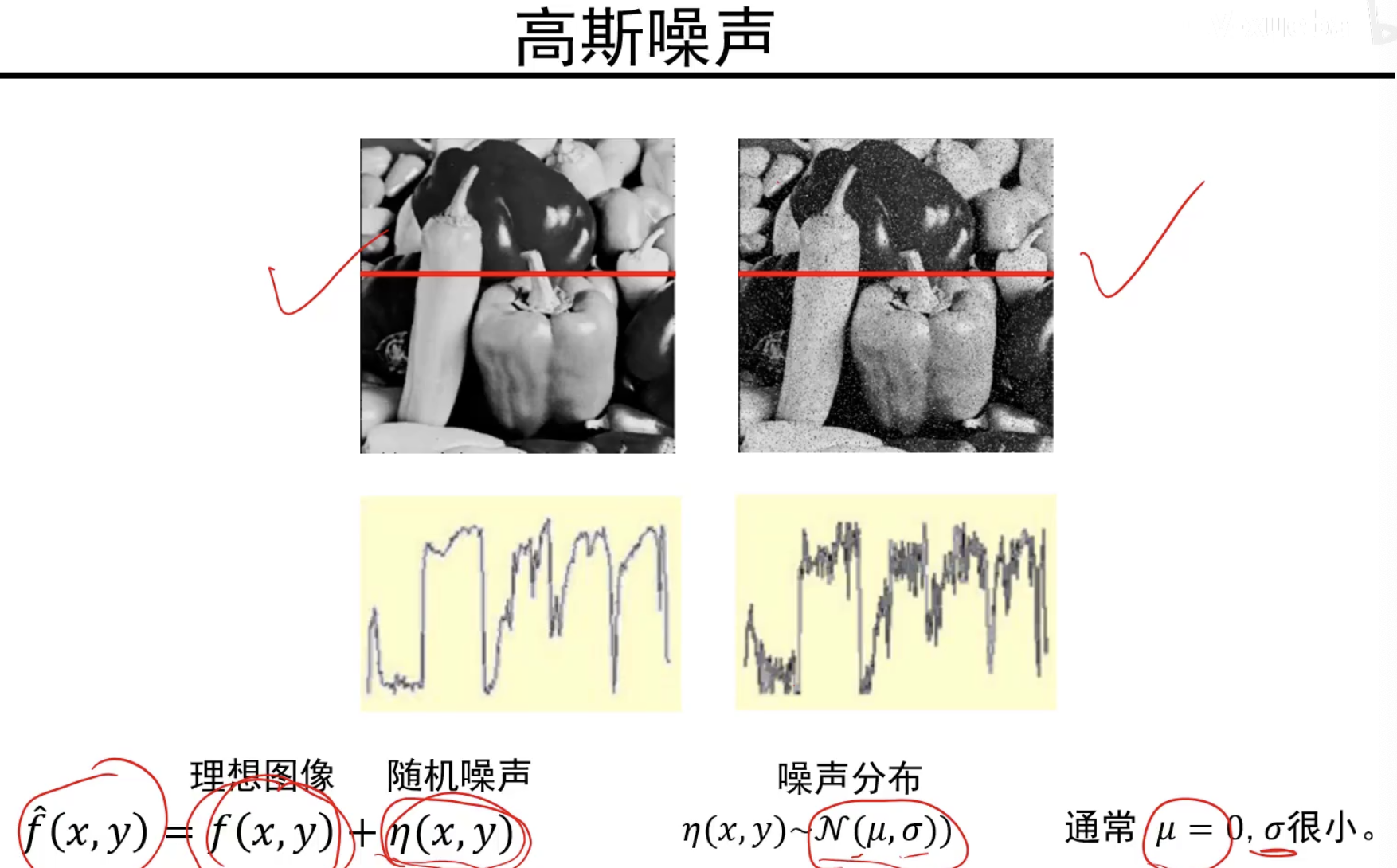
高斯去噪~

中值滤波：用中值去替换掉原来的值，这个值必定是原图上的某个像素，效果：

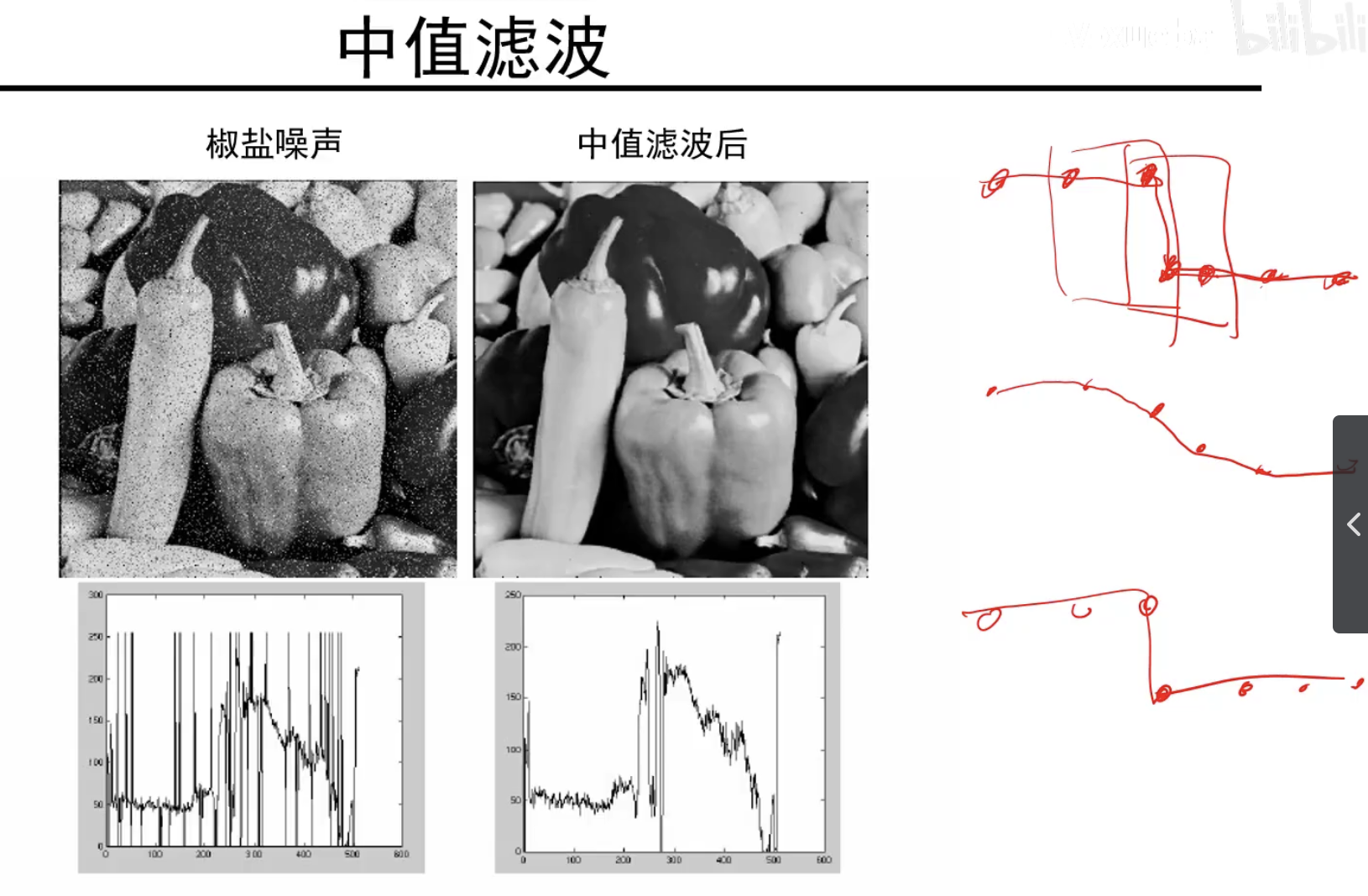
高斯卷积核是一个线性操作：

卷积与边缘提取：

边缘:图像中亮度明显而急剧变化的点

为什么要研究边缘？：
编码图像中的语义与形状信息
相对于像素表示，边缘表示显然更加紧凑

图像求导：
对X方向求导得到Y方向的边，反之亦然

梯度指向灰度变化最快的方向
梯度的模值越大，越可能是边界：

高斯一阶偏导卷积核：

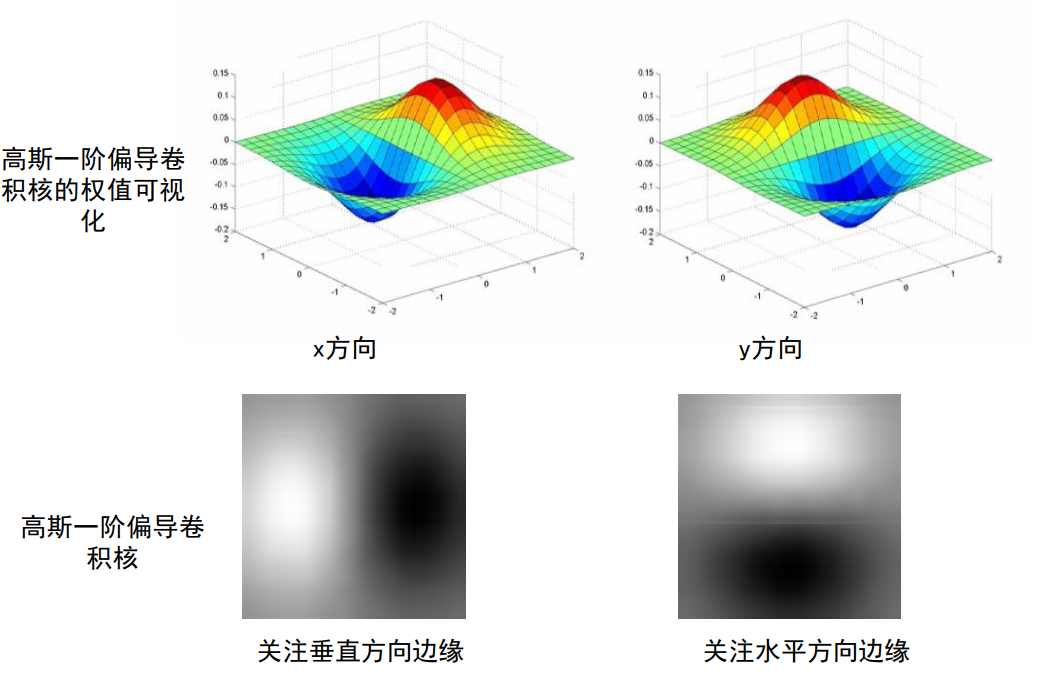
该模板只由方差决定：
方差越大，得到特征越粗犷，越小越精致

比较：

非最大化抑制：

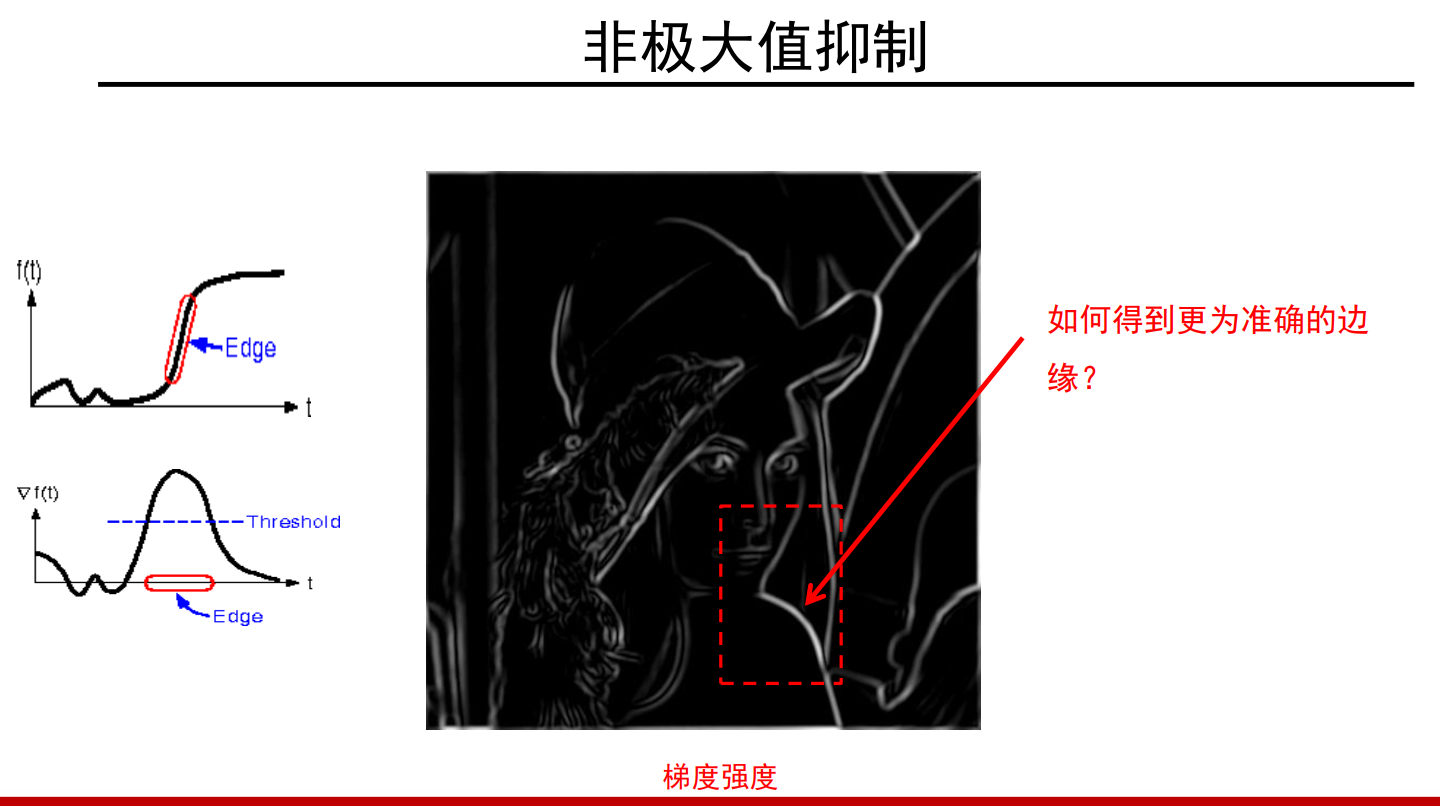
非极大值抑制：把厚边变薄

两个高斯核可以分离
两个高斯核卷积之后还是卷积核

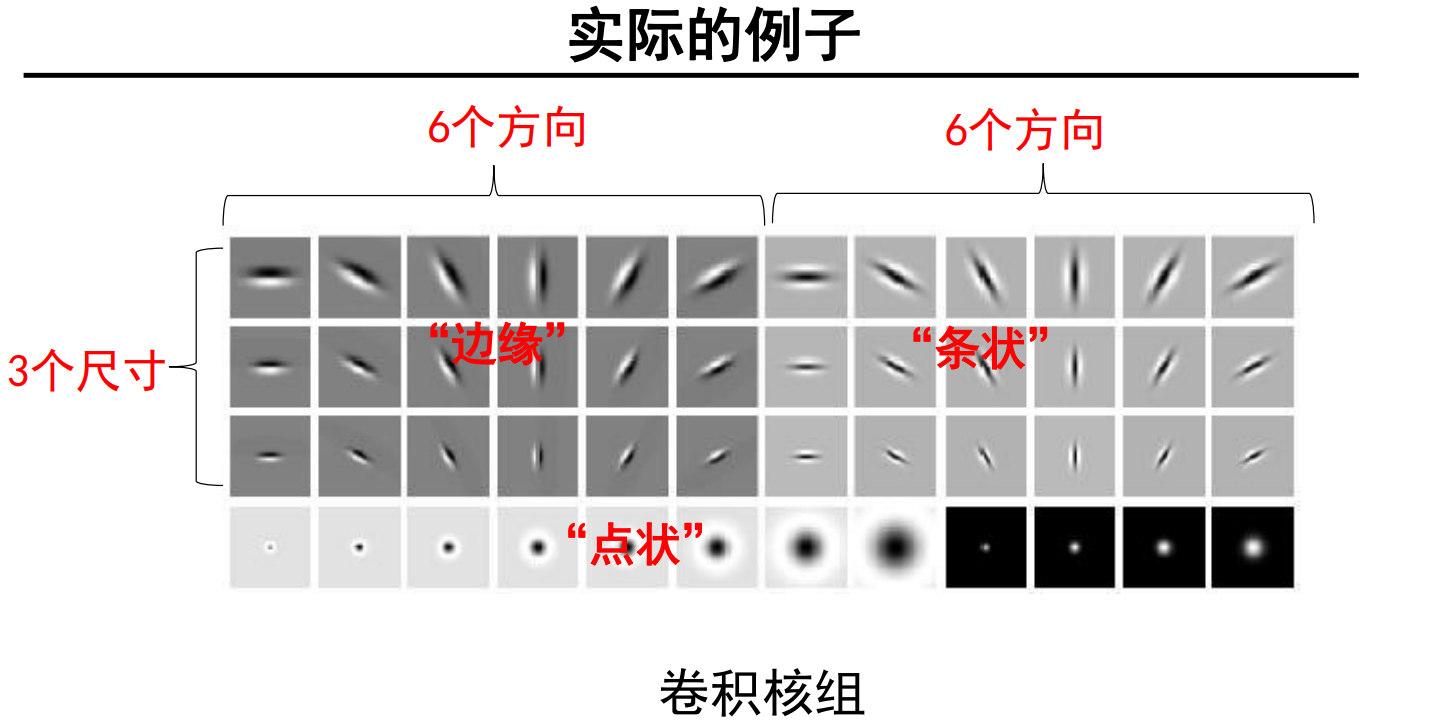
纹理表示：

思路：利用卷积核组提取图像中的纹理基； 利用基元的统计信息来表示图像中的纹理

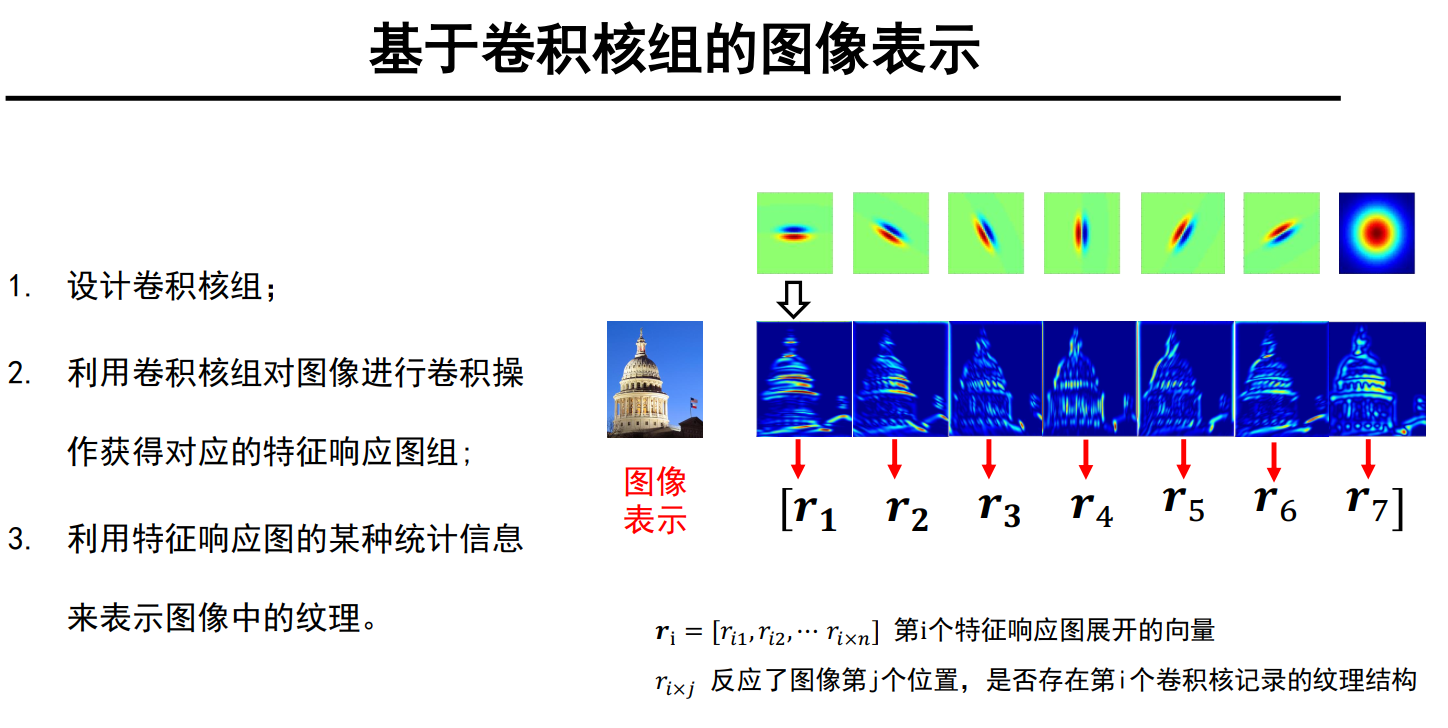
最后

以上就是痴情朋友最近收集整理的关于【机器视觉】(北邮版）卷积，图像降噪，边缘提取，纹理表示的全部内容，更多相关【机器视觉】(北邮版）卷积内容请搜索靠谱客的其他文章。