基础算法（冒泡、选择、插入、快速）

63 阅读 0 评论 42 点赞

我是靠谱客的博主自然方盒，最近开发中收集的这篇文章主要介绍基础算法（冒泡、选择、插入、快速），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1.冒泡排序

**
原理：1、从第一个数据开始，与第二个数据相比较，如果第二个数据小于第一个数据，则交换两个数据的位置。
　　2、指针由第一个数据移向第二个数据，第二个数据与第三个数据相比较，如果第三个数据小于第二个数据，则交换两个数据的位置。
　　3、依此类推，完成第一轮排序。第一轮排序结束后，最大的元素被移到了最右面。
　　4、依照上面的过程进行第二轮排序，将第二大的排在倒数第二的位置。
5、重复上述过程，没排完一轮，比较次数就减少一次。

图解:
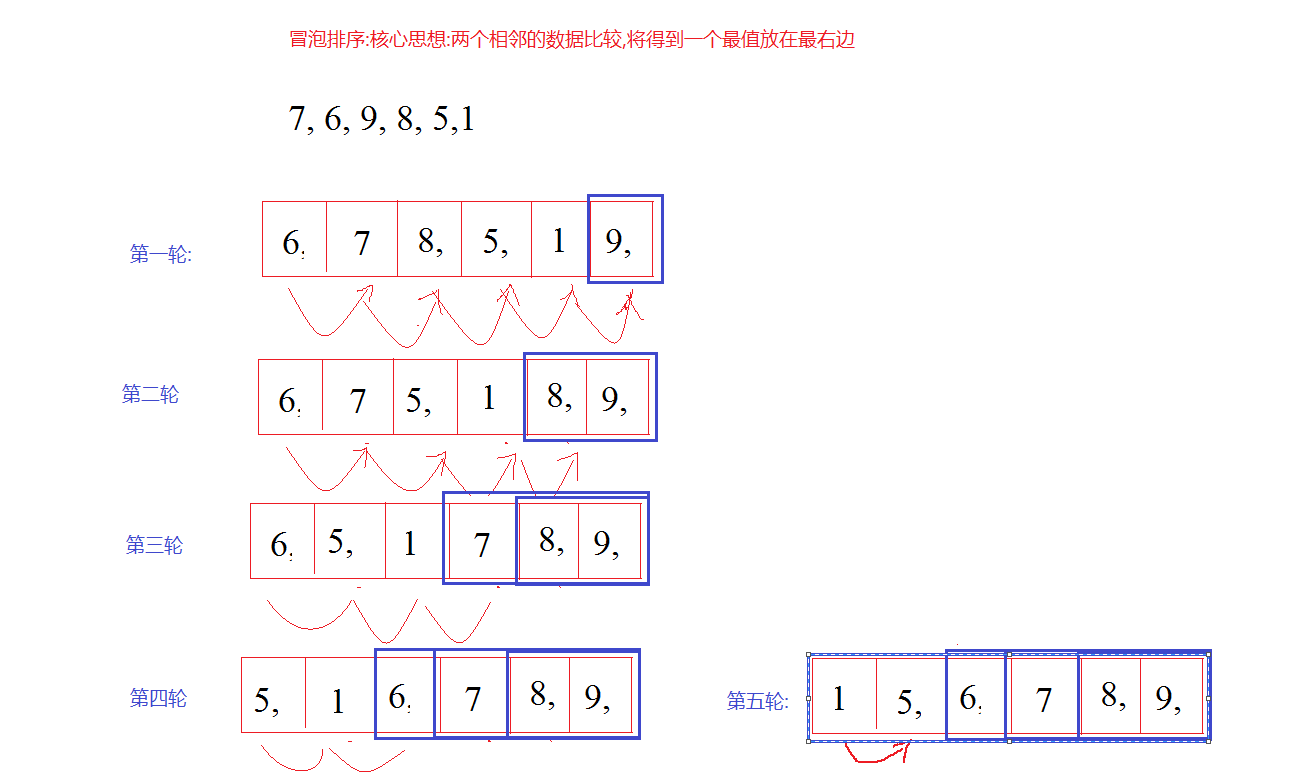
在这里插入图片描述
例子：待排序数据：7, 6, 9, 8, 5,1
第一轮排序过程：指针先指向7，7和6比较，6<7，交换6和7的位置，结果为：6,7,9,8,5,1
　　　　　　　　指针指向第二个元素7，7和9比较，9>7，不用交换位置，结果仍为：6,7,9,8,5,1
　　　　　　　　指针指向第三个元素9，比较9和8，8<9，交换8和9的位置，结果为：6,7,8,9,5,1
　　　　　　　　指针指向第四个元素9，比较9和5，5<9，交换5和9，结果为：6,7,8,5,9,1
　　　　　　　　指针指向第五个元素9，比较9和1，1<9，交换1和9的位置，结果为6,7,8,5,1,9
第一轮排序结束后，最大的数字9被移到了最右边。
进行第二轮排序，过程同上，只是由于最大的9已经放在最右边了，因此不用在比较9了，少了一次比较，第二轮结束的结果为：6,7,5,1,8,9
第三轮结果：6,5,1,7,8,9
第四轮比较结果：5,1,6,7,8,9
第五轮比较结果：1,5,6,7,8,9
最终排序结果为：1,5,6,7,8,9，由上可知N个数据排序，需要进行N-1轮排序；第i轮排序需要的比较次数为N-i次。

总结：N个元素需要排序N-1轮；第i轮需要比较N-i次；N个元素排序，需要比较n（n-1）/2次；冒泡排序的算法复杂度较高，为O（n*n）

package practice1;

import java.util.Arrays;

public class InsertSort {
	public static void main(String[] args) {
		int[] a = { 7, 6, 9, 8, 5,1 };
		insertSort(a);
		System.out.println(Arrays.toString(a));

	}

	public static void insertSort(int[] arr) {
		for (int i = 1; i < arr.length; i++) {
			int temp = arr[i];
			int leftIndex = i - 1;
			while (leftIndex >= 0 && arr[leftIndex] > temp) {
				arr[leftIndex + 1] = arr[leftIndex];
				leftIndex--;
			}
			arr[leftIndex + 1] = temp;
		}
	}
//	
}

2.选择排序

原理：
1、从第一个元素开始，分别与后面的元素向比较，找到最小的元素与第一个元素交换位置；
　　 2、从第二个元素开始，分别与后面的元素相比较，找到剩余元素中最小的元素，与第二个元素交换；
　　 3、重复上述步骤，直到所有的元素都排成由小到大为止。
　　
图解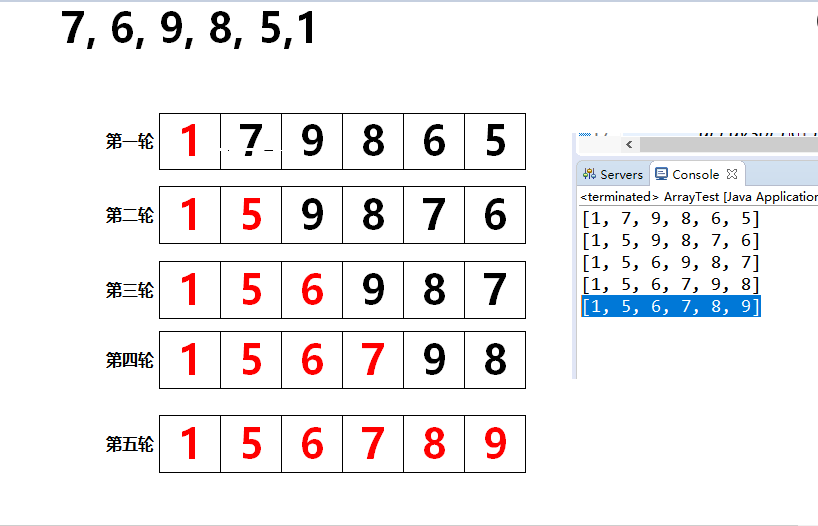：在这里插入图片描述
总结：N个元素需要排序N-1轮；第i轮需要比较N-i次；N个元素排序，需要比较n（n-1）/2次；选择排序的算法复杂度仍为O（n*n）；相比于冒泡排序，选择排序的交换次数大大减少，因此速度要快于冒泡排序

package practice1;

import java.util.Arrays;

public class SelectSort {
	public static void main(String[] args) {
		int[] a = { 7, 6, 9, 8, 5,1 };
		selectSort(a);
	}

	public static void selectSort(int[] arr) {
		int temp = 0;
		for (int i = 0; i < arr.length - 1; i++) {
			for (int j = i + 1; j < arr.length; j++) {
				if (arr[i] > arr[j]) {
					temp = arr[i];
					arr[i] = arr[j];
					arr[j] = temp;
				}
			}
		}
		System.out.println(Arrays.toString(arr));
	}
}

3.插入排序

原理：1、将指针指向某个元素，假设该元素左侧的元素全部有序，将该元素抽取出来，然后按照从右往左的顺序分别与其左边的元素比较，遇到比其大的元素便将元素右移，直到找到比该元素小的元素或者找到最左面发现其左侧的元素都比它大，停止；
2、此时会出现一个空位，将该元素放入到空位中，此时该元素左侧的元素都比它小，右侧的元素都比它大；
3、指针向后移动一位，重复上述过程。每操作一轮，左侧有序元素都增加一个，右侧无序元素都减少一个。

图解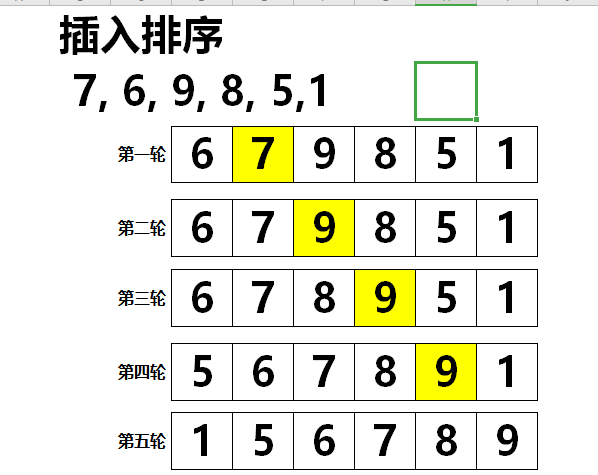：在这里插入图片描述
待比较数据：7, 6, 9, 8, 5,1
　　第一轮：指针指向第二个元素6，假设6左面的元素为有序的，将6抽离出来，形成7,,9,8,5,1，从7开始，6和7比较，发现7>6。将7右移，形成,7,9,8,5,1，6插入到7前面的空位，结果：6,7,9,8,5,1
　　第二轮：指针指向第三个元素9，此时其左面的元素6,7为有序的，将9抽离出来，形成6,7,,8,5,1，从7开始，依次与9比较，发现9左侧的元素都比9小，于是无需移动，把9放到空位中，结果仍为：6,7,9,8,5,1
　　第三轮：指针指向第四个元素8，此时其左面的元素6,7,9为有序的，将8抽离出来，形成6,7,9,,5,1，从9开始，依次与8比较，发现8<9，将9向后移，形成6,7,,9,5,1，8插入到空位中，结果为：6,7,8,9,5,1
　　第四轮：指针指向第五个元素5，此时其左面的元素6,7,8,9为有序的，将5抽离出来，形成6,7,8,9,,1，从9开始依次与5比较，发现5比其左侧所有元素都小，5左侧元素全部向右移动，形成_,6,7,8,9,1，将5放入空位，结果5,6,7,8,9,1。
　　第五轮：同上，1被移到最左面，最后结果：1,5,6,7,8,9。

总结：时间复杂度，由于仍然需要两层循环，插入排序的时间复杂度仍然为O(nn)。
　　比较次数：在第一轮排序中，插入排序最多比较一次；在第二轮排序中插入排序最多比较二次；以此类推，最后一轮排序时，最多比较N-1次，因此插入排序的最多比较次数为1+2+…+N-1=N(N-1)/2。尽管如此，实际上插入排序很少会真的比较这么多次，因为一旦发现左侧有比目标元素小的元素，比较就停止了，因此，插入排序平均比较次数为N*(N-1)/4。
移动次数：插入排序的移动次数与比较次数几乎一致，但移动的速度要比交换的速度快得多。

package practice1;

import java.util.Arrays;

public class InsertSort {
	public static void main(String[] args) {
		int[] a = {7, 6, 9, 8, 5,1 };
		insertSort(a);
		System.out.println(Arrays.toString(a));

	}

	public static void insertSort(int[] arr) {
		for (int i = 1; i < arr.length; i++) {
			int temp = arr[i];
			int leftIndex = i - 1;
			while (leftIndex >= 0 && arr[leftIndex] > temp) {
				arr[leftIndex + 1] = arr[leftIndex];
				leftIndex--;
			}
			arr[leftIndex + 1] = temp;
		}
	}
//	
}

4.快速排序

原理：在一串有序的数列中，我们总能找到一个处于中间或类似中间位置的数，在这个数一边的数比它大，另一边的数比它小。那么，在对无序数组排序的时候，我们能否找到这样的一个数，调整另外的数，让比它小的数居于一边，比它大的数居于一边，这样不就能达到排序的目的了吗？这就是快速排序的思想。

图解：在这里插入图片描述

public class QuickSort {
	//main方法的快捷键:main+alt+/+回车
	public static void main(String[] args) {
		int[] array = {7, 6, 9, 8, 5,1};
		System.out.println(Arrays.toString(quickSort(array,0,array.length-1)));
	
		
	}
	public static int[] quickSort(int a[], int start, int end) {// start是每次快速排序的数组开始下标，end是结束下标

		if (start > end) {
			return a;
		}
		int startNum = a[start];
		int left = start;// left是左标记的下标
		int right = end;// right是右标记的下标
		while (left != right)// 当左右标记没有相遇的时候
		{
			// 当左标记在右标记的左边并且右标记的数比左标记的数大时
			while (left < right && a[right] >= a[start]) {
				right--;// 右边标记左移
			}
			while (left < right && a[left] <= a[start]) {
				left++;// 左边标记右移
			}
			int temp = a[left];// 交换左边右边数的操作
			a[left] = a[right];
			a[right] = temp;
		}
		a[start] = a[left];// 将中间数交换到左右标记相遇的地方
		a[left] = startNum;

		quickSort(a, left + 1, end);// 对中间数左边的数组进行递归快速排序
		quickSort(a, start, right - 1);// 对中间数右边的数组进行递归快速排序

		return a;
	}
}