队列的基本描述，及c和c++分别顺序队列和链式队列实现，利用队列处理农夫过河问题

写在前面

：**
在开始前，请牢记这句话：队列是一个先进先出的数据结构。

即类似于通了水的水管一样的结构
定义：队列是一个线性的数据结构，规定这个数据结构只允许在一端进行插入，另一端进行删除，禁止直接访问除这两端以外的一切数据。
队列的用处
只要满足先来先服务特性的应用均可采用队列
作为其数据组织方式或中间数据结构
• 调度或缓冲
– 消息缓冲器
– 邮件缓冲器
– 计算机硬设备之间的通信也需要队列作为数据缓冲
– 操作系统的资源管理
• 宽度优先搜索
构造队列注意的问题：处理假溢出
队列主要操作：入队；出队；

一：队列的概述

队列是一个先进先出的数据结构，我们只能访问它的头和尾。
因此和构造栈是类似的：可数组构建也可链表构建。
（1）队列的构建
数组队列：
类似于这样利用数组和front下标和Rear下标即可构造出队列

链式队列
用单链表方式存储，队列中每个元素对应于链表中的一个结点。
链接指针的方向是从队列的前端向尾端链接

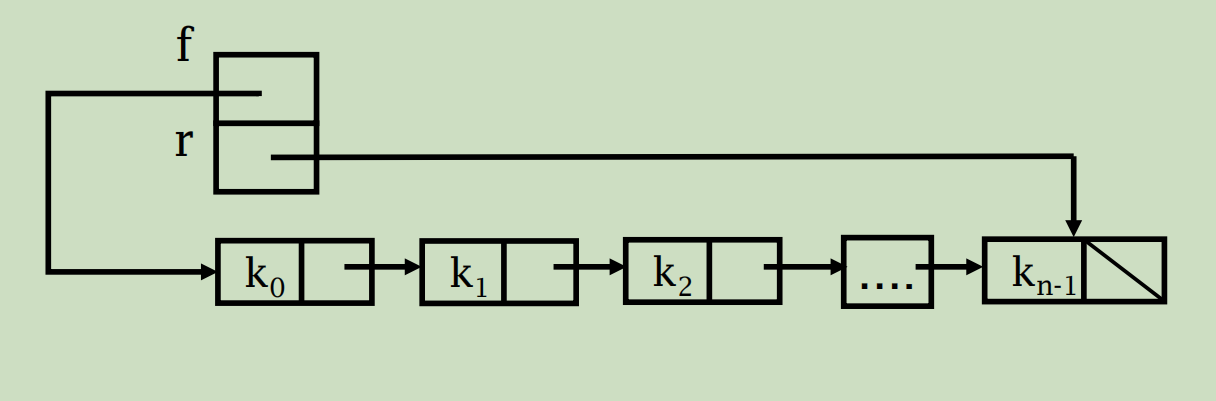
这样便可实现链式队列的数据成员了

两种方式的特点
顺序队列 被限制于固定的存储空间 但空间效率可以更高
链式队列 可以满足大小无法估计的情况
（2）队列的入队
入队:就是是从尾部添加一个元素
前提：只有在front 和 rear 之间的数组中的元素才是队列
那入队直接给Rear后移 然后此下标位置赋值即可
比如下面的这个 5,6入队。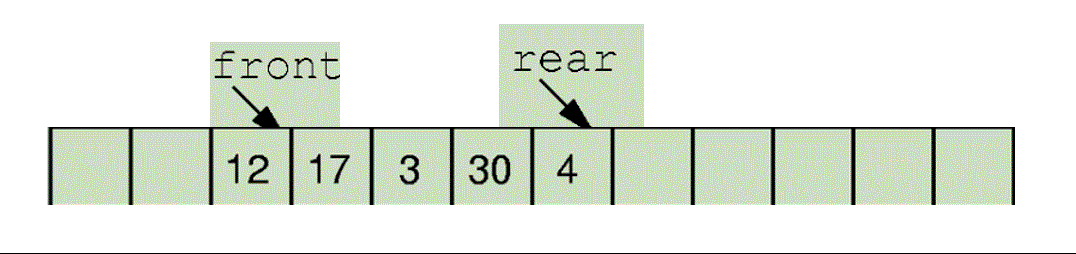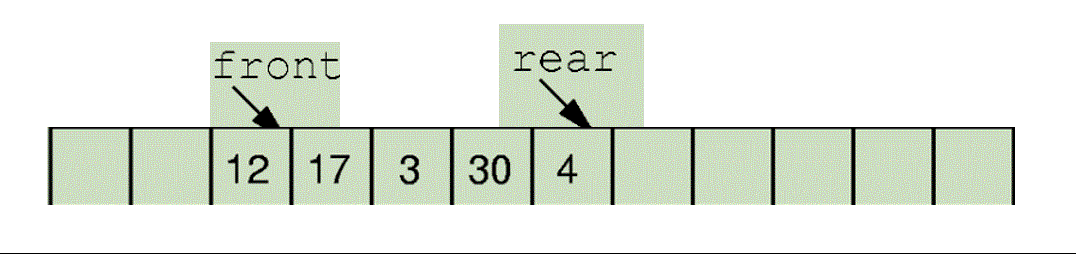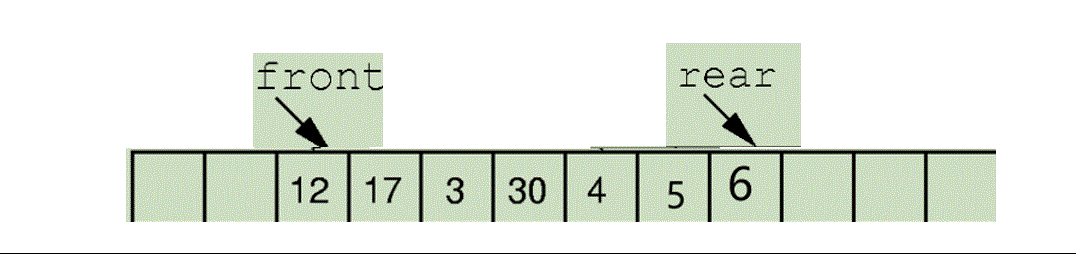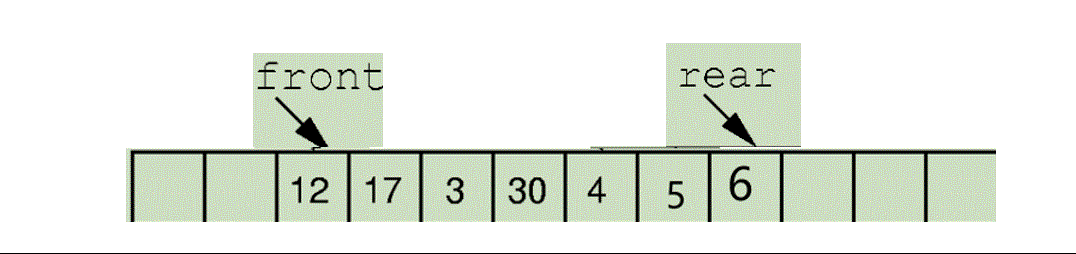
具体实现（这是循环队列（后面再介绍，多一步对capacity取余）的实现代码）
链式队列是由单链表实现的，那么很容易的想到尾插法（链表那章有介绍）
具体实现
（3）出队
队列出队 和栈出栈是类似的，出队和返回队列头元素是分开的。
顺序队列 直接把Front 往后移即可。
例如这里的 Data1 和Data2 出队

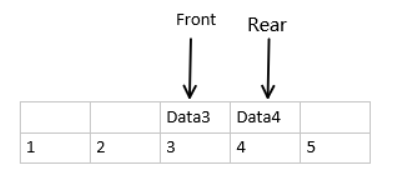
但是如果我们在这里 入队两个元素就会有假溢出

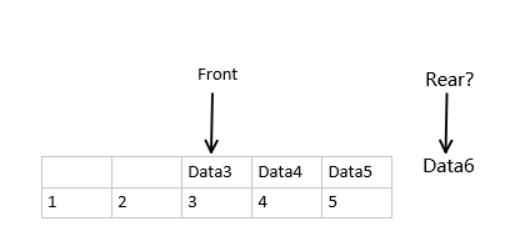
假溢出：顾名思义 还可以存元素，但却显示存满了。这是空间使用效率极低的，因此引入循环队列解决这个问题

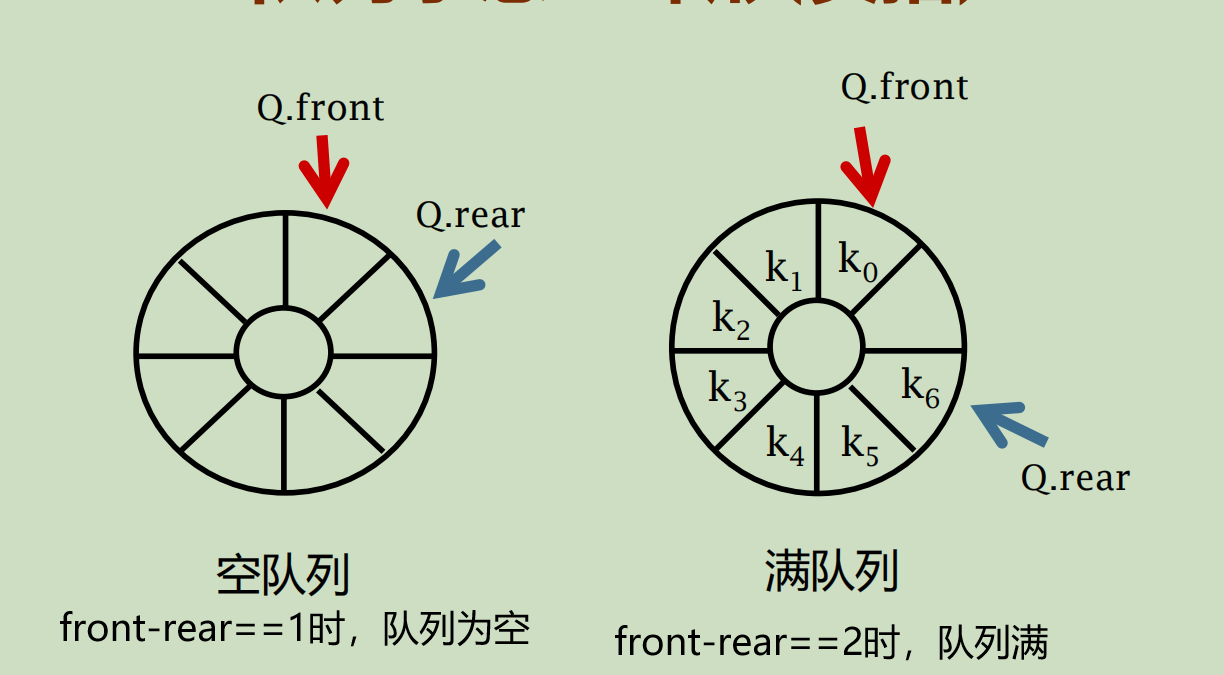
这是其中一种采用（front-rear）描述队列元素情况的方法（但是仍然有一个假溢出），还可以引入size和capacity来描述，此方法可以使数组真正存满
具体实现循环顺序队列出队

链式队列出队直接删掉头结点即可
链式队列 采用Rear ==nullptr 判断队列是否为空

（4）返回队头元素
顺序队列 直接返回front下标对应的元素即可

链式队列 返回头结点元素

（5）清空队列
顺序队列直接 对rear和size 和 front 重新赋值就好了

当然如果是删掉的话，还是要free的：
链式队列自然还是删链表

二.C实现顺序循环队列

    //顺序队列（没有假溢出）
#include<stdio.h>
#include<stdlib.h>
typedef int ElementType;
const int size = 100; //预留队列大小
typedef struct queue
{
    int Capacity; //队列的容量
    int Size;   //当前队列中存在的元素的个数
    int Rear;   //队尾 入队的位置
    int Front;  //队头 出队的位置     队列中只能操作这两个位置
    ElementType *Array; //顺序（数组实现）队列
} Queue;
int IsEmpty( Queue *Q ) //判断队列中是否有元素
{
    return Q->Size == 0;
}
int IsFull( Queue *Q ) //判断队列是否已经（满了）没有容量了
{
    return Q->Size == Q->Capacity;
}
void MakeEmpty(Queue *Q) //将队列制空（和顺序栈类似->通过改下标的方法）
{
    Q->Size = 0; //表明队列中无元素
    Q->Front = 1;   //回到起始位置（赋1是方面后面Rear先指向下一个元素）
    Q->Rear = 0; //尾赋为0
}
Queue *CreateQueue(unsigned int msize) //创建一个空队列
{
    Queue *Q = malloc(sizeof(Queue));
    if ( Q == NULL )  //检测下还有没有堆内存
        printf( "Error, out of space!!!" );
    Q->Array = malloc(sizeof(ElementType) * msize);
    if ( Q->Array == NULL )
        printf( "Error, out of space!!!" );
    Q->Capacity = msize; //容量就是开辟数组的大小
    MakeEmpty(Q);
    return Q;
}

void enQueue(Queue *Q, ElementType value)//入队
{
    if (IsFull(Q)) //队列满了则不能入队了
        printf("Error, full queue!" );
    else {
        ++Q->Size;
        Q->Rear = (Q->Rear + 1) % Q->Capacity; //因为是循环队列（一个环），所以对capacity取余
        Q->Array[Q->Rear] = value; //入队
    }
}
void deQueue(Queue *Q) //出队
{
    if (IsEmpty(Q)) //空队出不了队
        printf("Error, empty queue!");
    else {
        --Q->Size;
        Q->Front = (Q->Front + 1) % Q->Capacity; //front向后移就表明之前的元素出队了（它还在数组中但不在队列中）
    }
}
ElementType front(Queue *Q) //返回队头
{
    if (!IsEmpty(Q))
        return Q->Array[Q->Front]; //直接返回front下标元素
    printf("Error, empty queue!" );
    return 0;
}
ElementType deQueueAndFront(Queue *Q) //返回队头并出队
{
    if (!IsEmpty(Q)) {
        --Q->Size;
        ElementType temp = Q->Array[Q->Front]; //保留队头以便返回
        Q->Front = (Q->Front + 1) % Q->Capacity; //front后移（出队）
        return temp;
    }
    printf("Error, empty queue!" );
    return 0;
}
void disposeQueue( Queue *Q ) //free掉整个开辟的空间（包括队列外的元素）
{
    if ( Q != NULL )
    {
        free( Q->Array ); //从内到外 一层层free
        free( Q );
    }
}
int main()
{
    Queue *Q = CreateQueue(size);
    int i = 0;
    for (; i < 100; ++i) {
        enQueue(Q, i);
    }
    // for (i = 0; i < 101; ++i) {
    //     printf("%d ", deQueueAndFront(Q));
    // }
    for (i = 0; i < 101; ++i) {
        printf("%d ", front(Q));
        deQueue(Q);
    }
    printf("n");
    MakeEmpty(Q);
    for (i = 0; i < 10; ++i) {
        enQueue(Q, i);
    }
    for (i = 0; i < 10; ++i) {
        printf("%d ", front(Q));
        deQueue(Q);
    }
    disposeQueue(Q);
    return 0;
}

三。C++实现链式队列

#include<iostream>
using namespace std;
template <class T> class Link
{
public:
    T data; //用于保存结点元素的内容
    Link<T> *next; //指向后继结点的指针
    Link(const T info, Link<T> *nextValue = nullptr): data(info), next(nextValue) { }
    Link(Link<T> *nextValue = nullptr ): next(nextValue) {}
};
template <class T>
class Queue
{
public:
    Queue(void): front(nullptr), rear(nullptr) {} //空队列
    bool enQueue(T value); //入队
    bool deQueue(); // 返回队头元素并从队列中删除
    T deQueueAndFront();
    bool empty(); //清空队列
    T Front();
    ~Queue() { //析构
        empty();
    }
private:
    Link<T> *front; //队头
    Link<T> *rear;  //队尾
};
template <class T>
bool Queue<T>::enQueue(T value) //入队
{
    if (rear == nullptr) { //rear为空 意味着空队列
        rear = front = new Link<T>(value, nullptr); //空队列时，头和尾指向同一处
        return true;
    }
    rear = rear->next = new Link<T>(value, nullptr); //链表尾插法入队
    return true;
}
template <class T>
bool Queue<T>::deQueue() //队头出队
{
    if (rear == nullptr) { //空队没有元素出不了队
        cerr << "error,This is a blank queue!!!" << ends;
        return false;
    }
    auto deleted = front; //要delete的结点保留一下
    front = front->next; //front后移，之前的front便出队了
    delete deleted;  //delete
    if (front == nullptr)  //front为空，代表着未出队前只有队头，出队后无元素，rear要为nullptr
        rear = nullptr;
    return true;
}
template<class T>
T Queue<T>::Front() //返回队头元素
{
    if (rear == nullptr) {
        cerr << "error,This is a blank queue!!!" << ends;
        return T(0);
    }
    return front->data;
}
template<class T>
T Queue<T>::deQueueAndFront() //返回队头元素并将其出队
{
    if (rear == nullptr) { //空队没有元素出不了队
        cerr << "error,This is a blank queue!!!" << ends;
        return T(0);
    }
    auto deleted = front; //要delete的结点保留一下
    T temp = front->data;        //保留出队元素
    front = front->next; //front后移，之前的front便出队了
    delete deleted;  //delete
    if (front == nullptr)  //front为空，代表着未出队前只有队头，出队后无元素，rear要为nullptr
        rear = nullptr;
    return temp; //返回出队元素
}

template <class T>
bool Queue<T>::empty() //将整个队列清空
{
    while (front != nullptr) { //和删除一个单链表没有什么区别
        auto deleted = front;
        front = front->next;
        delete deleted;
    }
    return true;
}
int main()
{
    Queue<int> q;
    for (int i = 0; i < 1000; ++i) {
        q.enQueue(i);
    }
    for (int i = 0; i < 1001; ++i) {
        cout << q.deQueueAndFront() << ends;
    }
    q.empty();
    cout << endl;
    for (int i = 0; i < 1000; ++i) {
        q.enQueue(i);
    }
    for (int i = 0; i < 1000; ++i) {
        cout << q.deQueueAndFront() << ends;
    }
    return 0;
}

四：队列的应用之解决农夫过河

问题抽象**：“人狼羊菜”乘船过河**
– 只有人能撑船，船只有两个位置（包括人）
– 狼羊、羊菜不能在没有人时共处
问 ：人狼羊菜如何在安全的情况下从起始岸转移至对岸
1.问题抽象为模型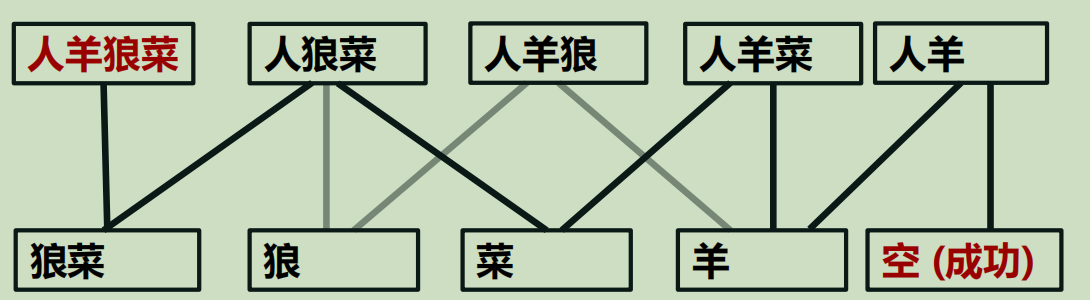
2.数据抽象
考虑到只有4个角色，并且只有两个状态（起始岸和对岸）
因此 可以设起始岸的角色对应于0 ，对岸的角色对应于1；

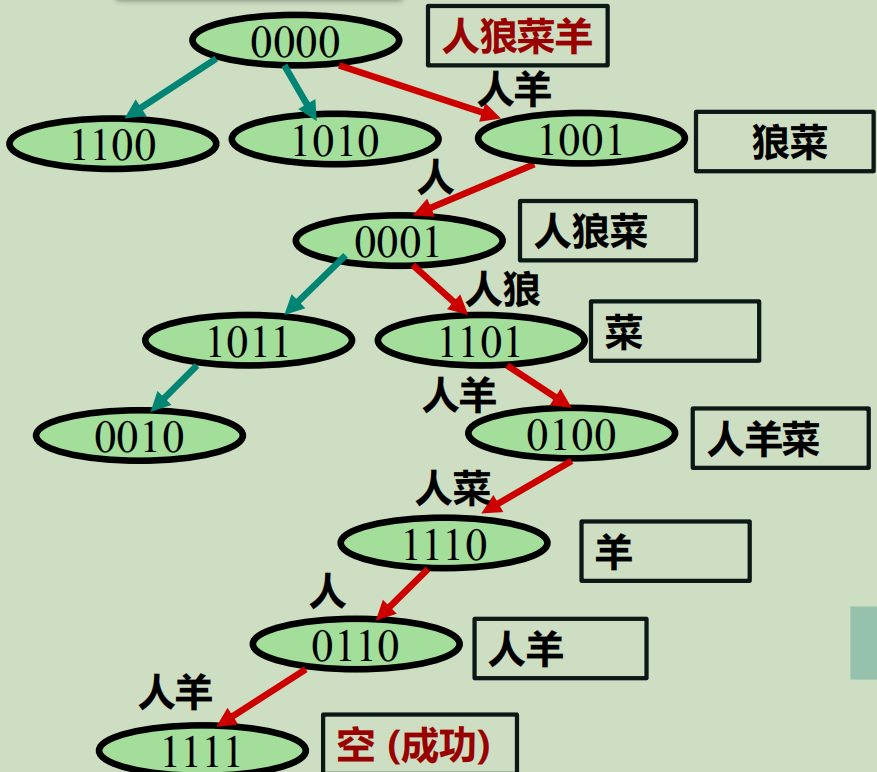
3.数据表示

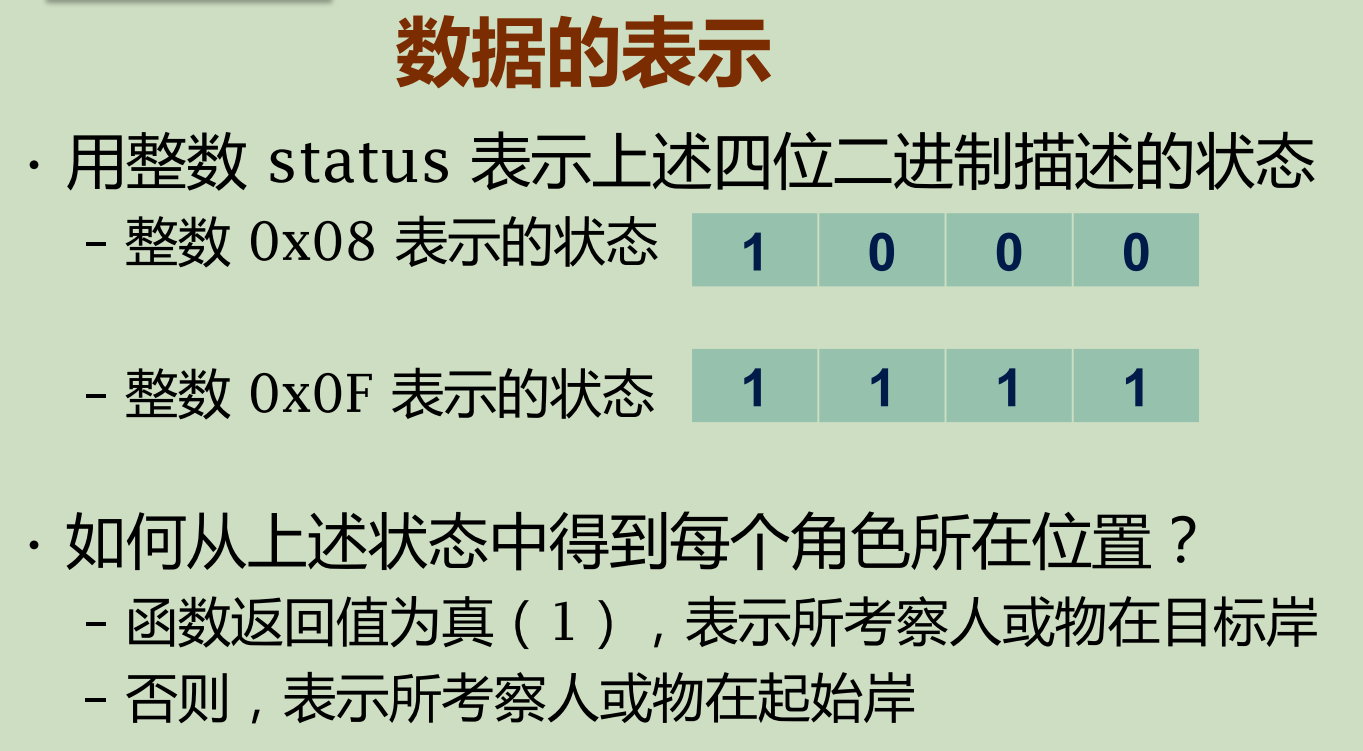
4.算法抽象：

5：算法设计

6.算法实现

//农夫过河问题
//  问题抽象：“人狼菜羊”乘船过河
// – 只有人能撑船，船只有两个位置（包括人）
// – 狼羊、羊菜不能在没有人时共处
//1.问题抽象为模型; 2.数据抽象 3.寻找合适的数据结构表示数据; 4算法抽象:0000->1111 5.算法设计 6.算法实现
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
//确定在   status状态下   每个角色的位置
//二进制表示   人 狼 菜 羊  返回 0表示在起始岸   1表示在对岸
bool farmer(unsigned int status) //1 x x x 人1   表明人在对岸
{
    return (status & 0x08) != 0; //&优先级比!=低，一定要加括号！
}
bool wolf(unsigned int status) //x 1 x x   狼1  表明狼在对岸
{
    return (status & 0x04) != 0;
}
bool cabbage(unsigned int status) //x x 1 x  菜1 表明菜在对岸
{
    return (status & 0x02) != 0;
}
bool goat(unsigned int status)  //x x x 1   羊1 表明羊在对岸
{
    return (status & 0x01) != 0;
}

bool safe(unsigned int status) //判断此状态是否安全
{
    if (goat(status) == cabbage(status) && goat(status) != farmer(status))
        return false; //羊草在一起且人不在  ，不安全
    if (goat(status) == wolf(status) &&  goat(status) != farmer(status))
        return false; //羊狼在一起且人不在，不安全
    return true; //其他状态安全
}
void solve()
{
    queue<unsigned int> move_to;
    // 每个元素表示一个可以安全到达的中间状态
    vector<int> route(16, -1);  //记录已被访问过的各个状态 值为-1代表未访问过，
    move_to.push(0x00); //初始状态，全部角色都在起始岸
    route[0] = 0x00;
    while (!move_to.empty() && route[15] == -1) {
        unsigned int status = move_to.front();
        //status代表着上一次过完河之后的状态 也就是现在的状态
        move_to.pop(); //出队
        for (unsigned int movers = 1; movers <= 8; movers <<= 1) { //4个角色对应的4种过河情况
            if (farmer(status) == bool(status & movers)) {
                //必须得和农夫一起（即同侧）才能过河。bool(&)表示要过河的这个角色在不在河对岸（status状态下）
                unsigned int newstatus = status ^ (0x08 | movers);   //改变status对应的farmer和movers的位置
                //异或是为了得到过河后的状态  ，|0x08是说明农夫带着一个东西 到了另一边(1与原状态异或一定改变)
                if (safe(newstatus) && route[newstatus] == -1) {
                    //如果这条路径安全，且未考虑过
                    route[newstatus] = status; //下一条路径就是下标，而上一条路径就是值；
                    move_to.push(newstatus); //保存安全的中间状态，以便下次while循环从这个状态开始继续向下寻找路径。
                }
            }
        }
    }
    // 反向打印出路径
    if (route[15] != -1) {
        cout << "The reverse path is : " << endl;
        for (int status = 15; status >= 0; status = route[status]) {// route[status]可以得到上一条路径
            //像递归一样返回去，找到所有路径
            cout << "The status is : " << status << endl;
            if (status == 0) break;
        }
    }
    else
        cout << "No solution." << endl;
}
int main()
{
    solve();
    return 0;
}

最后

以上就是畅快往事为你收集整理的队列的基本描述，及c和c++分别顺序队列和链式队列实现，利用队列处理农夫过河问题的全部内容，希望文章能够帮你解决队列的基本描述，及c和c++分别顺序队列和链式队列实现，利用队列处理农夫过河问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。