串的定义

串(string)是由零个或多个字符组成的有限序列，又名叫字符串。

一般定义为 S = “a1a2a3a4…an”; (n >= 0), ai（1<= i <= n)可以是字母，数字，或其他字符，i指的是该字符在串中的位置。

空串

零个字符的串称为“空串”，即 " null string"，可直接用双引号表示为“ “” ”。

空格串

只包含空格的串，和空串不同，空格串是有内容长度的，而且空格可以不止一个。示例：

s = "     ";

子串与真子串

若有串 “abcd”,则子串有：

a  b  c  d  ab  bc  cd  abc   bcd  abcd

即：4 + 3 + 2 + 1

那真子串为： 子串 - 1

子串与主串关系

主串中任意个数的连续字符组成的子序列称为该串的子串，相应地，包含字串的串称为主串。

子串在主串中的位置就是子串的第一个字符在主串中的序号。
例如：

"love"  是  "lover"  的子串

字符串匹配

输入为原字符串（string）和子串（pattern），要求返回子串在原字符串中首次出现的下标位置。
例如：
主串 “abcabcdabc”
子串 “abcd”
则返回下标3.

BF（朴素算法）

错误算法分析

利用两个指针指向主串与子串的开头， 让他们同时向后走，如果遇到相等的同时向后走；遇到不相等的，子串归零，再接着比较。

示例：

主串："abcabcdacb"
子串： "abcd"

在这个例子中，此方法可以找到子串，返回下标3。
但这是个特殊的串。大部分情况下此方法是错误的。
示例：

主串: "aaaaaaaaaab"
子串: "aaaaaaaab"

这个例子可以明显的看出子串可以和主串匹配，但是此算法却不行，
因为只让子串的指针回退，主串没有，所以当主串指针走到结尾时候还没有匹配成功，所以算法有缺陷。

正确BF解法

和上面的错误算法的差别就是：
指向主串的指针回退到哪里
如图，当两个指针同时向后走，遇到失配的时候，指向子串的指针（j)回退到0，那主串的指针( i )该回退到哪

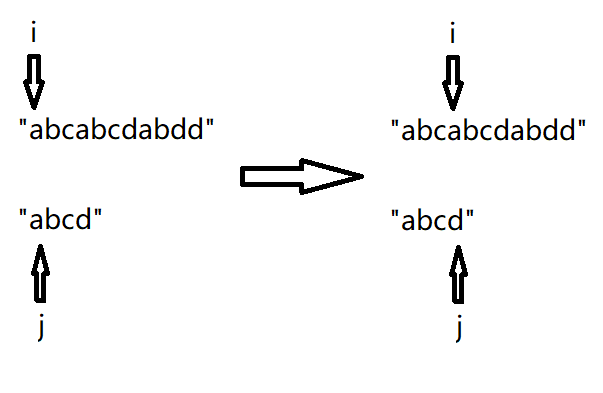
答案就是
(i)先回退到失配前的位置，再向后走一步，作为下一次匹配开始的位置。

那要怎么得来这个结果？

1. 先回到失配前的位置：即 i - j;
2. 再向后走一步作为下次匹配的开始： i - j + 1

其实就是暴力穷举法。。。

代码实现

其实就三步过程：

1. 两个指针同时向后跑
2. 如果相等，i++, j++
3. 如果不相等，回退： i = i - j + 1, j = 0

int BF_Search(const char *str, const char *sub, int pos)//(1)
{
	assert(str != NULL && sub != NULL && pos >= 0 && pos < strlen(str));
	if (str == NULL || sub == NULL || pos < 0 || pos >= strlen(str))
	{
		return -1;
	}

	int lenstr = strlen(str);//(2)
	int lensub = strlen(sub);//(3)
	int i = pos; //(4)
	int j = 0; //(5)

	while (i < lenstr && j < lensub)//(6)
	{
		if (str[i] == sub[j])//(7)
		{
			i++;
			j++;
		}
		else //(8)代表失配   
		{
			i = i - j + 1;
			j = 0;//这两行代码顺序不能反
		}
	}
	//此时while循环结束  则只有两种可能  你需要判断i和j谁走到了尾
	if(j >= lensub)//(9)
	{
		return i-j;//(10)
	}
	
	return -1; //(11)
}

1. 从主串的pos下标开始向后找字串
2. lenstr 保存主串的长度
3. lensub 保存字串的长度
4. i 保存主串匹配时的下标
5. j 保存子串匹配是的下标
6. 当主串和字串都没有走出范围的时候，循环继续
7. 如果相等 则i和j同时++， 判断下一个字符
8. 如果失配 则让i回退到这一次匹配前的位置的下一位 ，j归零
9. 如果指针j走到了尾巴 ，代表匹配成功了
10. 如果匹配成功 则返回这一次成功匹配前的位置
11. 如果字串j没走到尾，那代表主串没有字串想要的 则返回-1。

为什么从主串pos位置开始？
这种情况正常工作中也会用到，例如在查找在一堆文件中查找你想要的东西时，查找会根据你鼠标光标的位置。

示例：

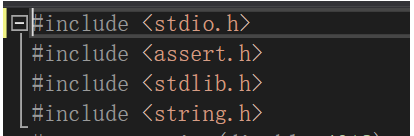
比如我现在光标在文档最开始位置，那我查找的话，如查找#include,第一个出现的就会亮起

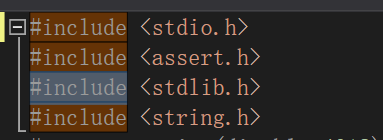
这次我将开始位置放到第三行再试试：

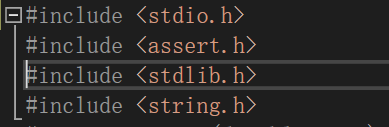
结果就是，第三行的#include亮起，因为我的pos位置发生了变化

测试

int main()
{
    const char *str = "ababcabcdabcde";//主串
	const char *sub = "abcd";
	int tmp = BF_Search(str, sub, 0);
	printf("tmp = %dn", tmp);
	tmp = BF_Search(str, sub, 7);
	printf("tmp2 = %dn", tmp);

	return 0;
}

运行结果

BF算法优缺点

优点：
简单，好实现
缺点：
时间复杂度很高，O(n * m)

所以需要想办法降低时间复杂度，就有下面的KMP算法。

KMP算法

特点：
主串不回退
时间复杂度O(n + m)

难点

1. 为什么主串指针 i 不回退
2. 子串指针 j 回退到哪个位置

失配情况

第一种情况：
发生失配情况时，子串前面的字符互不相等，示例：

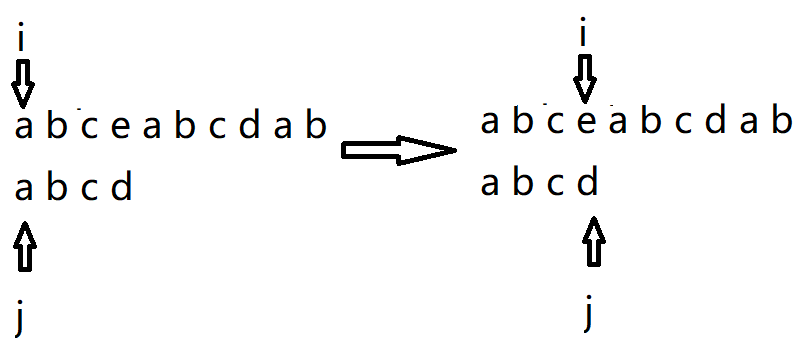
子串各个字符互不相等，则完全没有必要让 i 回退，因为回退也会失配。

第二种情况：

发生失配情况时，子串前面的字符有相等，如图中"ab", 并且是以头开始，以尾结束。

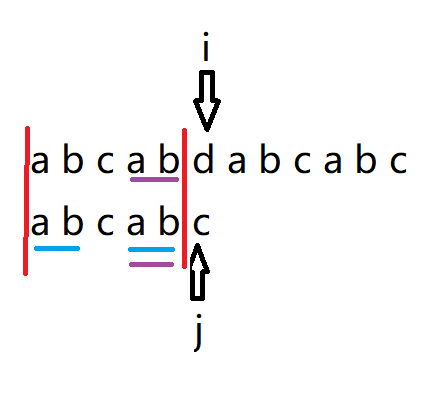
那 i 要回退到哪里？
如图：
因为主串回退到现在标记的前几个字符处是没有任何意义的，如图中的位置， a b是肯定会匹配成功的，所以此方法也不好。

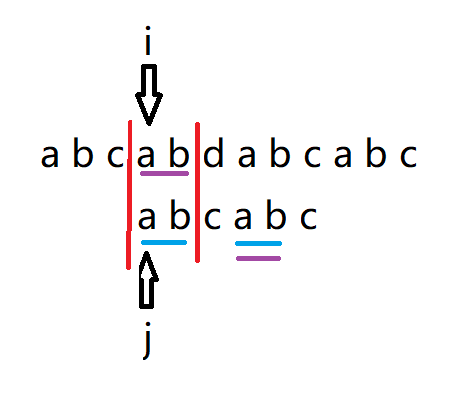
前面说到 主串 i 永不回退，那就要设法避免让i回退。

在上一步中，我们说让i 回退到图中紫色ab位置的a处， j 回退到初始位置，这样就让子串指针 j 回退到合适的位置，如图
这样避免了让 i 回退，而让 j 回退到合适的位置，这个合适的位置先记为 k。

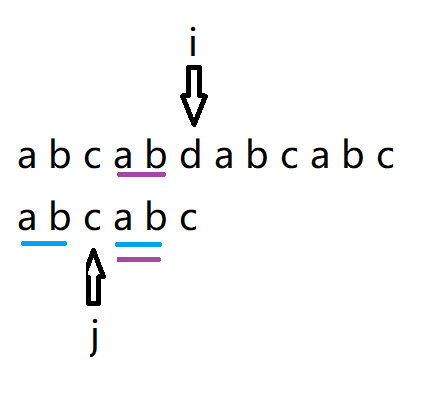
现在到了第二个难点，这个合适的位置K怎么求？

K:当失配时，j该回退的位置

每个位置都有可能失配，也就是说每个位置都得有一个合适的回退位置k。

那么我们需要一个表，来存放每个位置所需要回退的数，叫做部分匹配值表。

先看资料上的
部分匹配值表怎么产生？
首先要了解概念 “前缀” 和“后缀”。

前缀指除了最后一个字符以外，一个字符串的全部头部组合；
后缀指除了第一个字符以外，一个字符串的全部尾部组合。
示例：

next表就是“前缀”和“后缀”的最长的共有元素的长度，以"abcabd"为例：

• "a"的前缀和后缀都为空集，共有元素长度为0.
• "ab"的前缀为（a），后缀为（b），共有元素长度为0.
• "abc"的前缀为（a,ab），后缀为(bc,c),共有元素长度为0.
• “abca"的前缀为(a,ab,abc),后缀为(bca,ca,a)，共有元素为"a”，长度为1.
• “abcab"的前缀为(a,ab,abc,abca)，后缀为(bcab,cab,ab,b),共有元素为"ab”,长度为2.
• "abcabd"前缀为(a,ab,abc,abca,abcab)，后缀为(bcabd,cabd,abd,bd,d)，共有元素为0.

所以这个部分匹配值表为

部分匹配就是字符串头部和尾部会有重复。。

再看我老师讲的

把每个位置所需要回退的数，放到一个next数组中,还有硬性规定，示例：

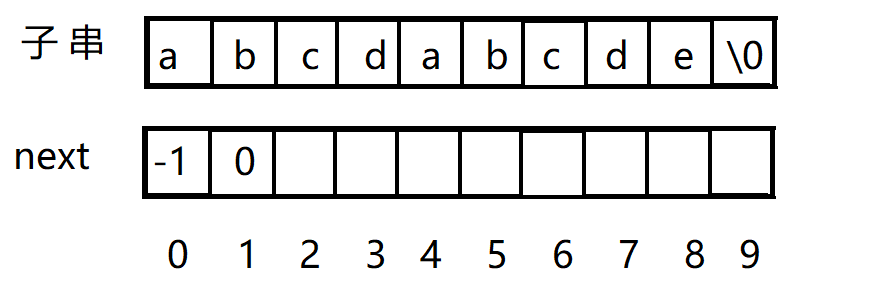
首先规定next数组的前两个元素为 -1 和 0。

k：发生失配的时候，向前看，看是否存在两个相等的最长真子串，一个位于头部，一个位于尾部顶着失配前的位置，就像上面有个例子中的"ab"。，那"ab"的长度就是k。

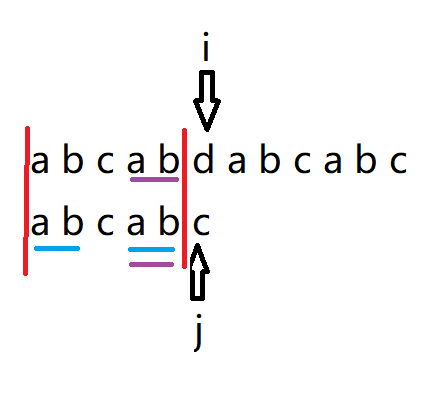
再上图失配处，"c"的next就是"ab"的长度 2。

懂了这一步，就先把老师讲的例子补全：

next数组例子

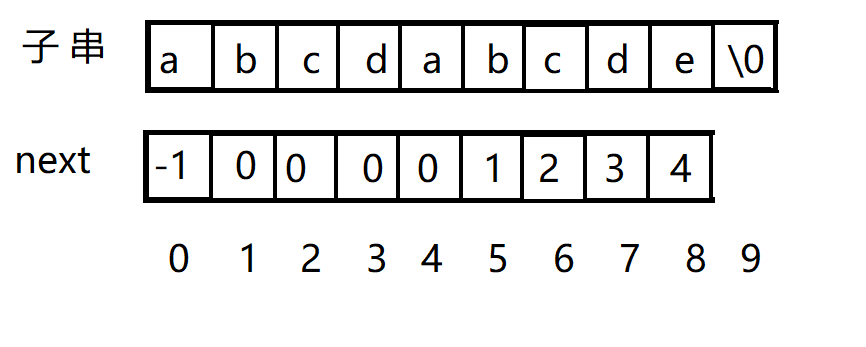
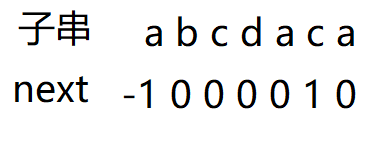
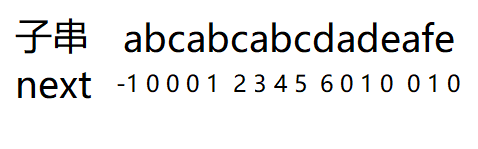
第二种方法：
利用已知推未知，像上面例子：

规定的前两个元素为 -1和 0.
子串中"c"的K值怎么求？
利用"b"的k值来推，做法是这样的：

当"b"失配时，回退位置是0号下标，那就判断和回退下标对应的字符（即"a"）是否相等，很显然不相等，那就把0给到"c"的K值。
后面步骤依次是这样，如果回退之后，和对应的字符相等，则 K++。

这样也能很容易把next数组写出来：

KMP代码实现

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<string.h>

int* Get_next(const char* sub)//next数组只跟子串有关
{
	int lensub = strlen(sub);//lensub保存子串的长度

	int* next = (int*)malloc(sizeof(int) * lensub);//申请一个等长的next数组来保存其每一个K值
	assert(next != NULL);

	next[0] = -1;//next数组的前两个空间有固定的值 -1 0
	next[1] = 0;

	int j = 1;//j保存的已知k的下标
	int k = 0;

	//通过已知推未知  j是已知  则j+1是未知   而j+1的合法性做判断（让j+1<lensub即可）
	while (j < lensub - 1)//给next数组每一个空间都赋合适的值  
	{
		if ((k == -1) || sub[j] == sub[k])//两个相等或者k回退到-1
		{
			next[++j] = ++k;
		}
		else
		{
			k = next[k];//k回退到合适的位置
		}
	}

	return next;//将malloc申请来的next数组返回出去
}

int KMP_Search(const char* str, const char* sub, int pos)//从主串的pos下标开始向后找字串
{
	assert(str != NULL && sub != NULL && pos >= 0 && pos < strlen(str));
	if (str == NULL || sub == NULL || pos < 0 || pos >= strlen(str))
	{
		return -1;
	}

	int lenstr = strlen(str);//lenstr 保存主串的长度
	int lensub = strlen(sub);//lensub 保存字串的长度
	int i = pos; //i 保存主串匹配时的下标
	int j = 0; //j 保存子串匹配时的下标

	int* next = Get_next(sub);//next数组只跟子串有关

	while (i < lenstr && j < lensub)//当主串和字串都没有走出范围的时候，循环继续
	{
		if ((j == -1) || str[i] == sub[j])//如果相等  则i和j同时++， 判断下一个字符
		{
			i++;
			j++;
		}
		else //如果失配  则让i回退到这一次匹配前的位置的下一位  而j归零
		{
			j = next[j];//j回到到合适的位置next[j]
		}
	}

	free(next);
	next = NULL;
	//此时while循环结束  则只有两种可能  你需要判断i和j谁走到了尾巴
	if (j >= lensub)//如果字串j走到了尾巴  代表匹配成功了
	{
		return i - j;//如果匹配成功  则返回这一次成功匹配前的位置
	}

	//如果字串j没走到尾巴  那代表主串没有字串想要的  则返回-1
	return -1;
}

代码基本和BF算法一致，就多了几步。。。。

为啥在while循环中的if判断还加了一步 j == -1 ?

因为失配的时候是通过next数组来给j的值的，有可能会把 -1给到 j，所以要加这一步。

测试

主函数：

int main()
{
	const char* str = "ababcabcdabcde";//主串
	const char* sub = "abcd";

	int tmp = KMP_Search(str, sub, 0);
	printf("tmp = %dn", tmp);
	tmp = KMP_Search(str, sub, 7);
	printf("tmp = %dn", tmp);

	return 0;
}

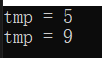
结果

小结

一定得会的知识：
1.主串i为什么死不回退
2.next数组只跟子串有关
3.给一个字符串，一定得会手写它的next数组的值
4.BF算法一定得会写

最后

以上就是害怕天空为你收集整理的基础数据结构-＞串-＞字符串匹配-＞BF和KMP算法串的定义字符串匹配的全部内容，希望文章能够帮你解决基础数据结构-＞串-＞字符串匹配-＞BF和KMP算法串的定义字符串匹配所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。