算法 (四) : 插入排序

69 阅读 0 评论 46 点赞

我是靠谱客的博主笨笨雨，最近开发中收集的这篇文章主要介绍算法 (四) : 插入排序，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

插入排序原理：它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

插入排序核心：假设第一个元素排好，之后的元素对排好的部分从后向前比较并逐一移动。

关键码

关键码是数据元素中某个数据项的值，用它可以标示一个数据元素。通常会用纪录来标示数据元素，一个纪录可以有若干数据项组成。例如，一个学生的信息就是一条纪录，它包括学号，姓名，性别等若干数据项。主关键码可以唯一的标示一个纪录的关键码，如学号。次关键码是可以标示若干记录的关键字，如性别、姓名。

假设一个文件有n跳纪录{}，对应的关键码是{}，排序家就是将此n个纪录按照关键码的大小递增（或递减）的次序排列起来，使这些纪录由无序变为有序的一种操作。排序后的序列若为{}时，其对应的关键码值满足{}或{}。

若在待排序的纪录中，存在两个或两个以上的关键码值相等的纪录，经排序后这些记录的相对次序仍然保持不变，则称相应的排序方法是稳定的方法，否则是不稳定的方法。

内部排序和外部排序

根据排序过程中涉及的存储器不同，可以讲排序方法分为两大类：一类是内部排序，指的是待排序的几率存放在计算机随机存储器中进行的排序过程；另一类的外部排序，指的是排序中要对外存储器进行访问的排序过程。

内部排序是排序的基础，在内部排序中，根据排序过程中所依据的原则可以将它们分为5类：插入排序、交换排序、选择排序、归并排序和基数排序；根据排序过程的时间复杂度来分，可以分为三类：简单排序、先进排序、基数排序。

评价排序算法优劣的标准主要是两条：一是算法的运算量，这主要是通过记录的比较次数和移动次数来反应；另一个是执行算法所需要的附加存储单元的的多少。

分类

包括：直接插入排序，二分插入排序（又称折半插入排序），链表插入排序，希尔排序（又称缩小增量排序）。属于稳定排序的一种（通俗地讲，就是两个相等的数不会交换位置）。

直接插入排序

直接插入排序是一种简单的插入排序法，其基本思想是：把待排序的纪录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的纪录插入完为止，得到一个新的有序序列。

例如,已知待排序的一组纪录是：

60,71,49,11,24,3,66

假设在排序过程中，前3个纪录已按关键码值递增的次序重新排列，构成一个有序序列：

49,60,71

将待排序纪录中的第4个纪录（即11）插入上述有序序列，以得到一个新的含4个纪录的有序序列。首先，应找到11的插入位置，再进行插入。可以讲11放入数组的第一个单元r[0]中，这个单元称为监视哨，然后从71起从右到左查找，11小于71，将71右移一个位置，11小于60，又将60右移一个位置，11小于49，又再将49右移一个位置，这时再将11与r[0]的值比较，11≧r[0]，它的插入位置就是r[1]。假设11大于第一个值r[1]。它的插入位置应该在r[1]和r[2]之间，由于60已经右移了，留出来的位置正好留给11.后面的纪录依照同样的方法逐个插入到该有序序列中。若纪录数n,续进行n-1趟排序，才能完成。

直接插入排序的算法思路：

（1）设置监视哨r[0]，将待插入纪录的值赋值给r[0]；

（2）设置开始查找的位置j；

（3）在数组中进行搜索，搜索中将第j个纪录后移，直至r[0].key≥r[j].key为止；

（4）将r[0]插入r[j+1]的位置上。

直接插入排序算法：

public void zjinsert(Redtyper[],int n)

{

int I,j;

Redtype temp;

for(i=1;i<n;i++)

{

temp= r[i];

j=i-1;

while(j>-1&&temp.key<r[j].key)

{

r[j+1]=r[j];

j--;

}

r[j+1]=temp;

}

稳定性

插入排序是在一个已经有序的小序列的基础上，一次插入一个元素。当然，刚开始这个有序的小序列只有1个元素，就是第一个元素。比较是从有序序列的末尾开始，也就是想要插入的元素和已经有序的最大者开始比起，如果比它大则直接插入在其后面，否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。

算法复杂度

如果目标是把n个元素的序列升序排列，那么采用插入排序存在最好情况和最坏情况。最好情况就是，序列已经是升序排列了，在这种情况下，需要进行的比较操作需（n-1）次即可。最坏情况就是，序列是降序排列，那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数加上(n-1）次。平均来说插入排序算法的时间复杂度为O(n^2）。因而，插入排序不适合对于数据量比较大的排序应用。但是，如果需要排序的数据量很小，例如，量级小于千，那么插入排序还是一个不错的选择。

折半插入排序（二分插入排序）

将直接插入排序中寻找A[i]的插入位置的方法改为采用折半比较，即可得到折半插入排序算法。在处理A[i]时，A[0]……A[i-1]已经按关键码值排好序。所谓折半比较，就是在插入A[i]时，取A[i-1/2]的关键码值与A[i]的关键码值进行比较，如果A[i]的关键码值小于A[i-1/2]的关键码值，则说明A[i]只能插入A[0]到A[i-1/2]之间，故可以在A[0]到A[i-1/2-1]之间继续使用折半比较；否则只能插入A[i-1/2]到A[i-1]之间，故可以在A[i-1/2+1]到A[i-1]之间继续使用折半比较。如此担负，直到最后能够确定插入的位置为止。一般在A[k]和A[r]之间采用折半，其中间结点为A[k+r/2]，经过一次比较即可排除一半纪录，把可能插入的区间减小了一半，故称为折半。执行折半插入排序的前提是文件纪录必须按顺序存储。

折半插入排序的算法思想：

算法的基本过程：

（1）计算0~i-1的中间点，用i索引处的元素与中间值进行比较，如果i索引处的元素大，说明要插入的这个元素应该在中间值和刚加入i索引之间，反之，就是在刚开始的位置到中间值的位置，这样很简单的完成了折半；

（2）在相应的半个范围里面找插入的位置时，不断的用（1）步骤缩小范围，不停的折半，范围依次缩小为1/21/41/8.......快速的确定出第i个元素要插在什么地方；

（3）确定位置之后，将整个序列后移，并将元素插入到相应位置。

3希尔排序法

希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数，把待排序文件中所有记录分成个组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工作。当到达=1时，所有记录在统一组内排好序。

各组内的排序通常采用直接插入法。由于开始时s的取值较大，每组内记录数较少，所以排序比较快。随着不断增大，每组内的记录数逐步增多，但由于已经按排好序，因此排序速度也比较快。

原理：

将n个元素的数列分为已有序和无序两个部分，如图所示：

{{a1}，{a2，a3，a4，…，an}}

{{a1⑴，a2⑴}，{a3⑴，a4⑴…，an⑴}}

…

{{a1(n-1），a2(n-1) ，…},{an(n-1)}}

每次处理就是将无序数列的第一个元素与有序数列的元素从后往前逐个进行比较，找出插入位置，将该元素插入到有序数列的合适位置中。

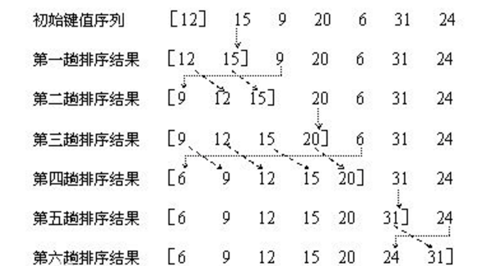
假设在一个无序的数组中，要将该数组中的数按插入排序的方法从小到大排序。假设啊a[]={3,5,2,1,4};插入排序的思想就是比大小，满足条件交换位置，一开始会像冒泡排序一样，但会比冒泡多一步就是交换后（a[i]=a[i+1]后）原位置（a[i]）会继续和前面的数比较满足条件交换，直到a[i+1]前面的数组是有序的。比如在第二次比较后数组变成a[]={2,3,5,1,4};