常用排序算法的python实现及优化

基础的排序

选择排序，冒泡排序，插入排序
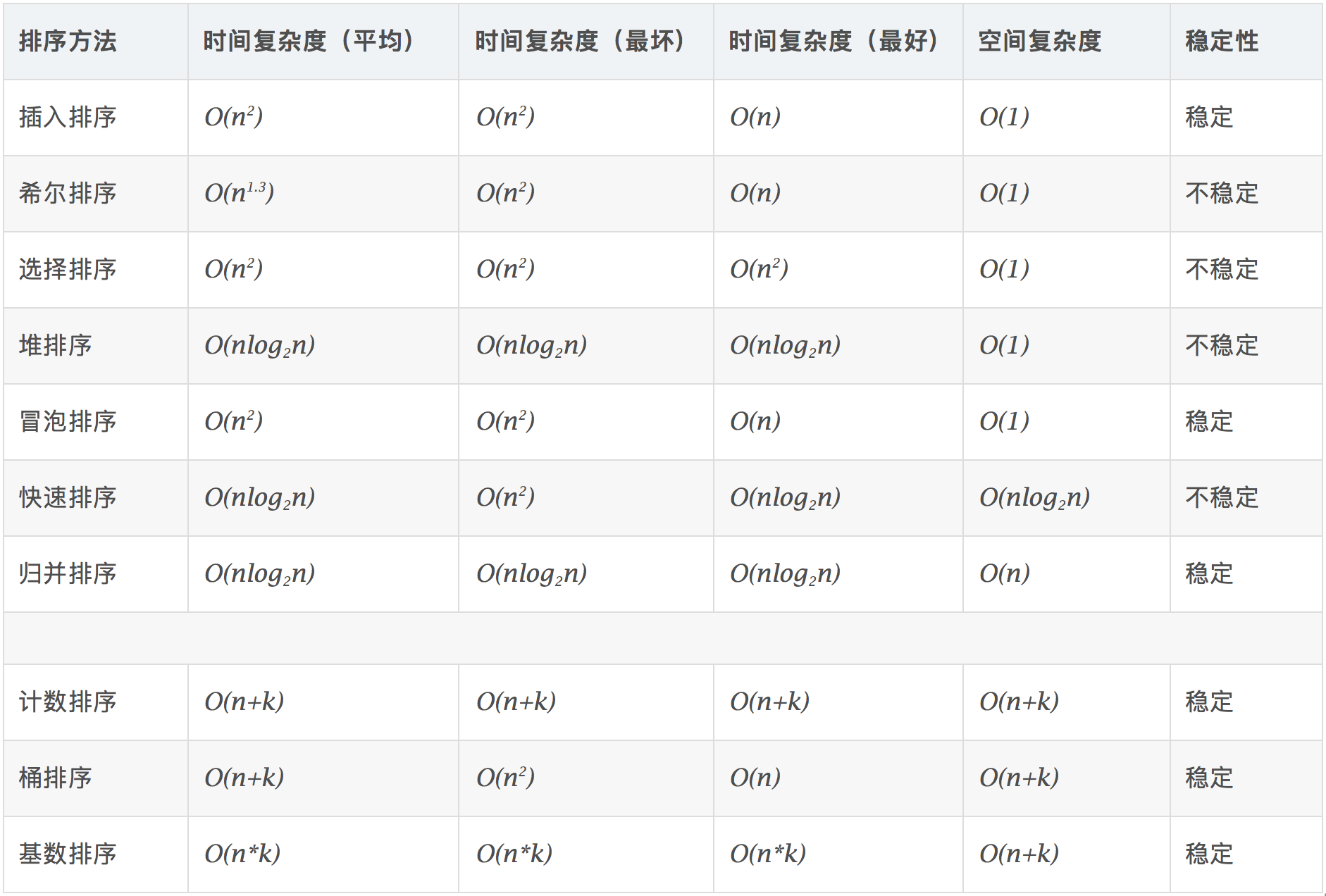
对于这三类排序主要考察基础，需要很熟悉的了解每种排序方法的时间复杂度，空间复杂度，以及稳定性。

（稳定是指如果数组里两个相等的数，排序前后这两个相等的数的相对位置保持不变）

同时要熟练掌握代码，将代码精炼，能在短时间内复现出无bug的代码。

选择排序

最简单直观的排序方法，每一趟都选择最小（最大）的元素，放到未排列的序列队首。每一趟会把一个最值放到正确位置。由于选择排序是交换最小元素与未排列序列的队首元素，所以是不稳定的排序方法。空间复杂度O(1)，时间复杂度O(n^2)。在数据规模小的时候使用方便。

python选择排序代码：

def sortArray(self, nums: List[int]):
	for i in range(len(nums)-1):
    	minindex=i
		for j in range(i+1,len(nums)):
            if nums[j]<nums[minindex]:
                minindex=j
        nums[i],nums[minindex]=nums[minindex],nums[i]
    return nums

冒泡排序

比较相邻元素的大小，如果第一个元素比第二个元素大就交换。然后移动到下一对。这样每遍历一趟就会有一个最大值被放到队尾。
空间复杂度：进行的操作是两两交换，所以空间复杂度为O（1）
时间复杂度：最好情况下进行n-1次比较，0次交换。最坏情况下进行n(n-1)/2次交换，复杂度O(n^2) 平均情况下时间复杂度O(n^2)
冒泡排序的时间复杂度是 O(n^2)。它是一种稳定的排序算法。

对原始的冒泡排序可以进行优化，如果进行一次遍历后没有发生交换，则数组已经排序完成。通过添加一个bool值判断是否发生交换即可。
python冒泡v1：

def sortArray(self, nums: List[int]):
    for i in range(1,len(nums)):
        issort=True
        for j in range(len(nums)-i):
            if nums[j]>nums[j+1]:
                nums[j],nums[j+1]=nums[j+1],nums[j]
                issort=False
        if issort:break
    return nums

假想一下如果一个列表只有前面几个数的顺序不对，后面多数的顺序都已经排列正确了。

比如 [4,3,2,1,5,6,7,8,9]

但是因为我们每次遍历都只把最大的一个数放到后面，这样就会将已经排列正确的后半数组比较很多次，由此我们可以进一步优化，找出已经排列正确的后半数组，只需要比较没有排列正确的数组即可。只需要添加一个数用来标记最后一次交换位置的下标即可。

冒泡排序v2：

def sortArray(self, nums: List[int]):
    n=len(nums)-1
    while n:
        issort=True
        for j in range(n):
            if nums[j]>nums[j+1]:
                nums[j],nums[j+1]=nums[j+1],nums[j]
                n=j
                issort=False
        if issort:break
    return nums

插入排序

从第一个元素开始，先把第一个元素看作已经排序好的，第二个到最后一个元素为未排序序列。未排序序列第一个元素跟已排序的前列元素进行比较，如果小于前列元素就交换位置，如此直到插入到合适的位置。插入排序经过每一轮的排序处理后，数组前端的数都是排好序的。

空间复杂度：进行的操作也是两两交换，复杂度O(1)
时间复杂度：最好情况下比较n-1次，不需要交换O(n)。最坏情况下进行n(n-1)/2次比较，复杂度O(n^2) 。插入排序的平均时间复杂度O(n^2)。也是一种稳定的排序。

python原始插入排序代码：

def sortArray(self, nums: List[int]):
    for i in range(1,len(nums)):
        for j in range(i,0,-1):
            if nums[j]<nums[j-1]:
                nums[j],nums[j-1]=nums[j-1],nums[j]
            else:break
    return nums

可以看到，原始的插入排序在每次插入的过程中都是与前一个元素进行比较，如果数据较大或者偏倒叙的情况下要进行多次比较。由此可以用二分查找的思想进行优化。

另一种对插入排序的优化就是希尔排序。

希尔排序

因为在插入排序中，在找到插入位置后要一个一个的把插入位置之后的元素都向后移动一位。所以这就会造成多次的移动。希尔排序优先比较距离较远的元素，把列表排列成一个整体有序的情况，在进行插入排序。所以希尔排序又叫缩小增量排序。

希尔排序的思想是先选取一组间隔，将整个序列分成若干组（相隔距离为间隔的元素为一组）。一般初始的间隔为数组长度的一半。先对组内进行插入排序。然后不停的缩小间隔，增加组内元素，直到间隔为1.

如果按照希尔排序的描述来构建代码，实际上是先根据间隔gap来分组，再在组内进行插入排序。这样的代码循环层数可能会比较多。
python希尔排序v1

def sortArray(self, nums: List[int]):
    n=len(nums)
    gap=n//2
    while gap:
        for i in range(gap):
            for j in range(i+gap,n,gap):
                for k in range(j,i,-gap):
                    if nums[k]<nums[k-gap]:
                        nums[k],nums[k-gap]=nums[k-gap],nums[k]
                    else:break
        gap//=2
    return nums

而通常写希尔排序的时候，并不是分组后再在组内进行插入排序的。仍然是从头到尾的对每个元素进行插入排序，只是在插入排序比较的时候比较的是相邻gap间隔的元素。这样的话就只需要在原来的插入排序的基础上添加一个间隔值gap的缩小循环即可。
python希尔排序v2

def sortArray(self, nums: List[int]):
    n=len(nums)
    gap=n//2
    while gap:
        for i in range(gap,n):
            j=i   #这里的j可以直接用i表示，但是因为下一个循环中i的值会变化，为了方便理解取了个新值j
            while j-gap>=0 and nums[j]<nums[j-gap]:
                nums[j],nums[j-gap]=nums[j-gap],nums[j]
                j-=gap
        gap//=2
    return nums

归并排序

采用的是分治的思想，把数组分为子数组，对子数组实现排序后再合并。通常情况下对数组做二分。归并排序时间复杂度为O(nlogn)，但是需要额外的空间，空间复杂度为O(n).归并排序是稳定的排序。

python归并排序：

class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        if len(nums)<=1:
            return nums
        mid=len(nums)//2
        left=self.sortArray(nums[:mid])
        right=self.sortArray(nums[mid:])
        return merge(left,right)

    def merge(left,right):
        res=[]
        while left and right:
            if left[0]<=right[0]:
                res.append(left.pop(0))
            else:
                res.appen(right.pop(0))
        res=res+left+right
        return res
            

快速排序

最常考察的排序方法，同样使用到了分治的思想。快速排序的思想是从数组中选取一个值作为基值，以基值为分界点将整个数组划分为两个子数组。在基值前面的数组的值都比基值小，后面的都比基值大。然后再递归的对子数组使用相同的划分。实际中基值的选择通常选择第一个数，为了防止最坏情况的发生（即倒序），可以在排序前先将数组进行打乱。

python快速排序：

def sortArray(self, nums):
    if len(nums)<=1:
        return nums
    left=0
    right=len(nums)-1
    pivot=nums[0]
    while left<right:
        while left<right and nums[right]>=pivot:
            right-=1
        while left<right and nums[left]<=pivot:
            left+=1
        nums[left],nums[right]=nums[right],nums[left]
    nums[0],nums[left] =nums[left],pivot
    res=[]
    res=res+self.sortArray(nums[:left])
    res.append(pivot)
    res=res+self.sortArray(nums[left+1:])
    return res

堆排序

堆排序用构建大顶堆（小顶堆）的方法，先将数组构从底向上建成一个堆。然后每次将堆顶的元素与尾部元素交换。这样尾部元素就是最大值了。再将剩下的元素从头开始交换，推出第二个顶堆。以此迭代
python堆排序：

class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        def comp(i,n):
            l=2*i+1
            r=2*i+2
            larger=i
            if l<n and nums[l]>nums[larger]:
                larger=l
            if r<n and nums[r]>nums[larger]:
                larger=r
            if larger!=i:
                nums[i],nums[larger]=nums[larger],nums[i]
                comp(larger,n)
        n=len(nums)
        node=n//2-1
        for i in range(node,-1,-1):
            comp(i,n)
        while n:
            nums[0],nums[n-1]=nums[n-1],nums[0]
            n-=1
            node=n//2-1
            comp(0,n)
        return nums

最后

以上就是柔弱小笼包为你收集整理的常用排序算法的python实现及优化的全部内容，希望文章能够帮你解决常用排序算法的python实现及优化所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。