目录

插入排序

1.1 直接插入

1.1.1思路

1.1.2例子

1.1.3 复杂度和稳定性分析

1.1.4 java代码

1.2折半插入排序

1.2.1思路

1.2.2例子

1.2.3 复杂度和稳定性分析

1.2.4 java代码

1.3shell排序

1.3.1思路

1.3.2例子

1.3.3 复杂度和稳定性分析

1.3.4 java代码

插入排序

1.1 直接插入

1.1.1思路

每次从无序表中取出第一个元素，把它插入到有序表的合适位置，使有序表仍然有序。

即：当插入第i个元素(i >= 1)时，前面的V[0]，V[1]，……，V[i-1]已经排好序。这时，用V[i]的排序码与V[i-1]，…，V[1]，V[0]的排序码顺序进行比较，找到插入位置即将V[i]插入，原来位置上的元素向后顺移。

1.1.2例子

例一：各趟排序过程

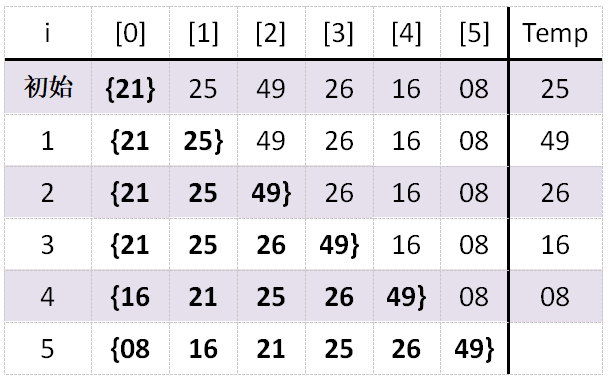
例二：一趟排序过程，i=3时

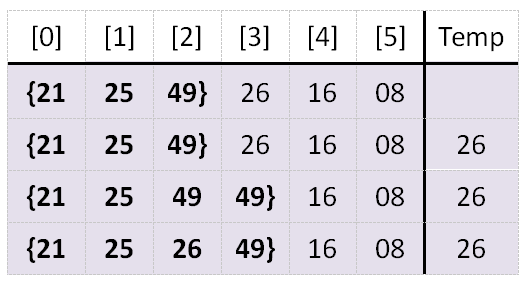
1.1.3 复杂度和稳定性分析

空间上看：

它只需要一个辅助空间temp ，因此其空间复杂度位O(1)。

时间上看：

当最好的情况下，也就是序列本身就是有序的 ，这个时候我们只需比较n-1，无需移动即可。这个时候时间复杂度为O(n)。

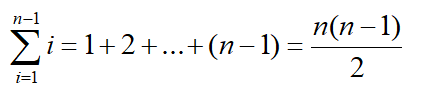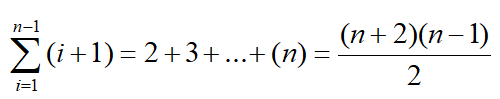当最坏的情况下，也就是序列本身是逆序的 ，这个时候我们需比较，移动。这个时候时间复杂度为。因此平均时间复杂度为。

稳定性：

假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。

因此是稳定的。

1.1.4 java代码

 private void insertSort(int[] a) {
        int n = a.length;
        int i,j;
        for(i=1;i<n;i++){
            /**
             * temp为本次循环待插入有序列表中的数
             */
            int temp = a[i];
            /**
             * 寻找temp插入有序列表的正确位置
             */
            for(j=i-1;j>=0 && a[j]>temp;j--){
                /**
                 * 元素后移，为插入temp做准备
                 */
                a[j+1] = a[j];
            }
            /**
             * 插入temp
             */
            a[j+1] = temp;
        }
    }

1.2折半插入排序

1.2.1思路

基本思想和直接插入排序相同，不同在于查找插入位置。直接插入排序是采用顺序查找法，而折半插入排序排序是采用二分查找思想。

1.2.2例子

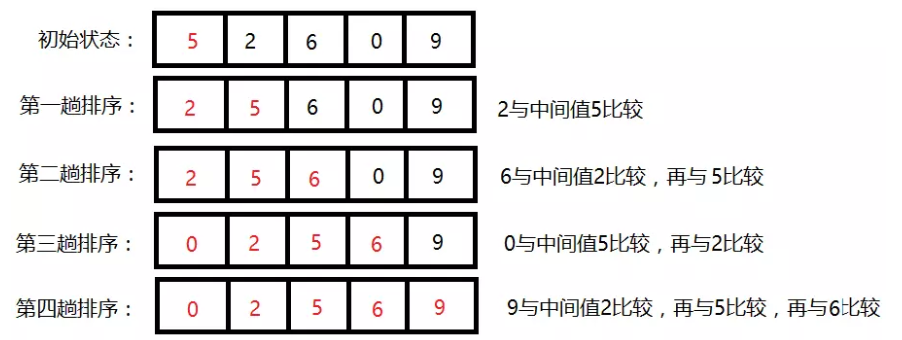
1.2.3 复杂度和稳定性分析

空间上看：

它只需要一个辅助空间temp ，因此其空间复杂度位O(1)。

时间上看：

折半插入排序减少了比较元素的次数，约为O(nlogn)，比较的次数取决于表的元素个数n。因此，折半插入排序的时间复杂度仍然为O(n²)，但它的效果还是比直接插入排序要好。

稳定性：

假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。

因此是稳定的。

1.2.4 java代码

private void binaryInsertSort(int[] a) {
        int n = a.length;
        int i,j;
        for(i=1;i<n;i++){
            /**
             * temp为本次循环待插入有序列表中的数
             */
            int temp = a[i];
            int low=0;
            int high=i-1;
            /**
             * 寻找temp插入有序列表的正确位置，使用二分查找法
             */
            while(low <= high){
                /**
                 * 有序数组的中间坐标，此时用于二分查找，减少查找次数
                 */
                int mid = (low+high)/2;
                /**
                 * 若有序数组的中间元素大于待排序元素，则有序序列向中间元素之前搜索，否则向后搜索 
                 */
                if(a[mid]>temp){
                    high = mid-1;
                }else{
                    low = mid+1;
                }
            }
            
            for(j=i-1;j>=low;j--){
                /**
                 * 元素后移，为插入temp做准备
                 */
                a[j+1] = a[j];
            }
            /**
             * 插入temp
             */
            a[low] = temp;
          }
     }

1.3shell排序

1.3.1思路

希尔排序(Shell's Sort)又称“缩小增量排序”（Diminishing Increment Sort）。先将整个待排记录序列分割成若干个子序列，分别进行直接插入排序，待整个序列中的记录 “基本有序” 时，再对全体记录进行一次直接插入排序。该方法实质上是一种分组插入方法。

1.3.2例子

用一个变量dk = 5 ,将全部序列分割成

这里要做的事将a[0] ,a[5] ,a[10]；a[1] ,a[6] ,a[11] ；a[2] ,a[7] ,a[12]；a[3] ,a[8]...这几组数做直接插入排序，注意此时的间隔为5，而不是之前的1，完成后

发现规律 ，只要是间隔5的每一组数都是有序的，如{35，41，81}，{17,75,91}，{11,15,95}都是有序的，这也导致了全部的序列有序性有所提高。

继续我们现在另dk = 3 ，即将上面的序列分割成间隔为3的子序列，看颜色区分

同理按照5间隔的规则进行排序，排序完后

这个时候有序性又提高了不少。最后再将所有的序列做最后一次的直接插入排序，dk = 1的排序。

直接插入排序在序列元素少，序列的有序性好的情况下，它的效率是非常高的。

这个时候就已经全部排序完成了。

1.3.3 复杂度和稳定性分析

空间上看：

它只需要一个辅助空间temp ，因此其空间复杂度位O(1)。

时间上看：

希尔排序的运行时间依赖于增量序列的选择。

使用希尔增量时希尔排序的最坏情形运行时间为θ(N2)。

Hibbard增量序列：1,4,7,…,2k-1。这个增量的特点是增量没有公因子

使用Hibbard增量的希尔排序的最坏情形运行时间为θ(N3/2)。

希尔排序没有快速排序算法快 O(n(logn))，因此中等大小规模表现良好，对规模非常大的数据排序不是最优选择。但是比O(

)复杂度的算法快得多。并且希尔排序非常容易实现，算法代码短而简单。 此外，希尔算法在最坏的情况下和平均情况下执行效率相差不是很多，与此同时快速排序在最坏的情况下执行的效率会非常差。几乎任何排序工作在开始时都可以用希尔排序，若在实际使用中证明它不够快，再改成快速排序这样更高级的排序算法。

稳定性：

假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。

因此是稳定的。

1.3.4 java代码

private void shellSort(int[] a){
        int n=a.length;
        int gap=n/2;
        while(gap>=1){
            for(int i=gap;i<a.length;i++){
                int j=0;
                int temp = a[i];
                for(j=i-gap;j>=0 && temp<a[j];j=j-gap){
                    a[j+gap] = a[j];
                }
                a[j+gap] = temp;
            }
            printResult(a,a.length);
            gap = gap/2;
        }
}

最后

以上就是自觉太阳最近收集整理的关于排序算法——插入排序插入排序的全部内容，更多相关排序算法——插入排序插入排序内容请搜索靠谱客的其他文章。