【数据结构】内部排序- -交换排序小结（冒泡排序、快速排序）

1 冒泡排序

1.1 思想：

（BubbleSort）像小鱼吐泡泡一样，吐出后飘呀飘，泡泡慢慢变大。从后往前（或者从前往后）两两比较，只要较小元素，然后接着比，最后结果就是最小元素冒到最前面（最大元素冒到最后面），第一趟结束。至多n - 1 趟就能排好所有元素。若某趟结束后没得交换，说明已经有序，冒泡结束。

• 冒泡排序产生的有序子列在全局中仍是有序的。也就是说，一趟都至少能确定一个元素的最终位置。
• 过程如下
  

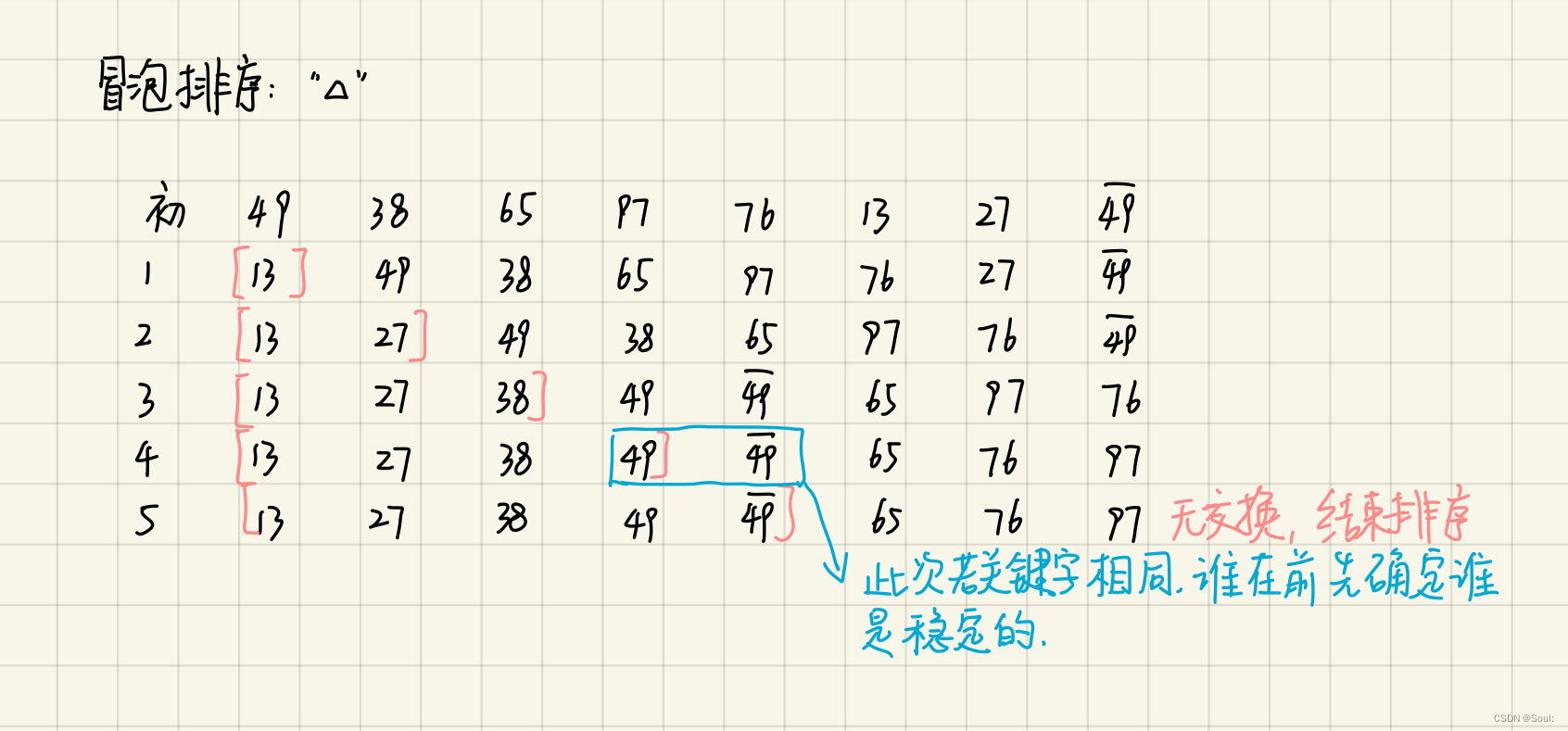
1.2 算法分析

• 稳定性：稳定
• 空间复杂度：O（1）
• 与初态是否有关：有关
• 顺序存储 + 链表结构
• 时间复杂度：
  最好时间复杂度：O（n）
  最坏时间复杂度：O（ n^2）
  平均时间复杂度：O（n^2）

关于时间复杂度：最好的情况就是初始序列正序，此时只需比较 n - 1 次，无须移动，时间复杂度O（n）；最坏的情况就是初始序列逆序，既要比较又要移动元素。

1.3 代码

//这里是冒泡排序
void BubbleSort(ElemType A[],int n)
{
    for(int i = 0; i<n-1;i++)//从后往前两两比较相邻元素的值，进行n-1趟
    {
        flag=false;//设置标志位，因为当未发生元素交换，即标志位未变，说明序列已有序，冒泡结束。
        for(j=n-1;j>i;j--)//一趟冒泡排序，下标从0开始，n-1为止，因此for循环从n-1开始。
        {
            if(A[j-1]>A[j]//将小元素冒到前面，若前面的比后面大，交换。
            {
               swap(A[j-1],A[j]);
               flag=true;//发生了交换，序列还未有序
            }
        }
        if(flag == false)
             return 0;
    }
}

2 快速排序

2.1 思想

使用 low、high、pivot 三个指针，从两头向中间按一定规则靠拢，以pivot 作为基准(又称枢轴)，得到这样的结果：pivot左边是小于基准的元素，右边是大于基准的元素。

• 快排是所有内部排序算法中平均性能最吊的；
• 快排基于分治法，是一个交替搜索和交换的过程；
• 关键是在于划分，也直接关系到算法性能；
• 是递归的，其时间复杂度和空间复杂度也与递归调用的深度一致；（树的深度）
• 最终将基准元素放到应在的位置，不产生有序子序列；
• 越乱性能越优，正序逆序反而性能很差；
• 排序过程如下：
  
  

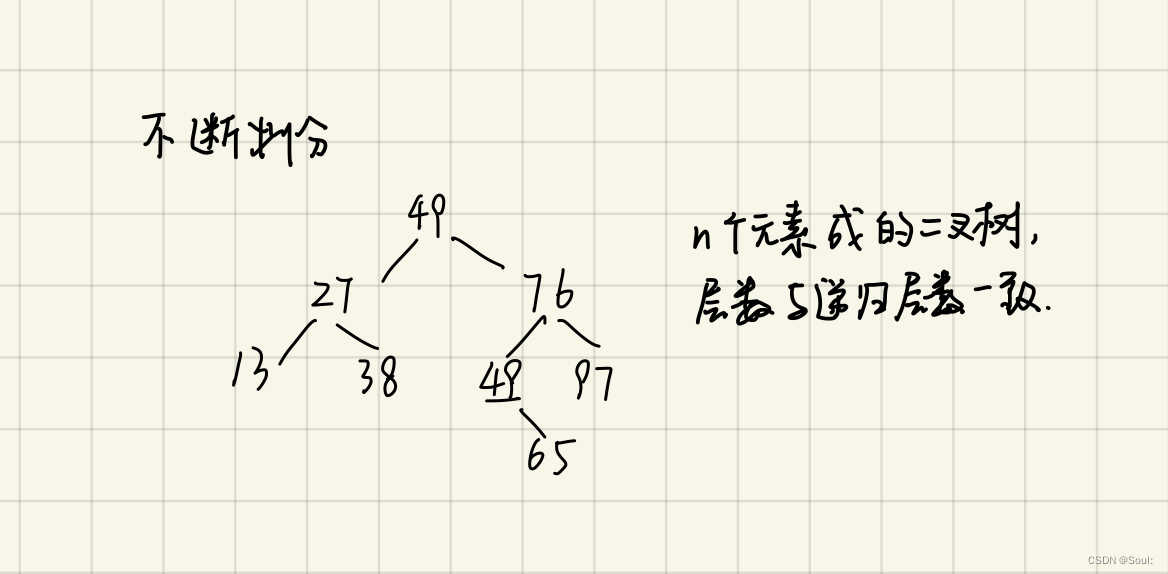
2.2 算法分析

• 稳定性：不稳定
• 空间复杂度：O（log n）
• 与初态是否有关：有关
• 顺序存储，不宜使用链表
• 时间复杂度：
  最好时间复杂度：O（n log n）
  最坏时间复杂度：O（ n^2）
  平均时间复杂度：O（n log n）

2.3 代码

//快速排序
//将第一个元素作为基准，把待排序列划分左右两个部分
int Partition (ElemType A[], int low, int high)
{
	ElemType pivot = A[low];// 将第一个元素作为枢轴，存储起来，防止覆盖
	while(low < high)
    {
    	while(low < high && A[high] >= pivot)
    	//从最右边开始，依次比较基准和A[high]的值，直至基准元素大时，交替左侧；
    		- -high;//先取值，再 —1
         A[low] = A[high];
        while (low < high && A[low] <= pivot)
        //从最左边开始，依次比较基准和A[low]的值，直至基准元素小时，交替右侧；
            ++low;//先取值，再 +1
         A[high] = A[low];
     }
    A[low] = pivot;//low 与 high 的值相同，正是基准元素应该在的位置
    return low;
}

void QuickSort(ElemType A[],int low, int high)
{
	if( low < high)
   {
   		int pivotpots = Partition( A, low，high);
   		QuickSort(A, low, pivotpots-1);//划分左子表
    	QuickSort(A, pivotpots+1, high);
   }
}

最后

以上就是坦率保温杯为你收集整理的【数据结构】内部排序- -交换排序小结（冒泡排序、快速排序）的全部内容，希望文章能够帮你解决【数据结构】内部排序- -交换排序小结（冒泡排序、快速排序）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。