啥是拓扑排序?
一个有向图,如果图中有入度为 0 的点,就把这个点删掉,同时也删掉这个点所连的边。
一直进行上面出处理,如果所有点都能被删掉,则这个图可以进行拓扑排序。
举例子
开始时,图是这样的状态,发现A的入度为 0,所以删除A和A上所连的边,结果如下图:
这时发现B的入度为 0,C的入度为 0,所以删除B和B上所连的边、C和C上所连的边,结果如下图:
这时发现发现D的入度为 0,所以删除D和D上所连的边(如果有就删),结果如下图:
这时整个图被删除干净,所有能进行拓扑排序。
解题思路
首先记录各个点的入度
然后将入度为 0 的点放入队列
将队列里的点依次出队列,然后找出所有出队列这个点发出的边,删除边,同事边的另一侧的点的入度 -1。
如果所有点都进过队列,则可以拓扑排序,输出所有顶点。否则输出-1,代表不可以进行拓扑排序。
#include
#include
#include
using namespace std;
const int N = 100010;
int e[N], ne[N], idx;//邻接矩阵存储图
int h[N];
int q[N], hh = 0, tt = -1;//队列保存入度为0的点,也就是能够输出的点,
int n, m;//保存图的点数和边数
int d[N];保存各个点的入度
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void topsort(){
for(int i = 1; i <= n; i++){//遍历一遍顶点的入度。
if(d[i] == 0)//如果入度为 0, 则可以入队列
q[++tt] = i;
}
while(tt >= hh){//循环处理队列中点的
int a = q[hh++];
for(int i = h[a]; i != -1; i = ne[i]){//循环删除 a 发出的边
int b = e[i];//a 有一条边指向b
d[b]–;//删除边后,b的入度减1
if(d[b] == 0)//如果b的入度减为 0,则 b 可以输出,入队列
q[++tt] = b;
}
}
if(tt == n - 1){//如果队列中的点的个数与图中点的个数相同,则可以进行拓扑排序
for(int i = 0; i < n; i++){//队列中保存了所有入度为0的点,依次输出
cout << q[i] << " ";
}
}
else//如果队列中的点的个数与图中点的个数不相同,则可以进行拓扑排序
cout << -1;//输出-1,代表错误
}
int main(){
cin >> n >> m;//保存点的个数和边的个数
memset(h, -1, sizeof h);//初始化邻接矩阵
while (m – ){//依次读入边
int a, b;
cin >> a >> b;
d[b]++;//顶点b的入度+1
add(a, b);//添加到邻接矩阵
}
topsort();//进行拓扑排序
return 0;
}
拓扑排序
只适用于 AOV网 (有向无环图)
算法流程:
用队列来执行 ,初始化讲所有入度为0的顶点入队。
主要由以下两步循环执行,直到不存在入度为 0 的顶点为止
选择一个入度为 0 的顶点,并将它输出;
删除图中从顶点连出的所有边。
循环结束,
若输出的顶点数小于图中的顶点数,则表示该图存在回路,即无法拓扑排序,
否则,输出的就是拓扑序列 (不唯一)
模板题
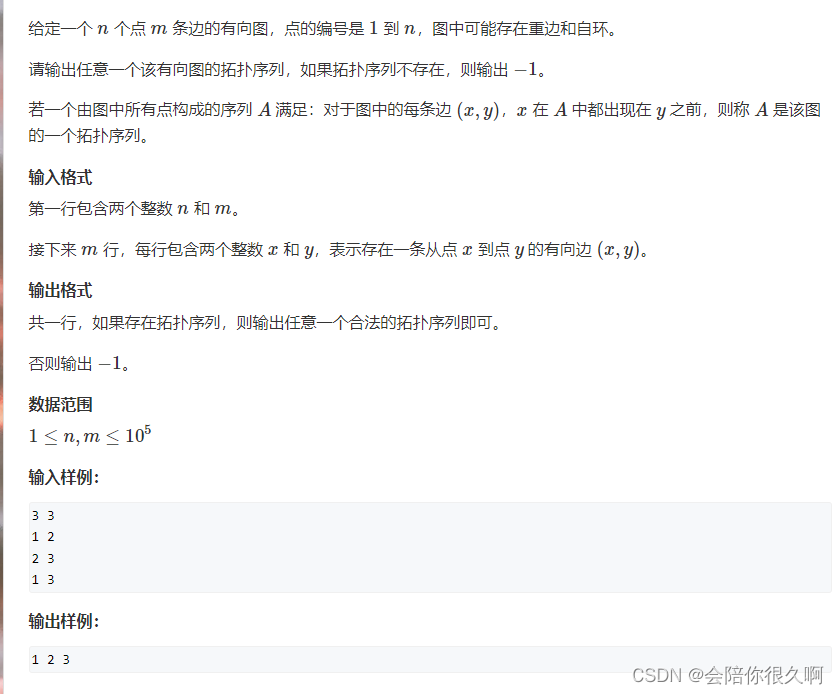
Acwing 848. 有向图的拓扑序列
#include
#include
#include
#include
using namespace std;
const int N = 1e5 + 10;
int e[N],ne[N],h[N],idx,d[N],n,m,top[N],cnt = 1;
// e,ne,h,idx 邻接表模板
// d 代表每个元素的入度
// top是拓扑排序的序列,cnt代表top中有多少个元素
void add(int a,int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++;
}
bool topsort(){
queue q;
int t;
for(int i = 1;i <= n; ++i)// 将所有入度为0的点加入队列
if(d[i] == 0) q.push(i);
while(q.size()){
t = q.front();//每次取出队列的首部
top[cnt] = t;//加入到 拓扑序列中
cnt ++; // 序列中的元素 ++
q.pop();
for(int i = h[t];i != -1; i = ne[i]){
// 遍历 t 点的出边
int j = e[i];
d[j] --;// j 的入度 –
if(d[j] == 0) q.push(j); //如果 j 入度为0,加入队列当中
}
}
if(cnt < n) return 0;
else return 1;
}
int main(){
int a,b;
cin >> n >> m;
memset(h,-1,sizeof h);
while(m–){
cin >> a >> b;
add(a,b);
d[b] ++;// a -> b , b的入度++
}
if(topsort() == 0) cout << “-1”;
else {
for(int i = 1;i <= n; ++i){
cout << top[i] <<" ";
}
}
return 0;
}
最后
以上就是魁梧棉花糖最近收集整理的关于拓扑排序算法的实现的全部内容,更多相关拓扑排序算法内容请搜索靠谱客的其他文章。
![[RoCE]网络QoS总结](https://www.shuijiaxian.com/files_image/reation/bcimg5.png)







发表评论 取消回复