matlab 数字信号处理（4）用FFT进行谱分析

124 阅读 0 评论 82 点赞

我是靠谱客的博主灵巧项链，最近开发中收集的这篇文章主要介绍matlab 数字信号处理（4）用FFT进行谱分析，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

实验四用 FFT 进行谱分析

一、实验目的

1. 加深对 FFT 算法原理的理解（因为 FFT 只是 DFT 的一种快速算法，所以 FFT 的运算结果必然满足 DFT 的基本性质）。

2. 熟悉 FFT 子程序的应用。

3. 用 FFT 对连续信号和时域离散信号（如语音和图像信号）进行谱分析的实现方法，能理解可能出现的分析误差，能分析误差的原因，以便在实际应用中能正确使用 FFT 。

4. 对同一信号，可分别在时域和频域中进行表示或描述，以便从不同域，也就是不同的角度对信号进行特性分析，或进行有效处理，因此要建立从多种角度看待问题的哲学思想和科学思维。

二

应当注意，如果给出的是连续信号，则首先要根据其最高频率确定采样频率 fs 以及由频率分辨率选择采样点数 N ，然后对其进行软件采样（即计算 x ( n ) = x a ( nT ),(0 < n < N − 1) ），产生对应序列。对信号 x 6 ( t ) ，频率分辨率的选择要以能分辨开其中的三个频率对应的谱线为准则。对周期列，最好截取周期的整数倍进行谱分析，否则有可能产生较大的分析误差。请实验者根据 DFT 的隐含周期性思考这个问题。

三、函数介绍

Matlab 中常用的快速傅里叶变换函数

1 、 Y=fft(x,N)

采用 FFT 算法计算序列向量 x 的 N 点 DFT ，这里假设 x 的长度为 R 。

（ 1 ）当省略 N 时， fft 函数计算 x 的 R 点的 DFT ， Y 的长度也为 R ；

(2 ）若 R>N ，截取 x 的前 N 点计算 DFT ， Y 的长度为 N ；

(3 ）若 R<N ，对 x 先补零扩展为 N 点长序列，再求 N 点 DFT ， Y 的长度为 N 。

2 、 x=ifft(Y,N)

采用 FFT 算法计算序列向量 Y 的 N 点 IDFT 。

3 、 Y=fft2(x,M,N) % 二维快速离散傅里叶变换

（ 1 ）当省略 M 和 N 时，计算 x 二维离散傅里叶变换, Y 的长度与 x 相同；

(2 ）对 x 进行截断或补零扩展，以便在计算变换之前 x 形成 m × n 矩阵,计算得到的 Y 是 m × n 矩阵。

4 、 Y=fftshift(X) % 将零频率的分量移到频谱的中心

四、实验内容

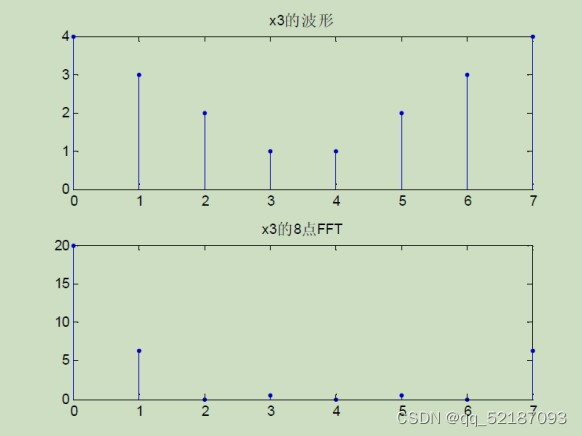
【实例 4-1】对 x3 做 8 点 FFT，绘制出离散幅度谱。

Matlab 参考代码如下：

N=8;

x=[4:-1:1 1:4];

x a ( t )

x ( n ) xk=fft(x,N);

figure;

subplot(211); stem(0:length(x)-1,x,’.’);

title(‘x3 的波形 ’) ；

subplot(212);

stem(0:N-1,abs(xk),’.’);

title(‘x3 的 8 点离散幅度谱 ’) ；

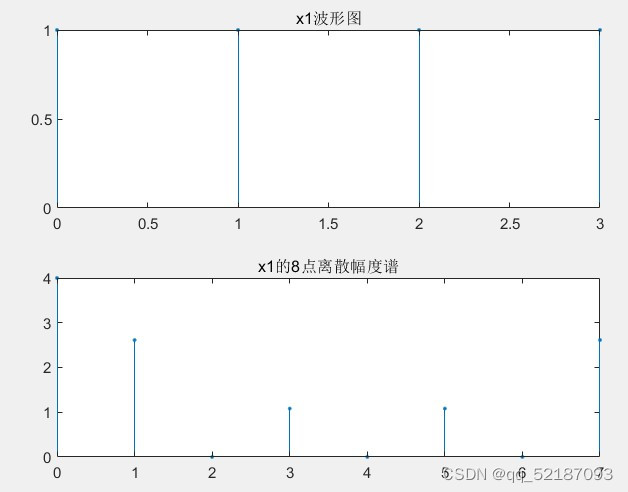
1.编写 Matlab M 文件对信号 x1 (n) 做 8 点和 16 点的 FFT

%1
x1=[1 1 1 1];
N1=8;
N2=16;

figure(1);
subplot(2,1,1);
stem(0:3,x1,'.')
title('x1波形图');
subplot(2,1,2);
xk1=fft(x1,N1);
stem(0:N1-1,abs(xk1),'.');
title('x1的8点离散幅度谱');

figure(2);
subplot(2,1,1);
stem(0:3,x1,'.');
title('x1波形图');
subplot(2,1,2);
xk2=fft(x1,N2);
stem(0:N2-1,abs(xk2),'.');
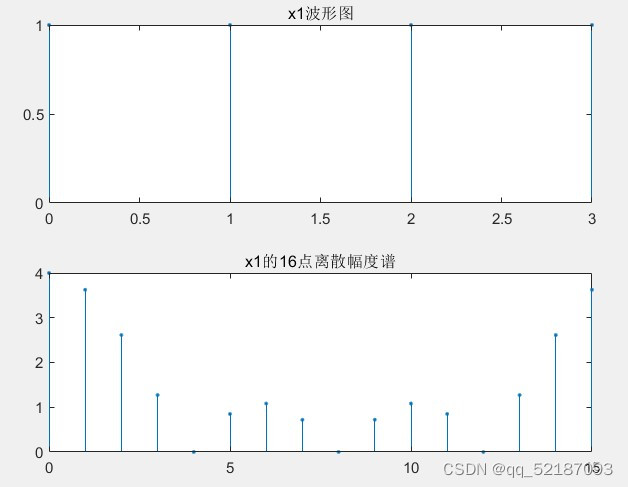
title('x1的16点离散幅度谱');

2 、编写 Matlab M 文件对信号x2(n)做 8 点和 16 点的 FFT

%2
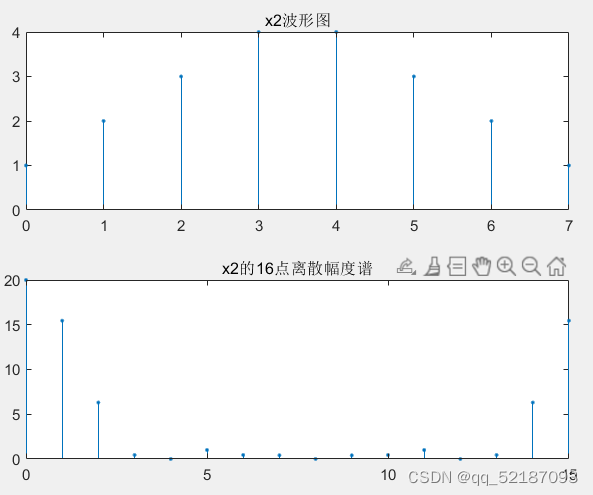
x2=[1:4 4:-1:1];
N1=8;
N2=16;

figure(1);
subplot(2,1,1);
stem(0:7,x2,'.')
title('x2波形图');
subplot(2,1,2);
xk1=fft(x2,N1);
stem(0:N1-1,abs(xk1),'.');
title('x2的8点离散幅度谱');

figure(2);
subplot(2,1,1);
stem(0:7,x2,'.');
title('x2波形图');
subplot(2,1,2);
xk2=fft(x2,N2);
stem(0:N2-1,abs(xk2),'.');
title('x2的16点离散幅度谱');

3 、编写 Matlab M 文件对信号 x4(n)做 8 点和 16 点的 FFT

%3
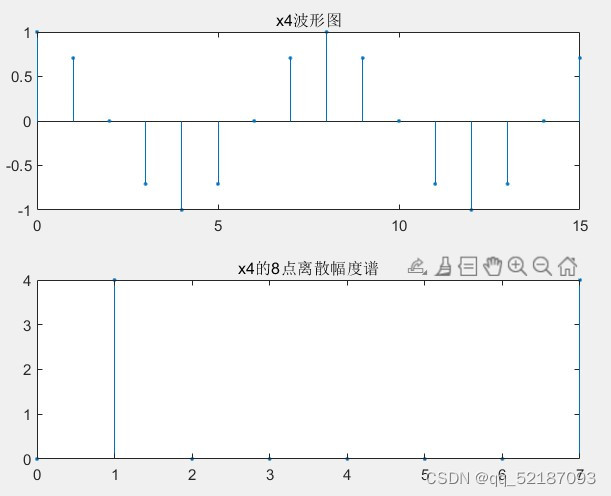
n=0:15;
x4=cos(pi/4.*n);
N1=8;
N2=16;

figure(1);
subplot(2,1,1);
stem(n,x4,'.')
title('x2波形图');
subplot(2,1,2);
xk1=fft(x4,N1);
stem(0:N1-1,abs(xk1),'.');
title('x2的8点离散幅度谱');

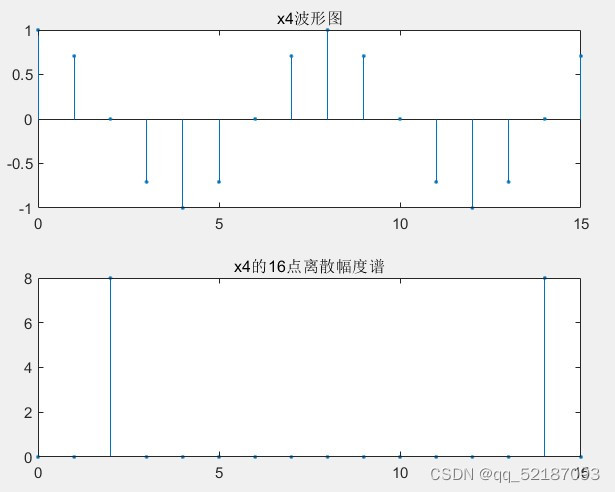
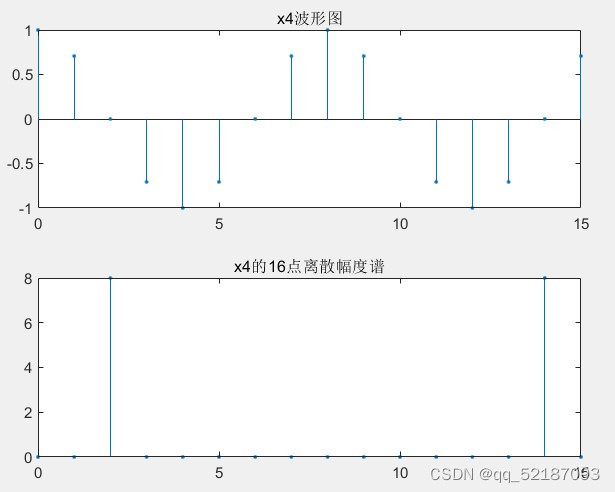
figure(2);
subplot(2,1,1);
stem(n,x4,'.');
title('x2波形图');
subplot(2,1,2);
xk2=fft(x4,N2);
stem(0:N2-1,abs(xk2),'.');
title('x2的16点离散幅度谱');

4 、编写 Matlab M 文件对信号 x6(t)以 fs=64 （ Hz ）采样后做 N=16 、 32 、 64 点的FFT

%4 时域周期频域离散时域非周期频域连续连续无法处理故截取时要整数倍周期
fs=64;
T = 1/fs;
N1 = 16;
N2 = 32;
N3 = 64;
n = 0:39;
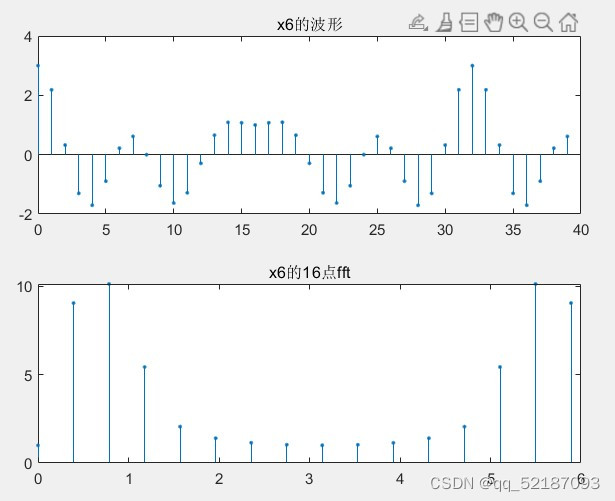
x6= cos(8*pi.*n*T)+cos(16*pi.*n*T)+cos(20*pi.*n*T);

figure(1);
subplot(2,1,1);
stem(n,x6,'.');
title('x6的波形');
subplot(2,1,2);
xk1 = fft(x6,N1);
stem(0:2*pi/N1:2*pi-2*pi/N1,abs(xk1),'.');

%这里横坐标采用w 通过DTFT 和 DFT公式可以推出两者间的关系
title('x6的16点fft');

figure(2);
subplot(2,1,1);
stem(n,x6,'.');
title('x6的波形');
subplot(2,1,2);
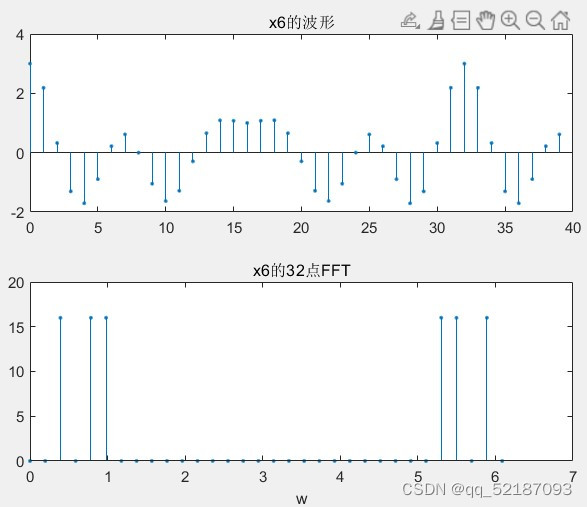
xk2 = fft(x6,N2);
stem(0:2*pi/N2:2*pi-2*pi/N2,abs(xk2),'.');
title('x6的32点FFT');
xlabel('w');

figure(3);
subplot(2,1,1);
stem(n,x6,'.');
title('x6的波形');
subplot(2,1,2);
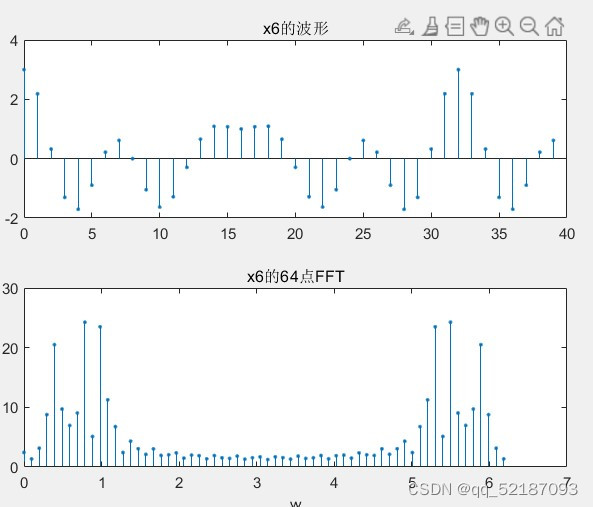
xk3 = fft(x6,N3);
stem(0:2*pi/N3:2*pi-2*pi/N3,abs(xk3),'.');
title('x6的64点FFT');
xlabel('w');

5 、编写 Matlab M 文件，读取 motherland.wav 音频数据，分析第 8000 至 8199 共 200 个采样点的频谱（提示这里的频谱指的是信号的傅里叶变换）。实现方法为：对这 200 个点数据做 N=512 的 DFT （采用 FFT 实现）。要求：画出其在 [0,2 π ) 的连续幅度谱和相位谱图。

clear;
clc;

[xn, fs] = audioread('motherland.wav');
x = xn(8000:8199,1);
N = 512;
xk = fft(x,N);

figure(1)
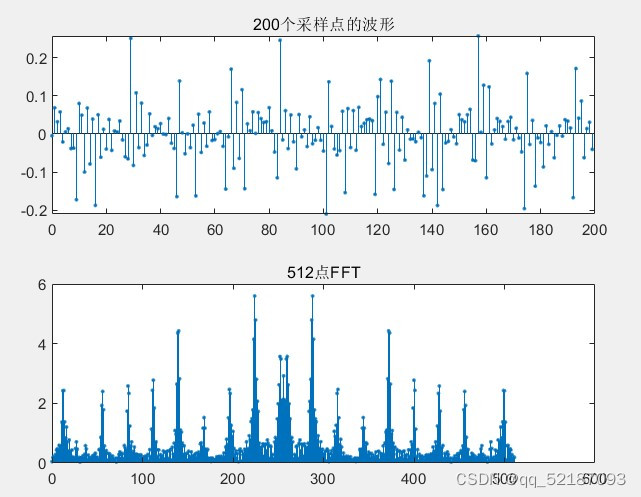
subplot(2,1,1);
stem(0:199,x,'.');
title('200个采样点的波形');
subplot(2,1,2);
stem(0:N-1,abs(xk),'.');
title('512点FFT');

figure(2)
h1 = abs(xk);
h2= angle(xk);
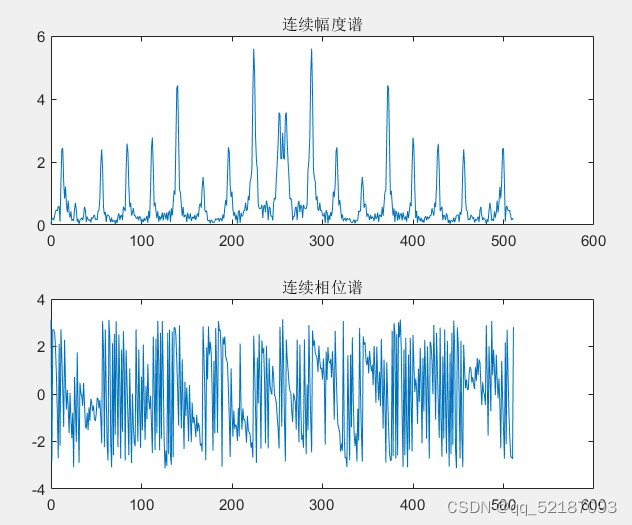
subplot(2,1,1);
plot(0:N-1,h1);
title('连续幅度谱');
subplot(2,1,2);
plot(0:N-1,h2);
title('连续相位谱');

6 、编写 Matlab 程序，分析 lena 图像的二维频谱，调用 fft2 和 fftshift 函数实现。要求：显示时域原图、二维幅度谱图。

A = imread('lena.bmp'); % 读原图
figure(1);
imshow(A);
title('原图')
fftI = fft2(A); % 二维离散傅里叶变换
A1 = abs(fftI); % 取模值
% 把幅度限定在[0,255]
B1=(A1-min(min(A1)))/(max(max(A1))-min(min(A1)))*255;
figure(2)
imshow(B1); title('二维幅度谱图');
B= fftshift(B1);
figure(3)
imshow(B);
title('移到中心位置的二维频谱图');